基于遗传算法和正则化极限学习机的PM2.5浓度预测研究

PM_2.5 Prediction Based on Genetic Algorithm and Regularized Extreme Learning Machine

摘要: 环境质量与人们的健康息息相关，一直是研究的热点。本文选取长沙市2017年NO₂、PM₁₀等大气数据对PM_2.5日均值进行预测，采用BIC准则进行特征选择。在传统的超限学习机(ELM)的基础上，引入正则化项以控制模型的复杂度，并用遗传算法(GA)对模型的输入层权重矩阵和隐含层阈值矩阵进行优化，建立遗传算法和正则化极限学习机(GA-RE-ELM)的PM_2.5预测模型。实验表明，该模型相比BP神经网络、超限学习机有更好的精度，均方误差分别降低了35.09%、25.49%，平均绝对误差分别降低了40.86%、30.80%，平均绝对百分误差分别降低了45.49%、31.65%，为PM_2.5浓度的预测提供一种新的方法。

Abstract: Environmental quality is closely related to people’s health and has always been a research hotspot. In this paper, the daily average values of PM_2.5 are predicted by atmospheric data such as NO₂ and PM₁₀ in Changsha City in 2017, and the BIC criterion is used for feature selection. On the basis of the traditional over-limit learning machine (ELM), the regularization term is introduced to control the complexity of the model, and the input layer weight matrix and the hidden layer threshold matrix of the model are optimized by genetic algorithm (GA) to establish the genetic algorithm. Then the PM_2.5 prediction model of the regularized limit learning machine (GA-RE-ELM) is built, the experiment shows that the model achieves more state of the art performance than the BP neural network and the over-limit learning machine, the mean square error is reduced by 35.09% and 25.49%, the average absolute error is reduced by 40.86% and 30.80%, and the average absolute percentage error is reduced by 45.49% and 31.65%. Meanwhile, it provides a new method for predicting PM_2.5 concentration.

1. 引言

空气质量的好坏和人们的健康息息相关，PM_2.5作为衡量空气质量的重要标准，逐渐引起人们的重视，进而成为众多学者研究的热点 [1] 。从国内外近几年的研究状况来看 [2] ，应用数值方法来预测PM_2.5浓度通常需要较详细的排放源时空分布资料和高分辨率的气象模式，但该方法的发展在我国的大部分城市并不成熟 [3] 。而回归分析 [4] 、时间序列 [5] 、贝叶斯网络 [6] 等广泛应用的空气质量统计预测方法，其预测精度并不能令人满意 [7] 。随着计算机技术和理论的发展，基于智能原理的人工神经网络、支持向量机模型在PM_2.5浓度的预测中取得了不错的效果 [8] 。然而，传统的神经网络容易过拟合，隐藏层神经元个数难以确定、寻找结构参数复杂，而且在输入数据较多且具有多重共线性时 [2] ，神经网络模型的训练效率会降低，从而影响空气质量预测的精度。陈绍炜 [9] ，易少强 [10] ，张卫辉 [11] 等分别提出了各种与极限学习机(ELM)结合的预测模型，在工程问题上取得了一定的效果 [12] ，但这些方法都有可能陷入局部最优。

本文运用BIC信息准则选择与PM_2.5浓度相关的指标，并结合遗传算法和正则化项，提出了一种基于超限学习机的PM_2.5预测模型(GA-RELM)。该预测模型融合了遗传算法全局寻优和正则化项能控制ELM模型复杂度，能有效地提高PM_2.5浓度预测的精度，并分析与其有关的指标，为加强环境污染的防控提供有力的参考。

2. 研究方法

2.1. BP神经网络

误差反向传播算法(BP)解决的了神经网络隐含层连接权值的问题，进而解放了BP神经网络的应用，它是至今为止最经典且最成功的学习算法之一。在实际任务中使用神经网络时，大多是用BP算法进行训练 [13] 。1989年Robert Hecht-Nielsen提出了万能逼近定理：具有输出层和至少一层具有激活函数的隐藏层，只要给予足够数量的隐藏层神经元 [14] ，那么它可以任意精度地毕竟一个闭区间内的连续函数 [15] 。

2.2. 传统的极限学习机

单隐藏层神经网络是十分常用的网络结构，广泛地运用于各种分类、预测问题上。但其梯度下降学习算法效率较低且容易造成过拟合。黄广斌 [16] [17] 等人提出超限学习机模型，通过对隐层神经元阈值和输入层、隐藏层的连接权重的随机赋值，通过Moore-Penrose广义逆求解出输出权重，最终得到唯一的最优解 [18] 。

2.3. 遗传算法和正则化极限学习机算法

通过增加正则化项以惩罚系数 $\beta$ ，进而得到更好的泛化性能 [16] [17] 。则超限学习机的目标函数为：

$\begin{array}{l}\underset{\beta \in R^{L\times m}}{\min }\frac{1}{2}{\Vert \beta \Vert }^2+\frac{C}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert e_i\Vert }^2}\\ \text{s}\text{.t}h\left(x_i\right)\beta =t_i^{\text{T}}-e_i^{\text{T}},i=1,\cdots ,N\end{array}$ (1)

其中,第一项为正则化项，可控制预测模型的复杂程度。将约束条件带入其目标函数中，我们即得到下面的等价的无约束优化问题：

$\underset{\beta \in R^{L\times m}}{\min }{L}_{ELM}=\frac{1}{2}{\Vert \beta \Vert }^2+\frac{C}{2}{\Vert T-H\beta \Vert }^2$ (2)

可将上面的问题称为岭回归或者正则化最小二乘法，通过将 $L_{ELM}$ 对 $\beta$ 求导并令其等于零，我们可以得到：

$L_{ELM}={\beta }^{*}-C{H}^{\text{T}}\left(T-H{\beta }^{*}\right)=0$ (3)

对训练集的数量(N)和隐层神经数量(L)的不同，我们可以得到 $\beta$ 的两种不同近似解：

$\beta =\{\begin{array}{l}{H}^{\text{T}}{\left(\frac{I}{C}+H^{\text{T}}H\right)}^{-1}T\text{if}N\le L\\ {\left(\frac{I}{C}+H^{\text{T}}H\right)}^{-1}{H}^{\text{T}}T\text{if}N>L\end{array}$ (4)

其中，I是纬度为L的单位矩阵。

遗传算法 [19] (Genetic Algorithm, GA)是一种基于概率转换的计算方法，是全局搜索的运算模型。它可以将PM_2.5浓度预测模型的解看成种群，再通过各种遗传学上的操作，让问题解的精度越来越来。

因此，本文提出了一种结合遗传算法和正则化项的超限学习机(GA-RELM)的PM_2.5浓度预测模型，该算法增加了正则化项，用于控制空气质量预测模型的复杂性。并通过遗传算法全局搜索寻优的能力，计算正则化极限学习机(RE-ELM)学习模型最优的隐藏层阈值和输入层、隐藏层的连接权值，进而提高PM_2.5浓度预测模型的泛化能力。该学习模型融合了遗传算法和正则化项的优点，对传统ELM随机产生输入层权值矩阵和隐含层阈值矩阵所造成网络预测出的PM_2.5浓度值变化较大的问题，是有效的解决方法，在控制学习模型复杂性的同时，还能增加其泛化性能。

在该学习模型中，将RE-ELM训练样本的输入层、隐藏层的连接权值和隐含层神经元的阈值，看成遗传算法生物中染色体的基因；染色体的适应度即RE-ELM训练样本的均方误差，如此便可以把学习模型中最优的连接权值、阈值的求解问题转化为以降低染色体适应度为目的，选择最佳的染色体问题。总之，结合了遗传算法和正则化项的超限学习机的学习模型，融合了遗传算法的全局搜索最优的能力和RE-ELM的强大学习及泛化性能。

本文将实验样本(PM_2.5浓度及其各种影响因素)划分为训练集和验证集两个部分，同时为了减少因为样本数据数量级的差距导致的误差，本文对PM_2.5浓度预测模型的相关数据做了归一化处理。 [20] 首先初始化种群，每个染色体中都包含输入层、隐藏层之间的连接权值和隐藏层的阈值；接着采用遗传算法寻找RE-ELM学习模型最佳的初始权值和阈值，本文使用训练集预测误差的均方误差作为个体适应度函数；最后，用GA计算得到的最佳权值和阈值对正则化超限学习机模型的初始连接权值和阈值进行复制，同时设定隐藏层神经元的数量，至此建立了GA-RELM空气质量预测模型；最后利用测试集样本对GA-RELM模型进行测试及效果评价。

3. 基于遗传算法和正则化极限学习机的PM_2.5浓度预测

本文采用GA-RELM学习模型对长沙市2017年的PM_2.5浓度进行预测，算法的具体过程如图1。

3.1. 数据来源

长沙市是我国长江中游地区最重要的城市之一，长沙冬天寒冷且干燥，夏天炎热少雨，汽车、工业排放量较大，只是空气质量不佳。从图2的原始PM_2.5浓度的数据可以看出，浓度呈现非线性的特征。

本文选取长沙市2017年空气质量数据来预测PM_2.5浓度。其中所使用的空气质量数据(包括SO₂、NO₂、PM₁₀、CO、O₃)来自长沙市环境监测站，资料取2017-01-01至2017-12-31共365天的日均值数据。所采用的实时气象数据有最高气温(T_max)、最低气温(T_min)、平均气温(T_avg)，均来自长沙市气象局。并选取后40天的样本数据作为测试集，其余的样本数据作为模型的训练样本。

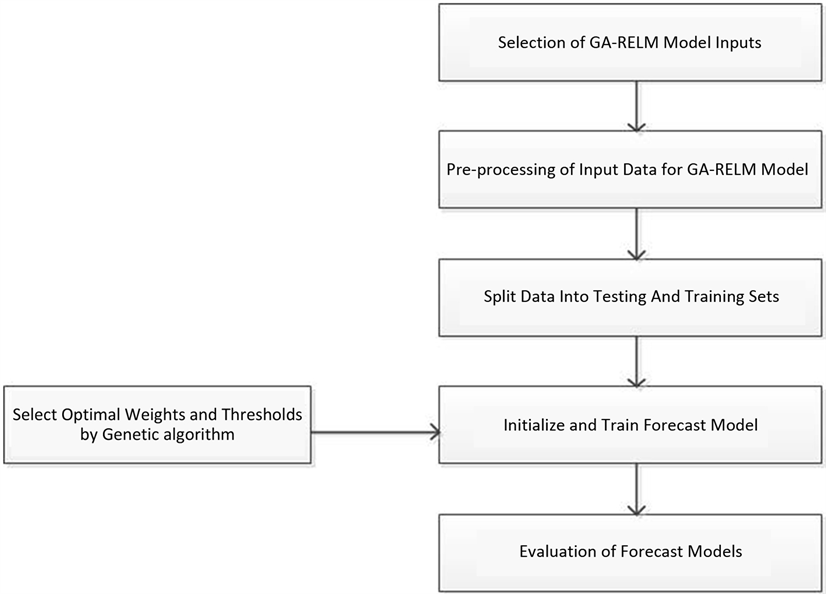
Figure 1. GA-RELM based forecast framework steps

图1. 基于GA-RELM的预测框架

Figure 2. Changsha City 2017 PM_2.5 concentration raw data

图2. 长沙市2017年PM_2.5浓度原始数据

3.2. 预测精度评价指标

1)平均绝对误差

$MAE=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left|R_{pred}-R_{obs}\right|}$ (5)

2)相对百分误差绝对值的平均值

$MAPE=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left|\frac{R_{pred}-R_{obs}}{R_{obs}}\right|}$ (6)

3)均方根误差

$RMSE=\sqrt{\frac{1}{N}{\displaystyle {\sum }_i^N{\left(R_{pred}-R_{obs}\right)}^2}}$ (7)

式中， $R_{obs}$ 、 $R_{pred}$ 分别为真实值和预测值,N为测试集样本数。

3.3. 算法过程

3.3.1. BIC准则进行PM_2.5浓度相关特征的提取

在预测问题上，模型变量的选择是至关重要的，对预测模型的精度有很大的影响。本文采用贝叶斯贝叶斯信息准则(BIC)对PM_2.5浓度预测模型进行变量选择，BIC准则的基本思想是假设候选模型中存在均匀分布，接着在学习模型上找到后验分布，最后选择具有最大后验概率的模型，因此我们认为最小化BIC值的变量子集是最优的 [21] 。

$\text{BIC}=-2\ln g\left({\hat{\theta }}_k|y\right)+k\log n$ (8)

表1显示了不同模型大小的最佳预测子集的输出，本文选择了关于PM_2.5浓度的8个变量(前一日的SO₂、NO₂、PM₁₀、CO、O₃、T_max、T_min、T_avg)，因此输出最优的8个变量模型。从表2可以看出，第5

个模型的BIC值最低，所以我们选择与该模型对应的变量子集作为后续学习模型的变量，它们分别为前一日的NO₂、PM₁₀、CO、Tmax和Tavg，以第二天的PM_2.5浓度日均值作为输出。

3.3.2. 模型参数的设置

通过上述分析，我们最终选取2017-01-01至2017-11-21的325组数据作为训练样本，2017-11-21至2017-12-30的40组数据作为测试集。并以长沙市前一日的NO₂、PM₁₀、CO、T_max和T_avg值作为预测模型的输入，第二天的PM_2.5浓度值作为输出。

在以下的实验中，将预测模型的输入数据都归一化到[0, 1]之间，隐藏层的激活函数均使用Sigmoid。而GA-RELM的PM_2.5浓度预测模型的参数，经过多次测试调整，推荐值见表3。

在单隐层前馈神经网络模型中，隐藏层神经元的数目大小十分关键，超限学习机作为单隐层前馈神经网络模型之一也是如此。神经元数目过多容易造成模型的过拟合，而数目太少会出现欠拟合的情况，都将降低PM_2.5浓度的预测效果。因此，本文通过不断试验和改变网络的隐层节点数目，寻找较优的节点

Table 1. Subsets of optimal predictor variables for different model sizes

表1. 不同模型大小的最佳预测变量子集

Table 2. BIC values for different variable subsets

表2. 不同变量子集模型的BIC值

Table 3. GA-RE-ELM parameters setting table

表3. GA-RE-ELM参数表

数。选取ELM网络隐含层节点数范围为[1,200]，计算相应测试集样本均方误差的大小，其结果如图3所示。

从图3表明，网络隐层神经元数量的增加，会导致测试样本的均方误差在整体上呈现出先降低后升高的趋势，符合前文的分析。为了更精确地选出较优的隐层节点数，本文选取图3中均方误差较低的几个点，对不同的隐层神经元数量的模型进行100次试验，并记录下测试样本均方误差的均值，如表4所示。

由表4可得，隐藏层神经元数量为43时，学习模型在测试集上的均方误差是最低的。为了便于评价模型的优劣，本文令BP神经网络、ELM神经网络、GA-RELM模型中的隐藏层神经网络数目均为43。

3.3.3. 实验结果与分析

把表3的值作为GA-RELM预测模型的参数，对长沙市PM_2.5浓度进行预测。通过图4 GA优化的进化过程，可以看出GA-RE-ELM预测模型经过150次的计算能得到一个最佳的适应度的稳定迭代值。

为了更好地验证所提出模型的预测效果，本文分别运用BP神经网络、传统的ELM模型对长沙市PM_2.5的浓度进行预测，训练样本和测试样本的划分一致。从图5三种预测模型预测结果的绝对误差曲线可以看出，GA-RELM预测模型的绝对误差曲线相对其它两个模型最为平稳，且大部分预测值的绝对误差在10 ug/m³之内，在可接受的范围之内。从图6的各个模型的PM_2.5浓度预测曲线可以看出，GA-RELM的预测效果是最佳的，ELM预测模型次之。

表5列明了这三种预测模型在训练样本和测试样本上的预测结果，由表中数据分析可知：GA-RELM模型在长沙市PM_2.5浓度的预测中取得了最优的效果。不管是训练集还是测试集，GA-RELM均取得了最

Figure 3. Testing process of hidden layer number

图3. 网络的隐层节点数试验过程

Table 4. Comparison of repeated test results

表4. 多次重复实验结果比较

好的预测精度，且具有很强的泛化能力。在测试集上，GA-RELM的均方误差BP神经网络和ELM分别降低了35.09%、25.49%，平均绝对误差分别降低了40.86%、30.80%，平均绝对百分误差分别降低了45.49%、31.65%。

4. 结论

PM_2.5浓度预测的准确可以为有效地治理空气污染发挥重要的作用。但是，PM_2.5成因复杂、其浓

Figure 4. Error evolution curve of GA

图4. 遗传算法优化的进化过程

Figure 5. Absolute error of prediction results of three models

图5. 三种模型预测结果的绝对误差

Figure 6. Comparisons between predicted results of GA-RE-ELM model and the true values of test data

图6. 三种模型对测试集样本的预测结果与测试集真实值对比

Table 5. Comparisons of prediction consequences for the different models

表5. 不同模型预测的预测结果对比

Note: Tra means Traing.

度数据呈现非线性和不规律等特点增大了准确预测PM_2.5浓度的难度。所以，有效地预测PM_2.5浓度的模型方法是十分有必要研究的。正如前言所说，运用数值方法来预测PM_2.5目前在我国的大部分地区并不成熟 [2] [3] ，而回归分析 [4] 、时间序列 [5] 的预测精度往往不能让人满意。运用基于智能原理的神经网络等方法将成为一个趋势，而传统的神经网络存在过拟合、结构参数寻找复杂等不足，针对这些不足，ELM应运而生 [12] 。

然而，传统的超限学习机(ELM)模型由于随机产生输入连接权值和隐层神经元的阈值，会造成预测结果不稳定，本文运用BIC信息准则选择与PM_2.5浓度相关的指标，并将遗传算法、正则化与极限学习机相结合，提出了一种GA-RE-ELM模型，将其应用于长沙市PM_2.5浓度的预测中。在该算法中，正则化项能控制学习模型的复杂度，遗传算法能对预测模型的输入层权值和隐含层阈值矩阵进行优化，从而降低了其随机性对结果的影响，能得到更好的预测效果，丰富了PM_2.5浓度的预测方法，具有很好的实际运用价值。

基金项目

本研究由国家自然科学基金资助，资助项目61375063，61773404，11301549和11271378，部分资金由中南大学研究生创新基金会(2018zzts322)资助。

参考文献

NOTES

*通讯作者