1. 引言
目前,无线通信网络的工作时长受设备能量的制约,在这一背景下,无线能量收集技术受到了广泛的关注与研究 [1] ,并已被证明可有效运用于无线网络中,延长设备的使用时间 [2] [3] [4] ,由于射频信号可以同时承载信息与能量,参考文献 [5] [6] [7] [8] [9] 研究了无线信息与能量同时传输系统(SWIPT),为后续的理论研究奠定了基础。
无线能量收集技术可以一定程度上解决无线网络的能源短缺问题,但随着网络中接入的设备不断增多,用户的可用频谱受到了极大的限制。与此同时,在偏远地区,信号覆盖也是一个问题。为了解决这一困境,随着多输入多输出(MIMO)技术的成熟,学者们证明了运用MIMO技术可以有效提高数据吞吐量和系统信息传输距离,而无需额外的带宽或更高的能耗 [10] 。
MIMO无线传播信道的两个基本特征是广播和多路访问。因此,某个链路上的发送信号可以被无线网络中的其他相邻节点检测到。这些节点可以形成无线自组织(Ad Hoc)网络,并且作为接收终端的中继站来帮助转发消息。SWIPT MIMO与中继的结合可以有效提高系统传输速率,此时,无线网络的通信质量由射频能量接收机的结构和预编码性能决定。
在上述问题的驱动下,本文研究了包含两个用户的无线Ad Hoc网络(WAHN)中的MIMO系统。本文应用解码–转发(DF)协议下的功率分配接收机来研究发射信号的波束成形和中继节点的功率分配。设计目标是在满足主用户的通信速率需求的前提下,同时最优化功率分配和预编码设计,以最大化从用户的传输速率。此外,由于最优化算法带来的计算复杂度,本文分别利用奇异值分解(SVD)算法和块对角化(BD)算法给出了两个次优的预编码设计,用以与最优化方案作性能对比。
2. 系统模型
本文设计的具有中继节点的MIMO-WAHN网络如图1所示。系统包括源端节点S,机会主义中继节点R和两个终端节点——主用户i与从用户j。假设系统采用半双工模式进行传输,中继节点遵循DF协议进行数据转发,且所有的信道都是准静态平坦衰弱信道,源端节点配有M根发射天线。中继节点无固定电源且配有M根天线,这些天线同时用于发射源端节点及中继节点自身的信号,用户终端都配备有N根接收天线。中继节点转发源端节点的信息给主用户i的速率要求大于一个最低阈值以保证通信质量,在这一基础上,中继节点利用剩余的能量将自身的信息发送给从用户j。
在本系统中,传输分为两个时隙阶段完成。在第一个时隙,源端节点向中继节点同时发送能量和信
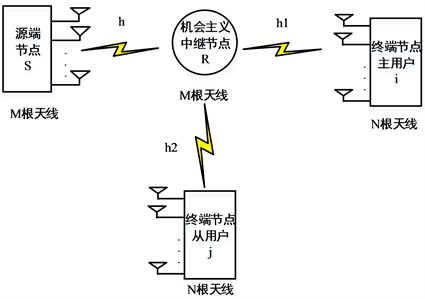
Figure 1. MU-MIMO model of wireless self organizing network system
图1. MU-MIMO无线自组织网络系统模型
息。传输信号为
,假设信道状态已知,且信道矩阵为
,中继节点不需要将信号从频带转换至基带来收集能量,中继节点接收到的信号可以表示为:
(1)
其中z表示源端节点至中继节点之间的加性高斯白噪声(AWGN)矢量,z相互独立且服从
,x的协方差矩阵被表示为
,源端节点的功率受
约束,中继节点通过功率分配的方式对所接收到的能量信息进行分配,分配系数为
的部分功率用于对接受信息的译码,
分配系数为
的部分功率被用于处理能量收集,此时,第一时隙内源端节点至中继节点的信息传输速率可表示为:
(2)
中继节点所收集到的能量可表示为:
(3)
其中
,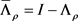 ,假设每根天线上的功率分配因子均相同,
,
,假设每根天线上的功率分配因子均相同,
,
在第一时隙中,满足中继节点信息接收速率的前提下,最大化中继节点收集到的能量,可以使得中继节点有充足的能量在第二时隙传输更多的信息,从而实现系统速率最大化。
第一时隙的中继节点能量收集最优化问题(P1)建模如下:
(4)
其中
表示源端节点的最低传输速率要求。
系统完成第一时隙的传输后,进入第二时隙阶段。此时中继节点通过解码转发(DF)协议,将自身所需传输的信号和从源端节点接收到的信号重新组合后同时传输给主用户和从用户,中继节点从源端节接受并解码的信号为
,中继节点自身所需传输的信号为
,此时在第二时隙内,主用户从中继节点接收到的信号矢量可被表示为:
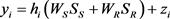 (5)
(5)
从用户从中继节点接收到的信号矢量为:
(6)
其中
,
分别表示中继节点与主、从用户之间的信道系数。中继节点使用预编码矩阵
来转发源端节点S的信号给主用户,并且使用预解码矩阵
来发送其自己的信号给从用户,以此消除用户之间的共道干扰,主、从用户接收端的加性高斯白噪声服从分布
,
。
因此,主用户的SINR可以表示为:
(7)
从用户的SINR可以表示为:
(8)
由于中继节点遵循DF协议将源端节点的信号转发至主用户,因此,当第一时隙中继节点接收源端节点信号的速率R与第二时隙中继节点转发源端节点信息给主用户的速率
相等时,源端节点与主用户之间的速率达到理论上的最大值 [11] ,基于此,给出第二时隙的优化目标:满足主用户传输速率的基础上,最大化从用户的速率,且传输过程的能耗由中继节点在第一时隙中从源端节点处收集的能量所提供。
第二时隙中的从用户速率最优化问题(P2)建模如下:
(9)
其中
表示主用户所需的最小速率。
3. 最优化解法
在第一时隙中,优化问题P1的优化目标为一个典型的凹函数,且限定条件中的限定函数为凸函数,因此,P1可被视为一个经典的凸优化问题,在求解过程中,首先对
从0到1的范围内进行迭代取值,这样可以把P1变为只有一个未知变量
,同时将
锁定为
,此时优化问题P1可被表示为:
(10)
此时利用Matlab对
进行
一维搜索,并调用CVX工具箱求解出最优的预编码矩阵
,
对应的
即为P1所求的最优功率分配因子,至此最优化问题P1算法已给出。
接下来,给出P2的最优解法。
首先,定义
,
及
,通过半正定规划算法,先松弛掉“秩为一”
这个限定条件,将P2变形为:
(11)
如果P2-SDR的解为
和
且满足条件
和
,则
和
为P2-SDR的最优解,继而可对
和
进行特征值分解以求出最优的预编码矩阵
和
。但如果
和
不满足
和
这一限定条件,那么求出的预编码矩阵
和
只是最优预编码矩阵解的一个上边界,最优的预编码矩阵
和
还需要通过“秩一逼近”算法求出。
为了进一步求解P2-SDR,首先引入等效替代因子t,对P2-SDR进行Charnes-Cooper等效转换,此时优化问题被表述为:
(12)
其次,P2-SDR-Equ为一个满足斯莱特(Slater)条件的凸优化问题,且与P2-SDR的对偶间隙为0。证明问题P2-SDR与P2-SDR-Equ等价的步骤如下:
1) P2-SDR的所有可行解为(S,Q),其对应的问题P2-SDR-Equ解为
,可以看出两个问题有同样的目标值S与Q。
2) 问题P2-SDR-Equ对应的可行解为(S,Q,t),而P2-SDR中的可行解为(S/t,Q/t),两个问题的目标值相同,因此两个问题是等价的。
问题P2-SDR-Equ可以通过在Matlab调用CVX工具箱求出最优值 [12] [13] 。
由于之前我们松弛掉了“秩为一”这一条件,导致问题P2-SDR-Equ的最优解中存在着两个矢量变量,分别为
和
,但由于预编码矩阵的秩必须是大于1的整数,且本文研究的系统包含两个用户,
所以只有当
时,有
[14] 。本文系统中K = 1,表
示只有一个从用户。此时求解出的
和
即为问题P2-SDR-Equ的最优解,对应的
和
为P2的最优预编码矩阵。
4. 次优化解法
由于最优化算法的求解过程多次调用CVX工具箱,且多次迭代带来了巨大的计算复杂度,为了算法的现实可行性,本节中分别为两个时隙中设计了一种次优化解法,与最优化解法对比性能,方便在实践中酌情运用次优化方案。
4.1. 通过奇异值分解(SVD)设计第一时隙中次优化预编码矩阵
在第一时隙中,假设信道状态已知,源端节点通过预编码矩阵
将信号发送给中继节点,中继节点处接收的信号可以表示为:
(13)
中继节点遵循DF转发协议,接下来讨论在中继节点接收机处通过奇异值分解以解码源端信号。
首先对信道矩阵做奇异值分解
,根据酉矩阵的性质,设计预编码矩阵
。在中继节点的信号接收端使用均衡矩阵
以解码来自源端的信号,通过解码处理后,接收信号可以表示为:
(14)
接下来,通过功率分配因子
对中继节点的功率进行分配,
部分用于解码信号,
部分用于能量收集,则中继节点从源端节点处收集到的能量为:
(15)
其中
表示中继节点处的能量转换效率。中继节点利用
部分功率对源端信号进行译码处理后的信号表示为:
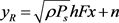 (16)
(16)
从源端节点到中继节点的信噪比为:
(17)
此时,第一时隙的优化问题P1-1可被描述为:
(18)
可以看出,P1-1的优化目标为最大化一个凹函数,且所有限定条件均为关于未知变量
的线性函数,由此可推出P1-1是一个凸优化问题,最优解可以通过KKT条件来求出。
令
分别是(18-2)和(18-3)的拉格朗日乘子,问题P1-1的KKT条件为:
(19)
(20)
(21)
(22)
P1-1的拉格朗日表达式
为:
(23)
由于
表示在第一时隙期间中继节点收获的能量,且
,只有当
且
时,KKT条件成立。对等式(23)求导后,有:
(24)
如果
,等式(24)转换为
,当且仅当
时成立,而这显然是没有意义的。因此可以排除。
如果
,有
,此时P1-1的解为:
。
综合考虑各种情况,这种情况是合理的,由此给出问题P1-1的最优解为
。
在本章节讨论的次优解方案中,第二时隙采用第二章节提出的波束赋形预编码最优解法,以对比性能。
4.2. 通过块对角化(BD)设计第二时隙中次优化预编码矩阵
在第二时隙中,中继节点对译码后的源端节点信号进行预编码处理,预编码矩阵为
,从用户j与中继节点之间的信道为
,对
其进行SVD分解,可得:
(25)
矩阵
,
分别由非零奇异值和零奇异值对应的右奇异向量组成,且有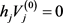 。即
是
的零空间。之后,对
进行SVD分解,可得:
。即
是
的零空间。之后,对
进行SVD分解,可得:
(26)
用矩阵
对中继节点转发给主用户i的源端节点信号进行预编码处理,可以使得从用户j无法接收此信号,从而达到干扰消除的目的。
同样的,可以设计出R自身需要发送给从用户j信号的预编码矩阵,此时对用户i的信道矩阵
进行SVD分解,可得:
(27)
信道矩阵
的零空间为
,对
进行SVD分解,可得:
(28)
此时,通过矩阵
对中继节点自身需要发送给从用户的信号进行预编码处理,可以使主用户屏蔽掉该信号,从而打扰消除干扰的效果。
接下来,通过对两类信号传输功率进行功率分配,讨论如何在保障主用户i传输速率的情况下,最
大化从用户j的速率。首先给出结合功率分流因数的预编码矩阵
,
,其中
,
,每个用户的每根天线的功率分配系数一致,有
和
,总发射功率限制为:
(29)
考虑在主用户的信号接收机处内置一个滤波矩阵
,此时,主用户i接收到的信号为:
(30)
主用户i的SINR为:
(31)
同样的,在从用户的信号接收机处内置一个滤波矩阵
,此时,从用户接收到的信号为:
(32)
从用户j的SINR为
(33)
可以给出第二时隙的次优化目标如下:
(34)
可以看出,该问题是一个典型的凸优化问题,通过调用Matlab中的CVX工具箱可以轻松求解,第二时隙的次优化算法于此描述完毕。
5. 仿真分析
在本章节中,通过Matlab仿真软件对本文设计的三种预编码方案进行性能对比。仿真环境设置如下:节点之间的传输信道经历平坦衰弱,且信道之间相互独立,不考虑大尺度衰弱,系统中主用户与从用户始终保持标准距离,中继节点处于源节点与主用户之间的直线距离中间位置。
当源端节点与终端节点的天线数目N = 4,主用户与从用户的天线数目M = 2时,仿真结果图2所示。
其中BF表示波束赋形最优化算法,SVD表示第一时隙中的奇异值分解次优化算法,BD表示第二时隙中的块对角化次优化算法,图中给出了三种优化方案下,主用户最低速率需求为
与
时的从用户速率。根据仿真所示,可以给出如下结论:
1) 主用户最低速率需求越大,从用户的总速率越小。这是因为中继节点在第一时隙中接收到的能量有限,主用户对速率的需求越高,中继节点可以分配给从用户的功率就越小,因此影响从用户的传输速率。
2) 通过波束赋形算法设计的最优化预编码矩阵在给定的两种情况下都表现出了最优性能。原因是波束赋形能够将发射信号的主瓣对应接收信号的到达角度,旁瓣对应干扰信号的到达角度,在能够增强有用信号的同时还能在一定程度上消除干扰信号,从而提高系统速率。但是最优化方案的实现复杂度很高,因此次优化解目前更具现实意义。
3) 在用户端的天线数量小于发射端天线数量时,块对角化预编码的效果与最优化方案非常接近,这是由于块对角化算法预编码可以将干扰信号映射到有效信号的零空间,从而达到干扰消除效果。块对角化算法预编码在用户数量较少,信道状态已知的条件下很容易实现预编码矩阵设计,计算复杂度较低。而采用奇异值分解算法进行预编码设计,会导致用户空间的子信道成90度,分解后子信道性能差异较大,因此效果相对较差。
源端节点、中继节点、主用户,从用户的天线数量相等,M = N = 4时,仿真结果如图3所示。
当各个终端天线数量相等时,可以看出:
1) 当用户端天线数量等于发射端时,块对角化算法的性能最差,这是因为随着天线数量的增多,信道维度变大,此时块对角化算法不能很好的消除用户间信道干扰,因此性能较差。

Figure 2. The system rate of the number of antennas at N = 4, M = 2
图2. 天线数量N = 4,M = 2时的系统速率
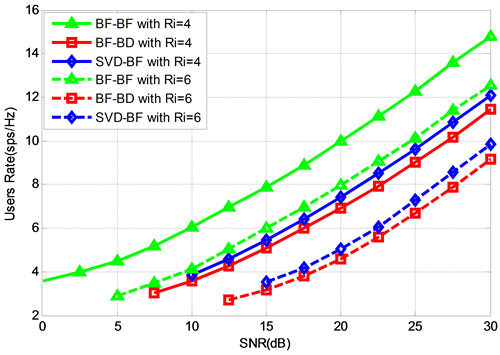
Figure 3. The system rate of the number of antennas at N = 4, M = 4
图3. 天线数量N = 4,M = 4时的系统速率
2) 用户端天线数量的增加显著地增强了系统的容量,最优化方案效果更佳明显。这是因为波束赋形算法不受分离的子信道性能及接收端天线数目的影响,且MIMO系统的吞吐量随天线数目增多而线性增长,因此波束赋形算法速率提升最大。
6. 结语
本文研究了基于能量收集的多用户MIMO无线自组织网络的预编码设计,通过波束赋形、奇异值分解和块对角化算法,分别为两个时隙设计了最优化及次优化的预编码方案,仿真结果表明,本文所设计的预编码方案能显著提高系统性能。