Hamilton矩阵广义逆的表示

The Representation of the Generalized Inverse of a Hamilton Matrix

摘要: 本文首先给出了Hamilton矩阵 在一定条件下Drazin逆 的表达式，其次给出了当广义Schur补 时Drazin逆 的表达式。

Abstract: The aim of this paper is to establish an explicit representation of the Drazin inverse of a Hamilton matrix under certain conditions. Then we give a formula for the Drazin inverse of a Hamilton matrix when the generalized Schur complement .

1. 引言

Hamilton体系是由19世纪爱尔兰数学家兼物理学家W. R. Hamilton从几何光学着手创建起来的理论模式，而后他将此模式创造性的应用于经典力学，得到了在经典力学范畴内的又一种力学描述形式—Hamilton力学 [1]。作为Hamilton系统中最简单且最基本的形式，有限维线性Hamilton系统所对应的系数矩阵如下：

$H=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)$ ,

其中 $B,C$ 是Hermite矩阵， $A^{*}$ 是A的共轭转置，此时称H是Hamilton矩阵 [2]。Hamilton矩阵作为一种特殊的分块矩阵，在数学以及力学的很多方面都有重要的作用，如谱的计算、Riccati方程的解以及相关的不变子空间刻画等 [3]。

设矩阵 $A\in C^{n\times n}$ ，A的Drazin逆是满足以下条件的唯一复矩阵 $A^D$ ：

$A^{D}A{A}^D=A^D$ , $A{A}^D=A^{D}A$ , $A^{k+1}{A}^D=A^k$ ,

其中k是使得 $rank\left(A^k\right)=rank\left(A^{k+1}\right)$ 成立的最小非负整数，记 $k=ind\left(A\right)$ 为A的指标 [4]。当 $ind\left(A\right)=1$ 时，则称 $A^D$ 为A的群逆。如果A是非奇异的，则 $ind\left(A\right)=0$ 且 $A^D=A^{-1}$ ，本文中令 $A^{\pi }=I-A{A}^D$ 。

Drazin逆在Markov链、奇异微分方程和差分方程、迭代方法等各领域起着重要作用 [5]。本文主要研究了Hamilton矩阵在一定条件下的Drazin逆，并给出了一些 $H^D$ 的表达式。

2. 引理

为了得到本文的主要结论，首先给出以下引理。

引理1 ( [6]). 令 $P,Q\in C^{n\times n}$ ，如果 $P^{2}Q=0,PQ+QP=0$ ，那么 ${\left(P+Q\right)}^D=P^D+\left(P+Q\right){\left(Q^D\right)}^2$ 。

引理2 ( [6]). 令 $P,Q\in C^{n\times n}$ ，如果 $P^{2}Q=0,Q{P}^{\pi }=0$ ，那么 ${\left(P+Q\right)}^D=P^D+Q{\left(P^D\right)}^2+PQ{\left(P^D\right)}^3$ 。

引理3 ( [7]). 令 $T\in C^{n\times n}$ ，如果 $T=\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right),B\in C^{p\times \left(n-p\right)},C\in C^{\left(n-p\right)\times p}$ ，则 $T^D=\left(\begin{array}{cc}0& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& 0\end{array}\right)$ 。

引理4 ( [8]). 令 $P,Q\in C^{n\times n}$ ，如果 $PQ=0$ ，P是l-幂零的，则 ${\left(P+Q\right)}^D={\displaystyle \underset{i=0}{\overset{l-1}{\sum }}{\left(Q^D\right)}^{i+1}{P}^i}$ 。

如果 $PQ=0$ ，Q是s-幂零的，则

${\left(P+Q\right)}^D={\displaystyle \underset{i=0}{\overset{s-1}{\sum }}{Q}^i{\left(P^D\right)}^{i+1}}$ .

引理5 ( [9]). 令 $M=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ , $A\in C^{m\times m}$ , $D\in C^{p\times p}$ 。若 $S=D-C{A}^{D}B=0$ , $A^{\pi }B=0$ , $C{A}^{\pi }=0$ ，则

$M^D=\left(\begin{array}{c}I\\ C{A}^D\end{array}\right){\left[{\left(AW\right)}^D\right]}^{2}A\left(\begin{array}{cc}I& A^{D}B\end{array}\right)$ , $W=A{A}^D+A^{D}BC{A}^D$ .

3. 主要结论及证明

定理1. 令 $H=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)$ ，其中A为方阵，如果 $A^{2}B=0$ , ${\left(A^{\ast }\right)}^{2}C=0$ , $-B{\left(A^{\ast }\right)}^{\pi }=0$ , $C{A}^{\pi }=0$ ，那么

$H^D=\left(\begin{array}{cc}{A}^D& B{\left({\left(A^{\ast }\right)}^D\right)}^2-AB{\left({\left(A^{\ast }\right)}^D\right)}^3\\ C{\left(A^D\right)}^2-A^{\ast }C{\left(A^D\right)}^3& -{\left(A^{\ast }\right)}^D\end{array}\right)$ .

证明：将矩阵H分解，得

$H=\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)\text{+}\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)$ ,

令

$P=\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)$ , $Q=\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)$ ,

通过条件我们得到

,

,

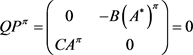因此，矩阵P和Q满足引理2，得到

$\begin{array}{c}{H}^D={\left(P+Q\right)}^D=P^D+Q{\left(P^D\right)}^2+PQ{\left(P^D\right)}^3\\ =\left(\begin{array}{cc}{A}^D& 0\\ 0& -{\left(A^{\ast }\right)}^D\end{array}\right)+\left(\begin{array}{cc}0& B{\left({\left(A^{\ast }\right)}^D\right)}^2\\ C{\left(A^D\right)}^2& 0\end{array}\right)+\left(\begin{array}{cc}0& -AB{\left({\left(A^{\ast }\right)}^D\right)}^3\\ -A^{\ast }C{\left(A^D\right)}^3& 0\end{array}\right)\\ =\left(\begin{array}{cc}{A}^D& B{\left({\left(A^{\ast }\right)}^D\right)}^2-AB{\left({\left(A^{\ast }\right)}^D\right)}^3\\ C{\left(A^D\right)}^2-A^{\ast }C{\left(A^D\right)}^3& -{\left(A^{\ast }\right)}^D\end{array}\right).\end{array}$

定理2. 令 $H=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)$ ，其中A为方阵，如果 $BCA=0$ , $-CB{A}^{\ast }=0$ , $A{\left(BC\right)}^{\pi }=0$ , $-A^{*}{\left(CB\right)}^{\pi }=0$ ，那么

$H^D=\left(\begin{array}{cc}A{\left(BC\right)}^D-B{A}^{*}{\left({\left(CB\right)}^D\right)}^{2}C& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& -A^{*}{\left(CB\right)}^D+CAB{\left({\left(CB\right)}^D\right)}^2\end{array}\right)$ .

证明：将矩阵H分解，得

$H=\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)\text{+}\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)$ ,

令

$P=\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)$ , $Q=\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)$ ,

通过引理3，我们可以得到

$P^D=\left(\begin{array}{cc}0& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& 0\end{array}\right)$ , $P^{\pi }=\left(\begin{array}{cc}{\left(BC\right)}^{\pi }& 0\\ 0& {\left(CB\right)}^{\pi }\end{array}\right)$ .

通过条件得

$P^{2}Q=\left(\begin{array}{cc}BCA& 0\\ 0& -CB{A}^{*}\end{array}\right)=0$ ,

$Q{P}^{\pi }=\left(\begin{array}{cc}A{\left(BC\right)}^{\pi }& 0\\ 0& -A^{*}{\left(CB\right)}^{\pi }\end{array}\right)=0$ ,

因此，矩阵P和Q满足引理2，得到

$\begin{array}{c}{H}^D={\left(P+Q\right)}^D=P^D+Q{\left(P^D\right)}^2+PQ{\left(P^D\right)}^3\\ =\left(\begin{array}{cc}0& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& 0\end{array}\right)+\left(\begin{array}{cc}A{\left(BC\right)}^D& 0\\ 0& -A^{*}{\left(CB\right)}^D\end{array}\right)+\left(\begin{array}{cc}-B{A}^{*}{\left({\left(CB\right)}^D\right)}^{2}C& 0\\ 0& CAB{\left({\left(CB\right)}^D\right)}^2\end{array}\right)\\ =\left(\begin{array}{cc}A{\left(BC\right)}^D-B{A}^{*}{\left({\left(CB\right)}^D\right)}^{2}C& B{(CB)}^D\\ {\left(CB\right)}^{D}C& -A^{*}{\left(CB\right)}^D+CAB{\left({\left(CB\right)}^D\right)}^2\end{array}\right).\end{array}$

定理3. 令 $H=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)$ ，其中A为方阵，如果 $A^{2}B=0$ , , $AB=B{A}^{*}$ , $CA=A^{*}C$ ，那么

$H^D=\left(\begin{array}{cc}{A}^D+AB{\left({\left(CB\right)}^D\right)}^{2}C& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& -{\left(A^{*}\right)}^D-A^{*}{\left(CB\right)}^D\end{array}\right)$ .

证明：将矩阵H分解，得

$H=\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)\text{+}\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)$ ,

令

$P=\left(\begin{array}{cc}A& 0\\ 0& -A^{*}\end{array}\right)$ , $Q=\left(\begin{array}{cc}0& B\\ C& 0\end{array}\right)$ ,

通过条件我们得到

$P^{2}Q=\left(\begin{array}{cc}0& A^{2}B\\ {\left(A^{*}\right)}^{2}C& 0\end{array}\right)=0$ ,

$PQ+QP=\left(\begin{array}{cc}0& AB-B{A}^{*}\\ -A^{*}C+CA& 0\end{array}\right)=0$ ,

因此，矩阵P和Q满足引理1，得到

$\begin{array}{c}{H}^D={\left(P+Q\right)}^D=P^D+\left(P+Q\right){\left(Q^D\right)}^2\\ =\left(\begin{array}{cc}{A}^D& 0\\ 0& -{(A*)}^D\end{array}\right)+\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right){\left(\begin{array}{cc}0& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& 0\end{array}\right)}^2\\ =\left(\begin{array}{cc}{A}^D+AB{\left({\left(CB\right)}^D\right)}^{2}C& B{\left(CB\right)}^D\\ {\left(CB\right)}^{D}C& -{\left(A^{*}\right)}^D-A^{*}{\left(CB\right)}^D\end{array}\right).\end{array}$

下面我们给出A在矩阵H的广义Schur补 $S=-A^{*}-C{A}^{D}B=0$ 时 $H^D$ 的表达式。

定理4. 令 $H=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)$ ，其中A为方阵，如果 $S=-A^{*}-C{A}^{D}B=0$ , $A^{\pi }BC=0$ , $C{A}^{\pi }B=0$ , $AB-B{A}^{*}=0$ ，那么

$H^D=\left(\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right)E^2$ ,

其中

$E^l=F^l+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{F}^{i+l}\left(\begin{array}{cc}{A}^i{A}^{\pi }& 0\\ C{A}^{i-1}{A}^{\pi }& 0\end{array}\right),l\ge 1}$ ,

$F^l={\left(Q_2^D\right)}^l=\left(\begin{array}{c}I\\ C{A}^D\end{array}\right){\left[{\left(AW\right)}^D\right]}^{l+1}{A}^2{A}^D\left(\begin{array}{cc}I& A^{D}B\end{array}\right)$ ,

$W=A{A}^D+A^{D}BC{A}^D$ .

证明：由 $S=-A^{*}-C{A}^{D}B=0$ 可得

$H=\left(\begin{array}{cc}A& B\\ C& C{A}^{D}B\end{array}\right)=\left(\begin{array}{cc}0& A^{\pi }B\\ 0& 0\end{array}\right)+\left(\begin{array}{cc}A& A{A}^{D}B\\ C& C{A}^{D}B\end{array}\right)$ ,

令

$P=\left(\begin{array}{cc}0& A^{\pi }B\\ 0& 0\end{array}\right)$ , $Q=\left(\begin{array}{cc}A& A{A}^{D}B\\ C& C{A}^{D}B\end{array}\right)$ ,

通过条件可得 $PQ+QP=0$ , $P^2=0$ , $P^D=0$ 。由引理，我们得到

$H^D=\left(P+Q\right){\left(Q^D\right)}^2$ , (1)

接下来我们求 $Q^D$ 。

我们将Q分解为 $Q=Q_1+Q_2$ ，其中

$Q_1=\left(\begin{array}{cc}A{A}^{\pi }& 0\\ C{A}^{\pi }& 0\end{array}\right)$ , $Q_2=\left(\begin{array}{cc}{A}^2{A}^D& A{A}^{D}B\\ CA{A}^D& C{A}^{D}B\end{array}\right)$ ,

可以得到 $Q_1$ 是 $k+1$ 阶幂零的， $k=ind\left(A\right)$ ，并且 $Q_1{Q}_2=0$ ，由引理4可得

$Q^D={\displaystyle \underset{i=0}{\overset{k}{\sum }}{\left(Q_2^D\right)}^{i+1}{Q}_1^i}$ ,

其中 $Q_1^i=\left(\begin{array}{cc}{A}^i{A}^{\pi }& 0\\ C{A}^{i-1}{A}^{\pi }& 0\end{array}\right),\forall i\ge 1$ 。

下面求 $Q_2^D$ ，由引理5，

, $W=A{A}^D+A^{D}BC{A}^D$ ,

再由 $A^2{A}^D\left(\begin{array}{cc}I& A^{D}B\end{array}\right)\left(\begin{array}{c}I\\ C{A}^D\end{array}\right)=AW$ ，可以得到

${\left(Q_2^D\right)}^i=\left(\begin{array}{c}I\\ C{A}^D\end{array}\right){\left[{\left(AW\right)}^D\right]}^{i+1}{A}^2{A}^D\left(\begin{array}{cc}I& A^{D}B\end{array}\right)$ , $W=A{A}^D+A^{D}BC{A}^D$ ,

令 $E=Q^D$ , $F=Q_2^D$ ，则

$E^l=F^l+{\displaystyle \underset{i=1}{\overset{k}{\sum }}{F}^{i+l}\left(\begin{array}{cc}{A}^i{A}^{\pi }& 0\\ C{A}^{i-1}{A}^{\pi }& 0\end{array}\right),l\ge 1}$ ,

将 $E=Q^D$ 代入(1)，证毕。

基金项目

内蒙古大学校级大学生创新创业训练计划项目(项目编号：201711198)。

NOTES

^*通讯作者。