1. 引言
在本文中,我们研究如下具有衰退记忆的非经典扩散方程在强拓扑空间的适定性:
(1.1)
其中
是具有适当光滑边界的有界域。外力项
。对于非线性项,
,
且满足
(1.2)
(1.3)
其中
,l为正常数。令
对于记忆核
(参见文献 [1] [2] [3] [4] )。我们假定下列猜想:
令
,
,
,
,
,对于所有的
,
(1.4)
(1.5)
对于所有的
,
为正常数。
我们引入表示位移历史变量,定义为
(1.6)
,
(1.7)
那么方程(1.1)可转化为
(1.8)
初边值条件为
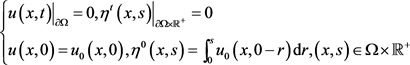 (1.9)
(1.9)
该方程作为通常的非经典扩散方程的推广情形来源并被运用于流体力学、固体力学和热传导理论领域 [5] [6] [11] 。对于某些类型的材料如聚合物和高粘度液体,其扩散过程是受u的过去历史影响,这体现在方程(1.1)中衰退记忆的卷积项对合适的存储器内核表征扩散物种 [7] 。Aifantis在文 [8] 建立了反应扩散方程的一般框架。
(1.10)
(1.11)
在反应扩散过程中如果我们考虑传播媒质的黏弹性,就需要在方程(1.11)中增加衰退记忆项,产生的模型即为我们将要研究的具有衰退记忆的非经典扩散方程。
(1.12)
据我们了解,对具有衰退记忆的非经典扩散方程解的长时间行为的研究主要集中在弱拓扑空间上。而在强拓扑空间
解的动力学行为考虑的人特别少。这里必须指出的是首先对非线性项假设仅为临界指数增长而不是任意阶指数,其次对于外力项假设具有较强的正则性,即
所以本文主要讨论在强拓扑空间下,非经典扩散方程强解的适定性。
(1.13)
为了方便,常用的一些记号和函数空间进行约定。在本文中用C记任意正常数,在不同的行中C所表示的正常数可能不同,甚至同一行中也可表示不同的正常数。记
为
的模,其内积记为
,
为
的范数,
为
的范数。令X为Hilbert空间其内积与范数分别记为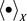 及
,记
,
,
及
,记
,
,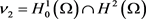 。设
是定义在
上取值于
上的一族Hilbert空间,并且赋予内积和范数:
。设
是定义在
上取值于
上的一族Hilbert空间,并且赋予内积和范数:
我们定义一族Hilbert空间:
,并且赋予范数
引理1.1:根据文献 [9] 有,令
是Hilbert空间,
,
记忆核
满足(1.4)和(1.5),则对任意的
有以下估计
(1.14)
成立。
若
,显然
,于是由 [10] 有如下引理。
引理1.2:设
,f满足(1.2)和(1.3)。初始值
,对任意
,系统(1.8)存在唯一解
,且满足以下估计:存在仅依赖于假设(1.2)~(1.5)中参数与
的正常数
和
,对任意的
及
,有
(1.15)
其中Q为严格单增的正函数。
2. 存在性
定义2.1:对任意的
,记
,设
是有界光滑区域,
满足(1.2)和(1.3),
,
是方程(1.1)的整体强解,如果z满足方程(1.1)并且
,
,
;
。
并且对于任意的
,
有
对于
几乎处处成立。
引理2.1:(强解的存在性)对于任意
,
,对任意
,
,问题(1.8)有唯一强解
满足
 ,
,
证明:设
是特征方程
,
对应于特征值
的特征函数,因此
组成
的标准正交基,即
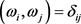 ,
,
当
时,有
,且
是
的正交基(但非标准正交基),
即为
在
中的闭线性扩张。因此
也是
的正交基。
接下来我们将构造
的一组基
。假设
是
的一组正交基,则选择
作为
的正交基
。
设
,
分别为由
和
生成的线性子空间,即
,
记
为
到
的正交投影,
为
到
的正交投影,即对任意的
有
,
,
这里
,
,
。
定义
是方程(1.1)的解,形式如下:
和
由Galerkin方法可知,它满足如下的非线性常微分方程组:
(2.1)
方程(2.1)两边用
作用,并在
上对x积分得
(2.2)
根据引理1.1有
(2.3)
利用Cauchy不等式,有
由(1.3)式,我们有
所以,我们得到
(2.4)
在
上对t积分,有
(2.5)
因此,可以得到
在
中关于
是一致有界的,
在
中关于
是一致有界的。
因此,通过Alaoglu弱紧性定理和自反性,存在
的子列
使得
在
是弱收敛,
在
是弱收敛。
为了方便起见,在不至于引起误解的情况下,在接下来的讨论中我们将
的子列仍然用
表示。
下面将证明
在
中是有界的。由
知,Sobolev嵌入
,我们有
(2.6)
其中
是嵌入常数。
因此,
由(1.2)和(2.6),使得
(2.7)
故
在
关于
是有界的,
在
是弱收敛的,这里
。
由于对任意的
,
在
,由紧性定理,
在
是强收敛的。因此
在
几乎处处收敛,利用f的连续性,有:
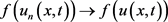 于
上几乎处处收敛,
于
上几乎处处收敛,
并有
在
上关于n一致有界,由Lebesgue逐项积分定理,对任意
有
则
在
中收敛。由弱极限的唯一性知,
。
接下来估计
。方程(2.1)两边用
作用,得
(2.8)
用Holder和Young不等式,有
和
综上
 (2.9)
(2.9)
两边在
上对t积分,得
在
中有界,在前面已经证明了
在
有界,
在
有界。因此我们有:
在
中一致有界,
在
中一致有界。
由Alaoglu弱紧性定理和自反性,知
在
是弱收敛的,
在
是弱收敛。
为了证明
是该方程的一个强解,我们还需要验证初值条件
于
成立。但基于上述估计,可由标准的方法得到(参见文献 [12] )。在此省略具体证明过程,故
为该方程满足初边值条件的整体解。
3. 强解的唯一性和稳定性
设
,
是方程(1.1)的两个解,且初值
,令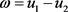 ,
,
,则
满足下面的初边值问题
,
,
,则
满足下面的初边值问题
(3.1)
方程(3.1)两边用
作用,有
(3.2)
这里
用(1.14),有:
由Holder和Young不等式和(2.7)式,得
综上,我们可以得到
其中
是与初值及常数
有关而与t无关的常数。由Gronwall引理得
当且仅当
,等号成立。所以证明解的唯一性,和对初值的连续依赖性。
致谢
本篇论文,我要感谢我的导师谢永钦教授和我的同门师姐们。从论文选题、论文的撰写、修改到最终完稿,他们都给予了我很大的帮助,再次感谢导师为我所做的一切。