基于神经网络的土壤含水量高光谱估测

Hyper Spectral Estimation of Soil Water Content Based on Neural Network

摘要: 高光谱遥感凭其极高的光谱分辨率在岩石矿物、土壤、植被等领域的应用越来越广泛。本文使用某地84个土壤样本的光谱反射数据，通过分析反射率光谱与土壤含水量之间的关系，对光谱数据进行一系列的数学变换，利用相关分析法获取的反演因子建立BP神经网络反演模型。结果表明，在土壤含水量预测研究中，利用BP神经网络建立的模型有效，且光谱变换为平方根的一阶微分时模型精度较高。

Abstract: Hyperspectral remote sensing is widely used in rock minerals, soil, vegetation and other fields due to its extremely high spectral resolution. Using the spectral reflectance data of 84 soil samples in a certain place, by analyzing the relationship between reflectance spectrum and soil water content, the BP (back propagation) neural network inversion model was established by mathematically transforming the spectral data and using the inversion factors obtained by the correlation analysis method. The results show that in the prediction of soil water content, the model established by BP neural network is effective, and the first-order differential time model with spectral transformation to square root has higher precision.

1. 引言

土壤含水量是陆地和大气能量交换过程中的重要因子，对水的运移、陆地表面蒸发、碳循环具有很强的控制作用，是生态、气候、水文、农业等领域衡量土壤干旱水平的重要指标，也是表征土壤肥力的重要指标。传统的土壤水分测定方法，如取土烘干法、张力计法、中子水分仪法等均是以点测量为基础，虽然精度高，但工作量大，范围有限，已经难以满足区域性土壤含水量监测的实际需要；土壤水分模型方法通过建立水分平衡方程求解土壤水分，可提供适时的土壤水分信息，但实验需要大量相关参数，估测误差较大。用遥感反演手段获取土壤含水量，具有范围大、时间短、分辨率高的特点，弥补了传统方法上的不足。其中高光谱遥感是利用多波段的电磁波从物体中获取有关数据，波段划分更窄，能获取更多的窄波段的光谱信息，产生一条完整而连续的地物光谱曲线 [1] [2] [3] [4] [5] 。本文采用了BP神经网络模型对土壤水含量进行了反演，利用多层神经网络可以寻找最优因子，建立的土壤水分含量的预测模型精度高，且为快速准确预测土壤含水量提供理论依据。

2. 土壤含水量BP神经网络估测模型

人工神经网络是基于生物神经网络原理由大量简单处理单元相互连接而形成的复杂网络系统，它具有较强的学习能力、抗干扰能力、容错能力 [6] 。人工神经元相当于一个多输入多输出的非线性阑值器件。其神经元的输出可以描述为：

(1)

式中： $x_1,x_2,\cdots x_n$ 为输入信号， ${\omega }_{k1},{\omega }_{k2},\cdots {\omega }_{kj}$ 为神经元k的权值， ${\theta }_k$ 为阈值，f为激活函数， $y_k$ 为神经元k的输出。

人工神经网络中较为典型的神经网络模型有BP神经网路、Hopfield网络、CPN网络等，应用较多的是具有非线性传递函数神经元构成的前馈网络中采用误差反向传播算法作为其学习算法的前馈网络(Back Error Propagation，BP) [7] 。BP网络包含了神经网络理论中最精华的部分，由于其结构简单、可塑性强，得到了广泛的应用。特别是它的数学意义明确、步骤分明的学习算法更使其具有广泛的应用背景。BP网络由输入层、输出层和若干隐含层组成，并且一般认为网络是严格分层的，即当且仅当两相邻层的节点才有可能互联。简单的三层BP网络的结构如图1所示。

BP神经网络计算模型如下

Figure 1. BP network structure diagram

图1. BP网络结构图

$y=f^2\left({\theta }^2{f}^1\left({\theta }^{1}x+b^1\right)+b^2\right)$ (2)

其中，y为输出层，x为输入层， $f^1$ 为隐藏层传递函数， $f^2$ 为输出层传递函数， $b^1$ 为隐藏层偏差， $b^2$ 为输出层偏差， ${\theta }^1$ 为输入层权重， ${\theta }^2$ 为隐藏层权重 [8] 。

3. 算例

以某地的土壤区作为研究对象，其主要土地利用类型为耕地、林地、牧草地、未利用地(沙地、废弃地)、建设用地等，选择地势较平坦、土壤裸露区作为样区，并考虑各种土地利用类型和土壤类型，每个样区内选择4~5个具有代表性的测点，每个测点采集一个表层土(约20 cm)土样，共采集84个土样。

3.1. 光谱数据的平滑处理

光谱曲线的平滑处理是为了去除包含在信号内的少量噪声，得到平稳的光谱波形。采用9点加权移动平均方法对光谱数据进行平滑处理。若给出了光谱曲线的n个测点的序列 $\left(R_i,i=1,2,\cdots ,n\right)$ ，则第 的值取包含前后各9个点的加权平均值 [9] ，即

$\begin{array}{l}{R}_i=0.04{R^{\prime }}_{i-4}+0.08{R^{\prime }}_{i-3}+0.12{R^{\prime }}_{i-2}+0.16{R^{\prime }}_{i-1}+0.20{R^{\prime }}_i+0.16{R^{\prime }}_{i+1}\\ +0.12{R^{\prime }}_{i+2}+0.08{R^{\prime }}_{i+3}+0.04{R^{\prime }}_{i+4}\end{array}$ (4)

式中， $R_i$ 表示9点平滑处理后的值。经平滑处理后形成新的光谱曲线的n个测点的序列 $\left(R_i,i=1,2,\cdots ,n\right)$ 。

3.2. 光谱数据变换方法

为了寻找对有含水量敏感的光谱指标，主要采用的变换方法如表1所示。

利用变换方法对光谱数据进行变换，并与含水量进行相关分析，得到反射率及其各种变换形式与含水量相关系数和包络线去除得到的各种参量与含水量的相关系数。如图2所示。由图可看出，反射率R倒数的对数、对数的一阶微分、平方根的一阶微分与含水量的相关系数较大，数据在峰值处大于0.6，表明其相关性较大，适宜线性模型的建立，而倒数、对数的倒数相关系数达到0.6的波段较多，但是峰值较少，不适合模型的建立。

光谱反演因子选取是挖掘光谱中蕴含的有效信息，通过对各种变换方法认真比较，最终选择在通过一阶微分变换、对数的一阶微分变换和平方根的一阶微分变换中选取反演因子。

采用单相关分析方法提取光谱反演因子，顾及相邻波段间的光谱数据相关性较高，在选择波段时尽量使其离散化。利用一阶微分变换、对数的一阶微分变换和平方根的一阶微分变换各选取了5个波段数据作为反演因子。

Table 1. Transformation method table

表1. 本文使用的变换方法表

Figure 2. Transformation comprehensive map

图2. 变换综合图

3.3. 数据处理过程

异常样本(落在总体之外的数据点)的产生是人为测量过程中带来的误差，包括土壤属性的化学测定和土壤光谱数据的测量产生的异常数据，异常值的存在可能会影响模型的准确性建模之前要先对异常样本进行删除。李希灿等提出剔除异常样本的方法是，首先对土壤含水量从小到大进行排序，对应的反演指标也进行排序，分别绘制排序后的土壤含水量和反演指标的分布曲线，然后，在分布曲线的两端寻找异常样本 [10] [11] 。

一共剔除了3个异常样本，在剔除异常样本之后R2明显增大。把剔除异常样本后剩余的81个样本分成两组，一组66个样本为建模样本，另一组15个样本为检验样本。

利用变换后的光谱数据与土壤含水量相关关系曲线选取的反演因子，光谱数据与土壤含水量建立BP神经网络模型。将BP神经网络的隐含层数设为1~3层，隐节点数设在4~5个之间，隐含层传递函数采用logsig函数或者tansig函数，输出层传递函数采用purelin函数，网络训练函数采用traincgh函数或者trainlm函数。基于特征吸收波段的分析建模时，将66个将反射率变换之后的数据按照BP神经网络输入向量，水含量实测值作为输出向量，通过网络中隐含层节点数、隐含层数这2个参数的不同组合，得到一系列的模型，然后分析误差从而得出最佳模型。

4. 结果分析

将81个样本数据分为两组，66个用于网络训练、15个用于模型检验。基于BP神经网络法建立了多个土壤水含量的高光谱反演模型，如表2~4所示，结果表明，用真实含水量与预测值做差，在剔除差

Table 2. Accuracy comparison between first-order differential models of square roots

表2. 平方根的一阶微分模型之间的精度对比

Table 3. Accuracy comparison between first-order differential models

表3. 一阶微分模型之间的精度对比

Table 4. Accuracy comparison between first-order differential models of logarithms

表4. 对数的一阶微分模型之间的精度对比

距较大的样本后，取含水量与预测值差值平方和，平方根的一阶微分神经网络模型，平均相对误差值最小，为11.949，决定系数最大，为0.922。

对前述的反演因子分别建立土壤含水量的多元线性回归估测模型、BP神经网络估测模型，精度分析如图3，图4所示，详细数据如表5和表6所示。BP神经网络的决定系数为0.922，多元线性回归模型的决定系数为0.869，通过比较可以得出BP神经网络模型预测值与实测值较为接近。

5. 结束语

研究采集了某地0~20 cm表层土84个土壤样品，用标准化学方法测得土壤样品的水含量，并在实验室内测定了土壤样品的反射率光谱。运用BP神经网络法建立了含水量的多个反演模型，并对模型进行

Figure 3. BP neural network test sample accuracy analysis chart

图3. BP神经网络检验样本精度分析图

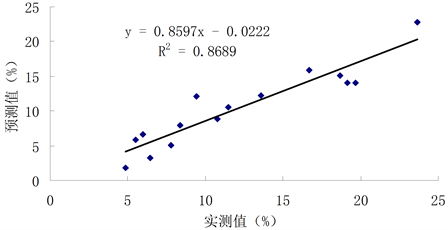
Figure 4. Multiple linear regression test samples accuracy analysis chart

图4. 多元线性回归检验样本精度分析

Table 5. BP neural network test sample accuracy analysis table

表5. BP神经网络检验样本精度分析表

Table 6. Linear regression test sample accuracy analysis table

表6. 线性回归检验样本精度分析表

了验证。土壤水含量与土壤光谱之间的关系比较复杂，具有一定的不确定性。对样本的光谱反射率数据与土壤含水量进行分析，利用平方根的一阶微分得到的模型精度最高，其中平均相对误差值为11.949%，决定系数为0.922。由于土壤含水量与高光谱反射率之间并不存在严格意义上的线性关系，采用神经网络的方法进行反演建模，虽然是非线性分析方法，但是要更准确地揭示土壤含水量与高光谱反射率之间的内在联系，有待进一步实验与研究。