一种多分辨率体绘制中张量分解最佳秩选取算法

An Algorithm for Choosing Optimal Rank in Tensor Approximation of Multi-Resolution Volume Rendering

摘要: 采用多分辨率体绘制是解决海量数据体绘制的一种有效方法，但是基于信息熵的多分辨率体绘制在解决信噪比低、细微结构复杂的物探领域内体数据时存在较大的缺陷。而数据的张量近似是通过高阶奇异值分解提取数据的特征基，并通过特征基的线性组合来近似包含细微结构的低信噪比体数据。因此可以在保证数据压缩率的情况下，保留数据的细微构造信息。本文针对基于张量近似的多分辨率体绘制中秩的选取问题开展研究，低秩实现了高的数据压缩，但峰值信噪比低；高秩实现了较好的绘制效果，但数据压缩率低。本文提出了一种张量近似中最佳秩的选取算法。其基本思想是在高秩分解的基础上，通过二分搜索选取满足误差门限的最佳秩。并且，数据分块处理，不同分块采用不同秩，实现了在满足数据压缩率的情况下，保证有较好的绘制效果。通过仿真结果表明，相比于统一秩的高秩分解而言，提升了数据压缩率，而整体绘制效果基本与高秩分解相当；相比于统一秩的中低秩分解而言，在增加少量的压缩率的情况下，提升了绘制效果。

Abstract: Multi-resolution volume rendering is an effective method to solve the problem of massive data volume rendering. The comentropy based multi-resolution volume rendering has an obvious limitation when handling data of geophysical field which have a low SNR and complex microstructure characteristics. Tensor approximation can extract the characteristic bases of the data, and gain the data approximation with microstructure characteristics by means of the linear combination of the characteristic bases. We made a research about how to choose the rank in tensor approximation multi-resolution volume rendering. Low rank gained a high compression ratio, but low PSNR. High rank gained an ideal rendering effect, but low compression ratio. In this paper, we presented a method that could find the best rank adaptively for every block. Based on high rank decomposition, we did binary search to find the optimal rank which will exactly meet the error threshold. Mean-while, data were separated into blocks, different blocks have different ranks. Experimental results show that our method has a higher compression ratio and similar render result in comparison with high rank decomposition and our method has a significant better rendering result and a slightly lower compression ratio.

1. 引言

当前，基于GPU加速的直接体绘制技术 [1] 已经成为交互处理体数据的标准方法。相比于传统表面绘制，体绘制技术可以反映物体的内部结构。因此能够被广泛应用于许多领域中，例如：医学领域、流体物理领域、气象领域、地质勘探领域等等。

尽管近几年图形硬件设备发展迅速，但是GPU存储空间的限制，依然是制约体绘制技术发展的主要瓶颈 [1] 。在这种情况下，产生了多分辨率体绘制技术。多分辨率体绘制技术是通过将数据体划分为不同的分块，每一个分块赋予不同的分辨率来实现压缩数据量和减少绘制点数。每个分块的分辨率又被称为分块的LOD (level of detail, 细节水平)。因此，多分辨率技术的关键即为如何确定每一个分块的细节水平。

近年来常用的多分辨率的数据组织形式有两种：基于统一划分的形式和基于层次划分的形式。

Ljung P等 [2] 提出了基于统一划分的多分辨率体绘制技术。在统一划分中，每个分块各自独立地确定自己的分辨率，分块与分块之间互不影响。Ljung等 [3] 提出了基于CIELUV (CIE 1976 (L*, u*, v*) color space)空间的误差准则。并且在分块细节水平选择时，引入了传递函数的信息，以此来优化绘制效果。梁荣华等 [4] 提出了基于信息熵的分块细节水平选择方法，并能够自适应的优化用户设定的阈值，以提高绘制效果。

Boada I [5] 等首先提出了基于八叉树的多分辨率数据表示。用一颗八叉树来表示整个三维数据体。每一个节点代表一个分块。将空间中8个相邻的分块重采样成一个相同大小的分块，即构成了这8个分块的父分块。父分块对应八叉树中，这个8个分块所对应节点的父节点。因此，每个分块的点数相同，但其所代表的空间中的实际大小不同。通过对八叉树的遍历，能够很容易地实现对每个分块的随机访问。八叉树多分辨率的很多研究集中在，如何在硬件的限制下确定每一个节点的误差。砖块与视点的距离，感兴趣的区域和块内部数据的同质性以及近似后的误差 [6] [7] [8] 通常被用来确定一个分块的细节水平。Guthe和Straber [9] 提出了一种对失真误差的保守估计方法。他们将误差定义为最大的RGB误差和最大的不透明度误差的和。Ljung [10] 用简化的1维直方图去近似每个分块和它原始分块的均方误差。

张量近似 [11] [12] [13] 是用高阶奇异值分解等工具来实现对体数据的近似，其可以被看做是主成成分分析在高维数据中的推广。目前主流的张量近似技术是将一个体数据表示成一系列秩1张量的和或者是一个核心张量和三个因子矩阵的乘积。前者被称为CP (canonical decomposition)分解，后者被称为Tucker分解。被常用于体绘制中的是Tucker分解，因为其每一个因子矩阵就代表了原始数据的每一个方向上的结构特征，因而Tucker分解能够产生具有三维数据特征的基，对于特征提取有十分重要的作用。大量实验验证了Tucker模型比CP模型在大多数三维可视化中有更好地性能和效果，更具有实用性。Tucker分解的数据压缩通过秩截断来实现。Susanne K. Suter [12] 等证明了秩截断张量近似与离散小波变换相比，在相同数量的系数下，更能够捕获到数据体任意方向上的三维特征。因此，张量近似能够很好应用于体数据的压缩和特征提取当中。

但是，秩截断技术中，一个关键的问题是如何选取张量分解的秩。如果选取的秩太大，会直接影响数据的压缩率和噪声的过滤；如果选取的秩太小，又可能会导致表征数据的基向量的个数不足，信息量不够，近似误差太大。同时，对于一个三维数据体来说，其微结构特征可能呈区域状分布。这就意味着，对于不同的分块来说，其蕴含的结构特征的多少可能差别很大。如果对所有分块用相同的基向量个数，即统一大小的秩，则对有些分块来说，可能会导致误差过大；对另外一些分块来说，可能会造成不必要的压缩率损失。因此，我们需要对每一个分块赋予其最合适的秩。因此，本文提出一种能够自适应地为每一个分块寻找最佳秩的方法。

2. 高阶张量近似原理

张量近似是一种基于高阶奇异值分解(HOSVD) [11] [12] [13] 的一种数据近似算法。目前常用的三阶张量近似主要有两种方式：Tucker模型和CP模型。由于Tucker模型产生的三个因子矩阵恰好和三维体数据的三个维度有关，再加上大量文献 [13] [14] [15] 已经证明了Tucker模型比CP模型在体绘制中具有更好的表现。因此，本文所选用的张量近似模型为Tucker模型。

张量分解其实可以看作是矩阵奇异值分解在更高维度上的推广。如图1所示，基于Tucker模型的3阶张量分解能够将一个3阶张量分解为一个核心张量和3个因子矩阵。

对于一个n阶的张量A，其维度为 $I_1\times I_2\times \cdots \times I_n$ ，我们可以将其用一个核心张量B和n个因子矩阵 $U^{\left(1\right)},U^{\left(2\right)},\cdots ,U^{\left(n\right)}$ 的TTM [10] 乘积来表示，其中核心张量B的维度为 $R_1\times R_2\times \cdots \times R_n$ ，因子矩阵 $U^{\left(i\right)}\left(1\le i\le n\right)$ 的大小为 $I_i\times R_i$ ：

$A\approx B{\times }_1{U}^{\left(1\right)}{\times }_2{U}^{\left(2\right)}{\times }_3\cdots {\times }_n{U}^{\left(n\right)}$ (1)

其中， $\left(R_1,R_2,\cdots ,R_n\right)$ 称为Tucker分解的秩，上述的过程我们称为对张量A的秩 $\left(R_1,R_2,\cdots ,R_n\right)$ 分解。因子矩阵U⁽ⁿ⁾ 的大小为 $I_n\times R_n$ ，其行数I_n代表原始数据体I_n方向上点的个数，即数据体在方向n上的基的维数，其列数R_n代表该方向上的基的个数。其每一列r，则表示数据体在方向n上的一个基。因此，

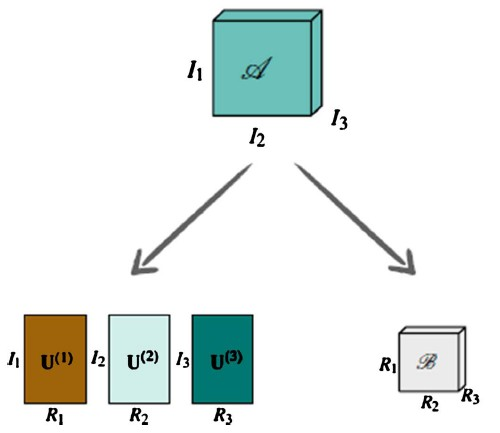
Figure 1. Tucker model tensor decomposition

图1. 基于Tucker模型的张量分解

整个因子矩阵U⁽ⁿ⁾ 组成了数据在方向n上的一组基。

3. 秩截断技术分析

从前面可知，因子矩阵的列数代表了基的个数，即该方向信息量的大小，基的个数越多，信息量越大，重构越精确。并且越前面的列，所包含的信息越重要，越能反应出数据体的结构特征；对应的，越后面的列，越能反应数据体的细节 [16] 。因此，为了凸显数据体的结构特征，同时增加压缩率，我们可以进行秩截断，即选取因子矩阵的前r列构成的子矩阵作为新的因子矩阵，同时，选取核心张量中对应的子块作为新的核心张量。由这样的子因子矩阵和子核心张量重构出的数据体，能够忽略掉部分无关紧要的细节特征，同时最大程度的凸显结构特征，如图2所示：秩由(R₁, R₂, R₃) 截断为(K₁, K₂, K₃) 。

Figure 2. Rank truncation

图2. 张量近似秩截断

张量重构的过程相比于张量分解就简单得多，只需要根据式(1)将核心张量B和因子矩阵 $U^{\left(1\right)},U^{\left(2\right)},\cdots ,U^{\left(n\right)}$ 依次作TTM乘积，就能够重构出原始张量的近似值。

目前，秩截断技术的主要限制是，统一秩分解会导致某些分块误差过大，而另一些分块压缩率不足 [17] [18] 。我们用峰值信噪比(PSNR)来表示处理后的数据和原始数据的差异大小，PSNR的定义如式(2)，(3)所示：

$\text{MSE}=\frac{{{\displaystyle \sum }}_{n=0}^N{\left(a_n-b_n\right)}^2}{N}$ (2)

$\text{PSNR}=10\times {\log }_{10}\frac{K^2}{\text{MSE}}$ (3)

其中，N为数据的总点数，a_n，b_n 分别表示某一数据点经过处理前后的值，K表示数据体的变化范围。据此，可以得到对某一地震数据进行秩截断后，峰值信噪比大小如表1所示。

Table 1. PSNR and compression ratio

表1. PSNR与压缩率

可见，高秩分解具有高峰值信噪比，但压缩率不足，低秩分解具有理想的压缩率，但峰值信噪比低。所以，如果对所有分块用统一大小的秩，则对有些分块来说，可能会导致误差过大；对另外一些分块来说，可能会造成不必要的压缩率损失。因此，我们需要对每一个分块赋予其最合适的秩。

4. 最佳秩选取算法

为了为每个分块寻找其最佳大小的秩，在保证其最终的绘制效果的基础之上尽可能多的压缩数据，我们从一个初始大小的秩开始，进行二分搜索，直到找到一个最佳的秩，即恰好满足误差门限的秩。

我们首先对分块数据进行初始的高秩分解。在初始的高秩分解的基础上，我们从设定好的初始秩开始，对张量分解的秩进行二分查找，从中找到该分块数据的最佳秩大小。

寻找分块的最佳秩的过程，是一个试探的过程。当然，我们可以通过从低到高遍历来找到最佳的秩。但是，当秩的个数很大时，这种搜索方式的效率太低。对于一个分块数据来说，最佳的秩大小即为刚好满足误差门限的秩。这就意味着，大小比最佳秩大的秩，其重构误差必然小于误差门限；大小比最佳秩小的秩，其重构误差必然大于误差门限。利用这一特性，我们可以采用二分搜索的思想来提高寻找最佳秩过程的效率。

图3展示了二分搜索最佳秩的流程。假设我们要从r₁ 到r_n 中，寻找最佳大小的秩。我们首先判断r₁ 的重构误差是否小于误差门限。如果小于，则二分搜索结束，最佳秩为r₁；否则，取r₁和r_n 的中点(r₁ + r_n)/2作为下一个要判断的秩。若(r₁ + r_n)/2的重构误差小于门限值，则说明最佳秩在r₁到(r₁ + r_n)/2之间，则取r₁ 到(r₁ + r_n)/2的中点为下一个要判断的秩，继续上述过程；若(r₁ + r_n)/2的重构误差大于门限值，则说明最佳秩在(r₁ + r_n)/2到r_n之间，则取(r₁ + r_n)/2到r_n 的中点为下一个要判断的秩，继续上述过程。搜索的结束条件为不能继续对两个端点进行二分取值。当结束条件满足时：如果当前秩的误差小于门限值，则当前秩为最佳秩；如果当前秩的误差大于门限值，则最佳秩为当前秩加1。

因此，我们将从r₁到r_n中搜索最佳秩的算法步骤归纳如下：

第一步：当前秩R = r₁ ，起点R_s = r₁，终点R_e = r_n；

第二步：对分块做秩R截断，计算重构误差；

第三步：若误差小于门限值，跳到步骤4；若误差大于门限值，跳到步骤5；

第四步：若R − R_s < 2，输出R，算法结束；否则，R_e = R，R = (R_s + R_e )/2，跳到步骤2；

第五步：若R_e − R < 2，输出R +1，算法结束；否则，R_s = R，R = (R_s + R_e)/2；跳到第二步；

如果在二分查找的每一次比较中都进行完整的张量分解和重构的话，对每一个块的秩选取会耗费大量不必要的时间。张量重构的过程很快，因此不需要做额外处理。对于张量分解，我们采用因子矩阵和

Figure 3. Binary search for optimal rank

图3. 二分搜索最佳秩流程

核心张量秩截断的方式来替代对每一次秩试探所做的张量分解。如图3所示，根据因子矩阵的特性，越前面的列代表了该方向越重要的基，越后面的列对数据的贡献越小。因此，我们可以对因子矩阵的列和其对应的核心张量作截断，来达到减小秩的目的。根据上一节介绍的秩截断原理，对U⁽¹⁾，U⁽²⁾和U⁽³⁾秩

截断后，得到新的低秩因子矩阵 $U_{k1}^{\left(1\right)}$ ， $U_{k2}^{\left(2\right)}$ 和 $U_{k3}^{\left(3\right)}$ ，以及对应的核心张量 B_k1k2k3。于是我们将高秩分解(R₁, R₂, R₃) 截断成了低秩分解(K₁, K₂, K₃) 。

因此，我们的自适应秩选择过程从一个初始的高秩分解开始。从实践中，我们得到R = I/2无论从近似效果和压缩率来说，都是比较好的张量分解的秩的选择，因此我们也将它作为自适应秩选择的初始的高秩分解的秩。由于我们的分块大小一般设置为32，因此，我们初始时对块做秩16分解。另外，我们还需要设定秩截断的初始秩大小。在对地震数据的张量近似实验中，我们发现当R = 4时，因此，我们设定秩截断的初始秩大小为R = 4。

误差的计算可以根据实际的需要选择合适的标准。本文采用的是矩阵的Frobenius范数作为重构误差的标准：

$e=\frac{{\Vert A-\tilde{A}\Vert }_F}{{\Vert A\Vert }_F}$ (4)

其中，e代表重构后的归一化误差，A代表原始张量， $\tilde{A}$ 代表重构后的近似张量，对大小为M×N的矩阵B做 ${\Vert \Vert }_F$ 运算定义为：

${\Vert B\Vert }_F=\sqrt{{\displaystyle {\sum }_{i=1}^M{\displaystyle {\sum }_{j=1}^N{b}_{ij}^2}}}$ (5)

5. 仿真分析

在最佳秩选取的仿真中，在各个方向上我们采用相同的秩。搜索的初始秩为4，最高秩为16。为了验证本文的方法确实能够实现自适应地分块秩截断，在仿真过程中，我们记录了不同误差门限下每个秩大小下包含的分块数目。为了方便，我们只设置了4个不同的分块秩等级，分别为4，8，12和16。如表2所示，本文的方法确实能够实现分块最佳秩选取，并且误差门限越高，整体的分块秩大小越低，压缩效果也就越高。图5展示了不同误差门限值下的分块最佳秩选取效果图。从图4中可以看出，随着误差门限的增大，最佳秩选取后的整体绘制效果开始逐渐变差。

Table 2. Blocks distribution under different threshold by rank

表2. 不同误差门限下的秩对应分块个数分布

(a) T_e = T_p = 0.1; (b) T_e = T_p = 0.2; (c) T_e = T_p = 0.3; (d) T_e = T_p = 0.4

Figure 4. Optimal rank rendering result under different threshold

图4. 不同门限值的最佳秩选取效果图

为了对比本文的最佳秩选取算法与统一秩张量分解的性能差异，我们记录了它们各自的压缩率和预处理时间，为了使不同大小的秩的分块数近似满足正态分布的特点，我们选取T_e = T_p = 0.25作为秩截断的误差门限，如表3所示。在压缩率方面，误差门限为T_e = T_p = 0.25的最佳秩选取的压缩率远远优于统一的秩(16, 16, 16)分解，而比统一的秩(8, 8, 8)和秩(4, 4, 4)分解稍差。在预处理时间方面，误差门限为T_e = T_p = 0.25的最佳秩选取比统一秩(16, 16, 16)分解多不到20%，比统一秩(8, 8, 8)和秩(4, 4, 4)分解多60%左右。

同时，本文还对比了最佳秩选取和统一秩分解的效果差异，如图5所示。可以看出，误差门限为T_e = T_p = 0.25的最佳秩选取张量分解的整体绘制效果不逊于统一秩(16, 16, 16)分解，甚至在某些微结构特征的表现上还要优于统一秩(16, 16, 16)分解。而统一秩(8, 8, 8)分解和统一秩(4, 4, 4)分解的绘制效果则明显不如最佳秩选取。

Table 3. Comparison between optimal rank and unified rank

表3. 最佳秩选取和统一秩分解性能对比

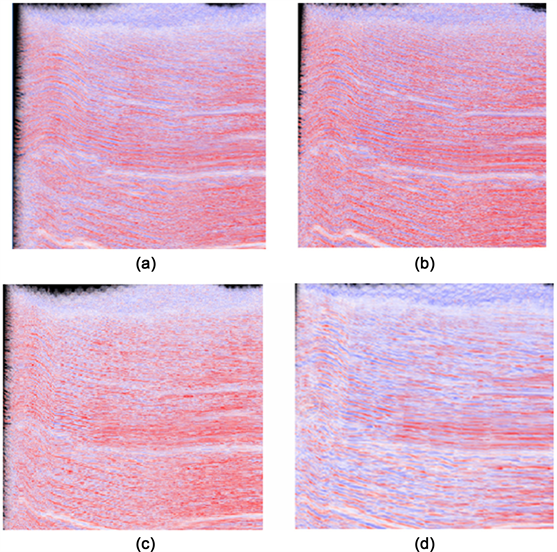(a)T_e = T_p = 0.25，最佳秩；(b)统一秩(16, 16, 16)分解；(c)统一秩(8, 8, 8)分解；(d)统一秩(4, 4, 4)分解

Figure 5. Comparison between optimal rank and unified rank

图5. 最佳秩选取和统一秩张量分解效果对比

由此，我们可以得出结论：最佳秩选取相比与统一秩的高秩分解来说，牺牲了少量的预处理效率，换来了出色的压缩率提升，而且其整体绘制效果丝毫不逊于高秩分解，而且在某些微结构特征的表现方面还要优于高秩分解。而相比于统一秩的中低秩分解来说，最佳秩选取以少量的压缩率和不多的预处理效率为代价，获得了出色的绘制效果提升。

6. 结束语

针对基于张量近似的多分辨率体绘制方法中，张量分解时秩选取的问题，本文提出了一种能够自适应地为每一个分块寻找最佳秩的方法。该方法可以在牺牲了少量的预处理效率的情况下，得以大幅提升压缩率，并且能够得到不逊于高秩分解的整体绘制效果，而且在某些微结构特征的表现方面还要优于高秩分解。对于本文方法所带来的预处理时间上的牺牲，可以采用并行计算、多线程计算、GPU加速等方法来提高本文方法的预处理时间。

基金项目

四川省教育厅自然科学科研项目(16ZB0444)。

NOTES

^*通讯作者。