保费依赖余额模型的最优分红问题

Optimal Dividend Problem for the Risk Model with Surplus-Dependent Premiums

摘要: 本文研究了保费依赖余额模型的最优分红问题。目标是最大化破产前的累积期望折现分红，首先，我们给出值函数的基本性质，然后运用测度值生成元的理论得到测度值动态规划方程(测度值DPE)。

Abstract: In this paper, we consider the optimal dividend problem for the risk model with surplus-dependent premiums. The objective is to maximize the expected cumulative discounted dividends payment up to the time of ruin. Firstly, we show the basic properties of the value function. Using the theory of measure-valued generators, we derive the associated measure-valued dynamic programming equation (measure-valued DPE).

1. 引言

1930年，Lundberg-Gramer提出了经典的累积风险模型，该模型常用来研究保险公司的分红及破产概率。而为了使得描述的风险模型更加地贴近实际，1984年，Davis提出了更加一般的保险风险模型，他们称为逐段决定复合泊松风险模型。该模型是一般的模型，囊括了多种目前常见的风险模型。在本文中，我们假设保险公司的风险模型是保费依赖余额(逐段决定复合泊松风险)模型，即余额过程为逐段决定马氏过程(PDMP)。PDMP自提出以来就受到金融，保险，随机控制等多个领域的广泛关注，也涌现出了大量关于PDMP的文章。如 [1] - [6] 研究了PDMP的连续和脉冲控制，最优停时，在风险中的应用等。关于保险中PDMP的相关内容可以参考Schimidlli [7] 。随后，PDMP也被应用到最优分红问题的研究中。

最优分红问题最早可追溯到 [8] ，De Finetti在第15届国际精算学大会(纽约)上首次提出了破产前累积期望折现分红的概念，并对离散时间风险模型的最优分红问题进行了研究，并得到最优分红是barrier策略。通常，研究最优分红问题的方法为Schimidlli的经典方法和Muller [9] 的粘性解的方法(关于最优分红的问题可参考Muller [9] )。在2017年，Liu在 [10] 中提出了一种新的理论：测度值生成元理论。本文即运用该理论得出测度值动态规划方程，该方法不要求值函数是光滑的，则我们不需要讨论方程的粘性解。

本文结构如下：第1节建立保费依赖余额的保险风险模型，并给出相应的最优分红问题。第2节给出了值函数的基本性质。第3节通过测度值生成元理论给出了测度值动态规划方程(测度值DPE)。

2. 模型描述

首先给出完备的概率空间( $\Omega$ , F, P)， $\Omega$ 是所有右连续且有左极限的函数集合。在此空间内，将保险公司的余额X表示为

$X_t=x+{\displaystyle {\int }_0^{t}g\left(X_s\right)\text{d}s}-{\displaystyle \underset{i=1}{\overset{N_t}{\sum }}{Y}_i},t\ge 0$ (1.1)

其中， $x\ge 0$ 为初始余额， $N_t$ 表示到t时刻的索赔个数。索赔额序列 $\left\{Y_i\right\}$ 为一独立同分布的随机变量序列，其分布函数为 $Q\left(x\right)$ ，并且 $\left\{Y_i\right\}$ 和 $N_t$ 是相互独立的。索赔到达率 $\lambda >0$ 为常数，则下次索赔达到时刻的条件概率分布为 $F\left(x,t\right)=e^{-\lambda t}$ 。 ${\tau }_n$ 表示第n次索赔时刻，在两个连续的索赔时刻间的余额过程可表示为

$X_t={\phi }_{X_{{\tau }_n}}\left(t-{\tau }_n\right),t\in \left[{\tau }_n,{\tau }_{n+1}\right],n\in N,$

定义推移算子 $$ ，满足 $X_{s+t}=X_t\cdot {\theta }_s$ 。

$L=L_t,t\ge 0$ 为从0时刻到t时刻的累计分红。给定分红策略L，受控的余额过程 $X_t$ 可表示为

$X^{L_t}=x+{\displaystyle {\int }_0^{t}g\left(X_s^L\right)\text{d}s-{\displaystyle \underset{i=1}{\overset{N_t}{\sum }}{Y}_i}-L_t},$ (1.2)

相应的破产时刻定义为

${\tau }^L=\inf \left\{t\ge 0:X_T^L<0\right\}.$

在任意时刻t，索赔到达率都为 $\lambda$ ，受控后的条件概率分布不变。

如果L满足下列条件，则称L为可行策略。

1) $L_t$ 是非降且关于自然流 ${\left\{F_t\right\}}_{t>0}$ 是适应的；

2) 过程 $L_t$ 满足

$L_t\le x+{\displaystyle {\int }_0^{t}g\left(X_s^L\right)}\text{d}s-{\displaystyle \underset{i=1}{\overset{N_t}{\sum }}{Y}_i},$

3) 方程(1.2)有唯一强解 $X^L$ 。

定义 ${\Pi }_x$ 是所有以 $x\ge 0$ 为初始余额的可行策略集。

对每个分红策略 $L\in {\Pi }_x$ ，累积期望折现分红 $V^L\left(x\right)$ 可表示为

$V^L\left(x\right)=E\left[{\displaystyle {\int }_0^{{\tau }^L}{e}^{-\delta s}\text{d}{L}_s|X_0=x}\right]=E_x\left[{\displaystyle {\int }_0^{{\tau }^L}{e}^{-\delta s}\text{d}{L}_s}\right],$

其中 $\delta >0$ 是折现因子。定义值函数

$V\left(x\right)=\sup \left\{V^L\left(x\right),\backslash ;L\in {\Pi }_x\right\},x\ge 0$ 。

通常，当 $x<0$ 时， $V\left(x\right)=0$ 。

3. 值函数性质

引理2.1：值函数 $V\left(x\right)$ 是非降的，局部Lipschitz连续且满足

$y-x\le V\left(y\right)-V\left(x\right)\le \frac{\delta +\lambda }{g\left(0\right)}V\left(y\right)\left(y-x\right)$

$y>x\ge 0$ 。

证明：取分红策略 $L\in {\Pi }_x$ 使 $V^L\left(x\right)\ge V\left(x\right)-\epsilon \left(\epsilon >0\right)$ 。对任意的 $y>x\ge 0$ ，重新定义一个新策略 $\bar{L}\in {\Pi }_x$ ，该策略先将 $y-x$ 作为分红一次性分给股东，之后有 $\bar{L}=L$ ，则有下列不等式成立

$V\left(x\right)\ge V\overline{{}^L}\left(x\right)+y-x\ge V\left(x\right)+y-x-\epsilon$

则 $y-x\le V\left(y\right)-V\left(x\right)$ ，同时可得V是非降的。

下证 $V\left(y\right)-V\left(x\right)\le \frac{\delta +\lambda }{g\left(0\right)}V\left(y\right)\left(y-x\right)$ 。

令 $y={\phi }_{x\left(t\right)}$ ，则有

$\begin{array}{c}V\left(y\right)-V\left(x\right)\le [1-{\text{e}}^{-\left(\delta t+\lambda t\right)}]V\left({\phi }_x\left(t\right)\right)\\ \le \left[1-{\text{e}}^{-\left(\delta t+\lambda t\right)}\right]V\left(y\right)\\ \le \left[\delta +\lambda \right]tV(y)\end{array}$

由于g是单调递增的，有 $t\le \frac{y-x}{g\left(0\right)}$ ，则不等式成立且V是局部Lipschitz连续的。

4. 动态规划原理(DPP)及动态规划方程(DPE)

定义 $U_x$ 是可测函数 $\alpha (\cdot ):R_{+}\mapsto \left[0,l_0\right]$ 的集合， $\alpha (\cdot )$ 满足下列条件：

$x\ge 0$ ，方程 ${\phi }_x^{\alpha }\left(t\right)=x+{\displaystyle {\int }_0^{t}g\left({\phi }_x^{\alpha }\left(s\right)\right)\text{d}s-\alpha \left(t\right)}$ 有唯一解 ${\phi }_x^{\alpha }$ ；

$t\ge 0$ ， $\alpha \left(t\right)\le x+{\displaystyle {\int }_0^{t}g\left({\phi }_x^{\alpha }\left(x\right)\right)\text{d}s}$ 。

下面我们给出马氏策略及马氏策略集合的定义。

定义4.1：如果受控后的余额过程 $X^L$ 是强马氏过程，称 $L\in {\Pi }_x$ 是马氏控制；如果 $X^L$ 是时齐的强马氏过程，则称L为平稳的马氏控制。

定义 $M$ 为可测函数 $L(\cdot ):R_{+}\mapsto \left[0,l_0\right]$ 的集合，且 $l(\cdot )$ 满足

1) $x\ge 0$ ， $l\left(x,\cdot \right)\in U_x$ 。

2) 对任意 $x\ge 0$ ， $s,t\ge 0$ ，有

$l\left(x,s\right)+l\left({\phi }_x^l\left(s\right),t\right)=l\left(x,s+t\right)$

3) 当 $t\in \left[{\tau }_n,{\tau }_{n+1}\right]$ 时，

$L_t=L_{{\tau }_n}+l(X_{{\tau }_n}^L,t-{\tau }_n^{}),$

4) 方程

${\phi }_x^l\left(t\right)=x+{\displaystyle {\int }_0^{t}g\left({\phi }_x^l\left(s\right)\right)\text{d}s}-l\left(x,t\right)$ (4.1)

有唯一解 ${\phi }^l$ ；

通过上述定义及 [10] 定理2.3可得集合 $M$ 中的函数是马氏策略函数。

引理4.2：假设存在最优平稳马氏策略 $L^{*}$ 及相应的函数 $l^{*}\in M$ 。值函数V满足

$V\left(x\right)=\underset{l\in M}{\sup }{E}_x\left[{\displaystyle {\int }_0^{t\wedge {\tau }_1}{e}^{-\delta t}l\left(x,\text{d}s\right)+{\text{e}}^{-\delta \left(t\wedge {\tau }_1\right)}V\left(X_{t\wedge {\tau }_1}^L\right)}\right],x\ge 0,t\ge 0$ (4.2)

其中 $X_{t\wedge {\tau }_1}^L={\phi }_x^l\left(t\wedge {\tau }_1^l\right)-Y_1{I}_{\left\{{\tau }_1\le t\right\}}$ 。

证明：当最优策略 $L^{*}$ 是平稳马氏策略时，可得

$V\left(x\right)=E_x\left[{\displaystyle {\int }_0^{t\wedge {\tau }_1}{e}^{-\delta s}{l}^{*}\left(x,\text{d}s\right)}\right]+E_x\left[{\displaystyle {\int }_{t\wedge {\tau }_1}^{{\tau }^{L^{*}}}{e}^{-\delta s}\text{d}{L}_s^{*}}\right],t\ge 0,x\ge 0$ (4.3)

由于 $L^{*}$ 是马氏策略，则等式右边第二部分可以写成

$E_x\left[{\displaystyle {\int }_{t\wedge {\tau }_1}^{{\tau }^{L^{*}}}{e}^{-\delta s}\text{d}{L}_s^{*}}\right]=E\left[{\text{e}}^{-\delta \left(t\wedge {\tau }_1\right)}V\left(X_{{}_{t\wedge {\tau }_1}}^{L^{*}}\right)\right].$

则(4.3)可写为

$V\left(x\right)=E_x\left[{\displaystyle {\int }_0^{t\wedge {\tau }_1}{e}^{-\delta s}{l}^{*}\left(x,\text{d}s\right)}+{\text{e}}^{-\delta \left(t\wedge {\tau }_1\right)}V\left(X_{t\wedge {\tau }_1}^{L^{*}}\right)\right],$ $x\ge 0,t\ge 0$ (4.4)

函数 $l\in M$ 。下面我们构造一个新的策略L：将

分红策略在第一次索赔到达前为一般策略L，在之后的索赔到达间隔之间为最优策略 $L^{*}$ 。

在新的策略之下，值函数满足

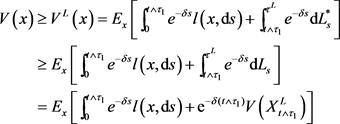(4.6)

由(4.4)和(4.6)，可得(4.2)。

定理4.3：假设存在最优平稳马氏策略 $L^{*}\in {\Pi }_x$ 及函数 $l^{*}\in M$ ，则值函数V(x)满足

$0=\underset{l\in M}{\sup }\left\{l\left(x,t\right)-\delta {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s+A^{l}V\left(x,t\right)}\right\},$ (4.7)

其中

$\begin{array}{c}{A}^{l}V\left(x,t\right)=V\left(\phi \left(t\right)\right)-V\left(x\right)-\lambda {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s}\\ +\lambda {\displaystyle {\int }_0^t{\displaystyle {\int }_0^{{\phi }_x^l\left(s\right)}V\left({\phi }_x^l\left(s\right)-y\right)\text{d}Q\left(y\right)\text{d}s.}}\end{array}$

根据引理3.1, 有

$\begin{array}{c}V\left(x\right)\ge E_x\left[{\displaystyle {\int }_0^{t\wedge {\tau }_1}{e}^{-\delta s}l\left(x,\text{d}s\right)}+e^{-\delta \left(t\wedge {\tau }_1\right)}V\left(X_{t\wedge {\tau }_1}^L\right)\right]\\ =F\left(x,t\right){\displaystyle {\int }_0^{t\wedge {\tau }_1}{e}^{-\delta s}l\left(x,\text{d}s\right)}+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^s{e}^{-\delta u}l\left(x,\text{d}u\right)}}\text{d}F\left(x,s\right)\\ +F\left(x,t\right)e^{-\delta t}V\left({\phi }_x^l\left(t\right)\right)+{\displaystyle {\int }_0^t{e}^{-\delta s}}{\displaystyle {\int }_0^{{\phi }_x^l\left(s\right)}V\left({\phi }_x^l\left(s\right)-y\right)}\text{d}Q\left(y\right)\text{d}F\left(x,s\right).\end{array}$

运用分部积分，得

$e^{-\lambda s}{\displaystyle {\int }_0^t{e}^{-\delta s}l\left(x,ds\right)}$

$={\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}l\left(x,ds\right)}+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^s{e}^{-\delta u}l\left(x,du\right)}}d{e}^{-\lambda s}$

和

$\begin{array}{l}{e}^{-\lambda t}{e}^{-\delta t}V\left({\phi }_x^l\left(t\right)\right)\\ =V\left(x\right)+{\displaystyle {\int }_0^t{e}^{-\delta s}V\left({\phi }_x^l\left(s\right)\right)d{e}^{-\lambda s}}+{\displaystyle {\int }_0^t{e}^{-\lambda s}{e}^{-\delta s}dV\left({\phi }_x^l\left(s\right)\right)}\\ -\delta {\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}V\left({\phi }_x^l\left(s\right)\right)}ds.\end{array}$

则

$\begin{array}{l}0\ge {\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}\left[-\left(\lambda +\delta \right)V\left({\phi }_x^l\left(s\right)\right)+\lambda {\displaystyle {\int }_0^{{\phi }_x^l\left(s\right)}V\left({\phi }_x^l\left(s\right)-y\right)dQ\left(y\right)}\right]}ds\\ +{\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}l\left(x,ds\right)}+{\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}dV\left({\phi }_x^l\left(s\right)\right)}\end{array}$ (4.8)

令

$H^{l}V\left(x,t\right)={\displaystyle {\int }_0^t[-\left(\lambda +\delta \right)V\left({\phi }_x^l\left(s\right)\right)}+\lambda {\displaystyle {\int }_0^{{\phi }_x^l\left(s\right)}V\left({\phi }_x^l\left(s\right)-y\right)dQ\left(y\right)}]ds+l\left(x,t\right)+V\left({\phi }_x^l\left(t\right)\right)-V(x)$

方程(4.8)可写为

$\begin{array}{l}0\ge {\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}{H}^{l}V\left(x,ds\right)}\\ ={\displaystyle {\int }_0^u{e}^{-\delta s}{e}^{-\lambda s}{H}^{l}V\left(x,ds\right)}+{\displaystyle {\int }_u^t{e}^{-\delta s}{e}^{-\lambda s}{H}^{l}V\left(x,ds\right)}\end{array}$ 。

$l\in M$ ，根据 [10] 定理2.3知： ${\phi }_x^l\left(s+t\right)={\phi }_{{\phi }_x^l\left(s\right)}^l\left(t\right)$ ，则有

$H^{l}V\left(x,0\right)=0$ ， $H^{l}V\left(x,s+t\right)=H^{l}V\left(x,s\right)+H^{l}V\left({\phi }_x^l\left(s\right),t\right)$ 。

因此

${\displaystyle {\int }_u^t{e}^{-\delta s}{e}^{-\lambda s}{H}^{l}V\left(x,ds\right)}={\displaystyle {\int }_0^{t-u}{\text{e}}^{-\delta \left(u+s\right)}{\text{e}}^{-\lambda \left(u+s\right)}{H}^{l}V\left({\phi }_x^l\left(u\right),ds\right)}\le 0$ 。

由上可得 ${\displaystyle {\int }_0^t{e}^{-\delta s}{e}^{-\lambda s}{H}^{l}V}\left(x,\text{d}s\right)$ 关于t是非增的。对于任意 $x\ge 0$ ，可得

$0\ge l\left(x,t\right)-\delta {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s}+A^{l}V\left(x,t\right)$ ， (4.9)

其中

$\begin{array}{c}{A}^{l}V\left(x,t\right)=V\left(\phi \left(t\right)\right)-V\left(x\right)-\lambda {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s}\\ +\lambda {\displaystyle {\int }_0^t{\displaystyle {\int }_0^{{\phi }_x^l\left(s\right)}V\left({\phi }_x^l\left(s\right)-y\right)dQ\left(y\right)\text{d}s.}}\end{array}$

另一方面，假设存在最优平稳马氏策略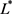及相应的函数 $l^{*}\in M$ 。运用与(4.9)相同的推导方法，(4.3)可写为

$0=l^{*}\left(x,t\right)-\delta {\displaystyle {\int }_0^{t}V\left({\phi }_x^{l^{*}}\left(s\right)\right)\text{d}s+A^{l}V\left(x,t\right)}$ (4.10)

由(4.9)和(4.10)，可得

$0=\underset{l\in M}{\sup }\left\{l\left(x,t\right)-\delta {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s+A^{l}V\left(x,t\right)}\right\}$ 。

对固定的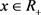，上述等式在 $l\in M$ 时取得最大值等价于 $l\left(x,\cdot \right)\in U_x$ 时取最大值。我们可改写(4.7)，如下式：

$$ (4.11)

其中

$\begin{array}{c}{A}^{l}V\left(x,t\right)=V\left(\phi \left(t\right)\right)-V\left(x\right)-\lambda {\displaystyle {\int }_0^{t}V\left({\phi }_x^l\left(s\right)\right)\text{d}s}\\ +\lambda {\displaystyle {\int }_0^t{\displaystyle {\int }_0^{{\phi }_x^l(s)}V\left({\phi }_x^l\left(s\right)-y\right)\text{d}Q\left(y\right)\text{d}s.}}\end{array}$

方程(4.11)是测度值方程，因此我们可以称之为测度值动态规划方程(测度值DPE)。