1. 引言
石墨烯衍生物,如石墨烯薄片,因其比表面积大,界面粘附性强以及其出色的电学、光学、力学性能,被广泛用作聚合物和金属基体中的增强体。Rafiee等人 [1] 指出,在纯环氧树脂梁中加入0.1%体积含量的石墨烯填充物,石墨烯/环氧树脂复合材料梁的屈曲载荷与纯环氧树脂相比增加达52%。Parashar等人 [2] 通过有限元方法研究了石墨烯/环氧树脂板的屈曲行为。他们观察到石墨烯/环氧树脂板的屈曲载荷会增加26%,而石墨烯增强体的体积分数仅为6%。
由于石墨烯优异的性能,国内外许多学者针对石墨烯增强复合材料结构的力学行为做了大量的研究。杨等人 [3] 对弹性基地下梁的屈曲和后屈曲行为进行了研究,该文章借助于功能梯度材料的概念,把有若干层石墨烯片叠加而成的石墨烯小块作为有效的增强体,随机或均匀地散布在各向同性的聚合物基体中,其中石墨稀的重量分数随着层数的改变呈梯度或均匀变化,故该系统中每一层都是各向同性的。该文章为后期石墨烯增强复合材料结构的研究做了开创性的工作。在此基础上,Wang等人 [4] 利用Navier方法对功能梯度石墨烯增强复合材料扁壳的自由振动和弯曲行为进行了分析。王等人 [5] 利用多尺度方法研究了石墨烯片增强金属泡沫圆柱壳的非线性振动。基于IMLS-Ritz有限元方法,郭 [6] 等人对四边形板的自由振动特性进行了研究。基于微分求积法,毛等人 [7] 开展了石墨烯增强压电复合材料板的自由振动方面的研究。上述工作对石墨烯增强复合材料在工程中的应用以及后期研究打下了坚实的基础。
截顶圆锥壳是一种非常受欢迎的工程结构,在建筑、航空航天等领域受到诸多研究者和工程师的关注。但在公开发表的文献中,针对石墨烯增强复合材料结构力学行为的研究,仅限于梁、板、扁壳和圆柱壳,对截顶圆锥壳的研究鲜有报道。为了石墨烯增强复合材料截顶圆锥壳结构的设计和其在工程领域的进一步应用,对其力学行为进行研究是非常有必要的。
本文基于一阶剪切理论 [8] 对石墨烯增强复合材料截顶圆锥壳的自由振动进行分析。通过能量守恒和Rayleigh-Ritz方法得到该结构自由振动的固有频率,分析石墨烯不同的物性参数和几何参数对石墨烯增强复合材料截顶圆锥壳的自由振动的影响。
2. 石墨烯增强复合材料截顶圆锥壳及其物性参数
假设简单支撑边界条件下的截顶圆锥壳体(图1),其长度为L,厚度为h,两底面半径分别为
,总层数为
。石墨烯小块作为增强体在截顶圆锥壳体厚度方向上呈现如下四种分布模式:U均匀分布,O、X和A梯度分布(图2)。丰富的石墨烯对于O分布来说是集中在中间层,对X分布则是集中在壳体上下表层,A分布是自上而下越来越多。如图2所示颜色越深代表石墨烯增强体的含量越高。第k层的杨氏模量可以用修正的Halpin-Tsai模型 [3] [4] 估计如下:
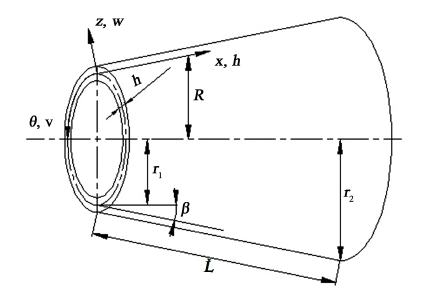
Figure 1. Geometry of truncated conical shell
图1. 截顶圆锥壳的几何示意图

Figure 2. Different graphene distribution patterns
图2. 石墨烯片的分布模式
(1)
其中
(2)
,
,
,
和
分别为基体和石墨烯的杨氏模量、石墨烯小块的长度、宽度以及厚度,第k层石墨烯体积分数计算公式如下:
(3)
是第k层石墨烯小块的质量分数,其在不同分布模式下的计算公式如下:
U:
(4)
O:
(5)
X:
(6)
A:
(7)
其中
,
是石墨烯的总质量分数,质量密度
和泊松比
用混合准则有效地表示
(8)
其中,“G”,“M”,“c”分别表示石墨烯,基体以及复合材料。
3. 位移场和本构关系方程
截顶圆锥壳进行力学分析所用的位移场如下 [8] :
(9)
其中
分别为沿
方向的全局位移和中面位移,
和
分别是绕母线和轴向的转角,线性von-Karman应变位移关系如下:
(10)
其中,
为应变向量,
为位移向量。
分别表示对空间坐标
的偏导数。
则第k 层的本构关系为
(11)
其中
为应力向量,刚度矩阵为如下形式
(12)
其中
4. 基于Rayleigh-Ritz方法固有频率的计算
根据公式(10)-(11),截顶圆锥壳的变形势能表达式如下:
(13)
动能为:
(14)
简支边界条件表达形式如下:
(15)
根据上述边界条件,该系统位移场中的未知量
可以用以下傅立叶级数表示 [9] :
(16)
其中
分别为各阶模态的振幅。
将(16)代入(13)和(14),并令
,可以得到最大变形能
,最大动能
,利用Rayleigh-Ritz方法,得到
(17)
通过公式(17)可以推导出如下方程
(18)
其中
,
分别为刚度和向量矩阵。通过求解方程(18)系数矩阵的特征值得到截顶圆锥壳体的各阶频率。
5. 数值算例
本文采用环氧树脂作为系统的基体,石墨烯小块作为增强体,若无特别说明,实验中所用的参数如下 [2] [10] :
下面将对不同石墨烯小块系统分层数、分布模式、半顶角、质量分数、底面半径与厚度比等参数对系统的自由振动行为的影响进行分析讨论。
图3展示了石墨烯增强复合材料截顶圆锥壳在不同的系统分层数下的无量纲固有频率。可以看出,截顶圆锥壳的无量纲基频对于U型分布来说,其值不变,原因在于在厚度上每层石墨烯含量是均匀一致的。对于层合板来讲,板表层对振动的影响比中间层要大。在石墨烯体积分数一定的情况下,随着分层数的增加,X型分布的层合板表层石墨烯含量逐渐增加,导致临近表层的刚度增加,从而导致其无量纲基频随着分层数的增加而增加,相反的趋势发生在分布O和A模式。另外,当系统的分层数大于20时,所有的石墨烯分布模式下系统的无量纲基频均趋于稳定。下面的数值实验中,均选取石墨烯分层数
。
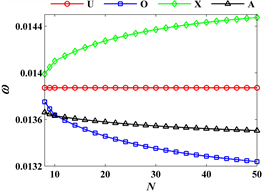
Figure 3. Dimensionless fundamental frequency of truncated conical shells based on different total layers
图3. 不同分层数下截顶圆锥壳的无量纲基频
图4给出了石墨烯增强复合材料截顶圆锥壳的无量纲基频随着半顶角变化的趋势图。可以看出,四种分布模式下系统的无量纲基频随着半顶角的增大而增大,50度达到最大值,之后无量纲基频处于递减状态。这说明系统刚度与结构的形状有着密切的关系。下面试验中固定半顶角
。
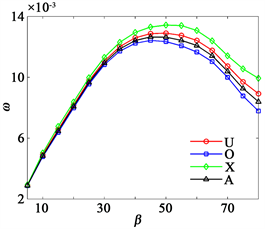
Figure 4. Dimensionless fundamental frequency of truncated conical shells based on different semivertex angles
图4. 不同半顶角下截顶圆锥壳的无量纲基频
图5给出了截顶圆锥壳的无量纲基频相对变化率随着石墨烯含量变化的趋势图。其中
表示石墨烯增强复合材料截顶圆锥壳相对于纯基体结构无量纲基频增加的相对变化率,
表示纯基体结构的无量纲基频。可以看出,截顶圆锥壳体的无量纲基频相对变化率随着石墨烯含量的增加而增加,原因在于截顶圆锥壳体随着高含量石墨烯的加入,其刚度会随之明显增大。表1给出了在石墨烯不同分布模式下截顶圆锥壳的前六阶无量纲固有频率。从表1和图5可以看出,在石墨烯含量相同的情形下,分布模式X对石墨烯增强复合材料截顶圆锥壳体的各阶无量纲固有频率影响最大,这种现象表明在石墨烯总体含量一定的情形下,把较多含量的石墨烯铺设在结构表层比分布在中间层会更加有效地提高其整体刚度,从而使得系统的固有频率增大。
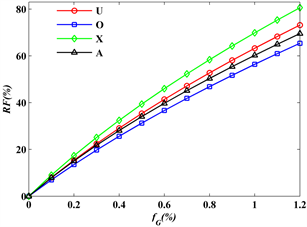
Figure 5. Variation of dimensionless fundamental frequency of truncated conical shells with graphene weight fraction
图5. 截顶圆锥壳的无量纲基频变化率随石墨烯质量分数的变化

Table 1. The first six order dimensionless natural frequencies of system under different distributions
表1. 不同分布模式下的前6阶无量纲固有频率
固定截顶圆锥壳的底面半径
,图6表明当
从50递增到200,截顶圆锥壳的无量纲基频迅速减小,之后就变得平缓,分布模式间的差异也变小。
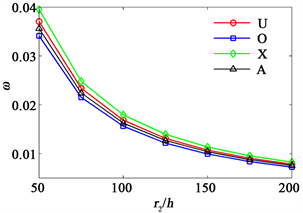
Figure 6. Dimensionless fundamental frequency of truncated conical shells based on different bottom radius-to-thickness ratios
图6. 不同底面半径与厚度比下截顶圆锥壳的无量纲基频
6. 小结
本文基于Rayleigh-Ritz方法的计算结果对石墨烯增强复合材料截顶圆锥壳的自由振动进行了不同角度的分析讨论。对于不同石墨烯分布模式下的不同截顶圆锥壳进行了多种相关参数的讨论研究。数值计算结果表明,少量的石墨烯增强体可以显著地提高结构的整体刚度从而提高其自由振动基频。在相同石墨烯含量的前提下,X分布模式比其它分布模式更能有效的提高系统的整体刚度,从而有效的改善结构的无量纲基频变化率。截顶圆锥壳体的无量纲基频也与其半顶角的大小以及底面半径与厚度的比例有关。上述研究对于石墨烯增强复合材料截顶圆锥壳结构的设计和该材料结构在工程领域的进一步应用都有着十分重要的指导意义。
基金项目
国家自然科学基金(11772063)。
NOTES
*通讯作者。