基于有限元方法的Cahn-Hilliard方程能量不变二次化数值模拟

Numerical Simulation of Energy Invariant Quadratic Cahn-Hilliard Equation Based on Finite Element Method

摘要: 文章分析了Cahn-Hilliard方程的能量不变二次化法的能量稳定性。首先分析了Cahn-Hilliard方程是满足能量耗散，即能量随时间的推移呈衰减趋势，并且这种随时间衰减的性质能得到保持。其次，对定义的自由能被积函数变换成新的二次函数，即能量不变二次化法同样验证了它的能量衰减性质，并给出了Cahn-Hilliard方程能量不变二次化法的能量稳定性。结果表明，该数值格式是无条件稳定，即能量稳定性与时间步长是无关的。最后我们基于有限元方法给出了一个数值算例，来有效的模拟Cahn-Hilliard方程相位变化情况。

Abstract: The article analyzes the energy stability of the energy-invariant quadratic method of the Cahn-Hilliard equation. Firstly, it is analyzed that the Cahn-Hilliard equation is satisfying energy dissipation, i.e., the energy tends to decay with time, and this decaying property with time can be maintained. Secondly, the defined free energy quadratic function is transformed into a new quadratic function, i.e., the energy-invariant quadratic method is similarly verified for its energy-decaying property, and the energy stability of the energy-invariant quadratic method of the Cahn-Hilliard equation is given. The results show that the numerical format is unconditionally stable, i.e. the energy stability is independent of the time step. Finally we give a numerical example based on the finite element method to effectively simulate the phase variation of the Cahn-Hilliard equation.

1. 引言

Cahn-Hilliard方程最初是由Cahn和Hilliard在文献 [1] 中介绍，用以描述熔融合金中复杂的相分离和粗化现象，该合金被淬灭到只有两个不同的浓度相可以稳定存在的温度。随着理论的发展，对Cahn-Hilliard方程的研究也受到众多学者追捧，Cahn-Hilliard方程在流体力学中具有重要应用，并被许多学者广泛研究 [2] [3] [4] [5]。Cahn-Hilliard相场方程经常用来描述油水相分离的行为，在工业上有着重要的应用。在不同的研究领域Cahn-Hilliard方程的模型也各有不同，本文要研究的Cahn-Hilliard方程模型如下 [6] [7]：

$\{\begin{array}{l}\frac{\partial u}{\partial t}+\Delta \left(\epsilon \Delta u-f\left(u\right)\right)=0,\left(x,t\right)\in \Omega x\left(0,T\right]\hfill \\ \frac{\partial u}{\partial n}=\frac{\partial \left(f\left(u\right)-\epsilon \Delta u\right)}{\partial n}=0,x\in \partial \Omega ,\underset{\underset{}{}}{\overset{\stackrel{}{}}{}}\hfill \\ u\left(x,0\right)=u_0\left(x\right),x\in \partial \Omega .\stackrel{}{}\hfill \end{array}$ (1)

在方程中u表示混合物的浓度， $\epsilon$ 是一个与界面厚有关的参数( $\epsilon >0$ )，n为边界 $\partial \text{Ω}$ 上的外法向量，其中f是光滑函数F的导数。特别地，取

$f\left(u\right)=u\left(u^2-1\right),F\left(u\right)=\frac{1}{4}{\left(u^2-1\right)}^2$

其中f需要满足：存在常数L，使得

$\underset{u\in R}{\max }\left|f^{\prime }\left(u\right)\right|\le L$

Cahn-Hilliard方程它有一个重要的性质就是可以做Liapunov能量函数 [1]

$E\left(u\right)={\displaystyle {\int }_{\Omega }\left(\frac{\epsilon }{2}{\left|\nabla u\right|}^2+F\left(u\right)\right)\text{d}x}$

$E\left(u\right)$ 称作自由能泛函，它能准确的表述混合物的自由能。

2. Cahn-Hilliard方程的能量耗散性

2.1. 能量耗散

本文要研究的稳定性Cahn-Hilliard方程能量稳定的 [8]，给出下面的引理

引理1 Cahn-Hilliard方程定义的自由能 $E\left(u\right)$ 满足下面的定律

$\frac{\partial }{\partial t}E\left(u\left(t\right)\right)=-{\displaystyle {\int }_{\Omega }{\left|\nabla \left(\epsilon \Delta u-f\left(u\right)\right)\right|}^2\text{d}}x\le 0$

即Cahn-Hilliard方程是满足能量耗散的。

证明 取 $\vartheta$ 与(1)式的第一个式子做内积，有

$\left(u_t,\vartheta \right)=\left(\Delta \left(f\left(u\right)-\epsilon \Delta u\right)u,\vartheta \right)$

式中 $u_t=\frac{\partial u}{\partial t}$， $\left(\cdot ,\cdot \right)$ 表示内积。取 $\vartheta =f\left(u\right)-\epsilon \Delta u$

$\left(u\left(t\right),f\left(u\right)-\epsilon \Delta u\right)=\left(\Delta \left(f\left(u\right)-\epsilon \Delta u\right),f\left(u\right)-\epsilon \Delta u\right)$

由格林公式以及边界条件可得

$\epsilon \left(\nabla u_t,\nabla u\right)+\left(u_t,f\left(u\right)\right)=-\left(\nabla \left(f(u\right)-\epsilon \Delta u\right),\nabla \left(f\left(u\right)-\epsilon \Delta u\right)$

即

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\Omega }\frac{\epsilon }{2}}{\left|\nabla u\right|}^2\text{d}x+\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\Omega }F\left(u\right)\text{d}x}=-{\displaystyle {\int }_{\Omega }{\left|\nabla \left(f\left(u\right)-\epsilon \Delta u\right)\right|}^2\text{d}x}\le 0\frac{\text{d}}{\text{d}t}E\left(u\left(t\right)\right)\\ =-{{\displaystyle {\int }_{\Omega }\left|\nabla \left(f\left(u\right)-\epsilon \Delta u\right)\right|}}^2\text{d}x\le 0\end{array}$

证毕。

2.2. 能量不变二化法

为了构造线性数值格式，我们令(1)式中 $f\left(u\right)-\epsilon \Delta u=\omega$ 的，Cahn-Hilliard方程变形为 [9]

$\{\begin{array}{l}\frac{\partial u}{\partial t}-\Delta \omega =0,f\left(u\right)-\epsilon \Delta u=\omega \left(x,t\right)\in x\left(0,T\right]\hfill \\ \frac{\partial u}{\partial n}=\frac{\partial \omega }{\partial n}=0,x\in \partial \Omega ,\underset{\underset{}{\underset{}{}}}{\overset{\stackrel{}{}}{}}\hfill \\ u\left(x,0\right)=u_0\left(x\right),x\in \partial \Omega .\hfill \end{array}$ (2)

接下来我们采用能量不变二化法来分析变换后是否满足能量耗散规律。

引理2 Cahn-Hilliard方程采用能量不变二化法后定义的自由能 $E\left(u,\delta \right)$ 满足下面的定律

$\frac{\partial }{\partial t}E\left(u,\delta \left(u\right)\right)\le 0$

即Cahn-Hilliard方程采用能量不变二化法也是满足能量耗散的。

证明 为了采用能量不变二化法，我们作以下标记：

$\delta \left(u\right)=\sqrt{F\left(u\right)+\beta },g\left(u\right)=2\frac{\text{d}}{\text{d}u}\delta \left(u\right)=\frac{f\left(u\right)}{\sqrt{F\left(u\right)+\beta }}$

则(2)式变形为

$\{\begin{array}{l}{u}_t=\Delta \omega ,\underset{}{}\hfill \\ \omega =-\epsilon \Delta u+\delta \left(u\right)g\left(u\right),\hfill \\ {\delta }_t=\frac{1}{2}g\left(u\right)u_t\text{.}\hfill \end{array}$ (3)

用(3)式中三个式子分别与 $\omega 、u_t、2\delta$ 作内积可得

$\frac{\text{d}}{\text{d}t}E\left(u,\delta \right)=-{\displaystyle {\int }_{\Omega }{\left|\nabla \omega \right|}^2\text{d}x}\le 0,$

所以我们采用能量不变二分法满足能量耗散，其中 $E\left(u,\delta \right)={\displaystyle {\int }_{\Omega }\left(\frac{\epsilon }{2}{\left|\nabla u\right|}^2+{\delta }^2\right)\text{d}x}$，这里的 $E\left(u,\delta \right)$ 和 $E\left(u\right)$ 是等价的。

3. 稳定性分析

利用格林公式和边界条件，很容易得到Cahn-Hilliard方程的变分形式 [10] [11] [12] 为：求 $\left(u,\omega \right)\in H^1\left(\Omega \right)\times H^1\left(\Omega \right)$，使得下面的式子成立

$\{\begin{array}{l}\left(u_t,v\right)+\left(\nabla \omega ,\nabla u\right)=0,\forall v\in H^1\left(\Omega \right)\hfill \\ \epsilon \left(\nabla u,\nabla \psi \right)+\left(g\left(u\right)\delta \left(u\right),\psi \right)=\left(\omega ,\psi \right),\forall \psi \in H^1(\; \Omega \; )\hfill \end{array}$

针对上面的变分形式，构造时间方向的半离散格式

$\{\begin{array}{l}\frac{1}{\tau }\left(u^{n+1}-u^n,v\right)+\left(\nabla {\omega }^{n+1},\nabla u\right)=0,\hfill \\ \epsilon \left(\nabla u^{n+1},\nabla \psi \right)+\left(g\left(u^{n+1}\right)\frac{{\delta }^{n+2}+{\delta }^n}{2},\psi \right)=\left({\omega }^{n+1},\psi \right)\text{.}\hfill \end{array}$ (4)

其中τ为时间步长,且该格式满足下面的能量估计式成立：

定理 (能量稳定性)方程(4)的解满足下面的能量稳定，即

$E\left(u^{n+1},{\delta }^{n+1}\right)-E\left(u^n,{\delta }^n\right)=-\tau {\Vert \nabla {\omega }^{n+1}\Vert }^2-\frac{\epsilon }{2}{\Vert \nabla \left(u^{n+1}-u^n\right)\Vert }^2$

其中， $E\left(u^n,{\delta }^n\right)=\frac{\epsilon }{2}{\Vert \nabla u^n\Vert }^2+\frac{1}{2}\left({\Vert {\delta }^{n+1}\Vert }^2+{\Vert {\delta }^n\Vert }^2\right)$

证明 在(4)式中取 $v=\tau {\omega }^{n+1}$， $\psi =u^{n+1}-u^n$ 有

$\{\begin{array}{l}\left(u^{n+1}-u^n,{\omega }^{n+1}\right)+\tau {\Vert \nabla {\omega }^{n+1}\Vert }^2=0,\\ \frac{\epsilon }{2}\left({\Vert \nabla u^{n+1}\Vert }^2-{\Vert \nabla u^n\Vert }^2+{\Vert \nabla \left(u^{n+1}-u^n\right)\Vert }^2\right)+\left(g\left(u^{n+1}\right)\frac{{\delta }^{n+2}+{\delta }^n}{2},u^{n+1}-u^n\right)=\left({\omega }^{n+1},u^{n+1}-u^n\right)\end{array}$ (5)

再把方程(3)中的第三式与 $2\tau \left({\delta }^{n+2}+{\delta }^n\right)$ 作内积可得

${\Vert {\delta }^{n+2}\Vert }^2-{\Vert {\delta }^n\Vert }^2=\left(g\left(u^{n+1}\right)\frac{\left(u^{n+1}-u^n\right)}{2},{\delta }^{n+2}+{\delta }^n\right)$ (6)

综合(5)、(6)两式有

$\tau {\Vert \nabla {\omega }^{n+1}\Vert }^2+\frac{\epsilon }{2}\left({\Vert \nabla u^{n+1}\Vert }^2-{\Vert \nabla u^n\Vert }^2+{\Vert \nabla \left(u^{n+1}-u^n\right)\Vert }^2\right)+{\Vert {\delta }^{n+2}\Vert }^2-{\Vert {\delta }^n\Vert }^2=0$

整理可得该定理的结果。

证毕。

4. 数值实验

为了能够有效观测Cahn-Hilliard方程相场模型的相位变化情况，采用混合有限元方法给出一个数值算例，选取精确解为

$u={\text{e}}^{-t}{\sin }^2\left(\pi x\right){\sin }^2\left(\pi y\right),\delta \left(u\right)=\frac{1}{2}\left(u^2-1\right)$

计算区域为方形区域 $\Omega ={\left(0,1\right)}^2$，其中网格尺寸选择1/64， $\tau =1.0\text{e}-6$。

图1描绘了在 $\epsilon =0.01$ 时，T = 1。0e−5，T = 1。0e−4，T = 1。0e−3，T = 1。0e−2时的相位变化图。

图2描绘了在 $\epsilon =0.1$ 时，T = 1。0e−5，T = 1。0e−4，T = 1。0e−3，T = 1。0e−2时的相位变化图。

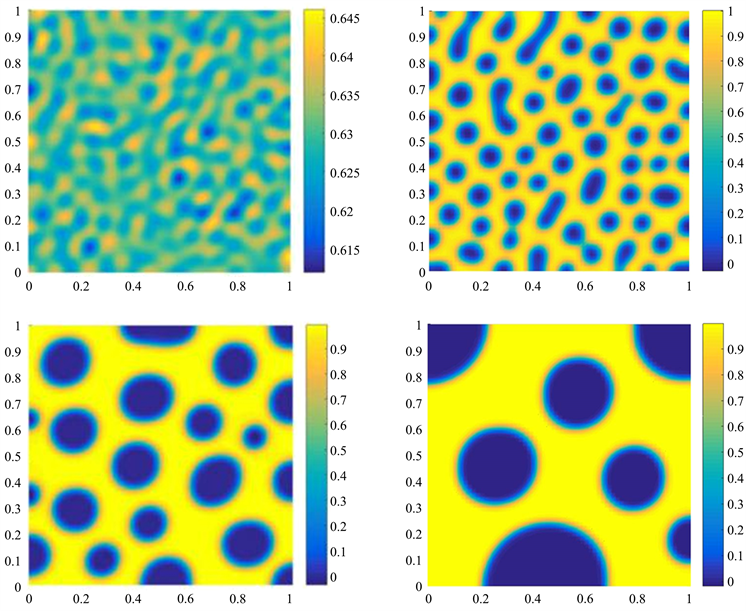
Figure 1. When ε = 0.01, the image of the change in the numerical solution u at different moments

图1. 当ε = 0.01时, 数值解u在不同时刻的变化图像

Figure 2. When ε = 0.1, the image of the change in the numerical solution u at different moments

图2. 当ε = 0.01时，数值解u在不同时刻的变化图像

从上面两图可以看到，所构造的数值算例有效的模拟了Cahn-Hilliard方程的相位变化过程，起初两种物质任意分布，随着时间的推移，两种物质逐渐趋于缓和，最后到达一种稳定状态。

比较图1和图2可以发现，当ε取不同值时，对两种物质的反应速率有很大影响，ε越小反应越剧烈，反应速率越快，相当于起到了催化剂的作用。