求解单调变分不等式问题的修正惯性次梯度外梯度算法

A Modified Inertial Subgradient Extragradient Algorithm for Solving Monotone Variational Inequality Problems

摘要: 本文提出了一种修正的惯性次梯度外梯度算法，用以求解实Hilbert空间中的具有Lipschitz连续和单调的变分不等式问题。我们在惯性次梯度外梯度算法的基础上，结合粘度逼近法，构造了一种具有强收敛性的算法。

Abstract: In this paper, a modified inertial subgradient extragradient algorithm is proposed for solving the Lipschitz-continuum and monotone variational inequality problems in real Hilbert space. On the basis of the inertial subgradient extragradient algorithm and the viscosity approximation method, we construct an algorithm with strong convergence.

1. 引言

令 $H$ 为一个实Hilbert空间， $\langle \cdot ,\cdot \rangle$ 和 $\Vert \cdot \Vert$ 分别表示 $H$ 中的内积和诱导范数， $C\subset H$ 是非空闭凸子集。令 $A:H\to H$ 为单调映射，变分不等式问题就是找到一点 $x^{\ast }\in C$，满足不等式

$\langle A{x}^{*},x-x^{*}\rangle \ge 0,\forall x\in C$

我们把上式称为单调变分不等式，其解集用 $VI\left(C,A\right)$ 表示。

变分不等式(Variational Inequalities)具有非常广泛的应用背景，是在1966年首次被Hartman和Stampacchia [1] 提出的，从被提出以来就被学者们经常应用于最优化领域中，是研究工程力学、物理、经济学、优化理论和应用科学的重要工具。从二十世纪六十年代开始至今，怎么求解变分不等式问题已经成为许多学者的研究方向，其理论和方法已经被国内外许多专家所研究。

投影算法及其变形形式为我们寻找变分不等式的近似解提供了重要的工具，投影算法的迭代格式为：

$x_{n+1}=P_C\left(x_n-\tau A{x}_n\right)$

其中 $\tau >0$ 表示步长， $P_C(\cdot )$ 表示到非空凸集 $C$ 上的投影，即：

$P_C\left(x\right)=Arg\min \left\{\Vert x-y\Vert |y\in C\right\}$

那么有： $\Vert x-P_C\left(x\right)\Vert \le \Vert x-y\Vert$ 成立。

因为基本投影算法的条件较强，它需要映射 $A$ 为Lipschitz连续和强单调的，所以为了减弱条件，Korpelevich [2] 就基于 $n$ 维欧式空间 $R^n$ 中提出了外梯度算法，受到了许多学者的关注( [3] [4] [5] )，其迭代格式为：

$\begin{array}{l}{y}_n=P_C\left(x_n-\tau A{x}_n\right)\\ x_{n+1}=P_C\left(x_n-\tau A{y}_n\right)\end{array}$

其中 $\tau \in \left(0,1/L\right)$， $L$ 为Lipschitz常数，它只需要映射 $A$ 是Lipschitz连续和一般单调的。Nadezhkina和Takahashi [6] 把外梯度方法推广到了无穷维的Hilbert空间。

又因为外梯度方法要计算两个到非空闭凸集 $C$ 上的正交投影，这两个投影在一般情况下比较难计算，所以为了克服这个困难，Censor [7] 就对外梯度算法进行了扩展，称为次梯度外梯度算法：

$\begin{array}{l}{y}_n=P_C\left(x_n-\tau A{x}_n\right)\\ x_{n+1}=P_{T_n}\left(x_n-\tau A{y}_n\right)\end{array}$

其中： $T_n:=\left\{w\in R^n|\langle \left(x_n-\tau A{x}_n\right)-y_n,w-y_n\rangle \le 0\right\}$ 该名称源于将外梯度算法中 $C$ 上的第二个正交投影替换为一个特定的次梯度投影，即构造一个特殊的半空间 $T_n$ (详细见 [7] )，把第二个正交投影的投影平面改为 $T_n$，这就避免了每次向非空闭凸集作投影的困难。后来Censor [8] 又把该算法推广到了Hilbert空间。因为次梯度外梯度算法的计算量大大减少了，所以有许多学者对其进行了改进( [9] [10] [11] )。

到了后来，为了加快算法的收敛速度，人们在原有算法的基础上加入了惯性算法，它是基于二阶动力系统在时间上的重球法 [12] [13] [14]，并且在没有惯性效应的情况下加快了原算法的收敛速度。Alvarez和Attouch [13] 应用惯性技术，得到了一种用于求解极大单调算子零点问题的惯性近端方法，其主要工作如下：令 $x_{n-1},x_n\in H$， ${\theta }_n\in \left[0,1\right)$， ${\lambda }_n>0$，找到点 $x_{n+1}\in H$，使得：

$0\in {\lambda }_{n}A\left(x_{n+1}\right)+x_{n+1}-x_n-{\theta }_n\left(x_n-x_{n-1}\right)$

上式可以等价地写成如下形式：

$x_{n+1}=J_{{\lambda }_n}^A\left(x_n+{\theta }_n\left(x_n-x_{n-1}\right)\right)$

其中 $J_{{\lambda }_n}^A$ 是参数 ${\lambda }_n$ 在 $A$ 上的解，而惯性是由 ${\theta }_n\left(x_n-x_{n-1}\right)$ 引起的。

Duong和Dang [15] 就在Censor [8] 和Alvarez [13] 的启发下，结合惯性技术和次梯度外梯度算法提出了一种惯性次梯度外梯度算法，并创建了算法的弱收敛性，算法迭代格式为：

选择点 $x_0,x_1\in H$，计算

$\begin{array}{l}{w}_n=x_n+{\alpha }_n\left(x_n-x_{n-1}\right)\\ y_n=P_C\left(w_n-\tau A{w}_n\right)\\ T_n=\left\{x\in H|\langle w_n-\tau A{w}_n-y_n，x-y_n\rangle \le 0\right\}\\ x_{n+1}=P_{T_n}\left(w_n-\tau A{y}_n\right)\end{array}$

其中 $\tau >0$， ${\alpha }_n\ge 0$。

粘度逼近法 [16] 是求非扩张自映射 $P$ 的不动点的一种方法，即要找到一点 $x*$，使得 $x*=P\left(x*\right)$，其迭代格式为：选取迭代点 $x_n$，计算：

$x_{n+1}=\theta P\left(x_n\right)+\left(1-\theta \right)f(\; x\; n\; )$

其中 $f:H\to C$ 为一个压缩映射，文章证明了迭代序列 $\left\{x_n\right\}$ 强收敛于 $x*$。

本文在惯性次梯度外梯度算法的基础上，结合并运用两次粘度逼近法，提出了一种用于求解单调变分不等式的修正惯性次梯度外梯度算法，本文提出的算法提高了原算法的收敛性，并证明了由算法生成的序列强收敛于一个特定的解。

2. 预备知识

令 $H$ 为一个实Hilbert空间， $\langle \cdot ,\cdot \rangle$ 表示为 $H$ 中的内积， $\Vert \cdot \Vert$ 表示为 $H$ 中的诱导范数， $C\subset H$ 是非空闭凸子集。 $\left\{x_n\right\}$ 强收敛到 $x$，记为 $x_n\to x\left(n\to \infty \right)$ ； $\left\{x_n\right\}$ 弱收敛到 $x$，记为 $x_n\rightharpoonup x\left(n\to \infty \right)$。

对 $\forall x,y\in H$ 和 $\alpha \in R$，有：

${\Vert \alpha x+\left(1-\alpha \right)y\Vert }^2=a{\Vert x\Vert }^2+\left(1-\alpha \right){\Vert y\Vert }^2-a\left(1-\alpha \right)\Vert x-y\Vert$ (1)

${\Vert x+y\Vert }^2\le {\Vert x\Vert }^2+2\langle y,x+y\rangle$ (2)

命题2.1设 $\alpha ,\beta \in R$，对任意的 $x,y,z\in H$，有

${\Vert \left(1-\alpha \right)x+\alpha \left[\left(1-\beta \right)y+\beta z\right]\Vert }^2\le \left(1-\alpha \right){\Vert x\Vert }^2+\alpha \left(1-\beta \right){\Vert y\Vert }^2+\alpha \beta {\Vert z\Vert }^2$

证明：使用两次(1)式，得

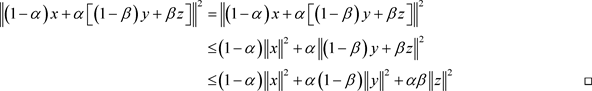
引理2.1 [17] 设 $C\subset H$ 是闭凸集，则对 $\forall x\in H$，有

(1) ${\Vert P_C\left(x\right)-P_C\left(y\right)\Vert }^2\le \langle P_C\left(x\right)-P_C\left(y\right),x-y\rangle ,\forall y\in H$

(2) ${\Vert P_C\left(x\right)-y\Vert }^2\le {\Vert x-y\Vert }^2-{\Vert x-P_C\left(x\right)\Vert }^2,\forall y\in H$

(3) $z=P_C\left(x\right)\iff \langle x-z,z-y\rangle \ge 0,\forall y\in C$

定义2.1令 $T:H\to H$ 是一个映射，对 $\forall x,y\in H$，有

(1) 若存在常数 $L>0$，有下面式子成立，则称映射 $T$ 是Lipschitz连续的

$\Vert T\left(x\right)-T\left(y\right)\Vert \le L\Vert x-y\Vert$

(2) 若有下面式子成立，则称映射 $T$ 是单调的

$\langle T\left(x\right)-T\left(y\right),x-y\rangle \ge 0$

引理2.2 [18] 设 $\Omega$ 是Hilbert空间中 $H$ 上的一个闭凸集， $A:H\to H$ 是 $\Omega$ 上的一个单调且Lipschitz连续的

映射， $VI\left(\Omega ,A\right)\ne \varnothing$ 且 $\tau$ 为一个正实数，使得 $\tau \in \left(0,\frac{1}{L}\right)$。令 $\left\{x_n\right\}\subset H$ 定义为：

$\begin{array}{l}{x}_0\in H\\ y_n=P_{\Omega }\left(x_n-\tau A{x}_n\right)\\ T_n=\left\{x\in H:\langle x_n-\tau A{x}_n-y_n,x-y_n\rangle \le 0\right\}\\ z_n=P_{T_n}\left(x_n-\tau A{y}_n\right)\end{array}$

那么，对 $\forall p\in VI\left(\Omega ,A\right)$，我们有：

${\Vert z_n-p\Vert }^2\le {\Vert x_n-p\Vert }^2-\left(1-\tau L\right){\Vert y_n-x_n\Vert }^2-\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2$

3. 修正的惯性次梯度外梯度方法

设 $A:H\to H$ 为一个在 $H$ 上单调且Lipschitz连续的映射， $VI\left(\Omega ,A\right)\ne \varnothing$。 $f:H\to H$ 是一个压缩映射，压缩系数为 $\kappa \in \left[0,1\right)$。

算法3.1 (修正的惯性次梯度外梯度算法)：

Step 0 (初始化)：设置 $\tau \in \left(0,\frac{1}{L}\right),\left\{{\alpha }_n\right\}\subset \left[0,\alpha \right)$ 其中 $\alpha >0$， $\left\{{\beta }_n\right\}\subset \left(0,1\right)$， $\left\{{\theta }_n\right\}\subset \left(\tilde{\theta },1\right]$， $0<\tilde{\theta }<1$，满足

以下条件：

$\underset{n\to \infty }{\lim }{\beta }_n=0,{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}{\beta }_n=\infty }$

设置初始点 $x_0,x_1\in C$ 和 $n:=1$。

Step 1：计算：

$\begin{array}{l}{w}_n=x_n+{\alpha }_n\left(x_n-x_{n-1}\right)\\ y_n=P_C\left(w_n-\tau A{w}_n\right)\end{array}$

如果 $y_n=w_n$，迭代停止( $y_n$ 即为变分不等式的解)。否则进行Step 2。

Step 2：构造半空间：

$T_n=\left\{z\in R^n\langle w_n-\tau A{w}_n-y_n,z-y_n\rangle |\le 0\right\}$

计算： $z_n=P_{T_n}\left(w_n-\tau A{y}_n\right)$。

Step 3：计算：

$x_{n+1}=\left(1-{\theta }_n\right)x_n+{\theta }_n\left[\left(1-{\beta }_n\right)z_n+{\beta }_{n}f\left(z_n\right)\right]$

令 $n:=n+1$，回到Step 1。

定理3.1：假设序列 $\left\{{\alpha }_n\right\}$ 使得

$\underset{n\to \infty }{\lim }\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert =0$ (3)

由算法生成的序列 $\left\{x_n\right\}$ 收敛于 $p\in VI\left(C,A\right)$，其中 $p=P_{VI\left(C,A\right)}°f\left(p\right)$。

要证明这个定理，我们首先证明以下几个引理：

引理3.1 由算法生成的序列 $\left\{x_n\right\}$ 都是有界的。

证明：因为 $p\in VI\left(C,A\right)$，通过引理2.2，我们有：

${\Vert z_n-p\Vert }^2\le {\Vert w_n-p\Vert }^2-\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2-\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2$ (4)

即有：

$\Vert z_n-p\Vert \le \Vert w_n-p\Vert$ (5)

通过 $w_n$ 的定义得：

$\begin{array}{c}\Vert w_n-p\Vert =\Vert x_n+{\alpha }_n\left(x_n-x_{n-1}\right)-p\Vert \le \Vert x_n-p\Vert +{\alpha }_n\Vert x_n-x_{n-1}\Vert \\ =\Vert x_n-p\Vert +{\beta }_n\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert \end{array}$ (6)

又因为 $\underset{n\to \infty }{\lim }\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert =0$，所以存在常数 $M_1\ge 0$，对任意的 $n\ge 0$，使得

$\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert \le M_1$ (7)

结合(5)、(6)和(7)式，我们得到：

$\Vert z_n-p\Vert \le \Vert w_n-p\Vert \le \Vert x_n-p\Vert +{\beta }_n{M}_1$ (8)

通过 $x_{n+1}$ 和 $f$ 的定义可得：

$\begin{array}{c}\Vert x_{n+1}-p\Vert =\Vert \left(1-{\theta }_n\right)\left(x_n-p\right)+{\theta }_n\left[\left(1-{\beta }_n\right)\left(z_n-p\right)+{\beta }_n\left(f\left(z_n\right)-p\right)\right]\Vert \\ \le \left(1-{\theta }_n\right)\Vert x_n-p\Vert +{\theta }_n\left(1-{\beta }_n\right)\Vert z_n-p\Vert \\ +{\theta }_n{\beta }_n\Vert f\left(z_n\right)-f\left(p\right)\Vert +{\theta }_n{\beta }_n\Vert f\left(p\right)-p\Vert \\ \le \left(1-{\theta }_n\right)\Vert x_n-p\Vert +{\theta }_n\left(1-\left(1-\kappa \right){\beta }_n\right)\Vert z_n-p\Vert +{\theta }_n{\beta }_n\Vert f\left(p\right)-p\Vert \end{array}$ (9)

把(8)代入(9)式，得到：

$\begin{array}{c}\Vert x_{n+1}-p\Vert \le \left(1-{\theta }_n\right)\Vert x_n-p\Vert +{\theta }_n\left(1-\left(1-\kappa \right){\beta }_n\right)\Vert x_n-p\Vert +{\theta }_n{\beta }_n{M}_1+{\theta }_n{\beta }_n\Vert f\left(p\right)-p\Vert \\ =\left(1-\left(1-\kappa \right){\theta }_n{\beta }_n\right)\Vert x_n-p\Vert +\left(1-\kappa \right){\theta }_n{\beta }_n\frac{\left(M_1+\Vert f\left(p\right)-p\Vert \right)}{1-\kappa }\\ \le \max \left\{\Vert x_n-p\Vert ,\frac{M_1+\Vert f\left(p\right)-p\Vert }{1-\kappa }\right\}\\ \le \cdots \\ \le \max \left\{\Vert x_0-p\Vert ,\frac{M_1+\Vert f\left(p\right)-p\Vert }{1-\kappa }\right\}\end{array}$ (10)

由此可以推出 $\left\{x_n\right\}$ 有界，也可以顺便推出 $\left\{z_n\right\},\left\{f\left(z_n\right)\right\},\left\{w_n\right\}$ 有界。 □

引理3.2 对于由算法生成的序列 $\left\{x_n\right\},\left\{y_n\right\},\left\{z_n\right\},\left\{w_n\right\}$，以及 $p\in VI\left(C,A\right)$，有以下不等式成立：

${\theta }_n\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2+{\theta }_n\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2\le {\Vert x_n-p\Vert }^2-{\Vert x_{n+1}-p\Vert }^2+{\beta }_n{M}_4$

其中： $M_2:=2\Vert f\left(p\right)-p\Vert \underset{n\in \mathbb{N}}{\sup }\left\{\Vert z_n-p\Vert \right\}+{\Vert f\left(p\right)-p\Vert }^2$

$M_3:=\underset{n\in \mathbb{N}}{\sup }\left\{2M_1\Vert x_n-p\Vert +{\beta }_n{M}_1^2\right\}$

$M_4:=M_2+M_3$

证明：

由 $x_{n+1}$ 的定义和命题2.1，得到：

$\begin{array}{l}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n\left(1-{\beta }_n\right){\Vert z_n-p\Vert }^2+{\theta }_n{\beta }_n{\Vert f\left(z_n\right)-p\Vert }^2\\ \le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n\left(1-{\beta }_n\right){\Vert z_n-p\Vert }^2+{\theta }_n{\beta }_n{\left(\Vert f\left(z_n\right)-f\left(p\right)\Vert +\Vert f\left(p\right)-p\Vert \right)}^2\end{array}$

又因为 $f$ 是一个 $\kappa -$ 压缩，所以由上式可得：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n{\Vert z_n-p\Vert }^2\\ +{\beta }_n\left(2\Vert z_n-p\Vert \Vert f\left(p\right)-p\Vert +{\Vert f\left(p\right)-p\Vert }^2\right)\\ \le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n{\Vert z_n-p\Vert }^2+{\beta }_n{M}_2\end{array}$ (11)

因为 $\left\{z_n\right\}$ 有界，所以 $\left\{\Vert z_n-p\Vert \right\}$ 有界。

即令 $M_2:=2\Vert f\left(p\right)-p\Vert \underset{n\in \mathbb{N}}{\sup }\left\{\Vert z_n-p\Vert \right\}+{\Vert f\left(p\right)-p\Vert }^2$，得到 $M_2$ 是一个有界量，且 $M_2>0$。

把(4)代入(11)得到：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n{\Vert w_n-p\Vert }^2-{\theta }_n\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2\\ -{\theta }_n\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2+{\beta }_n{M}_2\end{array}$ (12)

通过(8)式我们得到：

$\begin{array}{c}{\Vert w_n-p\Vert }^2\le {\left(\Vert x_n-p\Vert +{\beta }_n{M}_1\right)}^2={\Vert x_n-p\Vert }^2+{\beta }_n\left(2M_1\Vert x_n-p\Vert +{\beta }_n{M}_1^2\right)\\ \le {\Vert x_n-p\Vert }^2+{\beta }_n{M}_3\end{array}$ (13)

其中 $M_3>0$。

把(13)式代入(12)式，得到：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le {\Vert x_n-p\Vert }^2-{\theta }_n\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2-{\theta }_n\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2+{\beta }_n\left(M_3+M_2\right)\\ \le {\Vert x_n-p\Vert }^2-{\theta }_n\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2-{\theta }_n\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2+{\beta }_n{M}_4\end{array}$

即得：

${\theta }_n\left(1-\tau L\right){\Vert y_n-w_n\Vert }^2+{\theta }_n\left(1-\tau L\right){\Vert z_n-y_n\Vert }^2\le {\Vert x_n-p\Vert }^2-{\Vert x_{n+1}-p\Vert }^2+{\beta }_n{M}_4$

其中 $M_4:=M_2+M_3$。 □

引理3.3 对于由算法生成的序列 $\left\{x_n\right\}$，以及 $p\in VI\left(C,A\right)$，有以下不等式成立：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-\left(1-\kappa \right){\beta }_n{\theta }_n\right){\Vert x_n-p\Vert }^2\\ +\left(1-\kappa \right){\beta }_n{\theta }_n\left[\frac{2}{1-\kappa }\langle f\left(p\right)-p,x_{n+1}-p\rangle +\frac{3M}{\left(1-\kappa \right){\theta }_n}\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert \right]\end{array}$

其中 $M:=\sup \left\{\Vert x_n-p\Vert ,\alpha \Vert x_n-x_{n-1}\Vert |n\in \mathbb{N}\right\}>0$。

证明：根据 $w_n$ 的定义我们有，

$\begin{array}{c}{\Vert w_n-p\Vert }^2={\Vert x_n+{\alpha }_n\left(x_n-x_{n-1}\right)-p\Vert }^2\\ ={\Vert x_n-p\Vert }^2+2{\alpha }_n\langle x_n-p,x_n-x_{n-1}\rangle +{\alpha }_n^2{\Vert x_n-x_{n-1}\Vert }^2\\ \le {\Vert x_n-p\Vert }^2+2{\alpha }_n\Vert x_n-p\Vert \Vert x_n-x_{n-1}\Vert +{\alpha }_n^2{\Vert x_n-x_{n-1}\Vert }^2\end{array}$ (14)

由 $x_{n+1}$ 的定义以及(2)式我们得到：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2=\Vert \left(1-{\theta }_n\right)\left(x_n-p\right)+{\theta }_n\left[\left(1-{\beta }_n\right)\left(\begin{array}{c}{z}_n-p\end{array}\right)+{\beta }_n\left(f\left(z_n\right)-f\left(p\right)\right)\right]{+{\theta }_n{\beta }_n\left(f\left(p\right)-p\right)\Vert }^2\\ \le \Vert \left(1-{\theta }_n\right)\left(x_n-p\right)+{\theta }_n\left[\left(1-{\beta }_n\right)\left(z_n-p\right)+{\beta }_n\left(f\left(z_n\right)-f\left(p\right)\right)\right]\Vert \\ +2{\theta }_n{\beta }_n\langle f\left(p\right)-p,x_{n+1}-p\rangle \end{array}$

接下来对上式左边的范数部分使用命题2.1，得到：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n\left(1-{\beta }_n\right){\Vert z_n-p\Vert }^2+{\theta }_n{\beta }_n{\Vert f\left(z_n\right)-f\left(p\right)\Vert }^2\\ +2{\theta }_n{\beta }_n\langle f\left(p\right)-p,x_{n+1}-p\rangle \end{array}$

因为 $f$ 是一个 $\kappa -$ 压缩， $\kappa \in \left[0,1\right)$，使用(5)式，

上式可得：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n\left(1-{\beta }_n\right){\Vert z_n-p\Vert }^2+{\theta }_n{\beta }_n\kappa {\Vert z_n-p\Vert }^2\\ +2{\theta }_n{\beta }_n\langle f\left(p\right)-p,x_{n+1}-p\rangle \\ \le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+{\theta }_n\left(1-\left(1-\kappa \right){\beta }_n\right){\Vert w_n-p\Vert }^2\\ +2{\theta }_n{\beta }_n\langle f\left(p\right)-p,x_{n+1}-p\rangle \end{array}$ (15)

把(14)式代入(15)式，可得：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-{\theta }_n\right){\Vert x_n-p\Vert }^2+\theta \left(1-\left(1-\kappa \right){\beta }_n\right){\Vert x_n-p\Vert }^2+2{\alpha }_n\Vert x_n-p\Vert \Vert x_n-x_{n-1}\Vert \\ +{\alpha }_n^2{\Vert x_n-x_{n-1}\Vert }^2+2{\theta }_n{\beta }_n\langle f\left(p\right)-p,x_{n+1}-p\rangle \\ =\left(1-\left(1-\kappa \right){\beta }_n{\theta }_n\right){\Vert x_n-p\Vert }^2+\left(1-\kappa \right){\beta }_n{\theta }_n\frac{2}{1-\kappa }\langle f\left(p\right)-p,x_{n+1}-p\rangle \\ +{\alpha }_n\Vert x_n-x_{n-1}\Vert \left(2\Vert x_n-p\Vert +{\alpha }_n\Vert x_n-x_{n-1}\Vert \right)\end{array}$

又因为 $0\le {\alpha }_n<\alpha$，所以由上式可得：

$\begin{array}{c}{\Vert x_{n+1}-p\Vert }^2\le \left(1-\left(1-\kappa \right){\beta }_n{\theta }_n\right){\Vert x_n-p\Vert }^2+\left(1-\kappa \right){\beta }_n{\theta }_n\frac{2}{1-\kappa }\langle f\left(p\right)-p,x_{n+1}-p\rangle \\ +{\alpha }_n\Vert x_n-x_{n-1}\Vert \left(2\Vert x_n-p\Vert +\alpha \Vert x_n-x_{n-1}\Vert \right)\\ \le \left(1-\left(1-\kappa \right){\beta }_n{\theta }_n\right){\Vert x_n-p\Vert }^2+\left(1-\kappa \right){\beta }_n{\theta }_n\frac{2}{1-\kappa }\langle f\left(p\right)-p,x_{n+1}-p\rangle +3M{\alpha }_n\Vert x_n-x_{n-1}\Vert \\ \le \left(1-\left(1-\kappa \right){\beta }_n{\theta }_n\right){\Vert x_n-p\Vert }^2\\ +\left(1-\kappa \right){\beta }_n{\theta }_n\left[\frac{2}{1-\kappa }\langle f\left(p\right)-p,x_{n+1}-p\rangle +\frac{3M}{\left(1-\kappa \right){\theta }_n}\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert \right]\end{array}$

其中： $M:=\sup \left\{\Vert x_n-p\Vert ,\alpha \Vert x_n-x_{n-1}\Vert |n\in \mathbb{N}\right\}>0$。 □

以下是定理3.1的证明：

证明：我们要证明 $\left\{{\Vert x_n-\hat{p}\Vert }^2\right\}$ 收敛到零，下面我们考虑序列 $\left\{{\Vert x_n-\hat{p}\Vert }^2\right\}$ 的两种情况：

(一)：存在 $N\in \mathbb{N}$，对任意的 $n\ge N$，使得 ${\Vert x_{n+1}-\hat{p}\Vert }^2\le {\Vert x_n-\hat{p}\Vert }^2$。

在引理3.1里证明了 $\left\{x_n\right\}$ 有界，故可以推出 $\left\{\Vert x_n-\hat{p}\Vert \right\}$ 是有界的，所以由 ${\Vert x_{n+1}-\hat{p}\Vert }^2\le {\Vert x_n-\hat{p}\Vert }^2$ 可以得到：

$\underset{n\to \infty }{\lim }\Vert x_n-\hat{p}\Vert$ 存在。

根据引理3.2，我们可以得到：

$\underset{n\to \infty }{\lim }\Vert y_n-w_n\Vert =0,\underset{n\to \infty }{\lim }\Vert z_n-y_n\Vert =0$ (16)

由于 $\left\{x_n\right\}$ 是有界的，就存在 $\left\{x_n\right\}$ 的一个子列 $\left\{x_{n_k}\right\}$ 令它收敛到 $z$，我们可以推出 $\left\{\langle f\left(\hat{p}\right)-p,x_n-\hat{p}\rangle \right\}$ 是有界的，那么存在其子列 $\left\{\langle f\left(\hat{p}\right)-\hat{p},x_{n_k}-\hat{p}\rangle \right\}$，使得：

$\underset{n\to \infty }{\lim \sup }\langle f\left(\hat{p}\right)-\hat{p},x_n-\hat{p}\rangle =\underset{k\to \infty }{\lim }\langle f\left(\hat{p}\right)-\hat{p},x_{n_k}-\hat{p}\rangle =\langle f\left(\hat{p}\right)-\hat{p},z-\hat{p}\rangle$ (17)

根据(16)和(文献 [19] 引理3.2)，我们可以得到 $z\in VI\left(C,A\right)$。

通过(17)、引理2.1(3)以及 $\hat{p}=P_{VI\left(C,A\right)}\circ f\left(\hat{p}\right)$，就有：

$\underset{n\to \infty }{\lim \sup }\langle f\left(\hat{p}\right)-\hat{p},x_n-\hat{p}\rangle =\langle f\left(\hat{p}\right)-\hat{p},z-\hat{p}\rangle \le 0$ (18)

现在我们证明：

$\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$ (19)

通过(16)可以得到：

$\Vert z_n-w_n\Vert =\Vert z_n-y_n+y_n-w_n\Vert \le \Vert z_n-y_n\Vert +\Vert y_n-w_n\Vert \to 0\left(n\to \infty \right)$ (20)

另一方面，我们有：

$\Vert x_n-w_n\Vert ={\alpha }_n\Vert x_n-x_{n-1}\Vert =\frac{{\alpha }_n}{{\beta }_n}\Vert x_n-x_{n-1}\Vert {\beta }_n\to 0\left(n\to \infty \right)$ (21)

$\Vert x_n-z_n\Vert \le \Vert x_n-w_n\Vert +\Vert w_n-y_n\Vert +\Vert y_n-z_n\Vert \to 0\left(n\to \infty \right)$ (22)

所以由 $x_{n+1}$ 的定义以及(22)式可以得到：

$\begin{array}{c}\Vert x_{n+1}-z_n\Vert =\Vert \left(1-{\theta }_n\right)\left(x_n-z_n\right)+{\theta }_n{\beta }_n\left(f\left(z_n\right)-z_n\right)\Vert \\ \le \left(1-{\theta }_n\right)\Vert x_n-z_n\Vert +{\theta }_n{\beta }_n\Vert f\left(z_n\right)-z_n\Vert \to 0\left(n\to \infty \right)\end{array}$ (23)

根据(20)、(21)和(23)式，可以推出：

$\Vert x_{n+1}-x_n\Vert \le \Vert x_{n+1}-z_n\Vert +\Vert z_n-w_n\Vert +\Vert w_n-x_n\Vert \to 0\left(n\to \infty \right)$

所以这就证明了 $\underset{n\to \infty }{\lim }\Vert x_{n+1}-x_n\Vert =0$。

结合(18)和(19)式，我们有：

$\underset{n\to \infty }{\lim \sup }\langle f\left(\hat{p}\right)-\hat{p},x_{n+1}-\hat{p}\rangle =\underset{n\to \infty }{\lim \sup }\langle f\left(\hat{p}\right)-\hat{p},x_n-\hat{p}\rangle =\langle f\left(\hat{p}\right)-\hat{p},z-\hat{p}\rangle \le 0$

因此，根据(文献 [18] 引理2.1)和引理3.3，我们就可以得到 $\underset{n\to \infty }{\lim }\Vert x_n-\hat{p}\Vert =0$。

(二)：存在 $\left\{{\Vert x_n-\hat{p}\Vert }^2\right\}$ 的子序列 $\left\{{\Vert x_{n_j}-\hat{p}\Vert }^2\right\}$，使得对任意的 $j\in \mathbb{N}$ 有

${\Vert x_{n_j}-\hat{p}\Vert }^2<{\Vert x_{n_j+1}-\hat{p}\Vert }^2$。

在这种情况下，根据(文献 [20] 引理2.3)，存在一个非减序列 $\left\{m_k\right\}\subset \mathbb{N}$，使得 $\underset{k\to \infty }{\lim }{m}_k=\infty$，并有以下不等式成立：

对任意的 $k\in \mathbb{N}$

${\Vert x_{m_k}-\hat{p}\Vert }^2\le {\Vert x_{m_k+1}-\hat{p}\Vert }^2\text{,}{\Vert x_k-\hat{p}\Vert }^2\le {\Vert x_{m_k+1}-\hat{p}\Vert }^2$ (24)

根据引理3.2，我们有：

${\theta }_{m_k}\left(1-\tau L\right){\Vert y_{m_k}-w_{m_k}\Vert }^2+{\theta }_{m_k}\left(1-\tau L\right){\Vert z_{m_k}-y_{m_k}\Vert }^2\le {\Vert x_{m_k}-\hat{p}\Vert }^2-{\Vert x_{m_k+1}-\hat{p}\Vert }^2+{\beta }_{m_k}{M}_4\le {\beta }_{m_k}{M}_4$

因此，我们得到

$\underset{k\to \infty }{\lim }\Vert y_{m_k}-w_{m_k}\Vert =0,\underset{k\to \infty }{\lim }\Vert z_{m_k}-y_{m_k}\Vert =0$

与(一)的证明类似，我们可以得到：

$\Vert x_{m_k+1}-x_{m_k}\Vert \to 0\left(k\to 0\right)和\underset{k\to \infty }{\lim \sup }\langle f\left(\hat{p}\right)-\hat{p},x_{m_k+1}-\hat{p}\rangle \le 0$

根据引理3.3，有：

$\begin{array}{c}{\Vert x_{m_k+1}-\hat{p}\Vert }^2\le \left(1-\left(1-\kappa \right){\beta }_{m_k}{\theta }_{m_k}\right){\Vert x_{m_k}-\hat{p}\Vert }^2\\ +\left(1-\kappa \right){\beta }_{m_k}{\theta }_{m_k}\left[\frac{2}{1-\kappa }\langle f\left(\hat{p}\right)-\hat{p},x_{m_k+1}-\hat{p}\rangle +\frac{3M}{\left(1-\kappa \right){\theta }_{m_k}}\frac{{\alpha }_{m_k}}{{\beta }_{m_k}}\Vert x_{m_k}-x_{m_k-1}\Vert \right]\end{array}$

通过(24)和上式，有：

$\begin{array}{c}{\Vert x_{m_k+1}-\hat{p}\Vert }^2\le \left(1-\left(1-\kappa \right){\beta }_{m_k}{\theta }_{m_k}\right){\Vert x_{m_k+1}-\hat{p}\Vert }^2\\ +\left(1-\kappa \right){\beta }_{m_k}{\theta }_{m_k}\left[\frac{2}{1-\kappa }\langle f\left(\hat{p}\right)-\hat{p},x_{m_k+1}-\hat{p}\rangle +\frac{3M}{\left(1-\kappa \right){\theta }_{m_k}}\frac{{\alpha }_{m_k}}{{\beta }_{m_k}}\Vert x_{m_k}-x_{m_k-1}\Vert \right]\end{array}$

所以，我们得到：

${\Vert x_{m_k+1}-\hat{p}\Vert }^2\le \frac{2}{1-\kappa }\langle f\left(\hat{p}\right)-\hat{p},x_{m_k+1}-\hat{p}\rangle +\frac{3M}{\left(1-\kappa \right){\theta }_{m_k}}\frac{{\alpha }_{m_k}}{{\beta }_{m_k}}\Vert x_{m_k}-x_{m_k-1}\Vert$

因此，我们可以推出：

$\underset{k\to \infty }{\lim \sup }\Vert x_{m_k+1}-\hat{p}\Vert ⩽0$ (25)

结合(24)和(25)，我们有：

$\underset{k\to \infty }{\lim \sup }\Vert x_k-\hat{p}\Vert \le 0$，所以就有 $x_k\to \hat{p}\left(k\to \infty \right)$ □

4. 结语

变分不等式问题是优化领域里的一个被学者们广泛研究的问题，而用以求解变分不等式问题的次梯度外梯度算法更是专家学者们的重点关注对象，但大部分文献里的次梯度外梯度算法都只证明了算法的弱收敛性，本文针对Duong和Dang提出的惯性次梯度外梯度算法，结合粘度逼近法，提出了一种具有强收敛性的修正惯性次梯度外梯度算法。

NOTES

^*通讯作者。