一类特殊的保形映射

A Special Class of Conformal Mappings

摘要: 保形映射理论是复变函数的重要内容之一，它在许多科学技术领域中有广泛的应用。本文主要对一类特殊的保形映射进行研究，通过角形区域和圆弧区域的变化规律得到此类保形映射的通式。

Abstract: The theory of conformal mapping is one of the important contents of complex function and has a few applications to many scientific and technical fields. In this paper, we show a special class of conformal mappings. The main focus is to obtain the general formula of those conformal mappings by the rules for changing the angular and arc region.

1. 引言

解析函数是复变函数中一类具有解析性质的函数，复变函数论主要就是研究复数域上的解析函数。2000年来，其核心定理“柯西–黎曼”方程组一直被数学界公认是不能分开的。而解析函数所确定的映射是保形映射，它是复变函数论中最重要的概念之一(详见参考文献 [1] )。保形映射使几乎不可能的事物变得简单。随着科技的进步，保形映射与物理学有着紧密联系，而且对物理学中的许多领域有重要的应用，如：应用保形映射成功解决了流体力学与空气动力学、磁场和电场及其他方面的许多问题。

目前，国内外对保形映射的研究有很多，如：Schwarz-Christoffel保形映射的解析，它探讨了正多边形到圆盘空间上的保形映射等复杂内容(详见参考文献 [2] [3] )，是保形映射更加广泛的应用及其与其他数学定理或概念之间的联系。而本文主要对一类特殊的保形映射进行研究，主要内容有：象限平面区域到一个半圆区域的保形映射、一个特定角形区域的保形映射和一般角形区域的保形映射等。

本文主要分为三个部分。

第一部分内容主要针对象限平面映射为半圆域而进行探究，以第一、二象限(所形成 $\frac{\pi }{2}$ 角平面)为例，

得到以下规律：

① 当z平面区域(第一象限平面)旋转一定角度 $\theta$， $\omega$ 平面固定为上半圆域时，映射为

$\omega =R\frac{{\text{e}}^{-i\theta }z-1}{{\text{e}}^{-i\theta }z+1}$

② 当 $\omega$ 平面的半圆域旋转一定角度 $\beta$，z平面固定为第一象限时，映射为

$\omega ={\text{e}}^{i\beta }R\frac{z-1}{z+1}$

③ 当z平面区域(第一象限平面)旋转一定角度 $\theta$， $\omega$ 平面的上半圆域旋转一定角度 $\beta$ 时，映射为

$\omega ={\text{e}}^{i\beta }R\frac{{\text{e}}^{-i\theta }z-1}{{\text{e}}^{-i\theta }z+1}$

第二部分内容主要针对特定角形区域的映射进而推广至一般角形区域的映射而进行探究，得到以下规律：

④ 当z平面区域以原点为顶点，所形成 $\alpha$ 角平面， $\omega$ 平面固定为上半圆域时，映射为

$\omega =R\frac{z^{\frac{\pi }{2\alpha }}-1}{z^{\frac{\pi }{2\alpha }}+1}$

⑤ 当 $\omega$ 平面区域以原点为顶点，所形成 $\gamma$ 角圆弧域，z平面固定为第一象限时，映射为

$\omega =R{\left(\frac{z-1}{z+1}\right)}^{\frac{\gamma }{\pi }}$

⑥ 当z平面区域以原点为顶点，所形成 $\alpha$ 角平面且旋转一定角度 $\theta$ ； $\omega$ 平面区域以原点为顶点，所形成 $\gamma$ 角圆弧域且旋转一定角度 $\beta$ 时，映射为

$\omega ={\text{e}}^{i\beta }R{\left[\frac{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}-1}{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}+1}\right]}^{\frac{\gamma }{\pi }}$

第三部分内容基于z平面区域以原点为顶点，所形成 $\alpha$ 角平面且旋转一定角度 $\theta$ ； $\omega$ 平面区域以原点为顶点，所形成 $\gamma$ 角圆弧域且旋转一定角度 $\beta$ 时的映射(即第二部分的⑥)，主要针对不以原点为顶点的角形区域的保形映射而进行探究，得到以下规律：

⑦ 当z平面区域顶点变为 $a+bi$ 时，映射变为

$\omega ={\text{e}}^{i\beta }R{\left\{\frac{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}-1}{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}+1}\right\}}^{\frac{\gamma }{\pi }}$

⑧ 当 $\omega$ 平面区域顶点变为 $m+ni$ 时，映射为

$\omega ={\text{e}}^{i\beta }R{\left[\frac{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}-1}{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}+1}\right]}^{\frac{\gamma }{\pi }}+\left(m+ni\right)$

⑨ 当z平面区域顶点变为 $a+bi$， $\omega$ 平面区域顶点变为 $m+ni$ 时，映射为

$\omega ={\text{e}}^{i\beta }R{\left\{\frac{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}-1}{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}+1}\right\}}^{\frac{\gamma }{\pi }}+\left(m+ni\right)$

最后得到角形区域到圆弧域映射的一般通式：

$\omega ={\text{e}}^{i\beta }R{\left\{\frac{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}-1}{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}+1}\right\}}^{\frac{\gamma }{\pi }}+\left(m+ni\right)$

通过此探究，希望可以为之后保形映射的学术研究提供更多的资料和数据。

2. 象限平面区域到半圆域的保形映射

我们首先找到象限平面到半圆域的映射方法，进而求出不同象限到半圆域的保形映射，最终得到相应的映射规律，主要分为以下两部分。

2.1. 象限平面到半圆域保形映射的方法

对于象限平面到半圆域的映射，我们以第一象限保形映射为上半圆域为例(如图1所示)，之后探究均基于该例进行。显然，我们很难通过保交比来直接确定相应映射，故可采用求逆运算的方式求解，即先找到上半圆域到第一象限的保形映射，进而求逆运算来确定第一象限到上半圆域的映射。

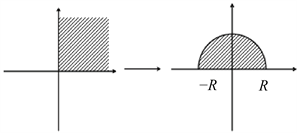
Figure 1. Mapping from the first quadrant to the upper semicircular domain

图1. 第一象限到上半圆域的映射

如图2所示，若将半圆域映射为角形区域，则应当将直径的两端点分别映射为原点和无穷远点。故作映射将

$-R\to 0,R\to \infty$

设

$\omega =k\frac{z+R}{z-R}$

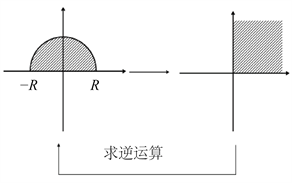
Figure 2. Mapping from the upper semicircle to the first quadrant

图2. 上半圆域到第一象限的映射

由于半圆圆周与直径在 $-R$ 处夹角为 $\frac{\pi }{2}$，因此只需要将原点映射到 $\omega$ 平面实轴的正向即可。将 $z=0$

代入

$\omega =k\frac{z+R}{z-R}$

得：

$\omega =-k>0$

即 $k<0$。

此时，k取不同值时，映射也有所不同，如表1所示。

Table 1. The effect of k value on the mapping

表1. k值对映射的影响

为了研究方便，下列研究均取 $k=-1$，则取逆运算后，得：

$z=R\frac{\omega -1}{\omega +1}$

则图1的映射为

$\omega =R\frac{z-1}{z+1}$ (1)

因此，对于象限平面到半圆域的保形映射，本文主要采用的是求逆运算的方式。

2.2. 象限平面到半圆域保形映射的规律

通过对第一象限、第二象限保形映射为不同半圆域进行探究，主要通过旋转变换和求逆运算来获得相应保形映射，最后通过观察区域旋转对公式(1)的影响(表2、表3)。

Table 2. Conformal mapping of the first quadrant region

表2. 第一象限区域的保形映射

Table 3. Conformal mapping of the second quadrant region

表3. 第二象限区域的保形映射

注：下图3是表3②的证明。

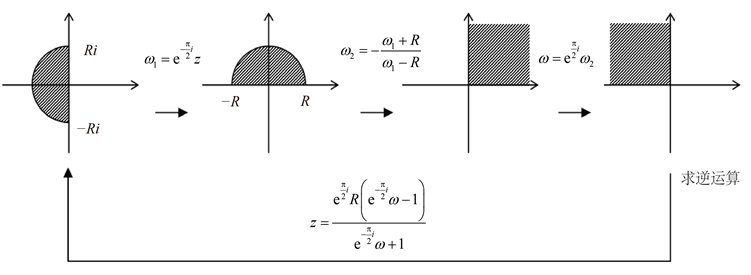
Figure 3. Solving the second quadrant to left semicircle domain mapping

图3. 第二象限到左半圆域的映射求解

其他证明类似。

根据观察，我们得到当 $\omega$ 平面的半圆域旋转一定角度 $\beta$ 时，仅仅是对公式(1)整体产生影响，此时映射为：

$\omega ={\text{e}}^{i\beta }R\frac{z-1}{z+1}$

当z平面的象限区域旋转一定角度 $\theta$ 时，仅仅是对公式(1)中的z产生影响，在z的前面乘于 ${\text{e}}^{-i\theta }$，此时映射为：

$\omega =R\frac{{\text{e}}^{-i\theta }z-1}{{\text{e}}^{-i\theta }z+1}$

我们可以在第三、四象限中运用此规律，可以发现得到的保形映射与最初求逆运算得到的保形映射一致，则证明该规律是正确的。

3. 特定角度平面的保形映射

第一部分探究了象限平面到半圆域的保形映射，主要探究了区域旋转对公式(1)的影响，以下是以特

定角度 $\frac{\pi }{4}$ 、 $\frac{\pi }{3}$ 、 $\frac{\pi }{6}$ 为例，来探究特定角度区域的保形映射并观察映射的规律，主要分为以下三个部分。

3.1. z平面区域角度的变化

首先，我们先固定平面为上半圆域(默认半径为R)，仅仅使z平面区域的角度发生变化，来观察z平面区域的角度变化对公式(1)的影响，如表4所示。

其他证明类似。

根据观察，我们发现：当z平面区域以原点为顶点，所形成 $\alpha$ 角平面时，仅仅对公式(1)中z的指数有影响，此时映射为：

$\omega =R\frac{z^{\frac{\pi }{2\alpha }}-1}{z^{\frac{\pi }{2\alpha }}+1}$

Table 4. The effect of angle changes in the z plane region on mapping

表4. z平面区域角度的变化对映射的影响

注：下图4是表4①的证明。

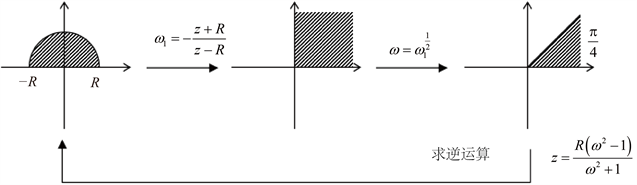
Figure 4. Solving the mapping from $\frac{\pi }{4}$ plane region to upper semicircle region

图4. $\frac{\pi }{4}$ 平面区域到上半圆域的映射求解

3.2. $\omega$ 平面区域角度的变化

我们固定z平面区域(第一象限)，仅仅使 $\omega$ 平面区域的角度发生变化，来观察 $\omega$ 平面区域的角度变化对公式(1)的影响，如表5所示。

Table 5. The effect of angle changes in the ω plane region on mapping

表5. $\omega$ 平面区域角度的变化对映射的影响

注：下图5是表5②的证明。

其他证明类似。

根据观察，我们发现：当 $\omega$ 平面区域以原点为顶点，所形成 $\gamma$ 角圆弧域，此时映射为：

$\omega =R{\left(\frac{z-1}{z+1}\right)}^{\frac{\gamma }{\pi }}$

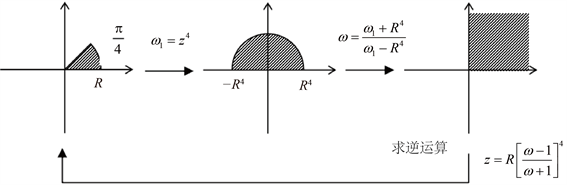
Figure 5. Solving the mapping from the first quadrant to the $\frac{\pi }{4}$ plane region

图5. 第一象限到 $\frac{\pi }{4}$ 平面区域的映射求解

3.3. 特定角度区域旋转之后的保形映射

接下来，我们来判断对于特定角形区域的保形映射是否依旧满足区域旋转的规律(即第一部分所得到

的规律)。以 $\frac{\pi }{6}$ 角形区域映射为 $\frac{\pi }{6}$ 圆弧域为例，假设z平面区域旋转了 $\theta$ 角， $\omega$ 平面旋转了 $\beta$ 角，如图6所示。

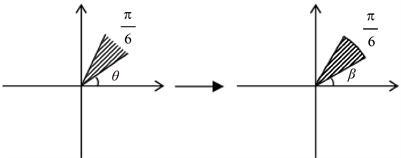
Figure 6. Mapping from $\frac{\pi }{6}$ angle region to $\frac{\pi }{6}$ circular region

图6. $\frac{\pi }{6}$ 角形区域到 $\frac{\pi }{6}$ 圆弧域的映射

证明如下图7所示：

我们发现，所求得的映射依旧满足区域旋转的规律。则此时假设z平面区域为 $\alpha$ 角平面，旋转了 $\theta$ 角； $\omega$ 平面区域为 $\gamma$ 角圆弧域，旋转了 $\beta$ 角(如图8所示)，此时的映射为：

$\omega ={\text{e}}^{i\beta }R{\left[\frac{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}-1}{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}+1}\right]}^{\frac{\gamma }{\pi }}$ (2)

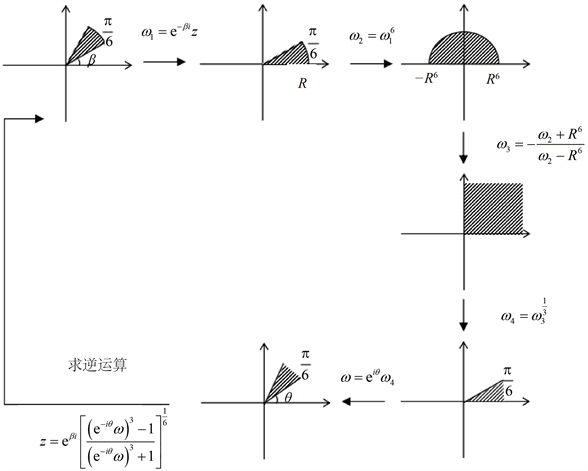
Figure 7. Solving the mapping from $\frac{\pi }{6}$ angle region to $\frac{\pi }{6}$ circular region

图7. $\frac{\pi }{6}$ 角形区域到 $\frac{\pi }{6}$ 圆弧域的映射求解

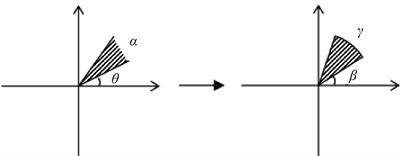
Figure 8. Mapping from $\alpha$ angle region to $\gamma$ circular region

图8. $\alpha$ 角形区域到 $\gamma$ 角圆弧域的映射

4. 不以原点为顶点区域的保形映射

上述内容均是以原点为顶点的区域，以下探究我们首先以两条坐标轴上的点为顶点，然后推广至复平面中任意一点为顶点，观察保形映射的变化。整体研究基于z平面区域以原点为顶点，所形成 $\alpha$ 角平面且旋转一定角度 $\theta$ ； $\omega$ 平面区域以原点为顶点，所形成 $\gamma$ 角圆弧域且旋转一定角度 $\beta$ 时的映射(即公式(2))。主要包括以下三部分。

4.1. z平面区域顶点变化

先固定 $\omega$ 平面区域(以原点为顶点， $\gamma$ 角圆弧域，旋转了 $\beta$ 角)，仅仅使z平面区域的顶点发生变化，找到相应的保形映射，如表6所示。

Table 6. The effect of vertex changes in the z plane region on the mapping

表6. z平面区域顶点的变化对映射的影响

注：下图9是表6③的证明。

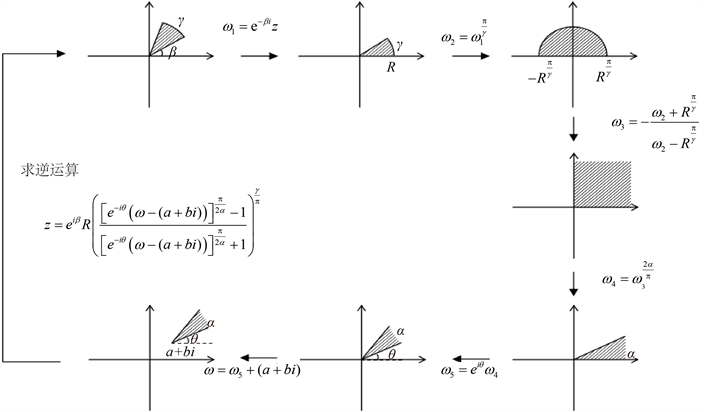
Figure 9. Solving the mapping of the z plane region with vertex $a+bi$

图9. 顶点为 $a+bi$ 的z平面区域的映射求解

其他证明类似。

我们发现，z平面区域顶点的变化仅仅使z发生了变化。若顶点变为 $a+bi$，此时映射为：

$\omega ={\text{e}}^{i\beta }R{\left\{\frac{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}-1}{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}+1}\right\}}^{\frac{\gamma }{\pi }}$

4.2. $\omega$ 平面区域顶点的变化

先固定z平面区域(以原点为顶点， $\alpha$ 角平面域，旋转了 $\theta$ 角)，仅仅使 $\omega$ 平面区域的顶点发生变化，找到相应的保形映射，如表7所示。

Table 7. The effect of vertex changes in the ω plane region on the mapping

表7. $\omega$ 平面区域顶点的变化对映射的影响

注：下图10是表7③的证明。

其他证明类似。

根据表格，我们发现， $\omega$ 平面区域顶点的变化仅仅使z发生了变化。若顶点变为 $m+ni$，此时映射为：

$\omega ={\text{e}}^{i\beta }R{\left[\frac{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}-1}{{\left({\text{e}}^{-i\theta }z\right)}^{\frac{\pi }{2\alpha }}+1}\right]}^{\frac{\gamma }{\pi }}+\left(m+ni\right)$

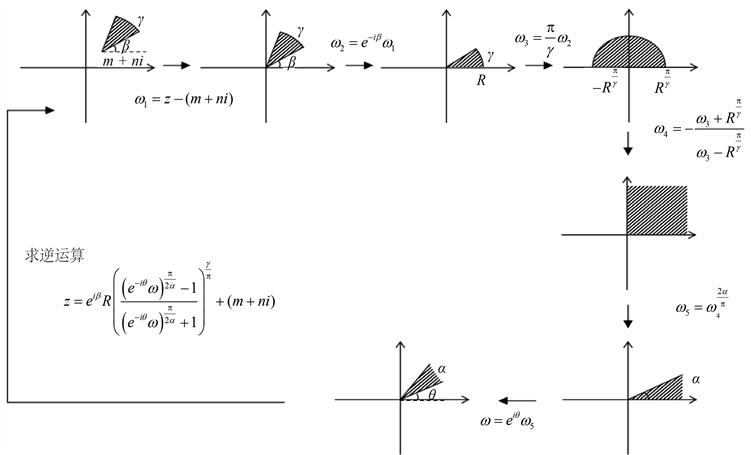
Figure 10. Solving the mapping of $\gamma$ -arc domain with vertex $m+ni$

图10. 顶点为 $m+ni$ 的 $\gamma$ 圆弧域的映射求解

4.3. z、 $\omega$ 平面区域顶点均发生变化

假设z平面区域为 $\alpha$ 角平面，以 $a+bi$ 为顶点，旋转了 $\theta$ 角； $\omega$ 平面区域为 $\gamma$ 角圆弧域，以 $m+ni$ 为顶点，旋转了 $\beta$ 角(如图11)。则根据上述规律，得到此时的映射为：

$\omega ={\text{e}}^{i\beta }R{\left\{\frac{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}-1}{{\left[{\text{e}}^{-i\theta }\left(z-\left(a+bi\right)\right)\right]}^{\frac{\pi }{2\alpha }}+1}\right\}}^{\frac{\gamma }{\pi }}+\left(m+ni\right)$ (3)

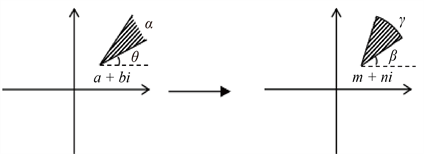
Figure 11. Mapping of general angular region to circular region

图11. 一般角形区域到圆弧域的映射

此映射与求逆运算所得到的结果一致，如图12所示。该公式(3)即为角形区域到圆弧域保形映射的一般通式。

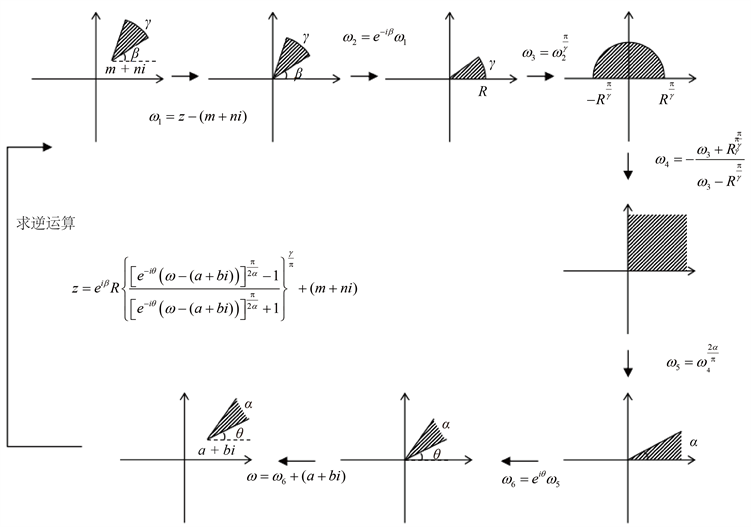
Figure 12. Solving the mapping of general angular region to circular region

图12. 一般角形区域到圆弧域的映射求解

致谢

本篇论文的顺利完成离不开全员的共同努力，离不开《大学生创新创业训练计划项目》给我们的这个平台。 通过这次项目，我们不仅有机会将自己的知识展示出来，而且在撰写论文的过程中也收获颇丰。 因此，在这里我们诚挚地感谢《大学生创新创业训练计划项目》，也非常感谢团队之间的团结协作。

基金项目

辽宁师范大学2021年度大学生创新创业训练计划项目资助。

NOTES

^*通讯作者。