次三正则图最小极大匹配上界的改进

Improvement of Upper Bound of Minimum Maximal Matching in Subcubic Graphs

摘要: 图G的边控制数是图中最大匹配的最小大小。众所周知，这个参数计算起来很困难。Julien Baste根据正则图和非正则图的阶数及最大度给出了最优可能上界。研究了边支配数的上界和相关算法，他给出了次三正则二部不含T*图的最小极大匹配的上界。其中T^*是由爪形图的两条边恰好细分一次而形成的树。本文在此基础上，改进了其中次三正则图边控制数的上界，并作出一些推论。

Abstract: The edge control number Υ(G) of graph G is the minimum size of a maximal match in the graph. This parameter is notoriously difficult to calculate. Julien Baste gives the optimal possible upper bound according to the order and maximum degree of regular graph and non-regular graph. In this paper, we study the upper bound and correlation algorithm of edge dominating numbers. He gives the upper bound of minimum maximal matching of subcubic bipartite T*-free graph, where T* is the tree formed by subdividing the two edges of the claw graph exactly once. On this basis, we improve the upper bound of the edge control numbers of the subcubic graphs, and make some inferences.

1. 引言

我们考虑的是有限的、简单的且无向的图，并使用标准术语。设G是一个图，M是图G的边集合， $V\left(M\right)$ 表示图G中与M中一条边相关联的顶点集合。若图G的最大次数不超过三次，则称图G是次三正则图，若图G的所有点的度数均为3，则称其为三正则图。如果M中的边是成对不相交的，则集合M是图G中的一个匹配。图G中的匹配M是极大的即集合 $V\left(G\right)\backslash V\left(M\right)$ 是独立的。设图G的边支配数 $\gamma \left(G\right)$ 是图G中极大匹配的最小大小。在图G中极大匹配的大小为 $\gamma \left(G\right)$ 即为最小的极大匹配。

关于边支配数和最小的极大匹配的研究已经进行了很长的时间，Yannakakis和Gavril [1] 证明，即使对于最大次数为3的平面图或者二部图，寻找最小极大匹配也是NP-hard。关于如何更便捷的得到一些图的最小极大匹配，一些学者研究了启发式算法和近似算法 [2] [3] [4]。

Julien Baste [5] 研究了边支配数的上界和相关算法，他给出了次三正则二部不含 $T^{\ast }$ 图的最小极大匹配的上界。其中 $T^{\ast }$ 是由爪形图 $K_{1,3}$ 的两条边恰好细分一次而形成的 [6]。回想一下，一个图是不含 $T^{\ast }$ 的即它不包含 $T^{\ast }$ 作为导出子图。

2. 主要结论及其证明

定理1 若G是n个点的连通三正则二部图且不含 $T^{\ast }$，则 $\gamma \left(G\right)\le \frac{2n}{5}+\frac{3}{5}$。

定理2 若G是点数为n，边数为m的次三正则二部图且不含 $T^{\ast }$，使G无连通分量为三正则图，则：

$\{\begin{array}{l}\gamma \left(G\right)=6,图G为{\rm I}类图\\ \gamma \left(G\right)\le \frac{7n}{10}-\frac{m}{5},其他\end{array}$

其中I类图包含图1(a)和图1(b)，如图1所示。

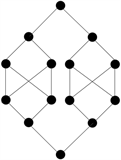(a) (b)

Figure 1. Two cases of graphs of class I. (a) $n=15$, $m=21$, $\gamma \left(G\right)=6$ ; (b) $n=14$, $m=20$, $\gamma \left(G\right)=6$

图1. I类图的两种情况。(a) $n=15$， $m=21$， $\gamma \left(G\right)=6$ ；(b) $n=14$， $m=20$， $\gamma \left(G\right)=6$

证明 假设图G是定理2的一个反例，它使 $\left|V\left(G\right)\right|$ 最小。我们通过一系列引理来描述图G的性质，最终导致矛盾。在各种情况下，我们将从图G中删除一些顶点并添加一些边，然后对生成的子图进行归纳应用。我们将用 $G^{\prime },G^{″},\cdots$ 表示图G的子图， $n^{\prime },n^{″},\cdots$ 和 $m^{\prime },m^{″},\cdots$ 分别表示对应子图的点数和边数。M表示图G的极大匹配， $M^{\prime },M^{″},\cdots$ 表示对应子图的极大匹配。因为图G中不含 $T^{\ast }$，故图G的子图必然不含I类图。

引理1 图G的最小度为2。

证明 为得到矛盾，不妨假设 $d\left(u\right)=1$。设点v是点u的唯一邻居，点w是点v的不同于点u的邻居。若令 $G^{\prime }=G-\left\{u,v,w\right\}$，则 $n-n^{\prime }=3$， $m-m^{\prime }\le 5$， $M:=M^{\prime }+\left\{vw\right\}$。于是在中图G有：

$\gamma \left(G\right)\le \frac{7n^{\prime }}{10}-\frac{m^{\prime }}{5}+1\le \frac{7}{10}\left(n-3\right)-\frac{1}{5}\left(m-5\right)+1<\frac{7n}{10}-\frac{m}{5}$

矛盾，证明结束。

引理2 图G中的4圈不含2度点。

证明假设 $u{v}_1{v}_{2}wu$ 是图G中的一个4圈，其中 $d\left(u\right)=2$。显然 $C_4$ 不是反例，故不妨假设 $d\left(v_1\right)=3$。设点 $w_1$ 是点 $v_1$ 的邻居，若令 $G^{\prime }=G-\left\{u,v_1,v_2,w,w_1\right\}$，则 $n-n^{\prime }=5$， $m-m^{\prime }\le 9$， $M:=M^{\prime }+\left\{v_1{w}_1,v_{2}w\right\}$。若 $m-m^{\prime }\le 7$，我们会得到同引理1相同的矛盾。故 $8\le m-m^{\prime }\le 9$。先考虑 $m-m^{\prime }=8$ 的情况，不妨假设 $d\left(w\right)=2$， $d\left(w_1\right)=d\left(v_2\right)=3$。设点 $z_1,{z^{\prime }}_1$ 是点 $w_1$ 的邻居，点 $w_2$ 是点 $v_2$ 的邻居。若令 $G^{″}=G-\left\{u,v_1,v_2,w,w_1,w_2\right\}$，则 $n-n^{″}=6$， $m-m^{″}\le 10$， $M:=M^{″}+\left\{v_1{w}_1,v_2{w}_2\right\}$。于是在图G中有：

$\gamma \left(G\right)\le \frac{7n^{″}}{10}-\frac{m^{″}}{5}+2\le \frac{7}{10}\left(n-6\right)-\frac{1}{5}\left(m-10\right)+2<\frac{7n}{10}-\frac{m}{5}$

矛盾，证明结束。

故 $d\left(w\right)=3$。若 $d\left(v_2\right)=2$，则点 $w_1$ 有两个邻居为点 $z_1,{z^{\prime }}_1$，因为图G中不含 $T^{\ast }$，故点w与点 $w_1$ 有公共的邻居为点 ${z^{\prime }}_1$，又因为图G为二部图，则点 $z_1$ 有一个邻居为点 $z_2$，图G不含 $T^{\ast }$，则点 ${z^{\prime }}_1$ 与点 $z_2$ 相互接连。若令 $G^{‴}=G-\left\{u,v_1,v_2,w,w_1,z_1,{z^{\prime }}_1,z_2\right\}$，则 $n-n^{\prime }=8$， $m-m^{\prime }\le 12$， $M:=M^{‴}+\left\{u{v}_1,z_1{z}_2,{z^{\prime }}_{1}w\right\}$ 于是在图G中有：

$\gamma \left(G\right)\le \frac{7n^{‴}}{10}-\frac{m^{‴}}{5}+2\le \frac{7}{10}\left(n-8\right)-\frac{1}{5}\left(m-12\right)+3<\frac{7n}{10}-\frac{m}{5}$

矛盾。

故 $d\left(v_2\right)=d\left(w\right)=3$。则点 $v_2$ 的邻居是点 $z_2$，点w的邻居是点 ${z^{\prime }}_1$。因为图G中不含 $T^{\ast }$，故点 ${z^{\prime }}_1$ 与点 $z_2,w_1$ 相互接连且 $d\left(w\right)=2$ (否则有 $T^{\ast }$ )，此时的图G是 $n=7$ 的图，如图2所示，可知图G并非反例。

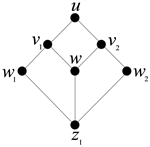
Figure 2. The graph G in the case that vertex ${z^{\prime }}_1$ is adjacent to vertext $z_2,w_1$ and $d\left(w\right)=2$. Note that $\left\{u{v}_1,w{z}_2\right\}$ is a maximal matching of G, which implies $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

图2. 图G在点 ${z^{\prime }}_1$ 与点 $z_2,w_1$ 相互接连且 $d\left(w\right)=2$ 的情况下。 $\left\{u{v}_1,w{z}_1\right\}$ 是其一个极大匹配，可知 $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

因此 $m-m^{\prime }=9$，则 $d\left(w\right)=d\left(w_1\right)=d\left(v_2\right)=3$。设点 $z_1,{z^{\prime }}_1$ 是点 $w_1$ 的邻居，点z是点w的邻居。因为图G是二部图，则 $w\ne z,w_2\ne z$，由对称性知 $d\left(w_2\right)=3$。若点z不与点 $w_1$ 相互接连，则 $T^{*}:=G\left[\left\{u,v_1,w_1,z,w,z_1\right\}\right]$，矛盾。故由对称性知，点z与点 $w_1,w_2$ 相互接连。点 $w_1$ 的邻居为点 $z_1$，若点 $z_1$ 与点 $w_2$ 相互接连，因为图G不含 $T^{\ast }$，则 $d\left(z_1\right)=2$， $n=8$，如图3所示，可知图G非反例。

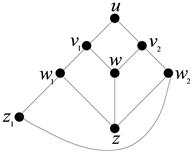
Figure 3. The graphs G in the case that $d\left(z_1\right)=2$, $n=8$. Note that $\left\{u{v}_1,wz,w_2{z}_1\right\}$ is a maximal matching of G, which implies $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

图3. 图G在 $d\left(z_1\right)=2$， $n=8$ 的情况下。 $\left\{u{v}_1,wz,w_2{z}_1\right\}$ 是其一个极大匹配，可知 $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

故点 $z_1$ 不与点 $w_2$ 相互接连，但在图G中有 $T^{*}:=G\left[\left\{u,v_1,w_1,z,z_1,w_2\right\}\right]$，矛盾，证明结束。

证明定理2

证明 令 $d\left(u\right)=2$，设点u的邻居为点 $v_1,v_2$，点 $w_i$ 是点 $v_i$ 的邻居 $\left(i\in \left[1,2\right]\right)$。根据引理2可知，点 $v_1,v_2$ 只有一个公共的邻居为点u。若令 $G^{\prime }=G-\left\{u,v_1,v_2,w_1,w_2\right\}$，则 $m-m^{\prime }\le 10$。因为在图 $G^{\prime }$ 的极大匹配中添加边集合 $\left\{v_1{w}_1,v_2{w}_2\right\}$ 会成为图G的极大匹配，所以如果 $m-m^{\prime }\le 7$，会得到同引理1中相同的矛盾，故 $m-m^{\prime }\ge 8$。

首先假设 $d\left(v_1\right)=d\left(v_2\right)=2$。则点 $w_i$ 有两个邻居为点 $z_i,{z^{\prime }}_i$ $\left(i\in \left[1,2\right]\right)$。因为图G是二部图，故点 $z_1,{z^{\prime }}_1$ 不能与点 $z_2,{z^{\prime }}_2$ 相互接连。由引理1可设点 $z_1$ 的邻居是点 $z_3$，因为图G不含 $T^{\ast }$，故点 ${z^{\prime }}_1$ 与点 $z_3$ 相互接连。由引理2可知，点 $z_1$ 有一个邻居为点 ${z^{\prime }}_3$。因为图G不含 $T^{\ast }$，则点 ${z^{\prime }}_1$ 与点 $z_3$ 相互接连。又根据引理2可知，点 $z_3$ 有一个邻居为点x，因为图G中不包含 $T^{\ast }$，则点 ${z^{\prime }}_3$ 与点x相互接连。同理，由定理2和图G不包含 $T^{\ast }$ 可知，点 $z_2$ 有两个邻居为点 $z_4,{z^{\prime }}_4$，点 ${z^{\prime }}_2$ 也与点 ${z^{\prime }}_4$ 相互接连，且点 $z_4,{z^{\prime }}_4$ 有公共的邻居为点 $x^{\prime }$。若令 $G^{\prime }=G-\left\{u,v_1,v_2,w_1,w_2,z_1,{z^{\prime }}_1,z_2,{z^{\prime }}_2,z_3,{z^{\prime }}_3,z_4,{z^{\prime }}_4,x,x^{\prime }\right\}$，则 $n-n^{\prime }=15$， $m-m^{\prime }<22$。在图G中有 $M:=M^{\prime }+\left\{v_1{w}_1,v_2{w}_2,z_1{z}_3,z_2{z}_4,{z^{\prime }}_{3}x,{z^{\prime }}_4{x}^{\prime }\right\}$，于是在图G中有：

$\begin{array}{c}\gamma \left(G\right)\le \frac{7n^{\prime }}{10}-\frac{m^{\prime }}{5}+6\le \frac{7}{10}\left(n-15\right)-\frac{1}{5}\left(m-22\right)+6\\ <\frac{7n}{10}-\frac{m}{5}\end{array}$

矛盾。

现在不妨令 $d\left(v_1\right)=3,d\left(v_2\right)=2$，则设点 $v_1$ 的邻居是点 ${w^{\prime }}_1$，点 $v_2$ 的邻居是点 $w_2$。若 $d\left(w_1\right)=3$，则设点 $w_1$ 的邻居是点 $z_1,{z^{\prime }}_1$，因为图G不包含 $T^{\ast }$，则点 ${w^{\prime }}_1$ 与点 $z_1,{z^{\prime }}_1$ 互为邻居。根据引理2可知，点 $z_1$ 有一个邻居为点x。因为图G不包含 $T^{\ast }$，则点 ${z^{\prime }}_1$ 与点x相互接连。若 $d\left(w_2\right)=2$，则设点 $w_2$ 的邻居为点 $z_2$。如果点 $z_2$ 与点x相互接连，则图G如下所示(图4)，可知图G并非反例。

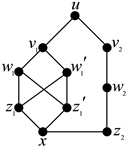
Figure 4. The graphs G in the case that vertext $z_2$ is adjacent to vertex x. Note that $\left\{u{v}_1,w_1{z}_1,z_{1}x,v_2{w}_2\right\}$ is a maximal matching of G, which implies $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

图4. 图G在点 $z_2$ 与点x相互接连的情况下。 $\left\{u{v}_1,w_1{z}_1,{z^{\prime }}_{1}x,v_2{w}_2\right\}$ 是其一个极大匹配，可知 $\gamma \left(G\right)<\frac{7n}{10}-\frac{m}{5}$

故点 $z_2$ 不与点x相互接连，根据引理2知，点x有一个邻居为点y。若令： $G^{″}=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,w_2,z_1,{z^{\prime }}_1,x,y\right\}$，则有： $n-n^{″}=10$， $m-m^{″}\le 15$， $M:=M^{″}+\left\{v_1{w}_1,v_2{w}_2,{w^{\prime }}_1{z^{\prime }}_1,xy\right\}$。于是在图G中有：

$\gamma \left(G\right)\le \frac{7n^{″}}{10}-\frac{m^{″}}{5}+4\le \frac{7}{10}\left(n-10\right)-\frac{1}{5}\left(m-15\right)+4=\frac{7n}{10}-\frac{m}{5}$

矛盾。

若 $d\left(w_1\right)=d\left(w_2\right)=3$，则根据图G不含 $T^{\ast }$ 和引理2可知，点 $w_2$ 有两个邻居为点 $z_2,{z^{\prime }}_2$，点 $z_2$ 有两个邻居为点 $z_3,{z^{\prime }}_3$，其中点 ${z^{\prime }}_2$ 与点 $z_3,{z^{\prime }}_3$ 相互接连，点 $z_3$ 有邻居点 $z_4$，点 ${z^{\prime }}_3$ 则与点 $z_4$ 相互接连。如果点x与点 $z_4$ 相互接连，则图G为I类图中的图b。若点x不与点 $z_4$ 相互接连，根据引理2可知，点x有一个邻居为点 $x^{\prime }$，点 $z_4$ 有一个邻居为点 ${z^{\prime }}_4$。现在考虑点 $x^{\prime }$ 和点 ${z^{\prime }}_4$ 的度数。由于对称性，有以下三种情形。

情形1 $d\left(x^{\prime }\right)=d\left({z^{\prime }}_4\right)=2$

设点 $x^{\prime }$ 的邻居是点 $a_1$，点 ${z^{\prime }}_4$ 的邻居是点 $b_1$。若令： $G^{\prime }=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,w_2,z_1,{z^{\prime }}_1,x,x^{\prime },a_1,z_2,{z^{\prime }}_2,z_3,{z^{\prime }}_3,z_4,{z^{\prime }}_4,b_1\right\}$ 则 $n-n^{\prime }=18$， $m-m^{\prime }<27$， $M:=M^{\prime }+\left\{u{v}_2,w_1{z}_1,{w^{\prime }}_1{z^{\prime }}_1,x^{\prime }{a}_1,z_2{z}_3,{z^{\prime }}_2{z^{\prime }}_3,{z^{\prime }}_4{b}_1\right\}$，在图G中有：

$\gamma \left(G\right)\le \frac{7n^{\prime }}{10}-\frac{m^{\prime }}{5}+7\le \frac{7}{10}\left(n-18\right)-\frac{1}{5}\left(m-27\right)+7<\frac{7n}{10}-\frac{m}{5}$

矛盾。

情形2 $d\left(x^{\prime }\right)=3$ 或 $d\left({z^{\prime }}_4\right)=3$

点 $x^{\prime },{z^{\prime }}_4$ 中有一个为3度点，不妨假设 $d\left(x^{\prime }\right)=3$。设点 $x^{\prime }$ 有两个邻居点 $a_1,{a^{\prime }}_1$，点 ${z^{\prime }}_4$ 有邻居点 $b_1$。因为图G中不包含 $T^{\ast }$，点 $a_1$ 或者点 ${a^{\prime }}_1$ 不能与点 $b_1$ 相互接连。由引理1可知，点 $a_1$ 有邻居点 $a_2$。因为图G不包含 $T^{\ast }$，故点 ${a^{\prime }}_1$ 与点 $a_2$ 邻接。由引理2知，点 $a_1$ 有邻居点 ${a^{\prime }}_2$，因为图G不包含 $T^{\ast }$，故点 ${a^{\prime }}_1$ 与点 ${a^{\prime }}_2$ 相互接连。又根据引理2知，点 $a_2$ 有一个邻居为点 $a_3$。因为图G不含 $T^{\ast }$，则点 ${a^{\prime }}_2$ 与点 $a_3$ 相互接连。因为图G为二部图，则点 $a_3$ 不与点 ${z^{\prime }}_4$ 相互接连。又由引理2可知，点 $a_3$ 有一个邻居为点 ${a^{\prime }}_3$。若令 $G^{″}=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,z_1,{z^{\prime }}_1,x,x^{\prime },a_1,{a^{\prime }}_1,a_2,{a^{\prime }}_2,a_3,{a^{\prime }}_3,w_2,z_2,{z^{\prime }}_2,z_3,{z^{\prime }}_3,z_4,{z^{\prime }}_4,b_1\right\}$，则图G与图 $G^{\prime }$ 的点数、边数和极大匹配数目存在以下关系： $n-n^{″}=23$， $m-m^{″}\le 35$， $M:=M^{″}+\left\{u{v}_2,w_1{z}_1,{w^{\prime }}_1{z^{\prime }}_1,x^{\prime }{a}_1,{a^{\prime }}_1{a^{\prime }}_2,a_3{a^{\prime }}_3,z_2{z}_3,{z^{\prime }}_2{z^{\prime }}_3,{z^{\prime }}_4{b}_1\right\}$。于是在图G中有：

$\gamma \left(G\right)\le \frac{7n^{″}}{10}-\frac{m^{″}}{5}+9\le \frac{7}{10}\left(n-23\right)-\frac{1}{5}\left(m-35\right)+9<\frac{7n}{10}-\frac{m}{5}$

矛盾。

情形3 $d\left(x^{\prime }\right)=d\left({z^{\prime }}_4\right)=3$

设点 $x^{\prime }$ 的邻居是点 $a_1,{a^{\prime }}_1$，点 ${z^{\prime }}_4$ 的邻居是点 $b_1,{b^{\prime }}_1$。因为图G中不含 $T^{\ast }$，故点 $a_1,{a^{\prime }}_1$ 不能与 $b_1,{b^{\prime }}_1$ 相互接连。由引理1可知，点 $a_1$ 有一个邻居为点 $a_2$，点 $b_1$ 有一个邻居为点 $b_2$，由图G不包含 $T^{\ast }$ 和引理2可知，点 ${a^{\prime }}_1$ 与点 $a_2,{a^{\prime }}_2$ 相互接连，点 $a_2,{a^{\prime }}_2$ 有公共的邻居点 $a_3$，点 $a_3$ 有邻居点 ${a^{\prime }}_3$，点 ${b^{\prime }}_1$ 与点 $b_2,{b^{\prime }}_2$ 相互接连，点 $b_2,{b^{\prime }}_2$ 有公共的邻居点 $b_3$。由引理1知，点 $b_3$ 有一个邻居为点 ${b^{\prime }}_3$。若令： $G^{‴}=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,z_1,{z^{\prime }}_1,x,x^{\prime },a_1,{a^{\prime }}_1,a_2,{a^{\prime }}_2,a_3,{a^{\prime }}_3,w_2,z_2,{z^{\prime }}_2,z_3,{z^{\prime }}_3,z_4,{z^{\prime }}_4,b_1,{b^{\prime }}_1,b_2,{b^{\prime }}_2,b_3,{b^{\prime }}_3\right\}$ 则 $n-n^{‴}=28$， $m-m^{‴}\le 43$， $M:=M^{‴}+\left\{u{v}_2,w_1{z}_1,{w^{\prime }}_1{z^{\prime }}_1,x^{\prime }{a}_1,{a^{\prime }}_1{a}_2,a_3{a^{\prime }}_3,z_2{z}_3,{z^{\prime }}_2{z^{\prime }}_3,{z^{\prime }}_4{b}_1,{b^{\prime }}_1{b}_2,b_3{b^{\prime }}_3\right\}$。于是在图G有：

$\gamma \left(G\right)\le \frac{7n^{‴}}{10}-\frac{m^{‴}}{5}+11\le \frac{7}{10}\left(n-28\right)-\frac{1}{5}\left(m-43\right)+11<\frac{7n}{10}-\frac{m}{5}$

矛盾。

说明了 $d\left(v_1\right)=d\left(v_2\right)=3$。设点 $v_1$ 的邻居是点 ${w^{\prime }}_1$，点 $v_2$ 的邻居是点 ${w^{\prime }}_2$，点 $w_1$ 的邻居是点 $z_1$，点 $w_2$ 的邻居是点 $z_2$。若 $m-m^{\prime }=8$，则说明 $d\left(w_1\right)=d\left(w_2\right)=2$。因为图G中不包含 $T^{\ast }$，则点 ${w^{\prime }}_1$ 与点 $z_1$ 相互接连，点 ${w^{\prime }}_2$ 与点 $z_2$ 相互接连，在四圈 $v_1{w}_1{z}_1{w^{\prime }}_1{v}_1,v_2{w}_2{z}_2{w^{\prime }}_2{v}_2$ 中，点 $w_1$ 与点 $w_2$ 均为2度点，与引理2矛盾。故 $m-m^{\prime }\ge 9$，于是 $d\left(v_i\right)=d\left(w_1\right)=3\left(i\in \left[1,2\right]\right)$。设点 $v_i$ 的邻居为点 $w_i,{w^{\prime }}_i$，点 $w_1$ 的邻居为点 $z_1,{z^{\prime }}_1$。因为图G中不含 $T^{\ast }$，故点 ${w^{\prime }}_1$ 与点 $z_1,{z^{\prime }}_1$ 相互接连。又根据引理2可知，点 $z_1$ 与点 ${z^{\prime }}_1$ 有公共的邻居点x。由引理1，设点x的邻居为点y，设点 $w_2$ 的邻居为点 $z_2$，因为图G不包含 $T^{\ast }$，则点 ${w^{\prime }}_2$ 与点 $z_2$ 相互接连。根据引理2可设点 $w_2$ 的邻居为 ${z^{\prime }}_2$，因为图G中不含 $T^{\ast }$，故点 ${w^{\prime }}_2,{z^{\prime }}_2$ 相互接连，而且点 $z_2,{z^{\prime }}_2$ 均与点y不同。由上述可知，点 $z_2,{z^{\prime }}_2$ 也有公共的邻居点 $x^{\prime }$，点 $x^{\prime }$ 也有邻居点 $y^{\prime }$。若 $y=y^{\prime }$，则图G为I类图中的图b。又因为图G不含 $T^{\ast }$，则 $d\left(y\right)\ne 3$。因此 $y\ne y^{\prime }$，现在考虑点 $y,y^{\prime }$ 的度数。由对称性，有以下三种情形。

情形1 $d\left(y\right)=d\left(y^{\prime }\right)=2$

在此情况下，若令 $G^{\prime }=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,w_2,{w^{\prime }}_2,z_1,{z^{\prime }}_1,z_2,{z^{\prime }}_2,x,x^{\prime },y,y^{\prime }\right\}$，有 $n-n^{\prime }=15$， $m-m^{\prime }\le 22$， $M:=M^{\prime }+\left\{v_1{w^{\prime }}_1,w_1{z}_1,xy,v_2{w}_2,{w^{\prime }}_2{z^{\prime }}_2,x^{\prime }{y}^{\prime }\right\}$，则在图G中有：

$\gamma \left(G\right)\le \frac{7n^{\prime }}{10}-\frac{m^{\prime }}{5}+6\le \frac{7}{10}\left(n-15\right)-\frac{1}{5}\left(m-22\right)+6<\frac{7n}{10}-\frac{m}{5}$

矛盾。

情形2 $d\left(y\right)=3$ 或 $d\left(y^{\prime }\right)=3$

点 $y,y^{\prime }$ 中有一个点度数为3，不妨假设 $d\left(y\right)=3$。设点y的邻居为点 $a_1,{a^{\prime }}_1$。因为图G中不含 $T^{\ast }$，故点 $a_1,{a^{\prime }}_1$ 不与点 $y^{\prime }$ 相互接连。由引理1知，点 $a_1$ 有一个邻居为点 $a_2$。因为图G中不含 $T^{\ast }$，则点 ${a^{\prime }}_1$ 与点 $a_2$ 相互接连。由引理2和图G不包含 $T^{\ast }$ 可知，点 $a_1$ 有邻居点 ${a^{\prime }}_2$ 且点 ${a^{\prime }}_1$ 与点 ${a^{\prime }}_2$ 相互接连。由图G不含 $T^{\ast }$ 及引理2可知，点 ${a^{\prime }}_2$ 与点 ${a^{\prime }}_1$ 有公共的邻居点 $a_3$。若令 $G^{″}=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,w_2,{w^{\prime }}_2,z_1,{z^{\prime }}_1,z_2,{z^{\prime }}_2,x,x^{\prime },y,y^{\prime },a_1,{a^{\prime }}_1,a_2,{a^{\prime }}_2,a_3\right\}$，有 $n-n^{″}=20$， $m-m^{″}\le 30$， $M:=M^{″}+\left\{v_1{w^{\prime }}_1,w_1{z}_1,xy,{a^{\prime }}_1{a^{\prime }}_2,a_2{a}_3,v_2{w}_2,{w^{\prime }}_2{z^{\prime }}_2,x^{\prime }{y}^{\prime }\right\}$，则在图G中有：

$\gamma \left(G\right)\le \frac{7n^{″}}{10}-\frac{m^{″}}{5}+8\le \frac{7}{10}\left(n-20\right)-\frac{1}{5}\left(m-30\right)+8+\frac{7n}{10}-\frac{m}{5}$

矛盾。

情形3 $d\left(y\right)=d\left(y^{\prime }\right)=3$

设点y的邻居为点 $a_1,{a^{\prime }}_1$，点 $y^{\prime }$ 的邻居为点 $b_1,{b^{\prime }}_1$。因为图G中不含 $T^{\ast }$，故点 $a_1,{a^{\prime }}_1$ 不与点 $b_1,{b^{\prime }}_1$ 相互接连。根据引理2知，点 $a_1$ 有邻居点 $a_2$，点 $b_1$ 有邻居点 $b_2$，由图G不含 $T^{\ast }$ 及引理2可知，点 ${a^{\prime }}_1$ 与点 $a_2,{a^{\prime }}_2$ 相互接连，点 ${b^{\prime }}_1$ 与点 $b_2,{b^{\prime }}_2$ 相互接连，点 $a_2,{a^{\prime }}_2$ 有公共的邻居为点 $a_3$，点 $b_2,{b^{\prime }}_2$ 有公共的邻居点为 $b_3$。根据引理2可知，点 $a_3,b_3$ 有邻居分别为点 $a_4,b_4$。根据点 $a_4,b_4$ 的度数有以下两种情形。

情形3.1 点 $a_4,b_4$ 中至少有一个为2度点

不妨假设 $d\left(a_4\right)=2$，设点 $a_4$ 的邻居为点 $a_5$，若令 $G^{‴}=G-\left\{u,v_1,v_2,w_1,{w^{\prime }}_1,z_1,{z^{\prime }}_1,x,y,a_1,{a^{\prime }}_1,a_2,{a^{\prime }}_2,a_3,a_4,a_5,w_2,{w^{\prime }}_2,z_2,{z^{\prime }}_2,x^{\prime },y^{\prime },b_1,{b^{\prime }}_1,b_2,{b^{\prime }}_2,b_3,b_4\right\}$ 则有 $n-n^{‴}=28$， $m-m^{″}\le 43$， $M:=M^{‴}+\left\{u{v}_1,w_1{z}_1,{z^{\prime }}_{1}x,a_1{a}_2,{a^{\prime }}_1{a^{\prime }}_2,a_4{a}_5,{w^{\prime }}_2{z^{\prime }}_2,w_2{z}_2,y^{\prime }{b^{\prime }}_1,b_1{b}_2,b_3{b}_4\right\}$，则在图G中有：

$\gamma \left(G\right)\le \frac{7n^{‴}}{10}-\frac{m^{‴}}{5}+11\le \frac{7}{10}\left(n-28\right)-\frac{1}{5}\left(m-43\right)+11=\frac{7n}{10}-\frac{m}{5}$

矛盾。

情形3.2 $d\left(a_4\right)=d\left(b_4\right)=3$

设点 $a_4$ 的邻居为点 $a_5,{a^{\prime }}_5$，点 $b_4$ 的邻居为点 $b_5,{b^{\prime }}_5$，由图G不含 $T^{\ast }$ 和引理2可知，点 $a_5$ 有邻居点 $a_6,{a^{\prime }}_6$，点 ${a^{\prime }}_5$ 与点 ${a^{\prime }}_6$ 相互接连，且点 $a_6$ 与点 ${a^{\prime }}_6$ 有公共的邻居为点 $a_7$。同理，点 $b_5$ 有两个邻居为点 $b_6,{b^{\prime }}_6$，其中点 ${b^{\prime }}_5$ 与点 ${b^{\prime }}_6$ 相互接连，且点 $b_6$ 与点 ${b^{\prime }}_6$ 有公共的邻居为点 $b_7$。又由引理2可知，点 $a_7,b_7$ 的邻居分别为点 $a_8,b_8$。若令：

$\begin{array}{l}{G}^{‴}=G-\{u,v_1,v_2,w_1,{w^{\prime }}_1,z_1,{z^{\prime }}_1,x,y,a_1,{a^{\prime }}_1,a_2,{a^{\prime }}_2,a_3,a_4,a_5,{a^{\prime }}_5,a_6,{a^{\prime }}_6,a_7,{a^{\prime }}_7,a_8,w_2,{w^{\prime }}_2,\\ z_2,{z^{\prime }}_2,x^{\prime },y^{\prime },b_1,{b^{\prime }}_1,b_2,{b^{\prime }}_2,b_3,b_4,b_5,{b^{\prime }}_5,b_6,{b^{\prime }}_6,b_7\},\end{array}$

则有 $n-n^{‴}=38$， $m-m^{‴}=58$， $M:=M^{‴}+\left\{u{v}_1,{w^{\prime }}_1{z^{\prime }}_1,z_{1}x,a_1{a}_2,{a^{\prime }}_1{a^{\prime }}_2,a_4{a^{\prime }}_5,a_5{a}_6,a_7{a}_8,{w^{\prime }}_2{z^{\prime }}_2,w_2{z}_2,y^{\prime }{b^{\prime }}_1,b_1{b}_2,b_3{b}_4,{b^{\prime }}_5{b^{\prime }}_6,b_6{b}_7\right\}$ 则在图G中有：

$\gamma \left(G\right)\le \frac{7n^{‴}}{10}-\frac{m^{‴}}{5}+15\le \frac{7}{10}\left(n-38\right)-\frac{1}{5}\left(m-58\right)+15=\frac{7n}{10}-\frac{m}{5}$

矛盾。

3. 定理1的证明

证明 设uv是图G的任意一条边。令 $G^{\prime }=G-\left\{u,v\right\}$， $n^{\prime }$ 和 $m^{\prime }$ 是图G的点数和边数。则有： $n-n^{\prime }=2$， $m-m^{\prime }=\frac{3n}{2}-5$。因为在图 $G^{\prime }$ 的极大匹配中添加边 $\left\{uv\right\}$ 会成为图G的极大匹配，而且图 $G^{\prime }$ 中没有是三正则图的连通分量，由定理2有：

$\gamma \left(G\right)\le \frac{7}{10}\left(n-2\right)-\frac{1}{5}\left(\frac{3n}{2}-5\right)+1=\frac{2n+3}{5}$。

基金项目

国家自然科学基金NSFC (Grant number: 11801522)。

NOTES

^*第一作者。

^#通讯作者。