随机约束Liu回归的局部影响分析

Local Influence Analysis for the Liu Regression under Stochastic Linear Restrictions

摘要: 在进行回归诊断时，影响点的检测一直是统计学者们研究的一个热点问题，而大多数情况下变量之间会存在自相关性即复共线性，再利用普通最小二乘估计进行影响点的检测会掩盖或掩没一些影响点，得到某些误导性结论。因此，本文考虑利用随机约束Liu估计克服数据间存在复共线时对检测带来的影响，在随机约束Liu回归模型下通过Cook似然距离和Tsai、Billor和Loynes (TBL)的另一种似然距离两种局部影响分析方法来检测影响点，分别在三种扰动模型下得到了影响矩阵、影响曲率和梯度所需的计算公式。最后，通过Longley数据集说明了两种方法都能检测影响点。

Abstract: In regression diagnosis, the detection of influence points has always been a hot issue studied by statisticians. In most cases, there will be autocorrelation between variables, namely complex collinearity, and the detection of influence points by using ordinary least square estimation will cover up or conceal some influence points and get some misleading conclusions. Therefore, in this paper, we consider using random constrained Liu estimation to overcome the influence of complex collinear data on detection. Under the random constrained Liu regression model, two local impact analysis methods, Cook likelihood distance and another likelihood distance of Tsai, Billor and Loynes (TBL), are used to detect the influence points. The formulas of influence matrix, influence curvature and gradient are obtained under three disturbance models. Finally, Longley data set shows that both methods can detect influence points.

1. 引言

回归诊断是回归分析中的重要内容，其主要的任务就是检测、识别样本观测数据与统计模型存在偏离的数据点，一般常见的诊断方法有全局影响分析和局部影响分析。全局影响分析是对比完全删除某个样本观察值前后估计量的变化程度来度量相应观察值的影响程度 [1]，以此识别出影响点。局部影响分析是1986年Cook [2] 首次提出用于识别异常点和强影响点的研究方法，从似然函数出发，利用微分几何观点提出的曲率的概念，再引入微小扰动的思想，通过似然距离来度量数据点的影响。近年来，局部影响分析受到统计学者们的广泛关注和发展，许多诊断方法也相继提出，如Tsai [3]、Billor和Loynes [4] 提出了基于新的似然距离用斜率替代曲率的局部影响分析方法。Shi [5] 提出了通过定义广义Cook统计量的局部影响分析方法。在实际生活中，Belsley [6] 等学者研究发现普通最小二乘估计在进行回归诊断时会掩没一些影响点，为了克服复共线性带来的某些不好影响，许多学者考虑用有偏估计替代最小二乘估计来减轻在影响点检测时带来的负面影响。如Jahufer [7]、Jahufer [8]、Shi [9]、Billor [10] 等所做的研究。另一方面，引入约束限制也是克服复共线性的一种方法，如Paula [11] 研究了不等式约束下线性模型的局部影响分析，Liu [12] 研究了随机约束线性模型的局部影响分析，Yang [13] 等研究了等式约束下椭球线性模型的局部影响分析。

基于前人的研究，使得我们考虑线性模型受随机约束且变量之间存在复共线性时的局部影响分析，因此本文考虑随机约束Liu估计应用于局部影响分析中，并分别利用Cook似然距离方法和TBL方法，给出了在方差扰动、因变量扰动、自变量扰动这三种扰动下的诊断统计量。

2. 模型与估计

考虑线性模型

$y=X\beta +e$ (2.1)

其中y是 $n\times 1$ 的因变量，X是秩为p的 $n\times p$ 阶设计矩阵，e是 $k\times 1$ 随机误差向量，期望为 $E\left(e\right)=0$，协方差矩阵为 $Var\left(e\right)={\sigma }^2{I}_n$，其中 ${\sigma }^{\text{2}}$ 是已知常数， $I_n$ 为n阶单位矩阵。假定参数估计 $\beta$ 受如下随机约束

$r=R\beta +u$ (2.2)

其中r是 $q\times 1$ 的已知随机向量，R是秩为q的 $q\times p$ 阶已知矩阵且 $q\le p$，u是 $q\times 1$ 随机误差向量，期望为 $E\left(u\right)=0$，方差矩阵为 $Var\left(u\right)={\sigma }^{2}V$，V是 $q\times q$ 阶已知正定矩阵。

基于模型(2.1)和(2.2)，便于应用于局部影响分析中利用Marquardt [14] 提出的方法，得到随机约束Liu回归的增广模型：

$z=Z\beta +\epsilon$ (2.3)

这里

$z=\left[\begin{array}{c}y\\ r\\ d{\beta }_{ols}\end{array}\right],Z=\left[\begin{array}{c}X\\ R\\ I_p\end{array}\right],\epsilon =\left[\begin{array}{c}e\\ u\\ \xi \end{array}\right]$ (2.4)

z是的阶数为 $m\times 1$，Z的阶数为 $m\times p$， $\epsilon$ 的阶数为 $m\times 1$ 的随机误差向量，期望为 $E\left(\epsilon \right)=0$，协方差矩阵为 $Var\left(\epsilon \right)={\sigma }^{2}Q$， $Q=diag\left(I_n,V,I_p\right)$，且该模型的各随机误差分量间相互独立。

为了将局部影响方法应用到随机约束Liu估计中，我们给出随机约束Liu回归模型(2.3)参数估计 $\beta$ 、 ${\sigma }^{\text{2}}$ 的极大似然估计。因此，我们假设模型(2.3)的随机误差服从 $\epsilon ~N\left(0,{\sigma }^{2}Q\right)$ 的正态分布。

则对应的似然函数为

$L\left(\theta \right)=-\frac{m}{2}\ln 2\pi -\frac{m}{2}\ln {\sigma }^2-\frac{1}{2}\ln \left|Q\right|-\frac{1}{2{\sigma }^2}{\epsilon }^{\text{T}}{Q}^{-1}\epsilon$ (2.5)

其中 $\theta ={\left({\beta }^{\text{T}},{\sigma }^2\right)}^{\text{T}}$。

下面我们给出参数 $\beta$， ${\sigma }^{\text{2}}$ 的极大似然估计。

定理1 对于模型(2.3)我们有

$\hat{\beta }={\left(X^{\text{T}}X+R^{\text{T}}{V}^{-1}R+I_p\right)}^{-1}\left(X^{\text{T}}y+R^{\text{T}}{V}^{-1}r+d{\beta }_{ols}\right)$.

${\hat{\sigma }}^2=\frac{1}{m}\left[{\left(y-X\hat{\beta }\right)}^{\text{T}}\left(y-X\hat{\beta }\right)+{\left(r-R\hat{\beta }\right)}^{\text{T}}{V}^{-1}\left(r-R\hat{\beta }\right)+{\left(d{\beta }_{ols}-\hat{\beta }\right)}^{\text{T}}\left(d{\beta }_{ols}-\hat{\beta }\right)\right]$

证明：对 $L\left(\theta \right)$ 分别关于 ${\beta }_i$ 和 ${\sigma }^{\text{2}}$ 求导，得

$\frac{\partial L\left(\theta \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}{\epsilon }^{\text{T}}{Q}^{-1}{Z}_{,i}$, (2.6)

$\frac{\partial L\left(\theta \right)}{\partial {\sigma }^2}=-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}{\epsilon }^{\text{T}}{Q}^{-1}\epsilon$, (2.7)

其中 $Z_{,i}$ 表示矩阵Z的第i列。令(2.6)式为零得

$\text{0}={\epsilon }^{\text{T}}{Q}^{-1}Z={\left(\begin{array}{c}y-X\beta \\ r-R\beta \\ d{\hat{\beta }}_{ols}-\beta \end{array}\right)}^{\text{T}}\left(\begin{array}{ccc}{I}_n& & \\ & V^{-1}& \\ & & I_p\end{array}\right)\left(\begin{array}{c}X\\ R\\ I\end{array}\right)$

$\hat{\beta }={\left(X^{\text{T}}X+R^{\text{T}}{V}^{-1}R+I_p\right)}^{-1}\left(X^{\text{T}}y+R^{\text{T}}{V}^{-1}r+d{\hat{\beta }}_{ols}\right)$

同理，令(2.7)式为零，我们计算

${\hat{\sigma }}^{\text{2}}=\frac{\text{1}}{m}{\hat{\epsilon }}^{\text{T}}{Q}^{-1}\hat{\epsilon }$ (2.8)

易得

${\hat{\sigma }}^2=\frac{1}{m}\left[{\left(y-X\hat{\beta }\right)}^{\text{T}}\left(y-X\hat{\beta }\right)+{\left(r-R\hat{\beta }\right)}^{\text{T}}{V}^{-1}\left(r-R\hat{\beta }\right)+{\left(d{\beta }_{ols}-\hat{\beta }\right)}^{\text{T}}\left(d{\beta }_{ols}-\hat{\beta }\right)\right]$

其中 $\hat{\epsilon }=z-Z\hat{\beta }$，证毕。

3. 局部影响分析

为了评估各扰动模型的局部影响，我们现在推导Cook方法下的观测信息矩阵 $-H$ 和矩阵 $\Delta$，以及TBL方法的梯度G，以便我们得到最大影响曲率和最大斜率这两个重要的统计量。

3.1. 观测信息矩阵

为了进一步探讨随机约束Liu回归模型下的影响点检测，我们推导其模型的观测影响矩阵，将参数估计 $\theta$ 划分为 $\theta ={\left({\beta }^{\text{T}},{\sigma }^2\right)}^{\text{T}}$，对观测信息矩阵 $-H$ 也进行相应划分。

定理2 对随机约束Liu估计， $\left(p+1\right)\times \left(p+1\right)$ 阶矩阵

$-H=\left[\begin{array}{cc}\frac{1}{{\hat{\sigma }}^2}{Z}^{\text{T}}{Q}^{-1}Z& \frac{1}{{\hat{\sigma }}^4}{Z}^{\text{T}}{Q}^{-1}\left(z-Z\hat{\beta }\right)\\ \frac{1}{{\hat{\sigma }}^4}{\left(z-Z\hat{\beta }\right)}^{\text{T}}{Q}^{-1}Z& \frac{m}{2{\hat{\sigma }}^4}\end{array}\right]$ (3.1)

证明：对(2.6)式的 $\frac{\partial L\left(\theta \right)}{\partial {\beta }_i}$ 分别关于 ${\beta }_j$ 、 ${\hat{\sigma }}^2$ 求导得

$\frac{{\partial }^{2}L\left(\theta \right)}{\partial {\beta }_j\partial {\beta }_i}=-\frac{1}{{\sigma }^2}{Z}_{,j}^{\text{T}}{Q}^{-1}{Z}_{{}_{,i}}$, $i,j=1,2,\cdots ,p$

$\frac{{\partial }^{\text{2}}L\left(\theta \right)}{\partial {\sigma }^2\partial {\beta }_i}=-\frac{1}{{\sigma }^4}{\left(z-Z\beta \right)}^{\text{T}}{Q}^{-1}Z$, $i=1,2,\cdots ,p$

将其中的未知数取为 $\beta =\hat{\beta }$ 和 ${\sigma }^{\text{2}}={\hat{\sigma }}^{\text{2}}$ 时，即得到矩阵 $-H$ 的前行。再对(2.7)式 $\frac{\partial L\left(\theta \right)}{\partial {\sigma }^2}$ 关于 ${\beta }_j$ 和 ${\sigma }^2$ 分别求导，得

$\frac{{\partial }^{2}L\left(\theta \right)}{\partial {\beta }_j\partial {\sigma }^2}=-\frac{1}{{\sigma }^4}{\left(z-Z\beta \right)}^{\text{T}}{Q}^{-1}{Z}_{,j}$, $j=1,2,\cdots ,p$

$\frac{{\partial }^{2}L\left(\theta \right)}{\partial {\sigma }^2\partial {\sigma }^2}=\frac{m}{2{\sigma }^4}-\frac{1}{{\sigma }^6}{\left(z-Z\beta \right)}^{\text{T}}{Q}^{-1}\left(z-Z\beta \right)$.

在上两式中令 $\beta =\hat{\beta }$ 和 ${\sigma }^{\text{2}}={\hat{\sigma }}^{\text{2}}$，则得到 $-H$ 的最后一行。

特别地，利用(2.8)式可得

${\frac{{\partial }^{\text{2}}\left(\theta \right)}{\partial {\sigma }^2\partial {\sigma }^2}|}_{\left(\beta =\hat{\beta },{\sigma }^{\text{2}}={\hat{\sigma }}^{\text{2}}\right)}=-\frac{m}{2{\hat{\sigma }}^4}$

因此可以写成矩阵形式

$-\frac{\partial L\left(\theta |\omega \right)}{\partial \theta \partial \partial {\theta }^{\text{T}}}=\left[\begin{array}{cc}\frac{1}{{\hat{\sigma }}^2}{Z}^{\text{T}}{Q}^{-1}Z& \frac{1}{{\hat{\sigma }}^4}{Z}^{\text{T}}{Q}^{-1}Z\left(z-Z\hat{\beta }\right)\\ \frac{1}{{\hat{\sigma }}^4}{\left(z-Z\hat{\beta }\right)}^{\text{T}}{Q}^{-1}Z& \frac{m}{2{\hat{\sigma }}^4}\end{array}\right]$

证毕。

接下来，我们分别讨论关于方差的扰动、因变量的扰动和自变量的扰动下相应的诊断统计量。

3.2. 方差扰动模型

此处我们考虑方差的扰动。令 $W_{\omega }^{-1}=diag\left\{{\omega }_{11}^{-1},\cdots ,{\omega }_{nn}^{-1}\right\}$ 是 $n\times n$ 阶正定扰动矩阵且 ${\omega }_{ii}=1+{\omega }_i$， $i=1,2,\cdots ,n$。显然 $\omega ={\left({\omega }_1,\cdots ,{\omega }_n\right)}^{\text{T}}=0$，即 $W_0^{-1}=I$，对应于无扰动情形，此时 $L\left(\theta |W_0\right)=L\left(\theta \right)$。这种情形下，扰动的协方差矩阵是 $Q_{\omega }=diag\left\{W_{\omega }^{-1},V,I\right\}$。

扰动的对数似然函数为

$L\left(\theta \right)=-\frac{m}{2}\ln 2\pi -\frac{m}{2}\ln {\sigma }^2-\frac{1}{2}\ln \left|Q_{\omega }\right|-\frac{1}{2{\sigma }^2}{\epsilon }^{\text{T}}{Q}_{\omega }^{-1}\epsilon$ (3.2)

定理3 对随机约束Liu估计得 $\left(p+1\right)\times n$ 阶矩阵

$\Delta =\left[\begin{array}{c}\frac{1}{{\hat{\sigma }}^2}{X}^{\text{T}}D\left(\hat{e}\right)\\ \frac{1}{2{\sigma }^4}{\hat{e}}^{\text{T}}D\left(\hat{e}\right)\end{array}\right]$ (3.3)

其中 $i=1,\cdots ,p$， $j=1,2,\cdots ,n$， $x_{ji}$ 表示矩阵X的第i行第j列的元素， ${\hat{e}}_j$ 表示 $\hat{e}$ 的第j个元素。

证明：利用(3.2)式的对数似然函数可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=-\frac{1}{{\sigma }^2}{\epsilon }^{\text{T}}{Q}_{\omega }^{-1}{Z}_{,i}$, $i=1,2,\cdots ,p$.

进一步

$\begin{array}{c}\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}{\epsilon }^{\text{T}}\left(\begin{array}{ccc}{W}_{\omega }^{-1}& & \\ & V^{-1}& \\ & & I\end{array}\right)Z_{,i}\\ =\frac{1}{{\sigma }^2}\left(e_1\left(1+{\omega }_1\right),\cdots ,e_n\left(1+{\omega }_n\right),u^{\text{T}}{V}^{-1},{\xi }^{\text{T}}\right)Z_{,i}\\ =\frac{1}{{\sigma }^2}\left[{\displaystyle \underset{j=1}{\overset{n}{\sum }}{e}_j\left(1+{\omega }_j\right)x_{ji}+u^{\text{T}}{V}^{-1}{R}_{,i}+I{\xi }^{\text{T}}}\right]\end{array}$

其中， $R_{,i}$ 表示矩阵R的第i列， ${\xi }_i$ 表示 $\xi$ 的第i个元素。上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$ 、 $\omega =0$ 取值可得

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\beta }_i}|}_{\theta =\hat{\theta },\omega =0}=\frac{1}{{\hat{\sigma }}^2}{\hat{e}}_j{x}_{ji}$

其中 ${\hat{e}}_j=y_j-X_{j,}\hat{\beta }$， $X_{j,}$ 表示矩阵X的第j行。

又利用(3.2)式的对数似然函数可得

$\frac{\partial \left(\theta |\omega \right)}{\partial {\sigma }^2}=-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}{\epsilon }^{\text{T}}{Q}_{\omega }^{-1}\epsilon =-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}\left[{\displaystyle \underset{j=1}{\overset{n}{\sum }}{e}_j\left(1+{\omega }_j\right)e_j+u^{\text{T}}{V}^{-1}u+{\xi }^{\text{T}}\xi }\right]$

上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$ 、 $\omega =0$ 取值可得

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\sigma }^2}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\frac{1}{2{\sigma }^4}{\left(e_j\right)}^2$,

因此可以写成矩阵表示

${\frac{\partial L\left(\theta |\omega \right)}{\partial \theta \partial {\omega }^{\text{T}}}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\left[\begin{array}{c}\frac{1}{{\hat{\sigma }}^2}{X}^{\text{T}}D\left(\hat{e}\right)\\ \frac{1}{2{\sigma }^4}{\hat{e}}^{\text{T}}D\left(\hat{e}\right)\end{array}\right]$

证毕。

在TBL方法下，我们得

定理4对随机约束Liu回归模型得

$G={\left(\frac{1}{2}-\frac{1}{2{\hat{\sigma }}^2}{\left({\hat{e}}_{\text{1}}\right)}^2,\cdots ,\frac{1}{2}-\frac{1}{2{\hat{\sigma }}^2}{\left({\hat{e}}_n\right)}^2\right)}^{\text{T}}$ (3.4)

证明：利用(4.2)式的对数似然函数可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_j}=\frac{1}{2\left(1+{\omega }_i\right)}-\frac{1}{2{\sigma }^2}{e}_i^2$.

代入 $\theta =\hat{\theta }$ 、 $\omega =0$ 即得

${\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_i}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\frac{1}{2}-\frac{1}{2{\hat{\sigma }}^2}{\left({\hat{e}}_j\right)}^2$, $i=1,2,\cdots ,n$

证毕。

3.3. 响应变量的扰动模型

此处我们考虑让因变量y的扰动形式记为 $y+\omega$，其中扰动 $\omega ={\left({\omega }_1,\cdots ,{\omega }_n\right)}^{\text{T}}$。则无扰动的情形对应于 $\omega ={\left(0,\cdots ,0\right)}^{\text{T}}$，而扰动后的对数似然为

$L\left(\theta |\omega \right)=-\frac{m}{2}\ln 2\pi -\frac{m}{2}\ln {\sigma }^2-\frac{1}{2}\ln \left|Q\right|-\frac{1}{2{\sigma }^2}{\epsilon }_{\omega }^{\text{T}}{Q}^{-1}{\epsilon }_{\omega }$ (3.5)

其中 ${\epsilon }_{\omega }={\left(y^{\text{T}}+{\omega }^{\text{T}},r^{\text{T}},d{\hat{\beta }}_{ols}\right)}^{\text{T}}-Z\beta$。

定理5 对随机约束Liu回归模型得 $\left(p+1\right)\times n$ 阶矩阵

$\Delta =\left[\begin{array}{c}\frac{1}{{\hat{\sigma }}^2}{X}^{\text{T}}\\ \frac{1}{{\sigma }^4}{\hat{e}}^{\text{T}}\end{array}\right]$ (3.6)

证明：利用(3.5)式中的对数似然函数可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}\left(y+\omega -X\beta ,r-R\beta ,d{\hat{\beta }}_{ols}-\beta \right)Q^{-1}Z$, $i=1,2,\cdots ,p$

$\begin{array}{c}\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}\left(y_1+{\omega }_1-X_{1,}\beta ,\cdots ,y_n+{\omega }_n-X_{n,}\beta ,u^{\text{T}}{V}^{-1},{\xi }^{\text{T}}\right)Z_{,i}\\ =\frac{1}{{\sigma }^2}\left[{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left(y_j+{\omega }_j-X_{j,}\beta \right)x_{ji}+u^{\text{T}}{V}^{-1}{R}_{,i}+{\xi }_i}\right]\end{array}$

上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$， $\omega =0$ 取值可得

${\frac{{\partial }^{\text{2}}L(\theta |\omega )}{\partial {\omega }_j\partial {\beta }_i}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\frac{1}{{\hat{\sigma }}^2}{x}_{ji}$.

又利用(3.5)式的对数似然函数可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\sigma }^2}=-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}{\epsilon }_{\omega }^{\text{T}}{Q}^{-1}{\epsilon }_{\omega }=-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}\left[{\displaystyle \underset{j=1}{\overset{n}{\sum }}{e}_{\omega j}{e}_{\omega j}+u^{\text{T}}{V}^{-1}u+{\xi }^{\text{T}}\xi }\right]$

其中 $e_{\omega j}$ 是 $e_{\omega }$ 的第j个元素。上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$ 、 $\omega =0$ 取值可得

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\sigma }^2}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\frac{1}{{\hat{\sigma }}^4}{\hat{e}}_j$,

因此可写成矩阵形式

${\frac{\partial L\left(\theta |\omega \right)}{\partial \theta \partial {\omega }^{\text{T}}}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\left[\begin{array}{c}\frac{1}{{\hat{\sigma }}^2}{X}^{\text{T}}\\ \frac{1}{{\sigma }^4}{\hat{e}}^{\text{T}}\end{array}\right]$

证毕。

在TBL方法下，我们得

定理6 对随机约束Liu回归模型得

$G=-\frac{1}{{\hat{\sigma }}^2}\hat{e}$ (3.7)

证明：利用(3.5)式的对数似然函数可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_i}=-\frac{1}{{\sigma }^2}\left(y_i+{\omega }_i-X_{i,}\beta \right)$

代入 $\theta =\hat{\theta }$ 、 $\omega =0$ 即得

${\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_j}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=-\frac{1}{{\hat{\sigma }}^2}{\hat{e}}_i$, $i=1,2,\cdots ,n$,

证毕。

3.4. 解释变量的扰动模型

Cook (1986)指出当自变量之间存在复共线性时，自变量的微小扰动会影响最小二乘回归的结果。我们讨论自变量扰动令 $X_{\omega }=X+s\omega d$，则第t个自变量的扰动为 $X_{\omega }=X+s_t\omega d_t^{\text{T}}$，这里 $\omega ={\left({\omega }_1,\cdots ,{\omega }_n\right)}^{\text{T}}$ 表示n维的扰动向量，d为 $p\times 1$ 的向量，则 $d_t$ 为第t个分量为1、其余为0的向量，s为尺度因子，则 $s_t$ 用于解释X各列的不同的测量单位。显然无扰动的情形对于 $\omega ={\left(\text{0},\cdots ,0\right)}^{\text{T}}$，而扰动后的对数似然函数 $L\left(\theta |\omega \right)$ 为

$L\left(\theta |\omega \right)=-\frac{m}{2}\ln 2\pi -\frac{m}{2}\ln {\sigma }^2-\frac{1}{2}\ln \left|Q\right|-\frac{1}{2{\sigma }^2}{\epsilon }_{\omega }^{\text{T}}{Q}^{-1}\epsilon$ (3.8)

而这里的 ${\epsilon }_{\omega }$ 为

${\epsilon }_{\omega }={\left(y^{\text{T}},r^{\text{T}},I_p\right)}^{\text{T}}-Z_{\omega }\beta$, (3.10)

其中 $Z_{\omega }$ 表示将矩阵Z中X代替为 $X_{\omega }$ 得到的矩阵。

定理7对随机约束Liu估计模型，扰动设计矩阵的第t列得 $\left(p+1\right)\times n$ 阶矩阵

$\Delta =\left[\begin{array}{c}-\frac{s}{{\hat{\sigma }}^2}\left({\hat{\beta }}^{\text{T}}{X}^{\text{T}}-{\delta }_{it}{\hat{e}}^{\text{T}}\right)\\ -\frac{s}{{\hat{\sigma }}^4}\hat{\beta }{\hat{e}}^{\text{T}}\end{array}\right]$, $i=1,\cdots ,p$, $t=1,\cdots ,p$, ${\delta }_{it}=\{\begin{array}{cc}1& t=i\\ 0& t\ne i\end{array}$,

证明：利用(4.8)和(4.10)式可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}{\epsilon }_{\omega }^{\text{T}}{Q}^{-1}{Z}_{\omega ,i}$, $i=1,2,\cdots ,p$,

其中 $Z_{\omega ,i}$ 表示 $Z_{\omega }$ 的第i列。进一步

$\begin{array}{c}\frac{\partial L\left(\theta |\omega \right)}{\partial {\beta }_i}=\frac{1}{{\sigma }^2}\left(y_1-X_{\omega 1,}\beta ,\cdots ,y_n-X_{\omega n,}\beta ,u^{\text{T}}{V}^{-1},{\xi }^{\text{T}}\right)Z_{\omega ,i}\\ =\frac{1}{{\sigma }^2}\left[{\displaystyle \underset{s=1}{\overset{n}{\sum }}\left(y_s-{\displaystyle \underset{r=1,r\ne t}{\overset{p}{\sum }}{x}_{sr}{\beta }_r-\left(x_{st}+s_t{\omega }_s\right){\beta }_t}\right)x_{\omega si}+u^{\text{T}}{V}^{-1}{R}_{,i}+{\xi }^{\text{T}}{I}_p}\right]\end{array}$

$x_{\omega si}$ 是 $X_{\omega }$ 的第s行第i列的元素。

将上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$ 、 $\omega =0$ 计算得

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\beta }_i}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\{\begin{array}{l}\begin{array}{cc}-\frac{s_t}{{\hat{\sigma }}^2}{\hat{\beta }}_t{x}_{ji},& t\ne i\end{array}\\ -\frac{s_t}{{\hat{\sigma }}^2}{\hat{\beta }}_t{x}_{ji}+\frac{1}{{\hat{\sigma }}^2}{s}_t\left(y_j-X_{j,}\hat{\beta }\right)\begin{array}{cc},& t=i\end{array}\end{array}$,

此式可合写为

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\beta }_i}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=-\frac{s_t}{{\hat{\sigma }}^2}{\hat{\beta }}_t{x}_{ji}+\frac{1}{{\hat{\sigma }}^2}{\delta }_{it}{s}_t\left(y_j-X_{j,}\hat{\beta }\right)=-\frac{s_t}{{\hat{\sigma }}^2}{\hat{\beta }}_t{x}_{ji}+\frac{1}{{\hat{\sigma }}^2}{\delta }_{it}{s}_t{\hat{e}}_j$

又由(3.8)和(3.10)式算得

$\begin{array}{c}\frac{\partial L\left(\theta \omega \right)}{\partial {\sigma }^2}=-\frac{m}{2{\sigma }^2}+\frac{1}{2{\hat{\sigma }}^4}{\epsilon }_{\omega }^{\text{T}}{Q}^{-1}{\epsilon }_{\omega }\\ =-\frac{m}{2{\sigma }^2}+\frac{1}{2{\sigma }^4}\left[{\displaystyle \underset{s=1}{\overset{n}{\sum }}{\left(y_s-{\displaystyle \underset{r=1,r\ne t}{\overset{p}{\sum }}{x}_{sr}{\beta }_r-\left(x_{st}+s_t{\omega }_s\right){\beta }_t}\right)}^2}+u^{\text{T}}{V}^{-1}u+{\xi }^{\text{T}}\xi \right]\end{array}$

上式关于 ${\omega }_j$ 求导并在 $\theta =\hat{\theta }$ 、 $\omega =0$ 取值可得

${\frac{{\partial }^{2}L\left(\theta |\omega \right)}{\partial {\omega }_j\partial {\sigma }^2}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=-\frac{s_t}{{\hat{\sigma }}^4}\left(y_j-X_{j,}\hat{\beta }\right){\hat{\beta }}_t=-\frac{s_t}{{\hat{\sigma }}^4}{\hat{e}}_j$,

因此可以写成矩阵形式

${\frac{\partial L\left(\theta |\omega \right)}{\partial \theta \partial {\omega }^{\text{T}}}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\left[\begin{array}{c}-\frac{s}{{\hat{\sigma }}^2}\left(\hat{\beta }{X}^{\text{T}}-{\delta }_{it}{\hat{e}}^{\text{T}}\right)\\ -\frac{s}{{\hat{\sigma }}^4}\hat{\beta }\hat{e}\end{array}\right]$

证毕。

在TBL方法下，我们得到

定理8 对随机约束Liu估计模型，扰动设计矩阵的第t列得

$G=\frac{s_t{\hat{\beta }}_t}{{\hat{\sigma }}^2}\hat{e}$

证明：利用(3.8)和(3.10)式可得

$\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_j}=\frac{s_t}{{\sigma }^2}\left(y_i-\left(X_{i,}+s_t{\omega }_t{d}_t^{\text{T}}\right)\beta \right){\beta }_t$

代入 $\theta =\hat{\theta }$ 、 $\omega =0$ 即得

${\frac{\partial L\left(\theta |\omega \right)}{\partial {\omega }_i}|}_{\left(\theta =\hat{\theta },\omega =0\right)}=\frac{s_t}{{\hat{\sigma }}^2}{\hat{e}}_i{\hat{\beta }}_t$, $i=1,2,\cdots ,n$

证毕。

4. 实证分析

为了验证在Cook和TBL的基础上提出的新方法的合理性，考虑引入Longley [15] 宏观经济数据集来检验该新方法。这组数据由就业、国民生产总值内含平减物价、国民生产总值、失业数、军事武装部队规模、14岁及以上的非机构人口、年份7个指标组成。其中y是总派生就业率，x₁是GNP隐含价格平减指数，x₂是国民生产总值，x₃是失业率，x₄是武装力量的规模，x₅是14岁及以上的非机构人口，x₆是年份。Belsley等人利用最大特征值与最小特征值的比值计算得到条件数值，该数据集下的条件数为43275，说明Longley宏观经济数据集变量之间存在很强的共线性。

Cook (1977) [16] 利用Longley基于最小二乘估计的全局影响分析，从大到小依次检测出5、16、4、10、15为影响点(本文所有排序都是从大到小)，Walker和Birch [17] 基于岭估计的全局影响分析，检测出16、10、4、15、1为影响点，容易见两种方法检测出的影响点有较大差异，这是因为最小二乘估计在回归诊断时的不稳定性导致的。此外，取岭参数 $k=0.0002$，Shi和Wang考虑岭估计局部影响分析，检测出10、4、15、16、1为影响点，当数据集复共线性很强时，Liu提出了Liu估计，该估计在克服复共线性和均方误差准则皆优于岭估计。考虑其优良性，取Liu参数 $d=0.9724$，Jahufer和Chen (2010)利用Liu估计局部影响分析，检测出4、10、1、5、6为影响点，

局部影响分析方法探测到了基于Liu估计下的影响点，Zhang (2010)基于Liu估计局部影响分析，在方差扰动、响应变量扰动、解释变量扰动三种模型下，检测出4、5、6、10、11、13为影响点。同样我们选择该数据集，以此来和前人的检测结果进行比较。因此，选择Ozkale (2009) [18] 选择的数据点2、3 来构成随机约束的(3.5)式。首先对数据点2、3进行标准化处理，所以有

$R=\left[\begin{array}{cccccc}-0.3154& -0.3332& -0.2399& -0.4269& -0.3263& -0.3525\\ -0.3226& -0.3368& 0.3150& -0.3676& -0.2840& -0.2983\end{array}\right]$

$r=\left[\begin{array}{c}-0.3084\\ -0.3783\end{array}\right]$

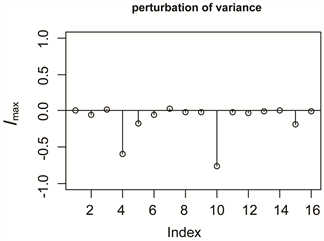
在方差扰动下，取Liu参数 $d=0.9$，使用Cook的方法所得到的 $l_{\max }$ 向量的检测结果见图1(a)，影响最大的分量为10，4。使用TBL所得到的 $l_{\max }^{\ast }$ 向量的检测结果见图1(b)，同样影响最大的分量为10，4。这说明在方差扰动下随机约束Liu回归在Cook方法和TBL方法探测到的影响点没有明显差异。

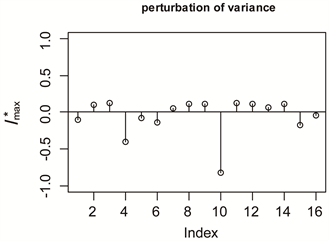(a) (b)

Figure 1. (a) is the index graph of $l_{\max }$ under variance disturbance; (b) is the index graph of $l_{\max }^{\ast }$ under variance disturbance

图1. (a)为方差扰动下 $l_{\max }$ 的指标图；(b)为方差扰动下 $l_{\max }^{\ast }$ 的指标图

在响应变量扰动下，取Liu参数 $d=0.9$，在图2(a)中，基于Cook方法的最大分量 $l_{\max }$ 依次对应点10、4、15、6、1。在图2(b)中，基于TBL方法的最大分量 $l_{\max }^{\ast }$ 依次对应点10、4、15、6、1。根据Schwarzmann [19] 无偏估计下 $l_{\max }$ 正比于残差向量，通过本文定理6知 $l_{\max }^{\ast }$ 是正比于残差向量的，易见两图 $l_{\max }^{\ast }$ 、 $l_{\max }$ 几乎完全一样，即他们是成比例的。说明随机约束Liu回归下 $l_{\max }$ 和 $l_{\max }^{\ast }$ 是正比于残差向量的

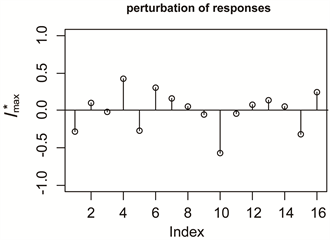(a) (b)

Figure 2. (a) is the index graph of $l_{\max }$ under the disturbance of response variable; (b) is the index graph of $l_{\max }^{\ast }$ under the disturbance of response variable

图2. (a)为响应变量扰动下 $l_{\max }$ 的指标图；(b)为响应变量扰动下 $l_{\max }^{\ast }$ 的指标图

在单个解释变量扰动下。同样取Liu参数 $d=0.9$，基于Cook方法的最大分量 $l_{\max }$，见图3(b)、图3(c)、图3(e)的检测结果，发现扰动解释变量x₂、x₃、x₆的影响点都为10、4、15、6、1，见图3(a)的检测结果，发现扰动解释变量x₁的影响点为10、4、1、15、6，见图3(d)的检测结果，发现扰动解释变量的x₄的影响点为10、4、15、5、6，见图3(f)的检测结果，发现扰动解释变量的x₅的影响点为10、4、6、5、15，易见自变量的改变会导致检测结果的改变。基于TBL的最大分量 $l_{\max }^{\ast }$，见图4(a)~(e)的检测结果，发现扰动解释变量扰动x₁、x₂、x₃、x₄、x₅、x₆都的影响点都为10、4、15、6、1。与其他学者的方法相比，检测结果有三个以上是相同的，说明本文基于随机约束下Liu估计提出的局部影响分析方法的合理性。

两种方法也反映了Cook方法更能为我们提供更多信息，同时，通过检测结果发现我们选取的数据点2、3不是影响点，这也说明了我们选取的约束条件不同也会对我们的结果产生负面影响。在这种情形下我们检测到的结论和前人探测到的结论是可比较的。我们也考虑不同的Liu参数d值检测出的影响点也不完全相同，说明Liu参数d的选取会影响我们的检测结果。

(a) (b) (c) (d) (e) (f)

Figure 3. (a)~(f) is the index graph of $l_{\max }$ disturbed by a single explanatory variable

图3. (a)~(f)为单个解释变量扰动下 $l_{\max }$ 的指标图

(a) (b) (c) (d) (e) (f)

Figure 4. (a)~(f) is the index graph of $l_{\max }^{\ast }$ disturbed by a single explanatory variable

图4. (a)~(f)为单个解释变量扰动下 $l_{\max }^{\ast }$ 的指标图

5. 结论

本文研究了具有随机线性约束Liu回归中的影响诊断方法。利用Marquardt (1970)的方法得到了极大似然随机约束Liu估计，我们在三种扰动模型下导出了Cook方法的观测信息矩阵 $-H$ 和 $\Delta$，以及TBL方法的梯度G。从而得到Cook方法的 $C_{\max }$ 和 $l_{\max }$，以及扰动模型下TBL方法的 $S_{\max }^{\ast }$ 和 $l_{\max }^{\ast }$。最后，通过数据集进行了验证，说明本文所提出的理论与方法的合理性。