基于MSSOR求解信号恢复问题的ADMM算法

ADMM Algorithm for Solving Signal Recovery Problem Based on MSSOR

摘要: 基于改进的对称逐次超松弛(MSSOR)方法，本文针对信号恢复问题提出了一种交替方向乘子(ADMM)法。该方法是一种内外部迭代相结合的方法，其中内部迭代为MSSOR方法，外部迭代为ADMM方法。在适当条件下，证明了所提算法的全局收敛性，数值结果表明，该方法既能在较短的时间内恢复信号，又能提高重构图像的质量。

Abstract: Based on the improved symmetric successive overrelaxation (MSSOR) method, an alternating direction multiplier (ADMM) method is proposed to solve the signal recovery problem. The method is a combination of internal and external iterations, in which the internal iteration is MSSOR method and the external iteration is ADMM method. Under appropriate conditions, the global convergence of the proposed algorithm is proved. Numerical results show that the proposed method can not only restore the signal in a short time, but also improve the quality of the reconstructed image.

1. 引言

在信号处理过程中，信号恢复的两项关键技术是压缩感知(CS)和图像去模糊 [1] [2] [3]。具体来说，对于稀疏或可压缩信号，CS可以在不影响重构质量的情况下显著减少测量次数 [4] [5]。对于模糊图像，图像去模糊可以保证恢复真实图像 [6]。近年来，信号恢复已经成为医学、天文图像恢复、文件恢复和编码等应用领域的重要工具 [7] [8]。

设x是稀疏的或近似稀疏的原始信号， $A\in R^{m\times n}\left(m\ll n\right)$ 是一个线性算子，对于给定的观测值 $b\in R^m$，满足 $b=Ax$，我们需要通过求解线性方程组 $Ax=b$ 来重构原始信号x，由于 $A\in R^{m\times n}\left(m\ll n\right)$ 在这个线性系统中是欠定或者病态的，因此寻求此线性系统的解一般来说比较困难 [9]。根据压缩感知的基本理论，重构原始信号x需要求解如下的连续优化问题 [10] [11]：

$\underset{x}{\min }\left\{{\Vert x\Vert }_1:Ax=b\right\}.$ (1)

考虑到实际中噪声的存在，(1)的约束可以放宽，重新表述为以下受惩罚的最小二乘问题：

$\underset{x}{\min }\left\{\tau {\Vert x\Vert }_1+\frac{1}{2}{\Vert Ax-b\Vert }_2^2\right\},$ (2)

式中 $\tau$ 为平衡参数。

为了求解模型(2)，学者们提出了多种迭代方法，其中迭代收缩阈值法(IST)和快速迭代收缩阈值法(FISTA) [12] [13] 因其简单高效而最受欢迎。另外，文献 [14] 提出了一种不动点连续搜索方法，并引入了一种基于Barzilai-Borwein步长的非单调线搜索加速技术 [15]。Figueiredo提出了梯度投影方法来解决稀疏重建问题 [16]，Xiao等分别提出了求解问题(2)的共轭梯度投影法和谱梯度法 [17] [18]。由一个近似等价问题的驱动，文献 [19] 进一步将修正谱共轭梯度投影法推广到求解方程组。研究表明， [19] 中的算法在解决大规模非线性单调方程组中明显优于以上的算法。

本文将问题(2)转化为一个等价的凸二次规划问题，并给出一种改进的对称逐次超松弛(MSSOR)的交替方向乘子(ADMM)算法。数值实验表明，在处理信号恢复问题上，相较于类似的方法，本文的算法是更有效的。

2. 预备工作

对于任意向量 $x\in R^n$，令 $x=u-v$， $u\left(\in R^n\right)\ge 0$， $v\left(\in R^n\right)\ge 0$， ${\left[x_i\right]}_{+}=\max \left\{0,x_i\right\}$， $u_i={\left(x_i\right)}_{+}$， $v_i={\left(-x_i\right)}_{+}$，其中 $i=1,2,\cdots ,n$，考虑到，x的 $l_1$ -范数表示为 ${\Vert x\Vert }_1=e_n^{\text{T}}u+e_n^{\text{T}}v$，其中 $e_n$ 表示一个所有元素都为1的n维向量用，因此问题(2)等价于：

$\begin{array}{l}\underset{u,v}{\min }\frac{1}{2}{\Vert A\left(u-v\right)-b\Vert }^2+\tau e_n^{\text{T}}u+\tau e_n^{\text{T}}v,\\ \text{s}\text{.t}\text{.}u\ge 0,v\ge 0,u^{\text{T}}v=0.\end{array}$ (3)

通过惩罚法，(3)式等价于：

$\begin{array}{l}\underset{u,v}{\min }\frac{1}{2}{\Vert A\left(u-v\right)-b\Vert }^2+\tau e_n^{\text{T}}u+\tau e_n^{\text{T}}v,\\ \text{s}\text{.t}\text{.}u\ge 0,v\ge 0,u^{\text{T}}v=0.\end{array}$ (4)

其中 $\delta$ 是一个惩罚系数，我们将上式展开计算后，问题(4)可以等价表述为：

$\underset{z\ge 0}{\min }\frac{1}{2}{z}^{\text{T}}\left(H+D\right)z+c^{\text{T}}z.$ (5)

其中，

$\begin{array}{l}z=\left[\begin{array}{c}u\\ v\end{array}\right],y=A^{\text{T}}b,c=\tau e_{2n}+\left[\begin{array}{c}-y\\ y\end{array}\right],\\ H=\left[\begin{array}{cc}{A}^{\text{T}}A& -A^{\text{T}}A\\ -A^{\text{T}}A& A^{\text{T}}A\end{array}\right],D=\left[\begin{array}{cc}0& \delta E_n\\ 0& 0\end{array}\right].\end{array}$

根据 [18] 中的证明可知 $H,D$ 皆为半正定的矩阵，因此(5)是一个凸二次规划问题。

下面我们考虑使用ADMM方法来求解问题(5)，令 $\mathcal{X}$， $\mathcal{Y}$ 和 $\mathcal{Z}$ 为三个有限维实欧氏空间，每个实欧氏空间都有内积 $\langle \cdot ,\cdot \rangle$ 及其范数 $\Vert \cdot \Vert$，令 $f:\mathcal{Y}\to \left(-\infty ,+\infty \right],g:\mathcal{Z}\to \left(-\infty ,+\infty \right]$ 是两个闭的凸函数，对于如下可分的凸优化问题 [20] [21]：

$\underset{y\in \mathcal{Y},z\in \mathcal{Z}}{\min }\left\{f\left(y\right)+g\left(z\right)\text{s}\text{.t}\text{.}{\mathcal{A}}^{*}y+{\mathcal{B}}^{*}z=c\right\},$ (6)

其中 $c\in \mathcal{X}$ 是给定的数，线性映射 ${\mathcal{A}}^{*}$ 和 ${\mathcal{B}}^{*}$ 为伴随算子，任意 $\left(x,y,z\right)\in \mathcal{X}\times \mathcal{Y}\times \mathcal{Z}$，令 $\sigma >0$ 是给定的罚参数，得到问题(6)的增广拉格朗日函数为 [22]：

${\mathcal{L}}_{\sigma }\left(y,z;x\right):=f\left(y\right)+g\left(z\right)+\langle x,{\mathcal{A}}^{*}y+{\mathcal{B}}^{*}z-c\rangle +\frac{\sigma }{2}{\Vert {\mathcal{A}}^{*}y+{\mathcal{B}}^{*}z-c\Vert }^2,$ (7)

选取初始点 $\left(x^0,y^0,z^0\right)\in \mathcal{X}\times \text{dom}f\times \text{dom}g,\tau \in \left(0,+\infty \right)$，Glowinski，Marrocol，Gabay和Mercier的经典交替方向乘子法相应的求解步骤 [23] 如下：

$\{\begin{array}{l}{y}^{k+1}=\underset{y}{\arg \min }{\mathcal{L}}_{\sigma }\left(y,z^k;x^k\right),\\ z^{k+1}=\underset{z}{\arg \min }{\mathcal{L}}_{\sigma }\left(y^{k+1},z;x^k\right),\\ x^{k+1}=x^k+\tau \sigma \left({\mathcal{A}}^{\text{*}}{y}^{k+1}+{\mathcal{B}}^{\text{*}}{z}^{k+1}-c\right)\text{.}\end{array}$ (8)

交替方向乘子法(8)的收敛性分析由Gabay，Mercier，Glowinski和Fortin以及Glowinski [23] [24] 在不同的条件下给出。

本文将(5)置于ADMM的框架中，令 $M=H+D$，则原模型等价于解下面的最小化问题:

$\begin{array}{c}\{\begin{array}{l}\min f\left(z\right)=\frac{1}{2}{z}^{\text{T}}\left(H+D\right)z+c^{\text{T}}z=\frac{1}{2}M{z}^2+c^{\text{T}}z,\\ \text{subjectto}z\ge 0.\end{array}\end{array}$ (9)

设非负正交 $R_{+}^n$ 是具有非负分量的点的集合：

$R_{+}^n=\left\{x\in R^n:x_i\ge 0,i=1,2,\cdots ,n\right\}.$

设 $R_{+}^n$ 的指标函数为g：

$g\left(x\right)=0$，当 $x\in R_{+}^n$ 时；否则， $g\left(x\right)=+\infty$。

给定一个正对角矩阵 $\Lambda$，最小化问题(9)可以等价地写成：

$\{\begin{array}{l}\min f\left(z\right)+g\left(w\right),\\ \text{subjectto}\Lambda \left(z-w\right)=0,w\in R_{+}^n.\end{array}$ (10)

记(10)的拉格朗日函数为：

$L\left(z,w,\lambda \right)=f\left(z\right)+g\left(w\right)+{\lambda }^{\text{T}}\text{Λ}\left(w-z\right)+\frac{\rho }{2}{\Vert \text{Λ}\left(w-z\right)\Vert }^2.$

其中 $\rho >0$ 是惩罚参数。给定 $z^{\left(0\right)},{\lambda }^{\left(0\right)},w^{\left(0\right)}\in R^n$，ADMM的第k次迭代可通过如下步骤获得 [25]：

$\{\begin{array}{l}{z}^{\left(k+1\right)}=\underset{z\in R^n}{\arg \min }L\left(z,w^{\left(k\right)},{\lambda }^{\left(k\right)}\right),(11.1)\\ w^{\left(k+1\right)}=\underset{w\in R_{+}^n}{\arg \min }L\left(z^{\left(k+1\right)},w,{\lambda }^{\left(k\right)}\right),(11.2)\\ {\lambda }^{\left(k+1\right)}={\lambda }^{\left(k\right)}+\rho \Lambda \left(w^{\left(k+1\right)}-z^{\left(k+1\right)}\right).(\; 11.3\; )\end{array}$

问题(11.1)的求解公式如下：

$z^{\left(k+1\right)}={\left(M+\rho {\Lambda }^2\right)}^{-1}\left(\Lambda {\lambda }^{\left(k\right)}+\rho {\Lambda }^2{w}^{\left(k\right)}-c\right).$ (12)

同样，问题(11.2)的求解公式如下：

$w^{\left(k+1\right)}={\left(z^{\left(k+1\right)}-\frac{{\text{Λ}}^{-1}{\lambda }^{\left(k\right)}}{\rho }\right)}_{+}.$ (13)

这里 ${\left(﹒\right)}_{+}$ 表示集合 $R_{+}^n$ 上的投影，基于(12)和(13)式，由此我们可以给出求解问题(5)的具体算法：

由于(10)是一个目标函数是严格凸的凸规划问题，因此它有唯一的最优解。

而问题(11)等价于求 $\left(z^{*},w^{*},{\lambda }^{*}\right)\in R^n\times R_{+}^n\times R^n$，

$\left(M{z}^{*}+c\right)-\text{Λ}{\lambda }^{*}=0$ (14)

$\begin{array}{c}{\left(w-w^{*}\right)}^{\text{T}}\text{Λ}{\lambda }^{*}\ge 0,\forall w\in R_{+}^n\end{array}$ (15)

$z^{*}-w^{*}=0$ (16)

对于满足条件(14) (15) (16)的某些 ${\lambda }^{*}$， $\left\{z^{*},w^{*},{\lambda }^{*}\right\}$，以上算法生成的序列 $\left\{z^{\left(k\right)},w^{\left(k\right)}\right\}$ 收敛于 $\left\{z^{*},w^{*}\right\}$，此定理的类似证明见文献 [26]。

在算法1中，每次迭代k时，我们能得到线性方程组的精确解：

$\left(M+{\Lambda }^2\right)z^{\left(k+1\right)}=\Lambda {\lambda }^{\left(k\right)}+\rho {\Lambda }^2{w}^{\left(k\right)}-c$ (17)

但当问题较大且稀疏时，不容易直接求解(18)。这一困难促使我们使用更有效的迭代方法，如经典SOR方法或共轭梯度法来求解系统(18)，然而，对于实际问题，当使用迭代法时，很难控制内部迭代。我们使用一步MSSOR迭代来近似求解(18)，使用一种基于MSSOR的ADMM方法。

令 $M=D+L+U$，其中矩阵D，L和U分别为矩阵M的对角矩阵、严格下三角矩阵和严格上三角矩阵，具体形式为：

$M=\left[\begin{array}{cc}{A}^{\top }A& \\ & A^{\top }A\end{array}\right]+\left[\begin{array}{cc}0& 0\\ -A^{\top }A& 0\end{array}\right]+\left[\begin{array}{cc}0& \delta E_n-A^{\top }A\\ 0& 0\end{array}\right]=Q+L+U$

我们使用以下等式来求解等式(17)，其中 $\alpha \in \left(0,2\right)$ 为松弛参数：

$\{\begin{array}{l}\left(Q+\alpha L+\alpha \rho {\Lambda }^2\right)z^{\left(k+\frac{1}{2}\right)}=\left(\left(1-\alpha \right)Q+\alpha U\right)x^k+\alpha p^k;\\ \left(Q+\alpha U+\alpha \rho {\Lambda }^2\right)z^{k+1}=\left(\left(1-\alpha \right)Q+\alpha L\right)z^{k+\frac{1}{2}}+\alpha p^k.\end{array}$ (18)

在这里 $p^k=\text{Λ}{\lambda }^{\left(k\right)}+\rho {\text{Λ}}^2{w}^{\left(k\right)}-c$，根据以下算法进行求解：

其中算法2是一种基于改进的对称SOR迭代的内/外迭代方法，有关MSSOR方法的更多信息，请参见 [27] [28]，内外迭代法是数值线性代数中的一种基本策略，同样的思想也用于不精确的厄米/斜厄米分裂迭代 [29]。

对于任意 $\alpha \in \left(0,2\right)$，算法2生成的序列 $\left(z^{\left(k\right)},w^{\left(k\right)}\right)$ 收敛到 $\left(z^{*},w^{*}\right)$ 满足某些 ${\lambda }^{*}$， $\left\{z^{*},w^{*},{\lambda }^{*}\right\}$ 的条件(15)、(16)和(17)，此定理类似的详细证明见文献 [26]。

3. 实验结果

通过具体的数值实验，我们检验了所提出的算法(由Proposed表示)的有效性，其中恢复信号的质量是通过迭代步骤的数量(由Iter表示)、以秒为单位的消耗的中央处理器时间(由CPU表示)和原始信号的平均均方误差(MSE)来衡量。这里，MSE的定义为：

$\text{MSE}=\frac{1}{n}{\Vert \bar{z}-z^{*}\Vert }^2$

其中 $\bar{z}$ 是 $z^{*}$ 的估计值，显然平均均方误差反映了模型的稳健性。本文实验过程中所使用到的算法如表1所示：

Table 1. Abbreviations of detection methods

表1. 检测方法的缩写

3.1. 稀疏信号恢复

本文的第一个实验是通过解决噪声测试问题来检测算法效率的。其中原始信号 $\bar{z}$ 的长度为2048，随机生成64个非零元素，即它的稀疏级别是64，测量的个数为m = 512，其中包含高斯噪声(正态分布为N(0_m, σ²I_m)的随机向量，0_m为零向量，I_m是大小为m的单位矩阵)，我们的任务是从噪声测试中恢复z，其中图1中，原始稀疏信号为最上方的图、噪声测量是第二个图，不同算法的恢复信号如剩余图所示。图2中显示了三个算法的数值性能，其中包含Iter，CPU，MSE。与IPBDF，MSOR和ADMM算法的实验效果相比，本文提出的算法可以用更少的迭代次数和从原始信号中恢复出相同信号所需时间。从图可以看出，在大多数情况下，当算法恢复信号的质量相同时，本文所提出的方法在数值性能方面都优于IPBDF，MSOR和ADMM方法。

3.2. 模糊图像恢复

本文的第二个实验是通过恢复模糊图像来检测算法效率的，所有的测试问题都来自网站上的测试图像集合，分别由lake (P1)、columbia (P2)、bridge (P3)、crowd (P4)命名，其中columbia的尺寸为480 × 480，其他的尺寸为512 × 512。本文提出的算法在下图中由Proposed表示，在MSOR方法中，我们设 $\alpha =1.2$， $\Omega =\theta D$，实际计算中所用的迭代参数 $\theta$ 是通过实验中的最小化相应的迭代步骤得到的，在ADMM中，假设 $\Lambda =I$， $\rho ={10}^{-6}$，在我们提出的算法中，假设 $\Lambda =D$， $\rho ={10}^{-3}$。容易地看出，对于lake (P1)、columbia (P2)、bridge (P3)、crowd (P4)这四幅原始图像，本文提出的算法是重建图像质量较好的选择，实验结果见图3~6。

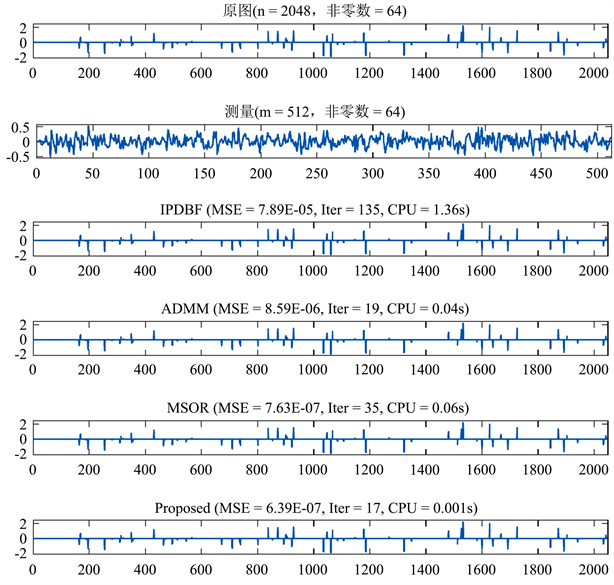
Figure 1. From top to bottom: IPBDF, MSOR and ADMM and the original signal, measured signal and recovered signal of the proposed algorithm

图1. 从上到下：IPBDF，MSOR和ADMM以及所提出算法的原始信号、测量信号和恢复信号

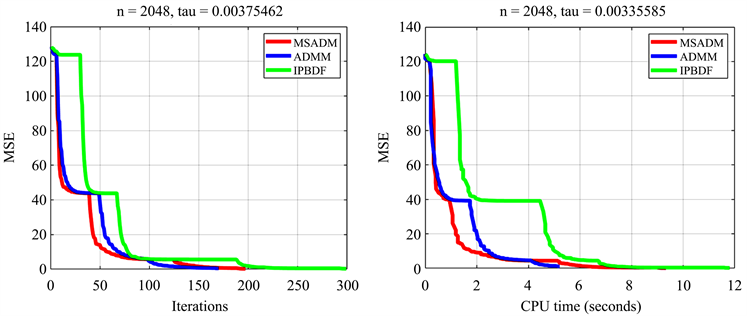
Figure 2. Comparison results of MSADM, ADMM, and IPBDF, the x-axis represents the number of iterations (top) and the CPU time in seconds (bottom), and the y-axis represents the MSE value

图2. MSADM、ADMM、IPBDF的比较结果，x轴表示迭代次数(上)以及以秒为单位的CPU时间(下)，y轴表示MSE值

Figure 3. Original lake image, blurred image and IPBDF, MSOR (top), ADMM, Proposed (bottom) restored image

图3. Lake原图，模糊图像和IPBDF，MSOR (顶部)，ADMM，Proposed (底部)恢复后的图像

Figure 4. Columbia original image, blurred image and IPBDF, MSOR (top), ADMM, Proposed (bottom) restored image

图4. Columbia原图，模糊图像和IPBDF，MSOR (顶部)，ADMM，Proposed (底部)恢复后的图像

Figure 5. Bridge original image, blurred image and IPBDF, MSOR (top), ADMM, Proposed (bottom) restored image

图5. Bridge原图，模糊图像和IPBDF，MSOR (顶部)，ADMM，Proposed (底部)恢复后的图像

Figure 6. Crowd original image, blurred image and IPBDF, MSOR (top), ADMM, Proposed (bottom) restored image

图6. Crowd原图，模糊图像和IPBDF，MSOR (顶部)，ADMM，Proposed (底部)恢复后的图像

4. 总结

本文将信号恢复问题放入优化问题的框架中，提出了一种基于MSSOR求解信号恢复问题的ADMM方法，与已有的结果相比，我们的贡献总结如下：

1) 本文首先将信号恢复问题重新表述为一个非线性非光滑问题，而不是直接用优化模型来描述。

2) 本文所使用的MSADM算法具有较强的鲁棒性，具有接近较优的收敛速度，特别适合于求解自适应精细网格进行离散化、高度非均匀、具有粗糙解的困难问题。

3) 通过与现有算法的数值效率相比较，本文解决了以往文献中存在的许多测试精度问题。数值结果表明，MSADM算法是一种鲁棒的稀疏信号恢复算法或模糊图像恢复算法。它既可以在更少的时间内恢复信号，也提升了图像质量，但是有关信号恢复的问题还可以做进一步的研究。

NOTES

^*第一作者。

^#通讯作者。