高振荡Bessel变换的新型Hermite卷积积分公式及其应用

Novel Hermite Convolution Quadrature for a Class of Highly Oscillatory Bessel Transforms and Its Application

摘要: 高振荡问题已广泛出现于许多科学工程应用领域，例如电磁、声波散射、量子化学和图像分析等问题。高振荡数值积分是高振荡问题数值解中的重要研究方向，由于其被积函数具有高振荡性，传统数值积分解法面临许多挑战。基于Lubich的卷积求积，本文针对一类高振荡的Bessel变换提出了一种新型的Hermite卷积积分公式，并研究了其在高振荡Volterra积分方程的数值解中的应用。通过理论与数值实验表明，该方法在计算含高振荡Bessel核的卷积积分以及积分方程时，计算精度不受振荡频率的影响，是一种高效的计算方法。

Abstract: Highly oscillatory problems frequently arise in many science and engineering fields, such as electromagnetic, acoustic scattering, quantum chemistry and image analysis problems. Numerical calculation of highly oscillatory integration is an important research interest of numerical studies on highly oscillatory problems. Due to the high oscillation of the integrand, classical numerical integration encounters great challenges. Based on Lubich’s convolution quadrature, this paper proposes novel Hermite convolution quadrature for a class of highly oscillatory Bessel transforms and studies its application in the numerical solutions to highly oscillatory Volterra integral equations. Both theoretical and numerical evidences indicate that the proposed method is particularly efficient in computing highly oscillatory integrals and solving highly oscillatory integral equations, and its accuracy is not affected by the oscillation parameter.

1. 引言

在很多应用领域，高振荡积分数值计算问题是一个非常重要的研究课题。在量子化学、图像分析、电动力学、正电子发射型断层扫描术、单光子发射型断层扫描术、流体力学等问题 [1] [2] [3] [4] [5] 的处理中，高振荡积分的高效计算往往是其研究的核心。一般地，振荡积分可以写成：

${\displaystyle {\int }_0^{b}f\left(t\right)g\left(t\right)\text{d}t}$，

这里 $f(\cdot )$ 表示高度振荡函数， $g(\cdot )$ 是缓慢变化的。

高振荡积分中的高振荡性质是导致数值计算极其困难的元凶，因为这使得传统的数值积分方法必须采用非常小的离散步长或是非常多的基底函数才能获得有意义的数值结果，然而这会导致其计算成本高昂到现有计算机系统无法承受的地步。鉴于此，高振荡积分的数值计算至今被认为是一项极具挑战性的数值难题。

过去几十年，高振荡积分计算的研究迅速发展 [6]。基于Filon的思想 [7]，Iserles和Nørsett [8] 通过其Hermite插值近似缓慢变化的函数来发展Filon类型的方法。理论和数值结果表明，该方法相对于频率具有高阶收敛速度。为了得到稳定和快速的算法，Domínguez [9] 和Xiang等人 [10] 分别提出了Clenshaw-Curtis-Filon型方法，Majidian等人分析了其稳定性 [11]，目前得到了广泛的应用。

虽然Filon的方法衍生出了许多有效的算法，但大多数算法都使矩积分的计算复杂化。解决这一问题的另一种方法是在复平面上改变积分路径，并推导出数值最速下降法 [12]。高振荡积分的另一个重要的求积规则是Levin法 [13]，它不计算复杂矩，从而得到广泛的应用。该方法的核心是将积分问题转化为常微分方程，并通过配置法求解该方程。在 [14] 中，Li提出了一种病态系统的SVD求解器。在 [15] 中，Suliman对带有紧支撑径向基函数的高振荡积分构造了一种条件良好且有效的Levin方法。

计算高振荡积分还有许多其他重要的方法，如同伦摄动法 [16]、广义求积规则 [17]、外推法 [18]，然而高振荡积分 [19] [20] [21] 的卷积积分公式被人关注较少，特别是它在高振荡情况下的渐近分析。事实上，卷积积分公式能够有效地计算卷积积分并且在解决振荡和进化问题中发挥着重要作用 [22]。因此，研究高振荡卷积积分的高效卷积求积公式具有重要意义。本文针对高振荡Bessel变换，提出改进的卷积求积公式，新公式在计算高振荡积分时不受振荡频率的影响。

2. 新型Hermite卷积积分公式的构造

考虑含高振荡Bessel核的卷积积分

${\displaystyle {\int }_0^x{J}_m\left(\omega t\right)g\left(x-t\right)\text{d}t},w\ge 1$， (1)

这里 $J_m(\cdot )$ 指m阶第一类Bessel函数，m为非负整数，并且 $J_m\left(\omega s\right)$ 的Laplace变换可以表示为

$F_{J_m}\left(s\right)=\frac{{\left(\sqrt{s^2+{\omega }^2}-s\right)}^m}{{\omega }^m\sqrt{s^2+{\omega }^2}}$。

则可以得到

$J_m\left(\omega t\right)=\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_{J_m}\left(\lambda \right){\text{e}}^{\lambda t}}\text{d}t$， (2)

这里的 $\Gamma$ 是 $F_{J_m}\left(s\right)$ 的解析区域内由 $\infty \cdot {\text{e}}^{-i\left(\pi -\phi \right)}$ 到 $\infty \cdot {\text{e}}^{i\left(\pi -\phi \right)}$ 的一条曲线，将式(2)代入式(1)可得：

${\displaystyle {\int }_0^x{J}_m\left(\omega t\right)g\left(x-t\right)\text{d}t}=\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_{J_m}\left(\lambda \right){\displaystyle {\int }_0^x{\text{e}}^{\lambda t}}}g\left(x-t\right)\text{d}t\text{d}\lambda$， (3)

注意到函数 ${\displaystyle {\int }_0^x{\text{e}}^{\lambda t}g\left(x-t\right)\text{d}t}$ 是初值问题

$\{\begin{array}{l}\frac{\text{d}y}{\text{d}x}=\lambda y\left(x\right)+g\left(x\right)\\ \frac{{\text{d}}^{2}y}{\text{d}{x}^2}=\lambda \frac{\text{d}y}{\text{d}x}+\frac{\text{d}g}{\text{d}x}\\ y\left(0\right)=0\\ y^{\prime }\left(0\right)=g\left(0\right)\end{array}$ (4)

的解。

设区间I由网格离散为 $I_h=\left\{t_n:=nh,n=0,\cdots ,N,h\ge 0,Nh=T\right\}$，令 $H\left(x\right)$ 是 $y\left(x\right)$ 在区间 $\left[t_n,t_{n+1}\right]$ 上的两点三次Hermite插值多项式，即

$\begin{array}{c}H\left(x\right)=\frac{2x-3t_n+t_{n+1}}{{\left(t_{n+1}-t_n\right)}^3}{\left(x-t_{n+1}\right)}^2{y}_n+\frac{-2x-t_n+3t_{n+1}}{{\left(t_{n+1}-t_n\right)}^3}{\left(x-t_n\right)}^2{y}_{n+1}\\ +\frac{{\left(x-t_{n+1}\right)}^2\left(x-t_n\right)}{{\left(t_{n+1}-t_n\right)}^2}{y^{\prime }}_n+\frac{\left(x-t_{n+1}\right){\left(x-t_n\right)}^2}{{\left(t_{n+1}-t_n\right)}^2}{y^{\prime }}_{n+1},\end{array}$ (5)

利用Hermite配置法求解上述初值问题可以近似地得到积分 ${\displaystyle {\int }_0^x{\text{e}}^{\lambda t}g\left(x-t\right)\text{d}t}$ 的值，即

$\left(\begin{array}{cc}0& 1\\ {\beta }_n& {\beta }_{n+1}\end{array}\right)\left(\begin{array}{l}{y}_{n+1}\\ {y^{\prime }}_{n+1}\end{array}\right)+\left(\begin{array}{cc}0& 1\\ {\alpha }_n& {\alpha }_{n+1}\end{array}\right)\left(\begin{array}{l}{y}_n\\ {y^{\prime }}_n\end{array}\right)=\lambda I\left(\begin{array}{l}{y}_{n+1}\\ {y^{\prime }}_{n+1}\end{array}\right)+I\left(\begin{array}{l}{g}_{n+1}\\ {g^{\prime }}_{n+1}\end{array}\right)$， (6)

这里 ${\beta }_n=-6h^{-2},{\beta }_{n+1}=4h^{-1},{\alpha }_n=6h^{-2},{\alpha }_{n+1}=2h^{-1}$。在式(6)中两边同时乘以 ${\zeta }^n\left(n\ge 0\right)$ 并做和可得

$\left(\begin{array}{cc}0& 1\\ {\beta }_n& {\beta }_{n+1}\end{array}\right)Y\left(\zeta \right)+\left(\begin{array}{cc}0& 1\\ {\alpha }_n& {\alpha }_{n+1}\end{array}\right)\zeta Y\left(\zeta \right)=\lambda IY\left(\zeta \right)+IG\left(\zeta \right)$， (7)

其中 $Y\left(\zeta \right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\left(\begin{array}{l}{y}_n\\ {y^{\prime }}_n\end{array}\right){\zeta }^n}$， $G\left(\zeta \right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\left(\begin{array}{l}{g}_n\\ {g^{\prime }}_n\end{array}\right){\zeta }^n}$，令

$\delta \left(\zeta \right)=h\left(\left(\begin{array}{cc}0& 1\\ {\beta }_n& {\beta }_{n+1}\end{array}\right)+\left(\begin{array}{cc}0& 1\\ {\alpha }_n& {\alpha }_{n+1}\end{array}\right)\zeta \right)$， (8)

可以得到

$Y\left(\zeta \right)={\left(\frac{\delta \left(\zeta \right)}{h}-\lambda \right)}^{-1}G\left(\zeta \right)$， (9)

从而由Cauchy积分公式可得

$\begin{array}{c}\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_{J_m}\left(\lambda \right)y\left(\zeta \right)\text{d}\lambda }=\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_{J_m}\left(\lambda \right)\left(\frac{\delta \left(\zeta \right)}{h}-\lambda \right)g\left(\zeta \right)\text{d}\lambda }\\ =F_{J_m}\left(\frac{\delta \left(\zeta \right)}{h}\right)g\left(\zeta \right),\end{array}$ (10)

这里 ${\zeta }^n$ 对应得系数矩阵的第一个元素即为积分(1)在 $x=nh$ 处的一个近似。设函数 $F_{J_m}\left(\frac{\delta \left(\zeta \right)}{h}\right)$ 在 $\zeta =0$ 处的一个Taylor展开为

$F_{J_m}\left(\frac{\delta \left(\zeta \right)}{h}\right)={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{W}_j\left(h\right){\zeta }^j}$， (11)

则计算积分(1)的新型Hermite卷积积分公式定义为

$Q_h^{HCQ}\left(x\right)={\left(1,0\right)}^{\text{T}}{\displaystyle \underset{0\le jh\le x}{\sum }{W}_j\left(h\right)G\left(x-jh\right)}$，(12)

由Taylor展开系数的定义，可得

$W_j\left(h\right)=\frac{1}{2\pi i}{\displaystyle {\int }_{\left|z\right|=\rho }{F}_{J_m}\left(\frac{\delta \left(\zeta \right)}{h}\right)z^{-n-1}\text{d}z}$， (13)

其中 $\rho$ 足够小使得圆盘 $\left|z\right|\le \rho$ 落在函数 $F_{J_m}\left(\frac{\delta \left(\zeta \right)}{h}\right)$ 的解析区域内。在上式中引入变量替换 $z=\rho {\text{e}}^{i\theta }$，我们可以得到

$W_j\left(h\right)=\frac{{\rho }^{-n}}{2\pi }{\displaystyle {\int }_0^{2\pi }{F}_{J_m}}\left(\frac{\delta \left(\rho {\text{e}}^{i\theta }\right)}{h}\right){\text{e}}^{-in\theta }\text{d}\theta$， (14)

利用梯形公式去离散这一积分就有

$\begin{array}{c}{\displaystyle {\int }_0^{2\pi }{F}_{J_m}\left(\frac{\delta \left(\rho {\text{e}}^{i\theta }\right)}{h}\right){\text{e}}^{-in\theta }\text{d}\theta }={\displaystyle \underset{l=0}{\overset{L-1}{\sum }}{\displaystyle {\int }_{l\frac{2\pi }{L}}^{\left(l+1\right)\frac{2\pi }{L}}{F}_{J_m}\left(\frac{\delta \left(\rho {\text{e}}^{i\theta }\right)}{h}\right){\text{e}}^{-in\theta }\text{d}\theta }}\\ \approx {\displaystyle \underset{l=0}{\overset{L-1}{\sum }}\frac{\pi }{L}}\left(F_{J_m}\left(\frac{\delta \left(\rho {\text{e}}^{il\frac{2\pi }{L}}\right)}{h}\right){\text{e}}^{-inl\frac{2\pi }{L}}+F_{J_m}\left(\frac{\delta \left(\rho {\text{e}}^{i\left(l+1\right)\frac{2\pi }{L}}\right)}{h}\right){\text{e}}^{-in\left(l+1\right)\frac{2\pi }{L}}\right)\\ =\frac{2\pi }{L}{\displaystyle \underset{l=0}{\overset{L-1}{\sum }}{F}_{J_m}\left(\frac{\delta \left(\rho {\text{e}}^{il\frac{2\pi }{L}}\right)}{h}\right){\text{e}}^{-inl\frac{2\pi }{L}}},\end{array}$ (15)

这里为了保证 $\sqrt{\epsilon }$ 的计算精度，我们选取 $L=10N$， ${\rho }^n=\sqrt{\epsilon }$，而积分权(13)可以通过快速Fourier变换计算，计算量为 $O\left(N\log N\right)$。

3. 依振荡频率的收敛性分析

由于卷积积分公式的离散形式与振荡频率 $\omega$ 无关，可以预测这种方法在计算高振荡积分的时候不会随着频率的增大而损失计算精度。为了进一步研究这一类公式在计算高振荡积分时的可靠性，我们首先介绍一个引理。

引理1. [23] 假设函数 $g(\cdot )$ 在区间I上连续，这里I是正半轴上的有限闭区间或者 $\left[a,\infty \right)$， $a\ge 0$ 且积分 ${\displaystyle {\int }_S\left|g\left(t\right)\right|\text{d}t},{\displaystyle {\int }_S\left|g^{\prime }\left(t\right)\right|\text{d}t}$ 存在。那么对于任意的正数 $v\ge 0$，当 $\omega$ 趋向于无穷大时，存在与 $\omega$ 无关的常数C使得

$\left|{\displaystyle {\int }_{S}g}\left(t\right)J_m\left(\omega t\right)\text{d}t\right|\le C{\omega }^{-1}$，

进一步，如果积分区间S不包含零点，那么有

$\left|{\displaystyle {\int }_{S}g}\left(t\right)J_m\left(\omega t\right)\text{d}t\right|\le C{\omega }^{-3/2}$。

下面考虑Hermite卷积积分公式计算高振荡积分时的一些性质。

定理1. 在积分(16)中，若函数 $g(\cdot )$ 在正半轴上二次连续可微，且积分 ${\displaystyle {\int }_0^b\left|g\left(t\right)\right|\text{d}t}$， ${\displaystyle {\int }_0^b\left|g^{\prime }\left(t\right)\right|\text{d}t}$， ${\displaystyle {\int }_0^b\left|g^{″}\left(t\right)\right|\text{d}t}$ 存在。那么当 $\omega$ 趋向于无穷大时，存在常数 $C>0$，使得Hermite卷积积分公式的误差满足

$\left|Q_h^{HCQ}\left(b\right)-I\left[g\right]\right|\le C{\omega }^{-3/2}$。

证明：令 ${\delta }_j$ 为 $\delta \left(\zeta \right)={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\delta }_j}{\zeta }^j$ 的 ${\zeta }^j$ 的系数，并且定义

$s_{h}G\left(x\right):=\frac{1}{h}{\displaystyle \underset{0\le jh\le x}{\sum }{\delta }_j}G\left(x-jh\right),0<x\le b$， (16)

这里 $G\left(x\right)=\left(\begin{array}{c}g\left(x\right)\\ g^{\prime }\left(x\right)\end{array}\right)$。

令 $b={\left(1,0\right)}^{\text{T}}$，由卷积积分公式的定义，其可以表示成Dunford-Taylor积分的形式

$\mathcal{F}\left(s_h\right)g\left(x\right)=\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_{J_m}}\left(\lambda \right)b^{\text{T}}{\left(s_h-\lambda \right)}^{-1}G\left(x\right)\text{d}\lambda$， (17)

又因为

$F_{J_m}\left(s\right)={\displaystyle {\int }_0^{\infty }{\text{e}}^{-ts}}{J}_m\left(\omega t\right)\text{d}t$， (18)

将上式代入等式(17)得

$\begin{array}{c}\mathcal{F}\left(s_h\right)g\left(x\right)=\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{\displaystyle {\int }_0^{\infty }{\text{e}}^{-t\lambda }}}{J}_m\left(\omega t\right)b^{\text{T}}{\left(s_h-\lambda \right)}^{-1}G\left(x\right)\text{d}t\text{d}\lambda \\ ={\displaystyle {\int }_0^{\infty }{J}_m}\left(\omega t\right)b^{\text{T}}{\text{e}}^{-t{s}_h}G\left(x\right)\text{d}t,\end{array}$ (19)

将 $I\left[g\right]$ 表示成如下形式

$\mathcal{F}\left(s\right)g\left(x\right)={\displaystyle {\int }_0^x{J}_m}\left(\omega t\right)g\left(x-t\right)\text{d}t={\displaystyle {\int }_0^x{J}_m}\left(\omega t\right)b^{\text{T}}G\left(x-t\right)\text{d}t$， (20)

因此

$\begin{array}{l}\mathcal{F}\left(s_h\right)g\left(x\right)-\mathcal{F}\left(s\right)g\left(x\right)\\ ={\displaystyle {\int }_0^x{J}_m}\left(\omega t\right)\left(b^{\text{T}}{\text{e}}^{-t{s}_h}G\left(x\right)-b^{\text{T}}G\left(x-t\right)\right)\text{d}t+{\displaystyle {\int }_x^{\infty }{J}_m}\left(\omega t\right)b^{\text{T}}{\text{e}}^{-t{s}_h}G\left(x\right)\text{d}t.\end{array}$ (21)

定义 ${\varphi }_1\left(t\right):=b^{\text{T}}{\text{e}}^{-t{s}_h}G\left(x\right)-b^{\text{T}}G\left(x-t\right)$ 和 ${\varphi }_2\left(t\right):=b^{\text{T}}{\text{e}}^{-t{s}_h}G\left(x\right)$，由Bessel函数的求导性质可得

$\begin{array}{c}\mathcal{F}\left(s_h\right)g\left(x\right)-\mathcal{F}\left(s\right)g\left(x\right)={\displaystyle {\int }_0^x{J}_m}\left(\omega t\right){\varphi }_1\left(t\right)\text{d}t+{\displaystyle {\int }_x^{\infty }{J}_m}\left(\omega t\right){\varphi }_2\left(t\right)\text{d}t\\ ={\varphi }_1\left(0\right){\displaystyle {\int }_0^x{J}_m}\left(\omega t\right)\text{d}t+\frac{1}{\omega }\left({\varphi }_1\left(t\right)-{\varphi }_1\left(0\right)\right){J_{m+1}\left(\omega t\right)|}_{t=0}^x\\ -\frac{1}{\omega }{\displaystyle {\int }_0^x\left({{\varphi }^{\prime }}_1\left(t\right)-\frac{m+1}{t}\left({\varphi }_1\left(t\right)-{\varphi }_1\left(0\right)\right)\right)J_{m+1}\left(\omega t\right)\text{d}t}\\ +\frac{1}{\omega }{\varphi }_2\left(t\right){J_{m+1}\left(\omega t\right)|}_{t=x}^{\infty }-\frac{1}{\omega }{\displaystyle {\int }_x^{\infty }\left({{\varphi }^{\prime }}_2\left(t\right)-\frac{m+1}{t}{\varphi }_2\left(t\right)\right)J_{m+1}\left(\omega t\right)\text{d}t},\end{array}$ (22)

由 ${\varphi }_1\left(0\right)=0$ 和引理1可得，存在常数 $C>0$ 使得

$\left|\mathcal{F}\left(s_h\right)f\left(x\right)-\mathcal{F}\left(s\right)f\left(x\right)\right|\le C{\omega }^{-3/2}$，

证毕。

4. 数值实验

在本节中，我们通过几个数值算例来诠释上文提出的Hermite卷积积分公式在计算高振荡积分时的高效性。

例1. 我们考虑以下两个高振荡积分

$I_1={\displaystyle {\int }_0^2{J}_0\left(\omega \left(2-t\right)\right)\frac{1}{1+25t^2}\text{d}t}$， $I_2={\displaystyle {\int }_0^1{J}_1\left(\omega \left(1-t\right)\right)\cos \left(t\right){\text{e}}^{-t}\text{d}t}$ (23)

在表1中，我们可以看到这种方法计算上述积分得到的关于不同频率 $\omega$ 的绝对误差。在图1和图2中，我们展示了Hermite卷积求积公式计算此类高振荡积分的收敛速度。数值结果表明，Hermite卷积积分公式在计算此类高振荡积分方面具有较好效果，其关于频率 $\omega$ 渐近阶能够达到 $O\left({\omega }^{-3/2}\right)$。可以看出，这些计算结果与之前的定理中给出的渐近阶的估计是吻合的。

Table 1. The absolute errors of the numerical solution obtained by using the Hermite Convolution Quadtrature to solve integral (23)

表1. 利用Hermite卷积积分公式求(23)所得数值解的绝对误差

5. 在高振荡Volterra积分方程数值解中的应用

5.1. Hermite卷积积分公式求解高振荡Volterra积分方程

在物理学、工程等领域的诸多问题最终都可以转化为第一类卷积型Volterra积分方程的求解。例如，对于二维声学散射问题中的单层势能积分方程

$\frac{1}{2\pi }{\displaystyle {\int }_{R^2}\frac{u\left(x^{\prime },t-\left|x^{\prime }-x\right|\right)}{\left|x^{\prime }-x\right|}\text{d}{x}^{\prime }}=a\left(x,t\right),\left(x,t\right)\in R^2\times \left(0,T\right)$

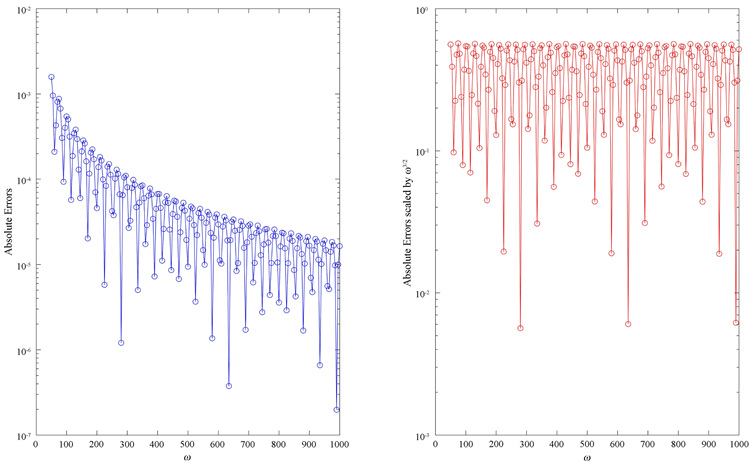
Figure 1. Absolute errors of $I_1$ (left) and its transformation law with respect to $\omega$ (right)

图1. $I_1$ 的绝对误差(左)与绝对误差关于 $\omega$ 的变换规律(右)

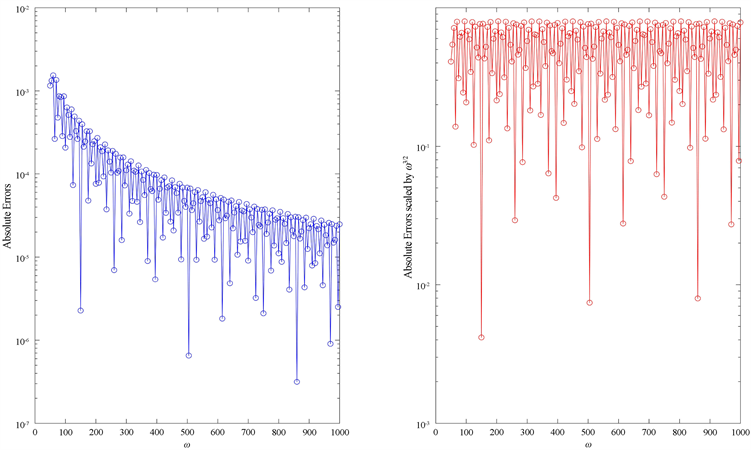
Figure 2. Absolute errors of $I_2$ (left) and its transformation law with respect to $\omega$ (right)

图2. $I_2$ 的绝对误差(左)与绝对误差关于 $\omega$ 的变换规律(右)

当 $t\le 0$，满足 $u\equiv 0$， $a\equiv 0$ 时，上式可以利用连续Fourier变换转化为带Bessel核的第一类卷积型Volterra积分方程：

${\displaystyle {\int }_0^x{J}_0\left(\omega \left(x-t\right)\right)u\left(t\right)\text{d}t}=g\left(x\right),x\in \left[0,T\right]$， (24)

这里 $g(\cdot )$ 足够光滑且 $g\left(0\right)=0$。

此时 $I_h=\left\{t_n:=nh,n=0,\cdots ,N,h\ge 0,Nh=T\right\}$ 是 $\left[0,T\right]$ 上的等距网格，且 $h=\frac{T}{N}$。对此方程应用Hermite卷积积分公式，可以得到

${\left(1,0\right)}^{\text{T}}{\displaystyle \underset{j=0}{\overset{k}{\sum }}{W}_{k-j}\left(\begin{array}{l}{u}_j\\ {u^{\prime }}_j\end{array}\right)}=g_k$。 (25)

对(24)求导可得

${\displaystyle {\int }_0^x\omega {J^{\prime }}_0\left(\omega \left(x-t\right)\right)u\left(t\right)\text{d}t}+u\left(x\right)=g^{\prime }\left(x\right)$， (26)

对此方程应用Hermite卷积积分公式，可以得到

${\left(1,0\right)}^{\text{T}}{\displaystyle \underset{j=0}{\overset{k}{\sum }}{W^{\prime }}_{k-j}\left(\begin{array}{l}{u}_j\\ {u^{\prime }}_j\end{array}\right)}+u_k={g^{\prime }}_k$。 (27)

这里的W和 $W^{\prime }$ 是Hermite卷积积分对应的权矩阵， $u_j$， ${u^{\prime }}_j$ 分别表示 $u\left(x\right)$ 和 $u^{\prime }\left(x\right)$ 在 $t_j$ 处的数值解， $g_j$， ${g^{\prime }}_j$ 分别表示 $g\left(x\right)$ 和 $g^{\prime }\left(x\right)$ 在 $t_j$ 处的值。联立(25)和(27)得到一个线性系统，对此线性系统求解即可得到均匀网格 $I_h$ 处的数值解。

5.2. 数值实验

卷积求积公式是求解具有卷积核的Volterra方程的重要工具。许多数值实验表明，它们对于求解一些高振荡的Volterra积分方程是有效的。

例2. 考虑以下高振荡Volterra积分方程

${\displaystyle {\int }_0^x{J}_0\left(\omega \left(x-t\right)\right)u\left(t\right)\text{d}t}=x{\text{e}}^{-x}$。 (28)

在这个例子中，我们考虑了Hermite卷积积分公式在求解高振荡Volterra积分方程中的应用。首先，通过让 $T=2$ 和 $N=4$，我们在表2和图3中给出了此方法关于不同频率 $\omega$ 的绝对误差。这些表和图中列出的绝对误差表明，此方法具有振荡频率越高，近似值就越好的性质。

Table 2. The absolute errors of the numerical solution obtained by using the Hermite convolution quadtrature to solve Equation (28)

表2. 利用Hermite卷积积分公式求解方程(28)所得数值解的绝对误差

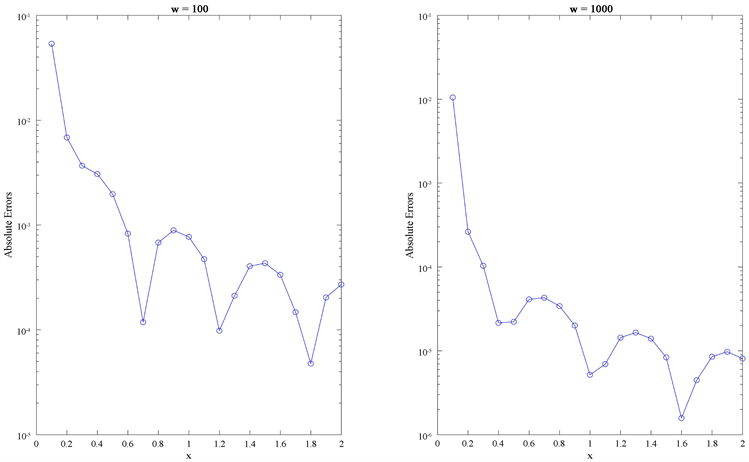
Figure 3. The absolute errors of the numerical solution obtained by using the Hermite convolution quadtrature to solve equation (28) ( $\omega =100,1000$ )

图3. Hermite卷积积分公式求解(28)所得数值解的绝对误差( $\omega =100,1000$ )

6. 总结

本文提出了高振荡Bessel变换的新型Hermite卷积积分公式，研究了此公式在处理高振荡积分数值计算问题时的一些性质。第2节的理论结果揭示了该公式相对于频率 $\omega$ 的收敛速度，当 $\omega$ 趋于无穷大时，Hermite卷积积分公式以频率 $\omega$ 的负幂收敛，即 $O\left({\omega }^{-3/2}\right)$。在第3节中，我们通过两个数值算例验证了第2节中理论的准确性。在第4节我们应用Hermite卷积积分公式求解带高振荡Bessel核的Volterra卷积积分方程，通过数值实验表明，此类方法是有效的。此外，本文仅仅为高振荡积分数值计算问题的新型Hermite求积公式收敛理论打开了一扇窗，未来需要对此方法进行改进，从而得到更高的收敛阶。

参考文献

NOTES

^*通讯作者。