具有双约束条件的变分不等式的二阶微分方程方法

The Second-Order Differential Equation Method for Variational Inequality with Cou-pling Constraints

摘要: 本文研究的主要内容是具有双约束条件的变分不等式问题。将具有双约束条件的变分不等式看作一类特殊的优化问题，运用该优化问题的拉格朗日函数的鞍点不等式和投影算子，建立了具有控制过程的二阶微分方程系统，并证明了该微分方程系统的解的轨迹的聚点是具有双约束条件的变分不等式的解。最后，运用具有控制过程的二阶微分方程系统求解了两个算例，该数值结果验证了该方法的有效性。

Abstract: In this paper, we consider the second-order differential equation method for solving the variational inequality with coupling constraints. The variational inequality with coupling constraints is regarded as a special optimization problem. Using the saddle point inequality and projection op-erator of Lagrange function, the second-order differential equation system with control process is established, and it is proved that the convergence point of the solution trajectory of this differential equation system is the solution of the variational inequality with coupling constraints. Finally, two numerical examples are solved by using the second-order differential equation system with control process, and the numerical results verify the effectiveness of this method.

1. 引言

本文将研究具有双约束条件的变分不等式问题：求解 $v^{\ast }\in \Omega$ 使得到

$\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle \ge 0,\forall w\in \Omega ,g\left(v^{\ast },w\right)\le 0,$ (1.1)

其中 $F\left(v\right):{\Re }^n\to {\Re }^n,g\left(v^{\ast },w\right):{\Re }^n\times {\Re }^n\to {\Re }^m$ 是两个映射， $\Omega \subset {\Re }^n$ 是一个非空闭凸集合。

具有双约束条件的变分不等式问题出现在许多数学领域中，如下面的双人博弈问题：双约束的双人博弈问题(1.2)中可以转化为具有双约束条件的变分不等式问题(1.1)

$\begin{array}{l}{x}_1^{\ast }\in \text{Arg}\min \left\{f_1\left(x_1,x_2^{\ast }\right)|g_1\left(x_1,x_2^{\ast }\right)\le g_1\left(x_1^{\ast },x_2^{\ast }\right),v_1\in Q_1\right\},\\ x_2^{\ast }\in \text{Arg}\min \left\{f_2\left(x_1^{\ast },x_2\right)|g_1\left(x_1^{\ast },x_2\right)\le g_1\left(x_1^{\ast },x_2^{\ast }\right),v_2\in Q_2\right\},\end{array}$ (1.2)

其中 $f_1,f_2,g_1,g_2$ 都为 ${\Re }^n\times {\Re }^n\to {\Re }^1$ 上的映射。其中 $f_1$ 和 $g_1$ 对任意的 $v_2$ 在 $v_1$ 处是凸的，其中 $f_2$ 和 $g_2$ 对任意的 $v_1$ 在 $v_2$ 处是凸的。通过标准化函数

$\Phi \left(v,w\right)=f_1\left(x_1,y_2\right)+f_2\left(y_1,x_2\right),G\left(v,w\right)=g_1\left(x_1,y_2\right)+g_2\left(y_1,x_2\right)$ (1.3)

其中 $v=\left(y_1,y_2\right)$， $w=\left(x_1,x_2\right)$ 且 $v,w\in {\Omega }_0=Q_1\times Q_2$。通过标准化函数问题(1.2)可以转化为如下形式。

求解 $v^{\ast }\in {\Omega }_0$ 使得

$v^{\ast }\in \text{Argmin}\left\{\Phi \left(v^{\ast },w\right)|G\left(v^{\ast },w\right)-G\left(v^{\ast },v^{\ast }\right)\le 0,w\in {\Omega }_0\right\}.$ (1.4)

如果问题(1.4)和目标函数是可微的，那么它就可以表示成为一个变分不等式问题

$\langle {\nabla }_w\Phi \left(v^{\ast },v^{\ast }\right),w-v^{\ast }\rangle \ge 0,\forall w\in \Omega ,G\left(v^{\ast },w\right)\le G\left(v^{\ast },v^{\ast }\right),$ (1.5)

其中 ${\nabla }_w\Phi \left(v,v\right)={{\nabla }_w\Phi \left(v,w\right)|}_{v=w}$。

具有双约束条件的变分不等式问题还出现在许多其他的数学领域中，如：价值均衡问题的最简模型、拟变分不等式问题以及双层规划问题等。具体可参见Antipin [1]。

有限维变分不等式和互补问题的理论研究和算法研究被Facchinei和Pang [2] 进行了详细的总结和介绍，该专著被认为是优化界最有价值的著作，其内容记录了在 ${\Re }^n$ 空间中的研究变分不等式问题和互补问题的绝大部分重要成果，包括互补问题和变分不等式的稳定性分析、灵敏度分析、数值解法等。但是这本专著中没有记录变分不等式的微分方程方法。

近几年关于求解变分不等式的算法简单介绍如下：Nazemi和Sabeghi [3] [4] 应用神经网络模型有效的求解了凸二阶锥约束变分不等式问题。王莉，单峰和王诗云 [5] 通过运用增广拉格朗日法和非精确半光滑牛顿法求解了具有约束条件的变分不等式的一类子问题。米特特和方长杰 [6] 提出了一种惯性次梯度外梯度方法求解变分不等式问题。Kwelegano，Zegeye和Boikanyo [7] 研究了一种求解分裂等式变分不等式问题的近似解法。更多求解变分不等式的方法参阅文献 [8] - [13]。

在Antipin [1] 中提出了一个具有双约束条件的变分不等式。并将原变分不等式问题在一定条件下转换成鞍点问题。通过应用投影算子，建立一个微分方程系统，即微分方程系统解的聚点就是原问题的解。应用对称函数的性质，证明了微分方程解的轨迹的收敛性。但是，Antipin [1] 并没有给出具体算例说明本方法的可行性。Antipin [1] 通过建立的一阶微分方程系统来求解双约束变分不等式问题。本文将在此基础上，建立二阶的分方程系统来求解双约束变分不等式问题。

本文运用微分方程方法求解双约束变分不等式，与传统的微分方程方法或神经网络方法不同的是，我们直接从投影算子方程组建立微分方程系统，并且不必构造Lyapunov函数得到微分方程系统的解的轨迹的聚点是所研究的变分不等式问题的解。

本文内容如下：在第二节中会介绍对称函数的定义及其相关性质，这些性质在收敛定理的证明过程中会起到重要的作用；会将具有双约束条件的变分不等式问题看作一个特殊的优化问题，运用该优化问题的拉格朗日函数的鞍点不等式和投影算子得到具有双约束条件的变分不等式(1.1)的一系列等价表示；第三节，运用第二节得到的等价的投影算子方程建立具有控制过程的二阶微分方程系统，并运用对称函数的性质证明了该二阶微分方程系统的解的轨迹的收敛性；最后，运用具有控制过程的二阶微分方程系统求解了两个算例，说明了该方法的有效性。

2. 预备知识

下面对对称函数的定义和相关性质做如下介绍。

引理2.1 [14]：设H为Hilbert空间，且 $C\subset H$ 是一个闭凸集合。对于给定的 $z\in H,u\in C$ 满足

$\langle u-z,v-u\rangle \ge 0,\forall v\in C,$

当且仅当 $u-{\Pi }_C\left(z\right)=0$。

定义2.1 [1]： $g\left(v,w\right):{\Re }^n\times {\Re }^n\to {\Re }^m$ 称为是对称函数，如果满足下面的关系

$g\left(v,w\right)=g\left(w,v\right)\text{,}\forall w\in \Omega ,\forall v\in \Omega .$ (2.1)

与此同时，Antipin [1] 也给出了对称函数 $g\left(v,w\right)$ 的下面重要性质。

性质2.1 [1]：对称函数 $g\left(v,w\right):{\Re }^n\times {\Re }^n\to {\Re }^m$ 在集合 $\Omega \times \Omega$ 上关于第一元v和第二元w的梯度矩阵是相等的，即

${\nabla }_w^{\text{T}}g\left(v,v\right)={\nabla }_v^{\text{T}}g\left(v,v\right)\text{,}\forall v\in \Omega .$ (2.2)

证明：在(2.1)中左边关于第二元w和右边关于第一元v求导得

${\nabla }_w^{\text{T}}g\left(v,w\right)={\nabla }_v^{\text{T}}g\left(w,v\right)\text{,}\forall v\in \Omega ,\forall w\in \Omega ,$

其中 ${\nabla }_w^{\text{T}}g\left(v,w\right)$ 和 ${\nabla }_v^{\text{T}}g\left(w,v\right)$ 是 $m\times n$ 矩阵，在上式中令 $w=v$ 便得到(2.2)。证毕。□

性质2.2 [1]：对称函数 ${g\left(v,w\right)|}_{{}_{v=w}}$ 在集合 $\Omega \times \Omega$ 上梯度 ${\nabla }^{\text{T}}g\left(v,v\right)$ 与 ${2{\nabla }_w^{\text{T}}g\left(v,w\right)|}_{v=w}$ 是相等的，即

${2{\nabla }_w^{\text{T}}g\left(v,w\right)|}_{v=w}={\nabla }^{\text{T}}g\left(v,v\right)\text{,}\forall v\in \Omega .$ (2.3)

证明：根据可微的定义有

$g\left(v+h,w+k\right)=g\left(v,w\right)+{\nabla }_v^{\text{T}}g\left(v,w\right)h+{\nabla }_w^{\text{T}}g\left(v,w\right)k+o\left(v,w,h,k\right),$ (2.4)

其中 $o\left(v,w,h,k\right)/\sqrt{{\left|h\right|}^2+{\left|k\right|}^2}\to 0$，当 $\sqrt{{\left|h\right|}^2+{\left|k\right|}^2}\to 0$。

在(2.1)中令 $w=v,h=k$，则再由(2.2)和(2.3)可得

$g\left(v+h,v+h\right)=g\left(v,v\right)+2{\nabla }_w^{\text{T}}g\left(v,v\right)h+o\left(v,h\right),$ (2.5)

其中 $o\left(v,h\right)/\left|h\right|\to 0$，当 $\left|h\right|\to 0$。则(2.5)是(2.4)的特殊情形，由(2.5)可以知道 $g\left(v,v\right)$ 可以看作是函数 $g\left(v,w\right)$ 当 $v=w$ 时的函数，其梯度为 ${\nabla }^{\text{T}}g\left(v,v\right)$，从(2.5)可以得到(2.3)成立。证毕。□

问题(1.1)可以看作是求解下面的优化问题

$\begin{array}{l}\min f\left(w\right),\\ \text{s}\text{.t}\text{.}g\left(v^{\ast },w\right)\le 0,\\ w\in \Omega ,\end{array}$ (2.6)

其中 $f\left(w\right)=\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle$，且由(1.1)是一类变分不等式可知 $f\left(w\right)\ge 0$，进一步 $v^{*}$ 是上述优化问题(2.6)的解。

可以得到，优化问题(2.6)的拉格朗日函数

$\mathcal{L}\left(v^{\ast },w,p\right)=\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle +\langle p,g\left(v^{\ast },w\right)\rangle ,\forall w\in \Omega ,\forall p\in {\Re }_{+}^m,$ (2.7)

其中 $v^{\ast }$ 是原问题的解，w和p分别是原始变量和对偶变量。由于 $v^{\ast }$ 是 $f\left(w\right)$ 在集合 $\Omega$ 上的最小值点，因此在一定正则条件下，点 $\left(v^{\ast },p^{\ast }\right)$ 为拉格朗日函数 $\mathcal{L}\left(v^{\ast },w,p\right)$ 的鞍点，即满足下面的鞍点不等式

$\begin{array}{c}\langle F\left(v^{\ast }\right),v^{\ast }-v^{\ast }\rangle +\langle p,g\left(v^{\ast },v^{\ast }\right)\rangle \le \langle F\left(v^{\ast }\right),v^{\ast }-v^{\ast }\rangle +\langle p^{\ast },g\left(v^{\ast },v^{\ast }\right)\rangle \\ \le \langle F\left(v^{\ast }\right),w-v^{\ast }\rangle +\langle p^{\ast },g\left(v^{\ast },w\right)\rangle ,\end{array}$ (2.8)

$\forall w\in \Omega ,\forall p\in {\Re }_{+}^m.$

鞍点不等式(2.8)可以等价地表示为

$\begin{array}{l}{v}^{\ast }\in \text{Argmin}\left\{\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle +\langle p^{\ast },g\left(v^{\ast },w\right)\rangle |w\in \Omega \right\},\\ p^{\ast }\in \text{Argmax}\left\{\langle p,g\left(v^{\ast },v^{\ast }\right)\rangle |p\in {\Re }_{+}^m\right\}.\end{array}$ (2.9)

如果函数 $g\left(v,w\right)$ 关于第二元w是可微的，即 ${\nabla }_{w}g\left(v,w\right)$ 存在，根据(2.8)和(2.9)可以得到下面的变分不等式组

$\begin{array}{l}\langle F\left(v^{\ast }\right)+{\nabla }_{w}g\left(v^{\ast },v^{\ast }\right)p^{\ast },w-v^{\ast }\rangle \ge 0,\forall w\in \Omega ,\\ \langle -g\left(v^{\ast },v^{\ast }\right),p-p^{\ast }\rangle \ge 0,\forall p\in {\Re }_{+}^m,\end{array}$ (2.10)

根据投影算子的定义及引理2.1，将变分不等式组(2.10)可表示为投影算子方程组

$\begin{array}{l}{v}^{\ast }={\Pi }_{\Omega }\left(v^{\ast }-\alpha \left(F\left(v^{\ast }\right)+{\nabla }_{w}g\left(v^{\ast },v^{\ast }\right)p^{\ast }\right)\right),\\ p^{\ast }={\Pi }_{+}\left(p^{\ast }+\alpha g\left(v^{\ast },v^{\ast }\right)\right),\end{array}$ (2.11)

其中 ${\Pi }_{\Omega }$ 和 ${\Pi }_{+}$ 为到集合 $\Omega$ 和正卦限 ${\Re }_{+}^m$ 上的投影， $\alpha >0$ 是参数。

下面对变分不等式组(2.10)进行计算，对(2.10)的第一个不等式展开

$\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle +\langle p^{\ast },{\nabla }_w^{T}g\left(v^{\ast },v^{\ast }\right)\left(w-v^{\ast }\right)\rangle \ge \text{0,}\forall w\in \Omega .$ (2.12)

如果 ${g\left(v,w\right)|}_{v=w}$ 是凸的和可微的，运用性质2.2中的(2.3)，(2.12)的第二项可以写成

$\begin{array}{c}\langle p^{\ast },{\nabla }_w^{\text{T}}g\left(v^{\ast },v^{\ast }\right)\left(w-v^{\ast }\right)\rangle =\frac{1}{2}\langle p^{\ast },{\nabla }^{\text{T}}g\left(v^{\ast },v^{\ast }\right)\left(w-v^{\ast }\right)\rangle \\ \le \frac{1}{2}\langle p^{\ast },g\left(w,w\right)-g\left(v^{\ast },v^{\ast }\right)\rangle .\end{array}$ (2.13)

由(2.13)式代入到(2.10)得到新的变分不等式组

$\begin{array}{l}\langle F\left(v^{\ast }\right),w-v^{\ast }\rangle +\frac{1}{2}\langle p^{\ast },g\left(w,w\right)-g\left(v^{\ast },v^{\ast }\right)\rangle \ge 0,\forall w\in \Omega ,\\ \langle -g\left(v^{\ast },v^{\ast }\right),p-p^{\ast }\rangle \ge 0,\forall p\in {\Re }_{+}^m.\end{array}$ (2.14)

注2.1：经过上述讨论，可以得到当 $g\left(v,w\right):{\Re }^n\times {\Re }^n\to {\Re }^m$ 是对称函数，且 $g\left(v,w\right)$ 关于第二元w是可微的，进一步如果 ${g\left(v,w\right)|}_{v=w}$ 是凸的和可微的，则(2.8)-(2.14)表达式彼此相互等价。

3. 二阶微分方程方法

在Antipin [1] 工作的基础上，通过投影算子方程组(2.11)建立具有控制过程的二阶微分方程系统如下

$\begin{array}{l}{\mu }_1\frac{{\text{d}}^{2}v}{\text{d}{t}^2}+{\beta }_1\frac{\text{d}v}{\text{d}t}+v={\Pi }_{\Omega }\left(v-\alpha \left(F\left(\bar{v}\right)+{\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p}\right)\right),v\left(t_0\right)=v_0,\stackrel{\dot{}}{v}\left(t_0\right)={\stackrel{\dot{}}{v}}_0,\\ {\mu }_2\frac{{\text{d}}^{2}p}{\text{d}{t}^2}+{\beta }_2\frac{\text{d}p}{\text{d}t}+p={\Pi }_{+}\left(p+\alpha g\left(\bar{v},\bar{v}\right)\right),p\left(t_0\right)=p_0,\stackrel{\dot{}}{p}\left(t_0\right)={\stackrel{\dot{}}{p}}_0,\end{array}$ (3.1)

其中

$\begin{array}{l}\bar{v}={\Pi }_{\Omega }\left(v-\alpha \left(F\left(v\right)+{\nabla }_{w}g\left(v,v\right)\bar{p}\right)\right),\\ \bar{p}={\Pi }_{+}\left(p+\alpha g\left(v,v\right)\right),\end{array}$ (3.2)

为控制过程，可以提高二阶微分方程系统轨迹的收敛速度，其中 ${\mu }_{\text{1}}>0,{\beta }_1>0,{\mu }_2>0,{\beta }_2>0$ 且 $\alpha >0$ 均是参数。如果 ${\mu }_1={\mu }_2=0$ 且 ${\beta }_1={\beta }_2=1$，这时系统(4.19)可退化为Antipin [1] 中的具有控制过程的一阶微分方程系统(6.2)，因此具有控制过程的二阶微分方程系统(3.1)和(3.2)是对Antipin [1] 中的一阶微分方程系统(6.2)的推广。以下为了书写方便，记 $\ddot{v}=\frac{{\text{d}}^{2}v}{\text{d}{t}^2},\ddot{p}=\frac{{\text{d}}^{2}p}{\text{d}{t}^2},\stackrel{\dot{}}{v}=\frac{\text{d}v}{\text{d}t},\stackrel{\dot{}}{p}=\frac{\text{d}p}{\text{d}t}$。

假设函数 ${g\left(v,w\right)|}_{v=w}$,F和 ${{\nabla }_w^{\text{T}}g\left(v,w\right)|}_{v=w}$ 都是Lipschitz连续的，其Lipschitz常数分别为 $\left|g\right|$， $\left|F\right|$ 和 $|\nabla |$。若当 $t\to \infty$ 时， $\left|\bar{p}\right|$ 有界，即存在 $C_0>0$ 使得 $\Vert \bar{p}\Vert \le C_0$。则根据上述条件及投影算子的非扩张性和微分方程系统(3.1)和(3.2)，得到下面的不等式

$\begin{array}{c}\Vert {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}+p-\bar{p}\Vert =\Vert {\Pi }_{+}\left(p+\alpha g\left(\bar{v},\bar{v}\right)\right)-{\Pi }_{+}\left(p+\alpha g\left(v,v\right)\right)\Vert \\ \le \alpha \Vert g\left(\bar{v},\bar{v}\right)-g\left(v,v\right)\Vert \\ \le \alpha \left|g\right|\Vert \bar{v}-v\Vert \end{array}$ (3.3)

和

$\begin{array}{c}\Vert {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}+v-\bar{v}\Vert =\alpha \Vert {\Pi }_{\Omega }\left(v-\alpha \left(F\left(\bar{v}\right)+{\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p}\right)\right)\\ -{\Pi }_{\Omega }\left(v-\alpha \left(F\left(v\right)+{\nabla }_{w}g\left(v,v\right)\bar{p}\right)\right)\Vert \end{array}$

$\begin{array}{c}\le \alpha \Vert \left(F\left(v\right)-F\left(\bar{v}\right)\right)+\left({\nabla }_w^{\text{T}}g\left(v,v\right)\bar{p}-{\nabla }_w^{\text{T}}g\left(\bar{v},\bar{v}\right)\bar{p}\right)\Vert \\ \le \alpha \left(\left|F\right|+C_0|\nabla |\right)\Vert \bar{v}-v\Vert \\ =\alpha C\Vert \bar{v}-v\Vert ,\end{array}$ (3.4)

其中 $C=\left|F\right|+C_0|\nabla |$。(3.3)和(3.4)在具有控制过程的二阶微分方程系统(3.1)的轨迹的收敛性定理证明过程中起着重要的作用。

通过投影算子的定义和引理2.1将微分方程系统(3.1)转换成下面的变分不等式组

$\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}+\alpha \left(F\left(\bar{v}\right)+{\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p}\right),w-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle \ge 0,\forall w\in \Omega ,$ (3.5)

$\langle {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\alpha g\left(\bar{v},\bar{v}\right),y-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle \ge 0,\forall y\in {\Re }_{+}^m,$ (3.6)

$\langle \bar{v}-v+\alpha \left(F\left(v\right)+{\nabla }_{w}g\left(v,v\right)\bar{p}\right),w-\bar{v}\rangle \ge 0,\forall w\in \Omega ,$ (3.7)

$\langle \bar{p}-p-\alpha g\left(v,v\right),y-\bar{p}\rangle \ge 0,\forall y\in {\Re }_{\text{+}}^m.$ (3.8)

下面证明具有控制过程的微分方程系统(3.1)的轨迹的聚点就是具有双约束条件的变分不等式(1.1)的解。

定理3.1：假设具有双约束条件的变分不等式(1.1)的解集非空，映射 $F:{\Re }^n\to {\Re }^n$ 是单调的和Lipschitz连续的，其Lipschitz常数为 $\left|F\right|$，映射 $g:{\Re }^n\times {\Re }^n\to {\Re }^m$ 是对称函数，且关于第二元w对任意v是可微的，且 ${g\left(v,w\right)|}_{v=w}$ 是凸的， ${g\left(v,w\right)|}_{v=w}$ 和 ${{\nabla }_w^{\text{T}}g\left(v,w\right)|}_{v=w}$ 都是Lipschitz连续，其Lipschitz常数分别为 $\left|g\right|$ 和 $|\nabla |$。假设当 $t\to \infty$ 时， $\Vert \bar{p}\left(t\right)\Vert \le C_0$，及当 $t\to \infty$ 时， $\Vert p\left(t\right)\Vert$， $\Vert \stackrel{\dot{}}{p}\left(t\right)\Vert$ 有界， $\Omega \subseteq {\Re }^n$ 是非空闭凸集合。当 $1<{\beta }_1<{\mu }_1<{\beta }_1^2,0<{\mu }_2<\frac{{\beta }_2^2}{2}$ 和 $0<\alpha <\frac{1}{\sqrt{2C^2+{\left|g\right|}^2}}$ 时，其中 $C=\left|F\right|+C_0|\nabla |$，具有控制过程的二阶微分方程系统(3.1)的轨迹的聚点是具有双约束条件的变分不等式(1.1)的解。

证明：在(3.5)中令 $w=v^{\ast }$，在(3.7)中令 $w=v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}$ 分别得到

$\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}+\alpha \left(F\left(\bar{v}\right)+{\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p}\right),v^{\ast }-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle \ge 0$ (3.9)

和

$\langle \bar{v}-v+\alpha \left(F\left(v\right)+{\nabla }_{w}g\left(v,v\right)\bar{p}\right),v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \ge 0.$ (3.10)

对(3.10)式子展开得到

$\begin{array}{l}\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\alpha \langle F\left(\bar{v}\right),v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \\ -\alpha \langle F\left(\bar{v}\right)-F\left(v\right),v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\alpha \langle {\nabla }_w^{}g\left(\bar{v},\bar{v}\right)\bar{p},v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \\ -\alpha \langle \left({\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p}-{\nabla }_{w}g\left(v,v\right)\bar{p}\right),v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \ge 0.\end{array}$ (3.11)

由内积与范数的关系及(3.4)，(3.11)计算后可以得到

$\begin{array}{l}\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\alpha \langle F\left(\bar{v}\right),v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \\ +\alpha \langle {\nabla }_{w}g\left(\bar{v},\bar{v}\right)\bar{p},v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +{\alpha }^2{C}^2{\Vert \bar{v}-v\Vert }^2\ge 0.\end{array}$ (3.12)

将(3.9)和(3.12)相加可得

$\begin{array}{l}\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v},v^{\ast }-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle +\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\alpha \langle F\left(\bar{v}\right),v^{\ast }-\bar{v}\rangle \\ +\alpha \langle \bar{p},{\nabla }_w^{\text{T}}g\left(\bar{v},\bar{v}\right)\left(v^{\ast }-\bar{v}\right)\rangle +{\alpha }^2{C}^2{\left|\bar{v}-v\right|}^2\ge 0.\end{array}$ (3.13)

由于映射 $g:{\Re }^n\times {\Re }^n\to {\Re }^m$ 是对称函数，且 ${g\left(v,w\right)|}_{v=w}$ 是凸的，根据性质2.2的(2.3)，(3.13)的第四项可以转化为

$\langle \bar{p},{\nabla }_w^{\text{T}}g\left(\bar{v},\bar{v}\right)\left(v^{\ast }-\bar{v}\right)\rangle =\frac{1}{2}\langle \bar{p},{\nabla }^{\text{T}}g\left(\bar{v},\bar{v}\right)\left(v^{\ast }-\bar{v}\right)\rangle \le \frac{1}{2}\langle \bar{p},g\left(v^{\ast },v^{\ast }\right)-g\left(\bar{v},\bar{v}\right)\rangle .$ (3.14)

将(3.14)代入(3.13)后可得

$\begin{array}{l}\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v},v^{\ast }-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle +\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\alpha \langle F\left(\bar{v}\right),v^{\ast }-\bar{v}\rangle \\ +\frac{\alpha }{2}\langle \bar{p},g\left(v^{\ast },v^{\ast }\right)-g\left(\bar{v},\bar{v}\right)\rangle +{\alpha }^2{C}^2{\Vert \bar{v}-v\Vert }^2\ge 0.\end{array}$ (3.15)

令(2.10)中第一式 $w=\bar{v}$ 然后加到(3.15)中得

$\begin{array}{l}\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v},v^{\ast }-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle +\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle \\ +\alpha \langle F\left(\bar{v}\right)-F\left(v^{\ast }\right),v^{\ast }-\bar{v}\rangle +\frac{\alpha }{2}\langle \bar{p}-p^{\ast },g\left(v^{\ast },v^{\ast }\right)-g\left(\bar{v},\bar{v}\right)\rangle +{\alpha }^2{C}^2{\Vert \bar{v}-v\Vert }^2\ge 0.\end{array}$ (3.16)

在(3.6)中令 $y=p^{\ast }$，在(3.8)中令 $y=p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}$ 分别得到

$\langle {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p},p^{\ast }-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle -\alpha \langle g\left(\bar{v},\bar{v}\right),p^{\ast }-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle \ge 0$ (3.17)

和

$\begin{array}{l}\langle \bar{p}-p,p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle +\alpha \langle g\left(\bar{v},\bar{v}\right)-g\left(v,v\right),p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle \\ -\alpha \langle g\left(\bar{v},\bar{v}\right),p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle \ge 0.\end{array}$ (3.18)

利用定理中的Lipschitz条件，运用(3.3)对上式中的第二项进行计算得到

$\langle \bar{p}-p,p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle -\alpha \langle g\left(\bar{v},\bar{v}\right),p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle +{\alpha }^2{\left|g\right|}^2{\Vert \bar{v}-v\Vert }^2\ge 0.$

将上式和(3.18)相加得到

$\begin{array}{l}\langle {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p},p^{\ast }-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle +\langle \bar{p}-p,p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle \\ -\alpha \langle g\left(\bar{v},\bar{v}\right),p^{\ast }-\bar{p}\rangle +{\alpha }^2{\left|g\right|}^2{\Vert \bar{v}-v\Vert }^2\ge 0,\end{array}$ (3.19)

由于 $\langle \bar{p},g\left(v^{\ast },v^{\ast }\right)\rangle \le 0,\langle p^{\ast },g\left(v^{\ast },v^{\ast }\right)\rangle =0$，则(3.19)式可以得到

$\begin{array}{l}\frac{1}{2}\langle {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p},p^{\ast }-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle +\frac{1}{2}\langle \bar{p}-p,p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle \\ +\frac{\alpha }{2}\langle g\left(v^{\ast },v^{\ast }\right)-g\left(\bar{v},\bar{v}\right),p^{\ast }-\bar{p}\rangle +\frac{1}{2}{\alpha }^2{\left|g\right|}^2{\Vert \bar{v}-v\Vert }^2\ge 0.\end{array}$ (3.20)

将(3.16)和(3.20)相加，又因为 $F\left(x\right)$ 是单调的映射，则有

$\begin{array}{l}\langle {\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v},v^{\ast }-v-{\mu }_1\ddot{v}-{\beta }_1\stackrel{\dot{}}{v}\rangle +\langle \bar{v}-v,v+{\mu }_1\ddot{v}+{\beta }_1\stackrel{\dot{}}{v}-\bar{v}\rangle +\frac{1}{2}\langle {\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p},p^{\ast }-p-{\mu }_2\ddot{p}-{\beta }_2\stackrel{\dot{}}{p}\rangle \\ +\frac{1}{2}\langle \bar{p}-p,p+{\mu }_2\ddot{p}+{\beta }_2\stackrel{\dot{}}{p}-\bar{p}\rangle +{\alpha }^2\left(\frac{1}{2}{\left|g\right|}^2+C^2\right){\Vert \bar{v}-v\Vert }^2\ge 0.\end{array}$

$\begin{array}{l}\frac{1}{2}{\mu }_1^2{\Vert \ddot{v}\Vert }^2+{\mu }_1{\beta }_1\langle \stackrel{\dot{}}{v},\ddot{v}\rangle +\frac{1}{2}{\beta }_1^2{\Vert \stackrel{\dot{}}{v}\Vert }^2+{\mu }_1\langle \ddot{v},v-v^{\ast }\rangle +{\beta }_1\langle \stackrel{\dot{}}{v},v-v^{\ast }\rangle \\ +\frac{1}{4}{\mu }_2^2{\Vert \ddot{p}\Vert }^2+\frac{1}{2}{\mu }_2{\beta }_2\langle \stackrel{\dot{}}{p},\ddot{p}\rangle +\frac{1}{4}{\beta }_2^2{\Vert \stackrel{\dot{}}{p}\Vert }^2+\frac{{\mu }_2}{2}\langle \ddot{p},p-p^{\ast }\rangle +\frac{{\beta }_2}{2}\langle \stackrel{\dot{}}{p},p-p^{\ast }\rangle \\ +\frac{1}{4}{\Vert \bar{p}-p\Vert }^2+\left(\frac{1}{2}-{\alpha }^2\left(C^2+\frac{1}{2}{\left|g\right|}^2\right)\right){\Vert \bar{v}-v\Vert }^2\le 0.\end{array}$ (3.21)

由下面关系

$\frac{1}{2}\frac{{\text{d}}^2}{\text{d}{t}^2}{\Vert v-v^{\ast }\Vert }^2={\Vert \stackrel{\dot{}}{v}\Vert }^2+\langle v-v^{\ast },\ddot{v}\rangle ,\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert \stackrel{\dot{}}{v}\Vert }^2=\langle \stackrel{\dot{}}{v},\ddot{v}\rangle ,\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert v-v^{\ast }\Vert }^2=\langle v-v^{\ast },\stackrel{\dot{}}{v}\rangle ,$

$\frac{1}{2}\frac{{\text{d}}^2}{\text{d}{t}^2}{\Vert p-p^{\ast }\Vert }^2={\Vert \stackrel{\dot{}}{p}\Vert }^2+\langle p-p^{\ast },\ddot{p}\rangle ,\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert \stackrel{\dot{}}{p}\Vert }^2=\langle \stackrel{\dot{}}{p},\ddot{p}\rangle ,\frac{1}{2}\frac{\text{d}}{\text{d}t}{\Vert p-p^{\ast }\Vert }^2=\langle p-p^{\ast },\stackrel{\dot{}}{p}\rangle .$

对(3.21)继续计算得到

$\begin{array}{l}\frac{{\mu }_1}{2}\frac{{\text{d}}^2}{\text{d}{t}^2}{\Vert v-v^{\ast }\Vert }^2+\frac{{\beta }_1}{2}\frac{\text{d}}{\text{d}t}{\Vert v-v^{\ast }\Vert }^2+\frac{{\mu }_1{\beta }_1}{2}\frac{\text{d}}{\text{d}t}{\Vert \stackrel{\dot{}}{v}\Vert }^2+\frac{1}{2}\left({\beta }_1^2-{\mu }_1\right){\Vert \stackrel{\dot{}}{v}\Vert }^2+\frac{{\mu }_1^2}{2}{\Vert \ddot{v}\Vert }^2\\ +\frac{{\mu }_2}{4}\frac{{\text{d}}^2}{\text{d}{t}^2}{\Vert p-p^{\ast }\Vert }^2+\frac{{\beta }_2}{4}\frac{\text{d}}{\text{d}t}{\Vert p-p^{\ast }\Vert }^2+\frac{{\mu }_2{\beta }_2}{4}\frac{\text{d}}{\text{d}t}{\Vert \stackrel{\dot{}}{p}\Vert }^2+\frac{1}{2}\left(\frac{{\beta }_2^2}{2}-{\mu }_2\right){\Vert \stackrel{\dot{}}{p}\Vert }^2+\frac{{\mu }_2^2}{4}{\Vert \ddot{p}\Vert }^2\\ +\left(\frac{1}{2}-{\alpha }^2\left(C^2+\frac{1}{2}{\left|g\right|}^2\right)\right){\Vert \bar{v}-v\Vert }^2+\frac{1}{4}{\Vert \bar{p}-p\Vert }^2\le 0.\end{array}$ (3.22)

根据已知条件 $0<{\mu }_1<{\beta }_1^2$， $0<{\mu }_2<\frac{{\beta }_2^2}{2}$， $0<\alpha <\frac{1}{\sqrt{2C^2+{\left|g\right|}^2}}$，因此 ${\beta }_1^2-{\mu }_1>0$， $\frac{{\beta }_2^2}{2}-{\mu }_2>0$ 和 $\frac{1}{2}-{\alpha }^2\left(C^2+\frac{1}{2}{\left|g\right|}^2\right)>0$。

在(3.22)中，令 $\varphi \left(v\right)=\frac{1}{2}{\Vert v-v^{\ast }\Vert }^2,\psi \left(p\right)=\frac{1}{4}{\Vert p-p^{\ast }\Vert }^2$，并对(3.22)各项从 $t_0$ 到t进行积分得

$\begin{array}{l}{\mu }_1\frac{\text{d}}{\text{d}t}\varphi \left(v\right)+{\beta }_1\varphi \left(v\right)+\frac{{\mu }_1{\beta }_1}{2}{\Vert \stackrel{\dot{}}{v}\Vert }^2+\frac{1}{2}\left({\beta }_1^2-{\mu }_1\right){\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{v}\Vert }^2\text{d}\tau }+\frac{{\mu }_1^2}{2}{\displaystyle {\int }_{t_0}^t{\Vert \ddot{v}\Vert }^2\text{d}\tau }\\ +{\mu }_2\frac{\text{d}}{\text{d}t}\psi \left(p\right)+{\beta }_2\psi \left(p\right)+\frac{{\mu }_2{\beta }_2}{4}{\Vert \stackrel{\dot{}}{p}\Vert }^2+\frac{1}{2}\left(\frac{{\beta }_2^2}{2}-{\mu }_2\right){\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{p}\Vert }^2\text{d}\tau }+\frac{{\mu }_2^2}{4}{\displaystyle {\int }_{t_0}^t{\Vert \ddot{p}\Vert }^2\text{d}\tau }\\ +\left(\frac{1}{2}-{\alpha }^2\left(C^2+\frac{1}{2}{\left|g\right|}^2\right)\right){\displaystyle {\int }_{t_0}^t{\Vert v-\bar{v}\Vert }^2\text{d}\tau }+\frac{1}{4}{\displaystyle {\int }_{t_0}^t{\Vert p-\bar{p}\Vert }^2\text{d}\tau }\le B,\end{array}$ (3.23)

其中B为常数如下表示

$B={\mu }_1\frac{\text{d}}{\text{d}t}\varphi \left(v_0\right)+{\beta }_1\varphi \left(v_0\right)+\frac{{\mu }_1{\beta }_1}{2}{\Vert {\stackrel{\dot{}}{v}}_0\Vert }^2+{\mu }_2\frac{\text{d}}{\text{d}t}\psi \left(p_0\right)+{\beta }_2\psi \left(p_0\right)+\frac{{\mu }_2{\beta }_2}{4}{\Vert {\stackrel{\dot{}}{p}}_0\Vert }^2.$

由于已知当 $t\to \infty$ 时， $\Vert p\left(t\right)\Vert$ 和 $\Vert \stackrel{\dot{}}{p}\left(t\right)\Vert$ 有界，而

$\left|\frac{\text{d}}{\text{d}t}\psi \left(p\right)\right|=\left|\langle \stackrel{\dot{}}{p},p-p^{\ast }\rangle \right|\le \Vert \stackrel{\dot{}}{p}\Vert \Vert p-p^{\ast }\Vert ,$

因此 $\left|\frac{\text{d}}{\text{d}t}\psi \left(p\right)\right|$ 是有界的。根据(3.23)可知，存在常数 $B_1$ 使得

${\mu }_1\frac{\text{d}}{\text{d}t}\varphi \left(v\right)+{\beta }_1\varphi \left(v\right)\le B_1,$ (3.24)

对(3.24)式又可以写作

${\mu }_1{\text{e}}^{-\frac{{\beta }_1}{{\mu }_1}t}\frac{\text{d}}{\text{d}t}\left({\text{e}}^{\frac{{\beta }_1}{{\mu }_1}t}\varphi \left(v\right)\right)\le B_1,$

即

$\frac{\text{d}}{\text{d}t}\left({\text{e}}^{\frac{{\beta }_1}{{\mu }_1}t}\varphi \left(v\right)\right)\le B_1\frac{1}{{\mu }_1}{\text{e}}^{\frac{{\beta }_1}{{\mu }_1}t},$ (3.25)

对(3.25)两边从 $t_0$ 到t进行积分得

${\text{e}}^{\frac{{\beta }_1}{{\mu }_1}t}\varphi \left(v\right)\le \frac{B_1}{{\beta }_1}{\text{e}}^{\frac{{\beta }_1}{{\mu }_1}t}+C_1,$

其中 $C_1$ 为常数。进一步整理得

$\varphi \left(v\right)\le \frac{B_1}{{\beta }_1}+C_1{\text{e}}^{-\frac{{\beta }_1}{{\mu }_1}t}.$ (3.26)

显然，(3.26)表明当 $t\to \infty$ 时， $\varphi \left(v\right)$ 有界。由于函数 $\varphi \left(v\right)=\frac{1}{2}{\Vert v-v^{\ast }\Vert }^2$，显然轨迹 $v\left(t\right)$ 也是有界的。存在常数 $B_2$，

$\Vert v\left(t\right)-v^{\ast }\Vert \le B_2.$ (3.27)

下证 ${\displaystyle {\int }_{t_0}^t{\Vert \ddot{v}\Vert }^2\text{d}\tau <\infty }$， ${\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{v}\Vert }^2\text{d}\tau }<\infty$， ${\displaystyle {\int }_{t_0}^t{\Vert \ddot{p}\Vert }^2\text{d}\tau }<\infty$， ${\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{p}\Vert }^2\text{d}\tau }<\infty$， ${\displaystyle {\int }_{t_0}^t{\Vert \bar{v}-v\Vert }^2\text{d}\tau }<\infty$，和 ${\displaystyle {\int }_{t_0}^t{\Vert \bar{p}-p\Vert }^2\text{d}\tau }<\infty$ 成立。

首先证明 $\Vert \stackrel{\dot{}}{v}\Vert$ 是有界的。由不等式(3.23)得

${\mu }_1\frac{\text{d}}{\text{d}t}\varphi \left(v\right)+{\beta }_1\varphi \left(v\right)+\frac{{\mu }_1{\beta }_1}{2}{\Vert \stackrel{\dot{}}{v}\Vert }^2\le B_3.$ (3.28)

其中 $B_3$ 为常数。

由于 $\varphi \left(v\right)=\frac{1}{2}{\Vert v-v^{\ast }\Vert }^2$，而 $\frac{\text{d}}{\text{d}t}\varphi \left(v\right)=\langle \stackrel{\dot{}}{v},v-v^{*}\rangle$，又因为

$\langle \stackrel{\dot{}}{v},v-v^{\ast }\rangle =-\frac{1}{2}{\Vert \stackrel{\dot{}}{v}\Vert }^2-\frac{1}{2}{\Vert v-v^{\ast }\Vert }^2+\frac{1}{2}{\Vert \stackrel{\dot{}}{v}+v-v^{\ast }\Vert }^2,$

则不等式(3.28)可以化简为，

$\frac{1}{2}\left({\beta }_1-{\mu }_1\right){\Vert v-v^{\ast }\Vert }^2+\frac{{\mu }_1}{2}\left({\beta }_1-1\right){\Vert \stackrel{\dot{}}{v}\Vert }^2\le B_3.$ (3.29)

由于 $1<{\beta }_1<{\mu }_1$，在由(3.27)可以得到 $\Vert \stackrel{\dot{}}{v}\Vert$ 是有界的，可以表示如下

$\frac{{\mu }_1}{2}\left({\beta }_1-1\right){\Vert \stackrel{\dot{}}{v}\Vert }^2\le B_3+\frac{1}{2}\left({\mu }_1-{\beta }_1\right){\Vert v-v^{\ast }\Vert }^2\le B_3+\frac{1}{2}\left({\mu }_1-{\beta }_1\right)B_2.$ (3.30)

由于 $\Vert \stackrel{\dot{}}{v}\Vert$ 是有界的，且 $\left|\frac{\text{d}}{\text{d}t}\varphi \left(v\right)\right|=\left|\langle \stackrel{\dot{}}{v},v-v^{\ast }\rangle \right|\le \Vert \stackrel{\dot{}}{v}\Vert \Vert v-v^{\ast }\Vert$，因此 $\frac{\text{d}}{\text{d}t}\varphi \left(v\right)$ 有界，根据(3.23)存在常数 $B_4$ 有

$\begin{array}{l}\frac{1}{2}\left({\beta }_1^2-{\mu }_1\right){\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{v}\Vert }^2\text{d}\tau }+\frac{{\mu }_1^2}{2}{\displaystyle {\int }_{t_0}^t{\Vert \ddot{v}\Vert }^2\text{d}\tau }+\frac{1}{2}\left(\frac{{\beta }_2^2}{2}-{\mu }_2\right){\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{p}\Vert }^2\text{d}\tau }+\frac{{\mu }_2^2}{4}{\displaystyle {\int }_{t_0}^t{\Vert \ddot{p}\Vert }^2\text{d}\tau }\\ +\left(\frac{1}{2}-{\alpha }^2\left(C^2+\frac{1}{2}{\left|g\right|}^2\right)\right){\displaystyle {\int }_{t_0}^t{\Vert v-\bar{v}\Vert }^2\text{d}\tau }+\frac{1}{4}{\displaystyle {\int }_{t_0}^t{\Vert p-\bar{p}\Vert }^2\text{d}\tau }\le B_4,\end{array}$ (3.31)

由不等式(3.31)可得：当 $t\to \infty$ 时，下式成立

$\begin{array}{l}{\displaystyle {\int }_{t_0}^t{\Vert \ddot{v}\Vert }^2\text{d}\tau <\infty },{\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{v}\Vert }^2\text{d}\tau }<\infty ,{\displaystyle {\int }_{t_0}^t{\Vert \ddot{p}\Vert }^2\text{d}\tau }<\infty ,\\ {\displaystyle {\int }_{t_0}^t{\Vert \stackrel{\dot{}}{p}\Vert }^2\text{d}\tau }<\infty ,{\displaystyle {\int }_{t_0}^t{\Vert \bar{v}-v\Vert }^2\text{d}\tau }<\infty ,{\displaystyle {\int }_{t_0}^t{\Vert \bar{p}-p\Vert }^2\text{d}\tau }<\infty .\end{array}$

假设存在一个常数 $\epsilon >0$，对所有的 $t\ge t_0$ 有， $\Vert \ddot{v}\left(t\right)\Vert \ge \epsilon$， $\Vert \ddot{p}\left(t\right)\Vert \ge \epsilon$， $\Vert \stackrel{\dot{}}{v}\left(t\right)\Vert \ge \epsilon$， $\Vert \stackrel{\dot{}}{p}\left(t\right)\Vert \ge \epsilon$， $\Vert \bar{v}\left(t\right)-v\left(t\right)\Vert \ge \epsilon$ 和 $\Vert \bar{p}\left(t\right)-p\left(t\right)\Vert \ge \epsilon$ 成立，这和上式的积分收敛矛盾。因此必存t的子序列 $t_i$，当 $i\to \infty$ 时， $\Vert \ddot{v}\left(t_i\right)\Vert \to 0$， $\Vert \ddot{p}\left(t_i\right)\Vert \to 0$， $\Vert \stackrel{\dot{}}{v}\left(t_i\right)\Vert \to 0$， $\Vert \stackrel{\dot{}}{p}\left(t_i\right)\Vert \to 0$， $\Vert \bar{v}\left(t_i\right)-v\left(t_i\right)\Vert \to 0$ 和 $\Vert \bar{p}\left(t_i\right)-p\left(t_i\right)\Vert \to 0$ 成立。又因为已证得 $v\left(t\right)$ 和 $p\left(t\right)$ 都是有界的，可知 $v\left(t_i\right)$ 和 $p\left(t_i\right)$ 也是有界的。取 $t_i$ 的子序列 $t_{i_j}$，则必存在 $v\prime$ 和 $p\prime$，当 $j\to \infty$ 时， $v\left(t_{i_j}\right)\to v\prime$， $p\left(t_{i_j}\right)\to p\prime$，且依然有 $\Vert \ddot{v}\left(t_{i_j}\right)\Vert \to 0$， $\Vert \ddot{p}\left(t_{i_j}\right)\Vert \to 0$， $\Vert \stackrel{\dot{}}{v}\left(t_{i_j}\right)\Vert \to 0$， $\Vert \stackrel{\dot{}}{p}\left(t_{i_j}\right)\Vert \to 0$， $\Vert \bar{v}\left(t_{i_j}\right)-v\left(t_{i_j}\right)\Vert \to 0$ 和 $\Vert \bar{p}\left(t_{i_j}\right)-p\left(t_{i_j}\right)\Vert \to 0$ 成立。

在微分方程系统(3.1)和(3.2)中取 $t_{i_j}$，当 $j\to \infty$ 时得到

$\begin{array}{l}{v}^{\prime }={\Pi }_{\Omega }\left(v^{\prime }-\alpha \left(F\left(v^{\prime }\right)+{\nabla }_{w}g\left(v^{\prime },v^{\prime }\right)p^{\prime }\right)\right),\\ p^{\prime }={\Pi }_{+}\left(p^{\prime }+\alpha g\left(v^{\prime },v^{\prime }\right)\right),\end{array}$

上式与(2.11)一致，这就说明 $v\prime$ 是具有双约束条件的变分不等式(1.1)的解。证毕。

4. 数值结果

本节，我们将通过具有控制过程的二阶微分方程系统(3.1)求解两个具有双约束条件的变分不等式，以验证该方法的有效性。应用Matlab R2019a软件进行计算。在求解的过程中, 所采用的具体算法是微分方程求解函数ode45，这个函数采用的是四阶五级的Runge-Kutta方法。计算机的配置为：CPU Intel(R) Core(TM) i7-7700HQ @2.80 GHz；内存为16.0 GB。

例1考虑双约束变分不等式问题

$\langle F\left(v\right),w-v\rangle \ge 0,w\in {\Re }^3,g\left(v,w\right)\le 0,$ (4.1)

其中

$F\left(v\right)=\left(\begin{array}{c}-v_2{v}_3\\ -v_1{v}_3\\ -v_1{v}_2\end{array}\right),g\left(v,w\right)=\frac{1}{2}{v}_1^2+\frac{1}{2}{v}_2^2+2v_3^2+\frac{1}{2}{w}_1^2+\frac{1}{2}{w}_2^2+2w_3^2-48.$

其解为 $v^{*}={\left(4.0000,\mathrm{2.8200.2.0000}\right)}^{\text{T}}$。

图1描绘了具有双约束变分条件的不等式问题(4.1)的具有控制过程的二阶微分方程系统(4.19)的轨迹随时间的变化关系，其中该图的曲线是微分方程系统(3.1)的轨迹从三个不同的初始点生成。微分方程系统(3.1)的轨迹 $v={\left(v_1,v_2,v_3\right)}^{\text{T}}$ 收敛于点 $v^{*}={\left(4.0000,\mathrm{2.8284.2.0000}\right)}^{\text{T}}$，即问题(4.1)的近似解。

例2考虑双约束变分不等式问题

$\langle F\left(v\right),w-v\rangle \ge 0\text{,}w\in {\Re }^2,g\left(v,w\right)\le 0,$ (4.2)

其中，

$F\left(v\right)=\left(\begin{array}{c}\frac{\pi }{12}\cos \left(\frac{\pi v_1}{12}\right)\cos \left(\frac{\pi v_2}{6}\right)\\ -\frac{\pi }{16}\sin \left(\frac{\pi v_2}{16}\right)\sin \left(\frac{\pi v_1}{12}\right)\end{array}\right),g\left(v,w\right)=-2v_1+\frac{3}{2}{v}_2-2w_1+\frac{3}{2}{w}_2.$

其解为 $v^{*}={\left(-3.0000,-4.0000\right)}^{\text{T}}$。

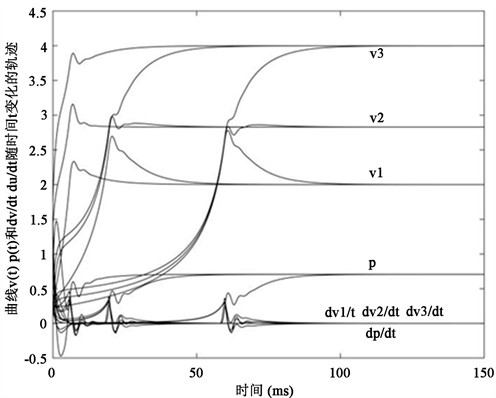
Figure 1. Trajectories convergence of the second-order differential equation system with the control process (3.1) for solving problem (4.1)

图1. 问题(4.1)的具有控制过程的二阶微分方程系统(3.1)的轨迹的收敛性

图2描绘了具有双约束变分条件的不等式问题(4.2)的具有控制过程的二阶微分方程系统(3.1)的轨迹随时间的变化关系，其中该图的曲线是微分方程系统(3.1)的轨迹从三个不同的初始点生成。微分方程系统(3.1)的轨迹 $v={\left(v_1,v_2\right)}^{\text{T}}$ 收敛于点 $v^{*}={\left(-2.9994,-3.9992\right)}^{\text{T}}$，即问题(4.2)的近似解。

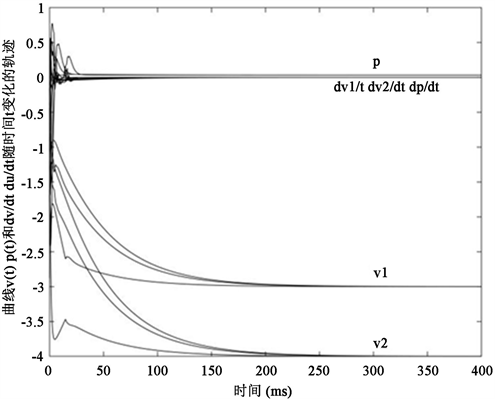
Figure 2. Trajectories convergence of the second-order differential equation system with the control process (3.1) for solving problem (4.2)

图2. 问题(4.2)的具有控制过程的二阶微分方程系统(3.1)的轨迹的收敛性

5. 结论

本文首先介绍了双约束条件的对称函数的定义和性质，将具有双约束条件的变分不等式看作一类特殊的优化问题，利用其拉格朗日函数和投影算子的定义和性质，得到了双约束变分不等式的等价投影算子方程组。在通过该算子方程组建立了求解具有双约束条件的变分不等式的具有控制过程的二阶微分方程系统，并证明了该二阶微分方程系统的聚点是具有双约束条件的变分不等式的解。二阶微分方程系统的建立后，与Antipin [1] 不同，本文给出了两个算例说明该方法的有效性。

此外，运用本微分方程方法可以用来求解优化问题、不动点问题等也是一个值得研究的方向。

基金项目

国家自然科学基金青年基金(编号：11801381)。