(3+1)维KP-Boussinesq和BKP-Boussinesq方程的精确行波解

Exact Traveling Wave Solutions and Bifurcation for (3+1) Dimensional KP-Boussinesq and BKP-Boussinesq Equations

摘要: 本文借助平面动力系统分支理论以及Hamilton能量函数研究(3+1)维KP-Boussinesq和BKP-Boussinesq方程。得到了这两类方程行波解的所有分支、相图，同时计算出了所有行波解的精确参数表达式以及参数条件。该文得到这两类方程的行波包括亮、暗孤子、周期波、扭子波以及一些其它类型的波。

Abstract: In this paper, the (3+1) dimensional KP-Boussinesq and BKP-Boussinesq equations are studied by using the bifurcation theory of planar dynamical systems and Hamilton energy functions. All the branches and phase diagrams of the traveling wave solutions of these two equations are obtained, and the exact parameter expressions and parameter conditions of all the traveling wave solutions are also calculated. In the paper, the traveling wave solutions of these two equations are obtained, including solitary wave solutions, periodic wave solutions and kink wave solutions.

1. 引言

现代科学中，非线性现象在科学和工程的许多领域中都存在，如固体物理学、弹性力学、离子体物理学、流体力学、气体动力学、化学反应、生态学等，这些现象本质上都是由非线性发展方程支配的。在最近的几十年中，Boussinesq方程激起了广大物理学和数学工作者的广泛兴趣。其中寻求精确波解显得尤为重要，精确波解有助于提供关于复杂物理现象结构的信息。因此探索非线性发展方程的精确波解成为非线性物理现象研究中的一项重要课题。为此建立了许多方法，如Jacobi椭圆函数法 [1]，齐次平衡法 [2]，改进的简单方程法 [3]，G'/G-展开法 [4]，改进的G'/G展开法 [5]，同伦摄动法 [6]，变分法 [7]，非摄动法 [8] 等，值得一提的是目前没有唯一的一种方法可以解决所有类型的非线性发展方程的精确波解。最近文 [9] 中利用Hirota双线性方法结合微扰展开技术，得到了(3+1)维KP-Boussinesq一般的高阶孤子解。文 [10] 中利用齐次平衡法，得到了WBK方程以及一些其它类型的非线性发展方程的精确解。该文将借助文献 [11] [12] [13] [14] 中发展的动力系统分支方法研究(3+1)维KP-Boussinesq和BKP-Boussinesq方程，得到两类方程行波解的所有分支情况，相图以及参数条件，同时得到所有行波解的精确参数表达式。

广义的(3+1)维KP-Boussinesq方程一般形式为

$u_{xxxy}+3{\left(u_x{u}_y\right)}_x+u_{tx}+u_{ty}-u_{zz}=0$ (1.1)

和BKP方程一般形式为

$u_{ty}-u_{xxxy}-3{\left(u_x{u}_y\right)}_x+3u_{xx}=0$ (1.2)

为了求解方程(1.1)和(1.2)的行波解，引入行波变量 $\xi =\alpha x+\beta y+\gamma z-ct$，c是波速，代入(1.1)且等式两边关于 $\xi$ 积分一次得到

${\alpha }^3\beta u^{\left(3\right)}\left(\xi \right)+3{\alpha }^2\beta u^{\prime }{\left(\xi \right)}^2-\left(\alpha c+\beta c+{\gamma }^2\right)u^{\prime }\left(\xi \right)=0$ (1.3)

代入(1.2)且等式两边关于 $\xi$ 积分一次得到

${\alpha }^3\beta u^{\left(3\right)}\left(\xi \right)+3{\alpha }^2\beta u^{\prime }{\left(\xi \right)}^2+\left(\beta c-3{\alpha }^2\right)u^{\prime }\left(\xi \right)=0$ (1.4)

假设 $\alpha \ne 0$， $\beta \ne 0$，令 $\phi \left(\xi \right)=\frac{\text{d}u\left(\xi \right)}{\text{d}\xi }$，即 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$。记

$A=\frac{3}{\alpha }\left(A\ne 0\right),B=-\frac{\alpha c+\beta c+{\gamma }^2}{{\alpha }^3\beta },C=\frac{\beta c-3{\alpha }^2}{{\alpha }^2\beta }$

分别代入 $A,B,C$ 到(1.3)，(1.4)中得到：

${\phi }^{\left(2\right)}\left(\xi \right)+A\phi {\left(\xi \right)}^2+B\phi \left(\xi \right)=0$ (1.5)

和

${\phi }^{\left(2\right)}\left(\xi \right)+A\phi {\left(\xi \right)}^2+C\phi \left(\xi \right)=0$ (1.6)

明显的，只要作变换 $B\leftrightarrow C$，则方程(1.5)和(1.6)是等价的。从而接下来我们只需要讨论方程(1.5)

行波解的分支情况以及精确表达式，就能知道方程(1.6)的相关结论。

2. 方程(1.5)的行波解分支

对于方程(1.5)，令 ${\phi }^{\prime }\left(\xi \right)=y$，得到如下的平面自治行波系统：

${\phi }^{\prime }\left(\xi \right)=y,y^{\prime }=-A\phi {\left(\xi \right)}^2-B\phi \left(\xi \right)$ (2.1)

系统(2.1)有如下的首次积分：

$H\left(\phi ,y\right)=\frac{1}{2}{y}^2+\frac{1}{3}A{\phi }^3+\frac{1}{2}B{\phi }^2=h$ (2.2)

其中h是积分常数。当 $B=0$ 时，系统(2.1)只有一个平衡点 $\left(0,0\right)$。当 $B\ne 0$ 时，系统(2.1)有两个平衡点

$\left(0,0\right),\left(-\frac{B}{A},0\right)$。用 $J\left(P\right)$ 表示系统(2.1)的线性化系统在平衡点P的雅可比行列式，计算可得 $J\left(0,0\right)=-B$， $J\left(-\frac{B}{A},0\right)=-3B$。根据平面微分系统分支理论，得到二维平面系统(2.1)的分支情况以及相图，见图1~6。

从系统(2.1)的相图可以看出，图1~4中分别有围绕中心的一族周期波轨道，以及在鞍点处存在同宿轨道。下面逐一计算出方程(1.5)所有行波解 $\phi \left(\xi \right)$ 的精确表达式，从而得到方程(1.3)的所有行波解 $u\left(\xi \right)$ 的精确表达式。

Figure 1. $A>0,B>0$

图1. $A>0,B>0$

Figure 2. $A>0,B<0$

图2. $A>0,B<0$

Figure 3. $A<0,B>0$

图3. $A<0,B>0$

Figure 4. $A<0,B<0$

图4. $A<0,B<0$

Figure 5. $A>0,B=0$

图5. $A>0,B=0$

Figure 6. $A<0,B=0$

图6. $A<0,B=0$

3. 方程(1.5)所有行波解的精确表达式

1) 当 $A>0,B>0$ 时，对应于图1。计算可得 $h_0=H\left(0,0\right)=0,h_1=H\left(-\frac{B}{A},0\right)=\frac{B^3}{6A^2}$。此时平衡点 $\left(0,0\right)$ 是中心，平衡点 $\left(-\frac{B}{A},0\right)$ 是鞍点。

a) 当 $0<h<h_1$ 时， $H\left(\phi ,y\right)=h$ 定义的是围绕中心平衡点 $\left(0,0\right)$ 的一族周期轨道。此时

$y^2=\frac{2}{3}A\left(-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}+\frac{3h}{A}\right)=\frac{2}{3}A\left(r_3-\phi \right)\left(\phi -r_2\right)\left(\phi -r_1\right)$ (3.1)

其中 $r_1,r_2,r_3$ 是方程 $-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}+\frac{3h}{A}=0$ 的三个实根，且满足 $r_1<r_2<0<r_3$。代入(3.1)到系统(2.1)的第一式且沿着周期轨积分得到：

$\sqrt{\frac{2A}{3}}\xi ={\displaystyle {\int }_{\phi }^{r_3}\frac{1}{\sqrt{\left(r_3-s\right)\left(s-r_2\right)\left(s-r_1\right)}}\text{d}s}=\frac{2}{\sqrt{r_3-r_1}}EllipticF\left(\sqrt{\frac{r_3-\phi }{r_3-r_2}},\sqrt{\frac{r_3-r_2}{r_3-r_1}}\right)$

其中 $EllipticF\left(\cdot ,\cdot \right)$ 是第一类椭圆积分。求解上式得到：

$\phi \left(\xi \right)=\left(r_2-r_3\right)sn{\left(\frac{\sqrt{6A}}{6}\sqrt{r_3-r_1}\xi ,\sqrt{\frac{r_3-r_2}{r_3-r_1}}\right)}^2+r_3$ (3.2)

由假设 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=r_3+\frac{\sqrt{6}}{\sqrt{A}}\frac{r_1-r_3}{\sqrt{r_3-r_1}}\left[\frac{\sqrt{6A\left(r_3-r_1\right)}}{6}\xi -EllipticE\left(sn\left(\frac{\sqrt{6A\left(r_3-r_1\right)}}{6}\xi ,\frac{\sqrt{r_3-r_2}}{\sqrt{r_3-r_1}}\right),\frac{\sqrt{r_3-r_2}}{\sqrt{r_3-r_1}}\right)\right]$ (3.3)

现不妨取 $A=B=1,h=\frac{B^3}{8A^2}=\frac{1}{8}$， $\phi =\phi \left(\xi \right),u=u\left(\xi \right)$ 的图像如图7、图8所示。

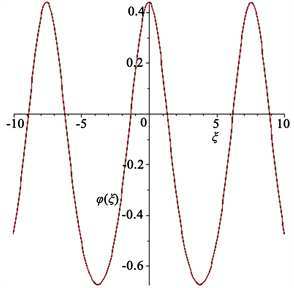
Figure 7. Periodic wave solution of $\phi =\phi (\; \xi \; )$

图7. 周期波解 $\phi =\phi (\; \xi \; )$

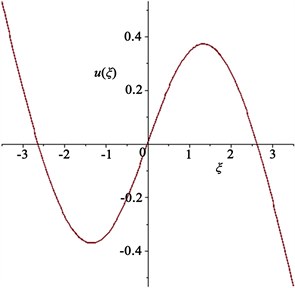
Figure 8. The 2D-Plot of $u=u(\; \xi \; )$

图8. $u=u\left(\xi \right)$ 的平面图像

b) 当 $h=h_1=\frac{B^3}{6A^2}$ 时， $H\left(\phi ,y\right)=h$ 定义的是满足 $\phi \left(\pm \infty \right)=-\frac{B}{A}$ 的一条同宿轨道。此时

$y^2=\frac{2}{3}A\left(-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}+\frac{3h}{A}\right)=\frac{2}{3}A\left(\frac{B}{2A}-\phi \right){\left(\phi +\frac{B}{A}\right)}^2$ (3.4)

代入(3.4)到系统(2.1)的第一式且沿着同宿轨道积分得到：

$\phi \left(\xi \right)=\frac{B\left[1-3\tanh {\left(\frac{1}{2}\sqrt{B}\xi \right)}^2\right]}{2A}$ (3.5)

由假设 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=\frac{3\sqrt{B}}{A}\tanh \left(\frac{1}{2}\sqrt{B}\xi \right)+\frac{3\sqrt{B}}{2A}\ln \left(\left|\frac{\tanh \left(\frac{1}{2}\sqrt{B}\xi \right)-1}{\tanh \left(\frac{1}{2}\sqrt{B}\xi \right)+1}\right|\right)+\frac{B}{2A}\xi$ (3.6)

现不妨取 $A=B=1,h=\frac{B^3}{8A^2}=\frac{1}{8}$， $\phi =\phi \left(\xi \right),u=u\left(\xi \right)$ 的图像如图9、图10所示。

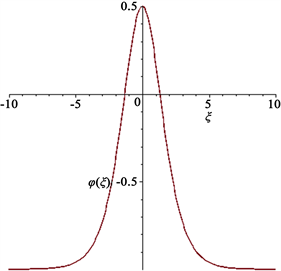
Figure 9. The bright soliton of $\phi =\phi (\; \xi \; )$

图9. 亮孤子 $\phi =\phi (\; \xi \; )$

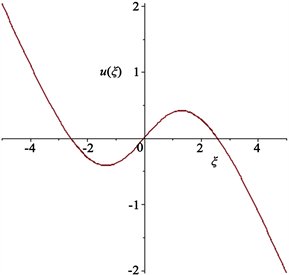
Figure 10. The 2D-plot of $u=u(\; \xi \; )$

图10. $u=u\left(\xi \right)$ 的平面图像

2) 当 $A>0,B<0$ 时，对应于图2。计算可得 $h_0=H\left(0,0\right)=0,h_1=H\left(-\frac{B}{A},0\right)=\frac{B^3}{6A^2}<0$。此时平衡点 $\left(0,0\right)$ 是鞍点，平衡点 $\left(-\frac{B}{A},0\right)$ 是中心。

a) 当 $h=h_0=0$ 时， $H\left(\phi ,y\right)=h$ 定义的是满足 $\phi \left(\pm \infty \right)=0$ 的一条同宿轨道。此时

$y^2=\frac{2}{3}A\left(-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}\right)=\frac{2}{3}A{\phi }^2\left(-\frac{3B}{2A}-\phi \right)$ (3.7)

代入(3.7)到方程(2.1)的第一式且沿着同宿轨道积分得到：

$\phi \left(\xi \right)=\frac{-6B{\text{e}}^{\sqrt{-B}\xi }}{A\left({\text{e}}^{2\sqrt{-B}\xi }+2{\text{e}}^{\sqrt{-B}\xi }+1\right)}$ (3.8)

由假设 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=\frac{6B}{A\sqrt{-B}\left({\text{e}}^{\sqrt{-B}\xi }+1\right)}$ (3.9)

现不妨取 $A=1,B=-2$， $\phi =\phi \left(\xi \right),u=u\left(\xi \right)$ 的图像如图11、图12所示。

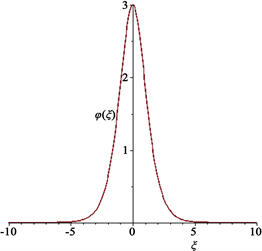
Figure 11. The bright soliton of $\phi =\phi (\; \xi \; )$

图11. 亮孤子 $\phi =\phi (\; \xi \; )$

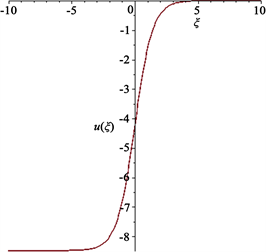
Figure 12. The kink wave solution of $u=u(\; \xi \; )$

图12. 扭子波 $u=u(\; \xi \; )$

b) 当 $h_1<h<0$ 时， $H\left(\phi ,y\right)=h$ 定义的是围绕中心平衡点 $\left(-\frac{B}{A},0\right)$ 的一族周期轨道。此时

$y^2=\frac{2}{3}A\left(-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}+\frac{3h}{A}\right)=\frac{2}{3}A\left(r_3-\phi \right)\left(\phi -r_2\right)\left(\phi -r_1\right)$ (3.10)

其中 $r_1,r_2,r_3$ 是方程 $-{\phi }^3-\frac{3}{2}\frac{B{\phi }^2}{A}+\frac{3h}{A}=0$ 的三个实根，且满足 $r_1<0<r_2<r_3$。 $\phi \left(\xi \right),u\left(\xi \right)$ 的表达式分别为(3.2)，(3.3)， $\phi \left(\xi \right)$ 是周期波解。

3) 当 $A<0,B>0$ 时，对应于图3。计算可得 $h_0=H\left(0,0\right)=0,h_1=H\left(-\frac{B}{A},0\right)=\frac{B^3}{6A^2}>0$。此时平衡点 $\left(0,0\right)$ 是中心，平衡点 $\left(-\frac{B}{A},0\right)$ 是鞍点。

a) 当 $0<h<h_1$ 时， $H\left(\phi ,y\right)=h$ 定义的是围绕中心 $\left(0,0\right)$ 的一族周期轨道，此时

$y^2=-\frac{2}{3}A\left({\phi }^3+\frac{3}{2}\frac{B{\phi }^2}{A}-\frac{3h}{A}\right)=-\frac{2}{3}A\left(\phi -r_3\right)\left(\phi -r_2\right)\left(\phi -r_1\right)$ (3.11)

其中 $r_1,r_2,r_3$ 是方程 ${\phi }^3+\frac{3}{2}\frac{B{\phi }^2}{A}-\frac{3h}{A}=0$ 的三个实根，且满足 $r_1<0<r_2<r_3$。代入(3.11)到系统(2.1)的第一式且沿着周期轨积分得到：

$\sqrt{-\frac{2A}{3}}\xi ={\displaystyle {\int }_{\phi }^{r_2}\frac{1}{\sqrt{\left(s-r_3\right)\left(s-r_2\right)\left(s-r_1\right)}}\text{d}s}$

求解积分得到：

$\phi \left(\xi \right)=\left(r_2-r_1\right)sn{\left(\frac{\sqrt{-6A}}{6}\sqrt{r_3-r_1}\xi ,\sqrt{\frac{r_2-r_1}{r_3-r_1}}\right)}^2+r_1$ (3.12)

由假设 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=r_1+\frac{\sqrt{6\left(r_3-r_1\right)}}{\sqrt{-A}}\left[\frac{\sqrt{6A\left(r_1-r_3\right)}}{6}\xi -EllipticE\left(sn\left(\frac{\sqrt{6A\left(r_1-r_3\right)}}{6}\xi ,\frac{\sqrt{r_2-r_1}}{\sqrt{r_3-r_1}}\right),\frac{\sqrt{r_2-r_1}}{\sqrt{r_3-r_1}}\right)\right]$ (3.13)

b) 当 $h=h_1=\frac{B^3}{6A^2}$ 时， $H\left(\phi ,y\right)=h$ 定义的是连接鞍点 $\left(-\frac{B}{A},0\right)$ 的一条同宿轨道。此时

$y^2=-\frac{2}{3}A\left({\phi }^3+\frac{3}{2}\frac{B{\phi }^2}{A}-\frac{3h}{A}\right)=-\frac{2}{3}A\left(\phi -\frac{B}{2A}\right){\left(\phi +\frac{B}{A}\right)}^2$ (3.14)

代入(3.14)到系统(2.1)的第一式且沿着同宿轨道积分得到：

$\phi \left(\xi \right)=-\frac{B}{A}\frac{{\left({\text{e}}^{\sqrt{B}\xi }-2\right)}^2}{{\left({\text{e}}^{\sqrt{B}\xi }+1\right)}^2}$ (3.15)

由假设 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=\sqrt{-\frac{B}{A}}\frac{{\text{e}}^{\sqrt{B}\xi }\ln \left({\text{e}}^{\sqrt{B}\xi }\right)+\ln \left({\text{e}}^{\sqrt{B}\xi }\right)+6}{{\text{e}}^{\sqrt{B}\xi }+1}$ (3.16)

其中 $\phi =\phi \left(\xi \right)$ 是暗孤子。

4) 当 $A<0,B<0$ 时，对应于图4。计算可得 $h_0=H\left(0,0\right)=0,h_1=H\left(-\frac{B}{A},0\right)=\frac{B^3}{6A^2}<0$。此时平衡点 $\left(0,0\right)$ 是鞍点，平衡点 $\left(-\frac{B}{A},0\right)$ 是中心。

a) 当 $h=h_0=0$ 时， $H\left(\phi ,y\right)=h$ 定义的是连接鞍点 $\left(0,0\right)$ 一条同宿轨道。此时

$y^2=-\frac{2}{3}A\left({\phi }^3+\frac{3}{2}\frac{B{\phi }^2}{A}\right)=-\frac{2}{3}A{\phi }^2\left(\phi +\frac{3B}{2A}\right)$ (3.17)

由(3.7)和系统(2.1)的第一式且沿着同宿轨道积分得到：

$\phi \left(\xi \right)=\frac{-6B{\text{e}}^{-\sqrt{-B}\xi }}{A\left({\text{e}}^{-2\sqrt{-B}\xi }+2{\text{e}}^{-\sqrt{-B}\xi }+1\right)}$ (3.18)

由(3.18)以及 $u\left(\xi \right)={\displaystyle \int \phi \left(\xi \right)\text{d}\xi }$，得到：

$u\left(\xi \right)=\frac{6B}{A\sqrt{-B}\left({\text{e}}^{\sqrt{-B}\xi }+1\right)}$ (3.19)

现不妨取 $A=-1,B=-1$， $\phi =\phi \left(\xi \right),u=u\left(\xi \right)$ 的图像见图13、图14。

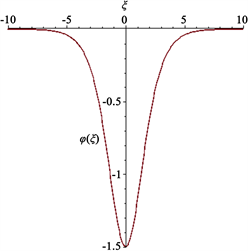
Figure 13. The dark soliton of $\phi =\phi (\; \xi \; )$

图13. 暗孤子 $\phi =\phi (\; \xi \; )$

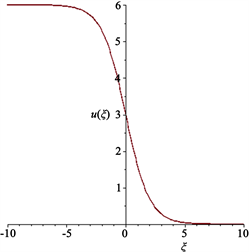
Figure 14. The kink wave solution of $u=u(\; \xi \; )$

图14. 扭子波 $u=u(\; \xi \; )$

b) 当 $h_1<h<0$ 时， $H\left(\phi ,y\right)=h$ 定义的是一族围绕中心 $\left(-\frac{B}{A},0\right)$ 的周期轨道，且有：

$y^2=-\frac{2}{3}A\left({\phi }^3+\frac{3}{2}\frac{B{\phi }^2}{A}-\frac{3h}{A}\right)=-\frac{2}{3}A\left(\phi -r_3\right)\left(\phi -r_2\right)\left(\phi -r_1\right)$ (3.20)

其中 $r_1<r_2<0<r_3$。此时 $\phi \left(\xi \right),u\left(\xi \right)$ 的表达式分别为(3.12)、(3.13)， $\phi \left(\xi \right)$ 是周期波解。

4. 结束语

应用发展的动力系统分支方法以及Hamilton能量函数，文中得到了(3+1)维KP-Boussinesq方程在不同参数条件下所有行波解的精确表达式，文中由公式(3.2)、(3.3)、(3.5)、(3.6)、(3.8)、(3.9)、(3.12)、(3.13)、(3.15)、(3.16)、(3.18)、(3.19)给出，由这些公式可知这其中包括周期波，亮、暗孤子，扭子波，以及一些其它类型的行波。此外，BKP-Boussinesq方程有与(3+1)维KP-Boussinesq方程完全类似的行波解。

基金项目

国家自然科学基金(11872197)、2021年江西省研究生创新专项资金项目(YC2021-S688)资助。

NOTES

^*通讯作者。