1. 引言
近年来随着城市的快速发展,工业废水、农业污染、城市生活污水等使得水资源的污染加重,由水体富营养化引起的破坏水生生态系统的现象时有发生。水体富营养化对浮游生物和鱼类都产生了很大的影响,不仅破坏了水生生态系统的平衡和稳定,也影响了水产养殖业的经济效益。因此,调节水生生态系统中各种群之间的相互作用关系,对于维持系统的平衡和稳定具有重要意义。
具有状态反馈脉冲效应的常微分方程被称为半连续动力系统 [1]。近年来,半连续动力系统在科学领域的应用越来越广泛 [2] - [12]。在调控生态系统的过程中,很多学者都通过脉冲状态反馈控制的方法来调节系统的平衡和稳定。例如,Zhang等人提出了一个考虑营养利用率的食饵捕食模型,并通过状态反馈脉冲控制来调节养殖水体的生态平衡 [4]。Guo等人提出并研究了脉冲放鱼和脉冲喷洒杀藻剂的藻鱼系统 [5]。Fu和Chen研究了具有两个状态依赖脉冲控制的水葫芦生态系统,讨论了阶一周期解和阶二周期解的存在性和稳定性 [6]。在此基础上,本文则提出了一个污染水体中具有脉冲状态反馈控制且捕食种群具有常数投放率的食饵捕食系统。
论文其余部分的组织如下。在第二节中,我们将介绍捕食种群具有常数投放率的自由发展模型和相应的状态反馈脉冲模型。在第三节中,对自由发展模型进行了定性分析,并分情况讨论了脉冲状态反馈控制模型的动力学性能。最后一节给出了一些数值模拟并说明了生物学意义。
2. 建立模型
2.1. 自由发展模型
首先我们考虑如下模型。
(2.1)
假设
分别表示t时刻食饵(浮游动植物)和捕食者(鱼类)的种群密度;浮游动植物以
的速率增长(其中
),
是食饵的环境容纳量,且食饵受到自身密度的制约,即随着食饵数量的增加食饵的增长速率逐渐减缓;
为鱼类对浮游动植物的捕食率;h为鱼类捕食的浮游动植物吸收转化为可存活的鱼类后代的比率;f为水污染导致的鱼类的死亡率;u为鱼类种群的常数投放率。
2.2. 状态反馈脉冲模型
由于水体受有机物污染后,会发生生物降解作用,在分解过程中消耗水中的氧气,使水中的氧气量降低,导致鱼类等会因缺氧而死亡。同时鱼类种群数量减少也会导致水体中浮游动植物大量繁殖;为达到一定的产鱼量,同时也为了避免水华的产生,需要常量投放一些鱼苗来补充受水污染影响而死亡的鱼类数量。但当鱼类种群数量过多时,水体的浮游动植物又不能满足鱼类对食物的需求,所以我们会通过状态反馈脉冲控制的方法捕捞成鱼,进而保持食饵捕食系统的稳定,同时也能产生经济效益。设阈值为m,则得到状态反馈脉冲系统为:
(2.2)
当鱼类数量小于m时,食饵捕食系统按照系统(2.2)的前两个方程发展。当鱼类种群数量达到m时,开始以
为收获率收获成鱼。根据实际的生物意义,下面的内容我们只考虑系统(2.2)在区域
的情况。
3. 模型分析
3.1. 自由发展模型(2.1)的定性分析
模型(2.1)满足如下方程:
(3.1)
它的垂直等倾线为
和
,水平等倾线为
。解方程组(3.1)可知,若
,则系统(2.1)存在一个边界平衡点
和一个正平衡点
,其中
,
。接下来,我们假设
总是成立。
下面分析平衡点
和
的稳定性。系统(2.1)的雅可比矩阵为:
.
系统(2.1)在
点的雅可比矩阵为:
.
经计算可得
,即
是一个鞍点。
系统(2.1)在
点的雅可比矩阵为:
.
经计算可得
,
.
显然,点E是一个局部渐进稳定的结点或焦点。
因此,得到结论如下。
定理1若
,则模型(2.1)的边界平衡点
是一个鞍点,正平衡点
是一个局部渐近稳定的结点或焦点。
接下来讨论系统(2.1)在平衡点E处的全局渐近稳定性。
首先,构造一个Lyapunov函数:
(3.2)
此函数沿着时间的导数计算为:
(3.3)
考虑平衡点方程:
(3.4)
将方程(3.4)带入(3.3)可得:
(3.5)
当
时,有
,故
在第一象限是负定的。
因此,我们得到如下结论。
定理2系统(2.1)在平衡点
处是全局渐进稳定的。
3.2. 模型(2.2)的阶一周期解的存在唯一性
根据上述分析,可知系统(2.1)的平衡点E是一个全局渐进稳定的结点或焦点(如图1所示)。接下来我们将要讨论当平衡点E是焦点时,系统(2.2)是否存在阶1周期解以及阶1周期解的唯一性。

Figure 1. Phase diagram of system (2.1). 1)
be a node point; 2)
be a focus point
图1. 系统(2.1)的相图。1)
是一个结点;2)
是一个焦点
情况1.
当
时,直线
落在平衡点
的下方,我们有如下结论。
定理3当
为焦点且
时,系统(2.2)存在一个唯一的阶1周期解。
证明:令直线
分别与水平等倾线和垂直等倾线交于
,
两点(如图2所示)。
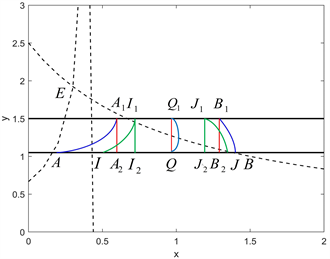
Figure 2. The existence and uniqueness of order-1 periodic solution for
图2.
时阶一周期解的存在和唯一性
首先,我们证明阶一周期解的存在性。从点A出发的轨迹交脉冲集M于点A1,然后经过脉冲效应点A1被映射到相集上的点A2。根据轨迹趋势,点A2一定落在点A的右侧,于是有
,且点A2是点A的后继点,则点A的后继函数为
。从点B出发的轨迹交脉冲集M于点B1,然后经过脉冲效应点B1被映射到相集上的点B2。根据轨迹趋势,点B2一定落在点B的左侧,于是有
,且点B2是点B的后继点,则点B的后继函数为
。根据解的存在唯一性定理,在A和B之间一定存在一个点Q使得
。因此,从点Q开始的轨迹
和相应的脉冲线
构成系统(2.2)的一个阶一周期解。
接下来,我们考虑阶一周期解的唯一性。在线段AB上任意取两个点
,
,使点I,J满足
。于是从点I出发的轨迹交脉冲集M于点I1,然后经过脉冲效应被映射到点I2,则点I2是点I的后继点。根据轨迹趋势可知,
。同理,从点J出发的轨迹交脉冲集M于点J1,然后经过脉冲效应被映射到点J2,则点J2是点J的后继点。根据轨迹趋势可知,
。由于
,则
。于是点I,J的后继函数满足:
.
这表明后继函数
在线段AB上是单调递减的。因此,在线段AB上仅存在一个点Q使得
,从而系统(2.2)的阶1周期解是唯一的。
情况2.
当
时,直线
在平衡点
的上方,直线
在平衡点
的下方,直线
与水平等倾线
相交,设其交点为
,并设通过点C的轨迹为LC,设直线
与轨线LC的负延长线的交点为
,且C0是直线
上距离点C最近的点,从C0到C的轨线段记为
,记由轨线段
、直线
和两坐标轴围成的区域为
(如图3),我们得到如下结论。
定理4若
为焦点且
时,则存在一个参数
满足:
当
时,系统(2.2)不存在阶一周期解,且所有的轨迹都将趋于平衡点E;
当
时,系统(2.2)存在一个唯一的阶一周期解。
证明:首先证明
的存在性。
我们知道直线
与水平等倾线
相交于点
,且通过点C的轨迹为LC,过点C做一条垂直于x轴的直线
,则直线
与轨迹LC相交,设其交点为
,其中C1是直线
上距离点C最近的点。我们再过点C1做直线
。由于函数
关于
是单调的,则这里一定存在一个参数
使得
。于是,当
时,从点C1出发的轨迹交脉冲集M于点C,且经过脉冲效应后,点C被映射到点C1。因此,轨迹
和线段
构成了系统(2.2)的一个阶一周期解,其中轨线
表示点C1和点C之间的部分。
当
时,直线
落在直线
的上方,则从某一点出发的轨迹经过有限次脉冲效应将落在轨线
的左侧,并最终趋向于平衡点E。因此,当
时,系统(2.2)不存在阶一周期解(如图3所示)。
当
时,直线
落在直线
的下方。因为直线
与直线
相交,我们将其交点表示为
(如图4所示)。根据轨迹趋势,从点
出发的轨迹一定与脉冲集M相交,且交点一定落在点C的右侧,则从点C2出发的轨迹交脉冲集M于点
,根据轨迹趋势,交点C3一定落在点C的右侧。经过脉冲效应点C3被映射到相集上的点
,则点C4是点C2的后继点,且
,于是点C2的后继函数为
。已知直线
与垂直等倾线
交于点
,则从点B出发的轨迹与脉冲集M交于点B1,然后经过脉冲效应点B1被映射到点B2,由轨迹趋势可知点B2一定落在点B的左侧,于是有
,则点B的后继函数为
。
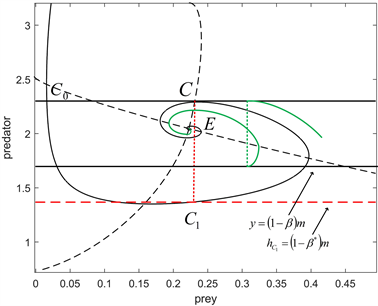
Figure 3. Existence of
and trajectory tendency for
,
图3.
的存在性及
,
时的轨线趋势
因此,由解的存在唯一性定理可知,在点C2和B之间一定存在一个点Q,使得
,即从点Q开始的轨迹
和相应的脉冲线
构成系统(2.2)的一个阶1周期解。系统(2.2)的阶1周期解的唯一性的证明方法类似于定理3。
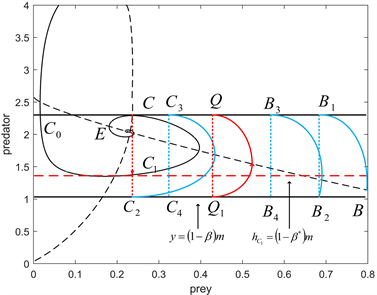
Figure 4. The order-1 periodic solution for
,
图4.
,
时的阶一周期解
4. 数值分析和生物学意义
我们选择了
为参数,分情况对系统(2.2)的阶一周期解的存在性进行了数值模拟。令
,通过数值计算,得到点
是一个焦点,其中
。
令
,此时
,根据定理3,出现阶一周期解。如图5,我们可以看到系统(2.2)在点
处存在一个阶一周期解。
令
,此时
。如图6所示,当
时在点
处存在一个阶一周期解;当
时,如图7所示,从初始点
开始的轨迹趋向于平衡点
。当
时,如图8所示,此时在点
处有一个阶一周期解。以上这些都表明数值理论结果与定理4是一致的。
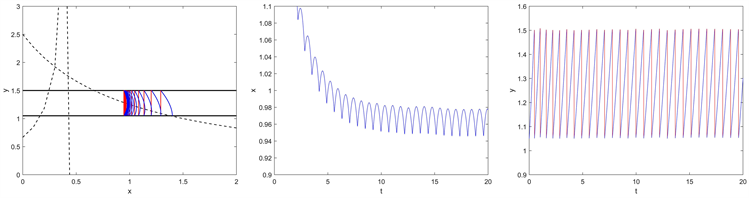
Figure 5. Phase portrait and time series of system (2.2) for
图5.
时系统(2.2)的相图和时间序列图
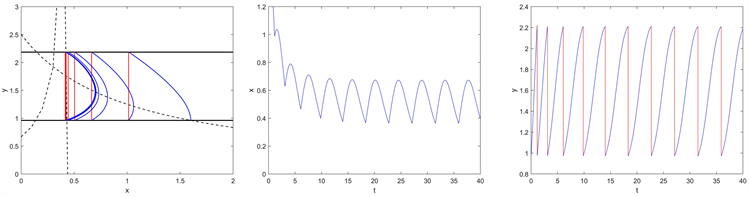
Figure 6. Phase portrait and time series of system (2.2) for
,
图6.
,
时系统(2.2)的相图和时间序列图
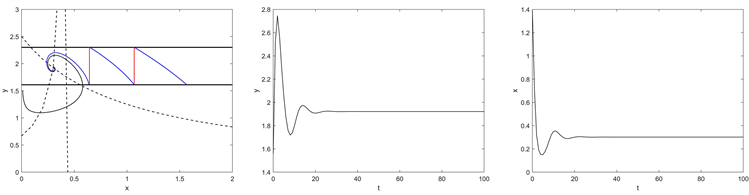
Figure 7. Phase portrait and time series of system (2.2) for
,
图7.
,
时系统(2.2)的相图和时间序列图

Figure 8. Phase portrait and time series of system (2.2) for
,
图8.
,
时系统(2.2)的相图和时间序列图
根据数值模拟,我们得到如下结论。对于自由发展系统(2.1),存在一个稳定的正平衡点
,其中
,
。当食饵的常数投放率u增大时,平衡点
会向左上方移动(如图9所示)。这说明常量投放鱼苗会更多的消耗水体的浮游动植物,有助于预防水华的发生;与此同时,常量投放一些鱼苗还会补充受水污染影响而死亡的鱼类数量,从而达到一定的产鱼量。
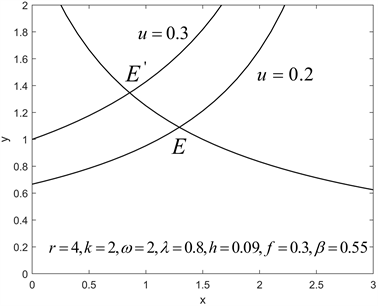
Figure 9. Relationship between equilibrium E and constant release rate u
图9. 平衡点E与常数投放率u之间的关系
以上数值模拟表明,具有脉冲状态反馈控制且捕食种群具有常数投放率的食饵捕食系统能够形成阶一周期解,且周期解是轨道渐进稳定的。这说明在一定的条件下,污染水体中的食饵和捕食种群数量能够呈周期性的震荡,且最终能够控制在适当的范围内。因此理论上只要给出合适的阈值水平,就可以通过捕食种群的常数投放率u来控制食饵捕食种群的数量,从而保持水生生态系统的平衡与稳定。
此外,如果考虑节约资源和控制投放成本,我们还提出了一个对捕食种群进行脉冲投放的生物经济模型,这将是下面的研究工作。
NOTES
*通讯作者。