曲面上的分支组合Calabi流

Branched Combinatorial Calabi Flows on Surfaces

摘要: 受蓝师义和戴道清关于分支组合Ricci流的研究启发，我们将组合Calabi流与分支结构结合，引入三角剖分曲面上的分支组合Calabi流。进一步地，我们利用分支组合Ricci势，组合Calabi能量等工具，在二维欧氏空间E²和二维双曲空间H²中，证明分支组合Calabi流的解长时间存在并且指数收敛到一个分支圆包装度量。我们的工作将葛化彬等人关于组合Calabi流的结果推广到了分支组合Calabi流情形。

Abstract: Inspired by the study of the branched combinatorial Ricci flows by Shiyi Lan and Daoqing Dai, we introduce the branched combinatorial Calabi flows on a fixed triangulated surface by combining the branch structure with the combinatorial Calabi flows. Furthermore, in 2 dimensional Euclidean space E² and 2 dimensional hyperbolic space H² , using the branched combinatorial Ricci poten-tial and combinatorial Calabi energy etc., we prove that the solutions to the branched combinatorial Calabi flows exist for the long time and converge exponentially to branched circle packing metrics. Our work extends results on the combinatorial Calabi flows by Huabin Ge et al. to the branched combinatorial Calabi flows.

1. 引言

圆包装(circle packing)理论是近几十年来在复分析和离散几何交叉学科中一个快速发展的研究领域。Thurston [1] 在1985年首次提出利用圆包装来逼近Riemann映射的猜想。Rodin和Sullivan [2] 证明了六边形情形下的Thurston猜想。此后，Beardon和Stephenson [3] 提出圆包装可用于构造离散解析函数以及将复分析的经典结果离散化的想法。分支圆包装(branched circle packing)的概念由Bowers和Stephenson [4] 提出，他们将Andreev-Thurston定理推广到了分支圆包装情形。Dubejko [5] 对分支圆包装进行了更加系统的研究，得到了曲面上分支圆包装存在的充要条件。

受Hamilton引入的Ricci流启发，Chow和罗锋 [6] 首次引进了组合Ricci流的概念，并且用其给出了Andreev-Thurston定理的新证明。此后，各种组合曲率流(包括组合Calabi流，组合Yamabe流等)相继被引入 [7] - [13]，特别地，葛化彬在博士论文 [8] 中引入了组合Calabi流，并且证明了在二维欧氏空间 ${\mathbb{E}}^2$ (2 dimensional Euclidean space)和二维双曲空间 ${ℍ}^2$ (2 dimensional hyperbolic space)中组合Calabi流解的长时间存在性及指数收敛性 [8] [9] [10] [11]。圆包装、组合曲率流可以与计算机编程结合起来，具有广泛的应用价值，例如德国的Bobenko团队 [14] 利用圆包装构造3维空间中的离散极小曲面，顾险峰团队 [15] 成功地把组合曲率流应用到计算机图形学、医学成像等领域。

基于Chow和罗锋的组合Ricci流，蓝师义和戴道清 [16] 引入了分支结构(branch structure)，提出了分支组合Ricci流，并且将Chow和罗锋的经典结果推广到了分支组合Ricci流情形。受蓝师义和戴道清 [16] 工作的启发，本文将引入分支组合Calabi流，并且尝试将葛化彬 [8] [9]，葛化彬和华波波 [10] 以及葛化彬和徐旭 [11] 等关于组合Calabi流的经典研究结果推广到分支组合Calabi流情形。

本文结构如下：第二章是预备知识。第三章讨论离散拉普拉斯算子的性质。第四章给出分支组合Calabi流解的长时间存在性证明。第五章证明分支组合Calabi流解的收敛性。

2. 预备知识

2.1. 分支圆包装

设X是一个带边或无边的紧致曲面，T是曲面X的一个三角剖分。设 $V=V\left(T\right)$， $bd\left(T\right)$， $int\left(T\right)$， $E=\left\{e_{ij}\right\}$ 和 $F=\left\{{\Delta }_{ijk}\right\}$ 分别表示T的顶点集，边界点集，内点集，边集以及面集。三角剖分的权重是一个作用于边集E上的函数 $\Phi :E\to \left[0,\frac{\pi }{2}\right]$。我们称 $\left(T,\Phi \right)$ 是曲面X的一个加权三角剖分，记加权三角剖分曲面为 $\left(X,T,\Phi \right)$。

设P是常曲率曲面上圆的一个集合，若P满足下述条件，则称之为实现加权三角剖分 $\left(T,\Phi \right)$ 的圆包装。

V中的点v与P中的圆 $C_P\left(v\right)$ 存在一一映射并且圆 $C_P\left(u\right)$ 和 $C_P\left(v\right)$ 的交角为 $\Phi =\left(e_{uv}\right)$ ；

P保持定向，即若 $v_1$， $v_2$， $v_3$ 为T中的面 ${\Delta }_{ijk}$ 按照T的定向排列的三个顶点，则 $C_P\left(v_1\right)$， $C_P\left(v_2\right)$， $C_P\left(v_3\right)$ 在曲面上形成一个正向的三圆组。

下面图1和图2是两个圆包装示例(详细信息请参见 [4])。图1和图2中均有一个固定的点v被固定在北极点(阴影圆的圆心)，就是面向读者的那个点。图1是一个外切圆包装，其中所有权重 $\Phi$ 均为0。图2和图1具有相同的加权三角剖分，但很明显相较于图1，图2更加复杂：图2依旧是外切圆包装，但是它具有两个分支点，分别在北极点和南极点(在球的背面与北极点相对)。沿着阴影圆的外切圆可以发现阴影圆的外切圆共环绕了阴影圆两周，这个圆包装诱导了球面的一个二重覆盖。

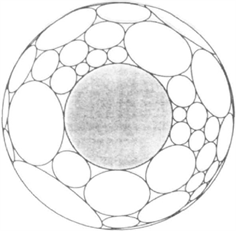
Figure 1. Circle packing with weight = 0

图1. 权重均为0的圆包装

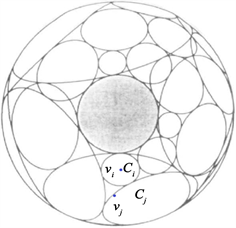
Figure 2. Branched circle packing with weight = 0

图2. 权重均为0的分支圆包装

为了更好理解分支圆包装，我们引入圆包装的半径函数概念。若P是实现加权三角剖分 $\left(T,\Phi \right)$ 的一个圆包装，则称给P中的每一个圆 $C_P\left(v\right)$ 的圆心v赋值的半径函数 $r:V\to \left(0,+\infty \right)$ 为P的圆包装度量。显然，圆包装度量 $r=\left(r_1,r_2,\cdots ,r_N\right)$ 可看作一个N维的向量，其中 $N=\left|V\right|$ 是顶点的个数。每一个内点 $v\in int\left(T\right)$ 的内角和 ${\theta }_v\left(r\right)$ 由圆包装度量决定，说明如下。记点v处的内角和 ${\theta }_v\left(r\right)={\displaystyle \sum {\alpha }_v\left(r,\Delta \right)}$，其中求和包括所有含有点v的面且 ${\alpha }_v\left(r,\Delta \right)={\alpha }_v\left(r,{\Delta }_{v{u}_1{u}_2}\right)$ 指点v， $u_1$ 和 $u_2$ 构成的三角形 ${\Delta }_{v{u}_1{u}_2}$ 中点v处的内角。

显然，由圆包装度量的定义可得，任取内点 $v\in int\left(T\right)$，它在圆包装P中的内角和一定为 $2\pi$ 的整数倍。若在圆包装P中某个内点u处的内角和等于 $2n\pi$， $n\ge 2$，那么我们称u为P中分支度为 $n-1$ 的分支点。若一个圆包装中存在至少一个分支点，则我们称该圆包装为分支圆包装。显然，图2中的南北极点都是P中分支度为1的分支点。

取一固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，考虑作用于边集E上的边长函数为 $l:E\to \left(0,+\infty \right)$。若对于任意三角形 ${\Delta }_{ijk}\in F$，三条边长 $l_{ij},l_{jk},l_{ik}$ 都满足三角不等式，则称l为一个分片线性度量。Thurston (见引理13.7.2 [1])指出，任意一个圆包装度量r都可以如下方式决定分片线性度量l。在 ${\mathbb{E}}^2$ 中，令

$l_{ij}=\sqrt{r_i^2+r_j^2+2r_i{r}_j\cos \left(\Phi \left(e_{ij}\right)\right)},$

在 ${ℍ}^2$ 中，令

$l_{ij}={\cosh }^{-1}\left(\cosh r_i\cosh r_j+\sinh r_i\sinh r_j\cos \left(\Phi \left(e_{ij}\right)\right)\right).$

记点 $v_i$ 处的内角和为 $\theta \left(v_i\right)$，则 $v_i$ 处的组合高斯曲率定义为

$K_i=2\pi -\theta \left(v_i\right),$ (1)

令 $K=\left(K_1,K_2,\cdots ,K_N\right)$。

定义2.1取一固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，若点 $\left\{b_j|j=1,\cdots ,m\right\}$ 满足 $\theta \left(b_j\right)=\left(1+{\beta }_j\right)2\pi$，且任取 $v\in int\left(T\right)\backslash \left\{b_1,b_2,\cdots ,b_m\right\}$，均有 $\theta \left(v\right)=2\pi$，则称 $b_j$ 是一个分支度为 ${\beta }_j$ 的分支点。记所有分支点为 $\left\{b_j|j=1,\cdots ,m\right\}$，且其对应的分支度分别为 ${\beta }_1,\cdots ,{\beta }_m$，则记P的分支集为

$br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\},$

称P为实现三角剖分 $\left(T,\Phi \right)$ 且具有分支集 $br\left(P\right)$ 的分支圆包装。设圆包装P实现三角剖分 $\left(T,\Phi \right)$，若存在一圆包装度量 $r:V\to \left(0,+\infty \right)$ 满足在任一点 $v_i$ 处组合高斯曲率(1)均满足下述等式

$K_i\left(r\right)+2{\beta }_i\pi =0,$ (2)

则称该圆包装度量为分支圆包装度量，且记为 $r_b$。

为简化计算，若内点 $v_i$ 不是分支点，可认为它是一个分支度为0的分支点。

定义2.2分支集 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$ 若满足下述条件，则称 $br\left(P\right)$ 是一个分支结构(branch structure)：存在一个包含至少一个内点的简单闭路径 $\Gamma =\left\{e_1,e_2,\cdots ,e_n\right\}$ 满足不等式

${\displaystyle {\sum }_{j=1}^n\left[\pi -\Phi \left(e_j\right)\right]}>2\left(l\left(\Gamma \right)+1\right)\pi ,$

这里 $l\left(\Gamma \right)={\displaystyle {\sum }_{i=1}^m{\delta }_i\left(\Gamma \right){\beta }_i}$ 且若 $\Gamma$ 包含点 $b_i$，则 ${\delta }_i=1$，否则 ${\delta }_i=0$。

Dubejko [5] 证明了当且仅当 $br\left(P\right)$ 是加权三角剖分 $\left(T,\Phi \right)$ 的一个分支结构时，实现加权三角剖分 $\left(T,\Phi \right)$ 的分支圆包装存在。

2.2. 分支组合Calabi流

在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，Chow-罗锋 [6] 首次提出的组合Ricci流方程分别如下：

$\frac{\text{d}{r}_i}{\text{d}t}=-K_i{r}_i,$ (3)

$\frac{\text{d}{r}_i}{\text{d}t}=-K_i\sinh \left(r_i\right).$ (4)

Chow-罗锋证明了组合Ricci流的解长时间存在并以指数速度收敛。在Chow-罗锋研究的基础上，蓝师义和戴道清引入分支结构，提出了分支组合Ricci流，并将Chow-罗锋的结果成功推广至分支情形。在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中的分支组合Ricci流方程分别如下：

$\frac{\text{d}{r}_i}{\text{d}t}=-\left(K_i+2{\beta }_i\pi \right)r_i,$ (5)

$\frac{\text{d}{r}_i}{\text{d}t}=-\left(K_i+2{\beta }_i\pi \right)\sinh r_i.$ (6)

葛化彬 [8] [9] 提出了组合Calabi流的概念，给出 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中的组合Calabi流方程分别如下：

$\frac{\text{d}{r}_i}{\text{d}t}=\Delta K_i{r}_i,$ (7)

$\frac{\text{d}{r}_i}{\text{d}t}=\Delta K_i\sinh r_i,$ (8)

这里 $\Delta$ 是离散拉普拉斯算子。

受蓝师义和戴道清的分支组合Ricci流启发，可定义分支组合Calabi流。

定义2.3取一固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$，则 ${\mathbb{E}}^2$ 中分支组合Calabi流定义为

$\frac{\text{d}{r}_i}{\text{d}t}=\Delta \left(K_i+2{\beta }_i\pi \right)r_i,$ (9)

${ℍ}^2$ 中的分支组合Calabi流为

$\frac{\text{d}{r}_i}{\text{d}t}=\Delta \left(K_i+2{\beta }_i\pi \right)\sinh r_i.$ (10)

当不含分支点即任意 ${\beta }_i=0$ 时，则方程(9)和(10)为葛化彬提出的组合Calabi流(7)和(8)。

2.3. 主要结果

下面是本文的主要结果，在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，我们成功将葛化彬等人的结果 [8] [11] 推广至分支情形下，得到了分支组合Calabi流解的长时间存在性与收敛性。

定理2.4.在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$，任取初值 $r\left(0\right)=\left(r_1\left(0\right),\cdots ,r_N\left(0\right)\right)\in {ℝ}_{>0}^N$ 满足 ${\displaystyle {\prod }_{i=1}^N{r}_i\left(0\right)}=1$，分支组合Calabi流(9)和(10)的解 $\left\{r\left(t\right)\right\}$ 长时间存在，且当且仅当分支圆包装度量 $r_b$ 存在时，解 $\left\{r\left(t\right)\right\}$ 收敛。若解收敛，则必指数收敛。

3. 离散拉普拉斯算子

在 ${\mathbb{E}}^2$ 中，令 $u_i=\ln r_i$，在 ${ℍ}^2$ 中，令 $u_i=\ln \tanh r_i/2$，则分支组合Calabi流方程(9)，(10)可统一写为

$\frac{\text{d}{u}_i}{\text{d}t}=\Delta \left(K_i+2{\beta }_i\pi \right).$ (11)

若点 $v_i$ 与 $v_j$ 相邻，则记作 $i~j$，因此任意边 $e_{ij}$ 均可表示为 $i~j$。在 ${\mathbb{E}}^2$ 中，对任意边 $i~j$，设

$B_{ij}=\underset{\Delta {△}_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial {\theta }_i^{jk}}{\partial r_j}{r}_j,$ (12)

在 ${ℍ}^2$ 中，对任意边 $i~j$，设

$B_{ij}=\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial {\theta }_i^{jk}}{\partial r_j}\sinh r_j,$ (13)

$A_i=\sinh r_i\frac{\partial }{\partial r_i}\left(\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}Area\left({\Delta }_{ijk}\right)\right),$ (14)

这里 ${\theta }_i^{jk}$ 是三角形 ${\Delta }_{ijk}$ 中点 $v_i$ 处的内角， $Area\left({\Delta }_{ijk}\right)$ 为三角形 ${\Delta }_{ijk}$ 的面积， $v_k$ 和 $v_l$ 是两个顶点且三角形 ${\Delta }_{ijk}$ 和 ${\Delta }_{ijl}$ 具有公共边 $e_{ij}$。

事实上，在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，均有 $B_{ij}=B_{ji}$ 成立，因为 $\frac{\partial {\theta }_i^{jk}}{\partial r_j}{r}_j=\frac{\partial {\theta }_j^{ik}}{\partial r_i}{r}_i$ 以及 $\frac{\partial {\theta }_i^{jk}}{\partial r_j}\sinh r_j=\frac{\partial {\theta }_j^{ik}}{\partial r_i}\sinh r_i$ (见 [6] 中引理2.3)。设 $A=diag\left\{A_1,A_2,\cdots ,A_N\right\}$，定义 $L_B={\left({\left(L_B\right)}_{ij}\right)}_{N\times N}$ 如下：

${\left(L_B\right)}_{ij}=\{\begin{array}{l}{\displaystyle {\sum }_{k\sim i}{B}_{ik}},i=j\\ -B_{ij},i~j\\ 0,其他\end{array}$ (15)

记 $K\left(r\right)+2\beta \pi$ 的雅可比矩阵为L，由于 $L=\left(L_{ij}\right)=\left(\frac{\partial \left(K_i+2{\beta }_i\pi \right)}{\partial u_j}\right)=\left(\frac{\partial K_i}{\partial u_j}\right)$，由 [9] 中引理3.3可得下述引理。

引理3.1在 ${ℍ}^2$ 中，L正定；在 ${\mathbb{E}}^2$ 中，L是一个 $N\times N$ 维的半正定矩阵，它的秩为 $N-1$。此外，L的零空间为 $Ker\left(L\right)=\left\{t{\left(1,\cdots ,1\right)}^{\text{T}}|t\in ℝ\right\}$。

葛化彬在 [11] 中指出在 ${\mathbb{E}}^2$ 中， $L=L_B$，在 ${ℍ}^2$ 中， $L=L_B+A$，此外， $L_B$ 半正定，A是正定的。

设f是作用在顶点集V上的任意函数，它可看作一个N维向量，则离散拉普拉斯算子Δ定义为

$\Delta f_i={\left(\Delta f\right)}_i=-{\left(L^{\text{T}}f\right)}_i=\underset{j=1}{\overset{N}{{\displaystyle \sum }}}\frac{\partial \left(K_i+2{\beta }_i\pi \right)}{\partial u_j}{f}_j.$ (16)

葛化彬在 [9] 中指出，在 ${\mathbb{E}}^2$ 中，

$\Delta f_i=\underset{j~i}{{\displaystyle \sum }}{B}_{ij}\left(f_j-f_i\right),$ (17)

此外，葛化彬和徐旭在 [11] 中指出，在 ${ℍ}^2$ 中，

$\Delta f_i=\underset{j~i}{{\displaystyle \sum }}{B}_{ij}\left(f_j-f_i\right)-A_i{f}_i.$ (18)

3.1. 对离散拉普拉斯算子的估计

这里对 $B_{ij}$ 和 $A_i$ 进行估计，我们得到下述引理。

引理3.2参考引理3.1 [11] 和引理3.1 [9] 在 ${\mathbb{E}}^2$ 中，任取 $e_{ij}$，其中 $1\le i,j\le N$，可得

$0<B_{ij}<2\sqrt{3},$ (19)

在 ${ℍ}^2$ 中，可得

$0<B_{ij}<1,$

$0<A_i<d_i\cosh 1\le d\cosh 1,$

这里 $d={\max }_{1\le i\le N}\left\{d_i\right\}$， $d_i$ 是点 $v_i$ 的度，即与 $v_i$ 相邻的点的个数。

此外，葛化彬在 [10] 中给出的引理2.2和2.3是证明方程解的长时间存在性和收敛性的关键步骤，我们可推广他的结果，得到下述两个引理。

引理3.3在 ${ℍ}^2$ 中，给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$。任选双曲三角形 ${\Delta }_{ijk}$，其三个顶点处圆的半径分别为 $r_i,r_j,r_k$，对于任意常数 $c_1\ge 1$，均存在一个充分大的常数 $C=C\left(c_1\right)>0$ 使得当 $r_i\ge C$ 时，有

$\frac{\partial }{\partial r_i}\left[\left(1+c_1\right)Area\left({\Delta }_{ijk}\right)+c_1{\theta }_i^{jk}\right]\ge 0.$

基于引理3.3，我们可以得到下述引理。

引理3.4对于任意常数 $c_1\ge 1$，均存在一个充分大的常数 $C=C\left(c_1\right)>0$ 使得当 $r_i\ge C$ 时，有

$A_i\ge c_1\underset{j\sim i}{{\displaystyle \sum }}{B}_{ij}.$

令 $c_1=1$，则引理3.3和3.4即为葛化彬 [10] 中的引理2.2和2.3。因此，我们的结果将 [10] 中引理2.2和2.3从 $c_1=1$ 推广至任意常数 $c_1\ge 1$。

下面我们将给出上述两个引理的证明。

证明[引理3.3]：取一点 ${\bar{v}}_i$，使得 ${\bar{r}}_i$ 与 $r_i$ 充分接近， ${\bar{r}}_i>r_i$ 且点 ${\bar{v}}_i$ 与点 $v_i$ 位于边 $e_{ij}$ 的同侧。在 [11] 中，葛化彬指出当圆包装度量 $r_i$ 增加时，对应点 $v_i$ 的内角 ${\theta }_i$ 会增加，显然 ${\theta }_j^{\bar{i}k}>{\theta }_j^{ik}$，所以点 $v_i$ 处于双曲三角形 ${\Delta }_{\bar{i}jk}$ 的内部，过点 $v_i$ 作 $v_{i}S\perp e_{\bar{i}j}$，垂足为点S，详情可参考图3。

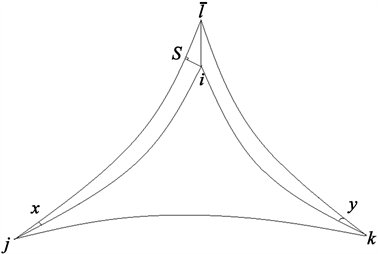
Figure 3. A hyperbolic triangle for lemma 3.3

图3. 引理3.3的一个双曲三角形

证明该引理等价于证明对于任意 ${\bar{r}}_i>r_i$，下述不等式成立。

$\left(1+c_1\right)Area\left({\Delta }_{\bar{i}jk}\right)+c_1{\theta }_{\bar{i}}^{jk}-\left(1+c_1\right)Area\left({\Delta }_{ijk}\right)-c_1{\theta }_i^{jk}\ge 0.$

由 ${ℍ}^2$ 中的Gauss-Bonnet公式得，在双曲三角形 ${\Delta }_{ijk}$ 中有 ${\theta }_i^{jk}+{\theta }_j^{ik}+{\theta }_k^{ij}=\pi -Area\left({\Delta }_{ijk}\right)$。

设 $x={\theta }_j^{\bar{i}k}-{\theta }_j^{ik}$， $y={\theta }_k^{\bar{i}j}-{\theta }_k^{ij}$，可得

$\begin{array}{l}\left(1+c_1\right)Area\left({\Delta }_{\bar{i}jk}\right)+c_1{\theta }_{\bar{i}}^{jk}-\left(1+c_1\right)Area\left({\Delta }_{ijk}\right)-c_1{\theta }_i^{jk}\\ =Area\left({\Delta }_{\bar{i}jk}\right)-Area\left({\Delta }_{ijk}\right)-c_{1}x-c_{1}y\\ =Area\left({\Delta }_{\bar{i}ij}\right)+Area\left({\Delta }_{\bar{i}ik}\right)-c_{1}x-c_{1}y\\ =Area\left({\Delta }_{\bar{i}ij}\right)-c_{1}x+Area\left({\Delta }_{\bar{i}ik}\right)-c_{1}y.\end{array}$ (20)

所以我们仅需证明 $Area\left({△}_{\bar{i}ij}\right)-c_{1}x\ge 0$ 即可。由于 ${\bar{r}}_i>r_i$，可得 $l_{\bar{i}j}>l_{ij}$， ${\theta }_i^{\bar{i}j}>{\theta }_{\bar{i}}^{ij}$。考虑到 ${\theta }_i^{\bar{i}j}+{\theta }_{\bar{i}}^{ij}+x=\pi -Area\left({\Delta }_{\bar{i}ij}\right)<\pi$，因此 ${\theta }_{\bar{i}}^{ij}<\frac{\pi }{2}$。由于 ${\bar{r}}_i$ 充分接近于 $r_i$，所以 $l_{\bar{i}i}\le 1$。由双曲余弦定理得 $\cos x$ 的极限存在，即

$\cos x=\frac{\cosh l_{ij}\cosh l_{\bar{i}j}-\cosh l_{\bar{i}i}}{\sinh l_{ij}\sinh l_{\bar{i}j}}\to 1,r_i\to +\infty .$

因此可以找到一个正常数 $C_1$ 使得当 $r_i\ge C_1$ 时，有 $x\le \frac{\pi }{4\left(1+c_1\right)}$ 成立。

设 $\gamma ={\theta }_{v_i}^{S{v}_j}$，当 $\gamma <\frac{\pi }{4}$ 时，显然有 $\gamma +\left(1+c_1\right)x<\frac{\pi }{2}$，然而由 ${ℍ}^2$ 中的Gauss-Bonnet公式得

$\gamma +x+\frac{\pi }{2}+Area\left({\Delta }_{S{v}_i{v}_j}\right)=\pi ,$

因此 $Area\left({\Delta }_{\bar{i}ij}\right)>Area\left({\Delta }_{S{v}_i{v}_j}\right)>c_{1}x$。

当 $\gamma \ge \frac{\pi }{4}$ 时， $\frac{\sinh l_{S{v}_j}}{\sinh l_{ij}}=\sin \gamma \ge \frac{\sqrt{2}}{2}$。由于 $\cos \gamma =\sin x\cosh l_{S{v}_j}$， $\cos x=\frac{\tanh l_{S{v}_j}}{\tanh l_{ij}}$ 并且 $\sin \sin \gamma =\frac{\sinh l_{S{v}_j}}{\sinh l_{ij}}$，然后由 [10] 得

$\sin \left(Area\left({\Delta }_{S{v}_i{v}_j}\right)\right)\ge \sin x\frac{\cosh r_i-1}{\sqrt{2}}.$ (21)

考虑到当 $x>0$ 时， $\cosh x$ 递增且无上界，因此这里我们可以选取一个常数 $C_2$ 使得当 $r_i\ge C_2$ 时有 $\frac{\cosh r_i-1}{\sqrt{2}}\ge c_1$。因此可得

$\sin \left(Area\left({\Delta }_{S{v}_i{v}_j}\right)\right)\ge c_1\sin x\ge \sin c_{1}x,$

因为x和 $c_{1}x$ 都属于 $\left(0,\frac{\pi }{2}\right)$ 且 $c_1\ge 1$，所以右侧不等式成立。注意到 $Area\left({\Delta }_{S{v}_i{v}_j}\right)\in \left(0,\frac{\pi }{2}\right)$，因此可得

$Area\left({\Delta }_{\bar{i}ij}\right)>Area\left({\Delta }_{S{v}_i{v}_j}\right)>c_{1}x,$

记 $C=\max \left\{C_1,C_2\right\}$，则引理3.3证毕。

下面我们将证明引理3.4。

证明[引理3.4]：

$\begin{array}{c}{A}_i-c_1\underset{j~i}{{\displaystyle \sum }}{B}_{ij}=\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial Area\left({\Delta }_{ijk}\right)}{\partial r_i}\sinh r_i-c_1\underset{j~i}{{\displaystyle \sum }}\left(\frac{\partial {\theta }_i^{jk}}{\partial r_j}\sinh r_j+\frac{\partial {\theta }_i^{jl}}{\partial r_j}\sinh r_j\right)\\ =\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial Area\left({\Delta }_{ijk}\right)}{\partial r_i}\sinh r_i-c_1\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\left(\frac{\partial {\theta }_j^{ik}}{\partial r_i}\sinh r_i+\frac{\partial {\theta }_k^{ij}}{\partial r_i}\sinh r_i\right)\\ =\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial \left(Area\left({\Delta }_{ijk}\right)-c_1{\theta }_j^{ik}-c_1{\theta }_k^{ij}\right)}{\partial r_i}\sinh r_i\\ =\underset{{\Delta }_{ijk}\in F}{{\displaystyle \sum }}\frac{\partial \left[\left(1+c_1\right)Area\left({\Delta }_{ijk}\right)+c_1{\theta }_i^{jk}\right]}{\partial r_i}\sinh r_i\ge 0.\end{array}$ (22)

证毕。

定义3.5在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$，定义分支组合Calabi能量E为

$E\left(r\right)=\underset{i=1}{\overset{N}{{\displaystyle \sum }}}\left(K_i\left(r\right)+2{\beta }_i\pi \right).$ (23)

3.2. 分支组合Ricci势

在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，因为 $\frac{\partial \left(K_i+2{\beta }_i\pi \right)}{\partial u_j}=\frac{\partial \left(K_j+2{\beta }_j\pi \right)}{\partial u_i}$ (参考引理2.3 [6])，所以光滑1-形式 ${\displaystyle {\sum }_{i=1}^N\left(K_i\left(u\right)+2{\beta }_i\pi \right)\text{d}{u}_i}$ 是闭的。蓝师义–戴道清 [16] 定义分支组合Ricci势如下。

定义3.6给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$。在 ${\mathbb{E}}^2$ 中，定义分支组合Ricci势为：

$F\left(u\right)={\displaystyle {\int }_a^u\underset{i=1}{\overset{N}{{\displaystyle \sum }}}}\left(K_i\left(u\right)+2{\beta }_i\pi \right)\text{d}{u}_i,u\in {ℝ}^N,$ (24)

在 ${ℍ}^2$ 中，定义分支组合Ricci势为

$F\left(u\right)={\displaystyle {\int }_a^u\underset{i=1}{\overset{N}{{\displaystyle \sum }}}}\left(K_i\left(u\right)+2{\beta }_i\pi \right)\text{d}{u}_i,u\in {ℝ}_{<0}^N,$ (25)

这里 $a\in {ℝ}^N$ 是任意常数。

引理3.7在 ${\mathbb{E}}^2$ 中，若分支组合Calabi流方程的解 $\left\{r\left(t\right)\right\}$ 存在，则 ${\displaystyle {\prod }_{i=1}^N{r}_i\left(t\right)}={\displaystyle {\prod }_{i=1}^N{r}_i\left(0\right)}$ 以及 ${\displaystyle {\sum }_{i=1}^N{u}_i\left(t\right)}={\displaystyle {\sum }_{i=1}^N{u}_i\left(0\right)}$ 均是常数。

由 [16] 中定理1，可得分支组合Ricci势的凸性：

引理3.8在 ${ℍ}^2$ 中，分支组合Ricci势F在 ${\left(-\infty ,0\right)}^N$ 上严格凸。在 ${\mathbb{E}}^2$ 中，F在 ${ℝ}^N$ 上凸且在超平面 $\mathcal{U}=\left\{{\left(u_1\left(t\right),u_2\left(t\right),\cdots ,u_N\left(t\right)\right)}^{\text{T}}|{\displaystyle {\sum }_{i=1}^N{u}_i\left(t\right)}=0\right\}$ (或超曲面 $\mathcal{P}=\left\{{\left(r_1\left(t\right),r_2\left(t\right),\cdots ,r_N\left(t\right)\right)}^{\text{T}}|{\displaystyle {\prod }_{i=1}^N{r}_i\left(t\right)}=1\right\}$ )上严格凸。

由引理3.8可得下述刚性定理，参考文献 [4] [5] [16]。

引理3.9在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，记圆包装度量 ${\left(r_1\left(t\right),r_2\left(t\right),\cdots ,r_N\left(t\right)\right)}^{\text{T}}$ 到组合高斯曲率 ${\left(K_1\left(t\right),K_2\left(t\right),\cdots ,K_N\left(t\right)\right)}^{\text{T}}$ 的映射为 $\Pi :{ℝ}_{>0}^N\to {ℝ}^N$。则

在 ${ℍ}^2$ 中，Π是单射，所以组合高斯曲率唯一决定圆包装度量。

在 ${\mathbb{E}}^2$ 中，在超平面 $\mathcal{U}=\left\{{\left(u_1\left(t\right),u_2\left(t\right),\cdots ,u_N\left(t\right)\right)}^{\text{T}}|{\displaystyle {\sum }_{i=1}^N{u}_i\left(t\right)}=0\right\}$ 上，Π是单射，所以在不考虑刚性运动下组合高斯曲率唯一决定圆包装度量，即K与aK决定同一圆包装度量，这里a是任意非零常数。

葛化彬(参考定理B.2 [9])和葛化彬–徐旭(参考引理B.1 [11])证明了组合Ricci势在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中的真性，这里我们可将他们的结果推广到分支情形。

引理3.10在 ${ℍ}^2$ 中，分支组合Ricci势F(25)满足

$\underset{\Vert u\Vert \to +\infty }{\lim }F\left(u\right)=+\infty ,$ (26)

在 ${\mathbb{E}}^2$ 中，分支组合Ricci势F(24)满足

$\underset{\Vert u\Vert \to +\infty }{\lim }{F\left(u\right)|}_{u\in \mathcal{U}}=+\infty .$ (27)

由于引理B.1 [11] 得 $F^{\text{*}}\left(u\right)={\displaystyle {\int }_a^u{\displaystyle {\sum }_{i=1}^N{K}_i\left(u\right)\text{d}{u}_i}}$ 满足真性，显然有引理3.10成立。

4. 分支组合Calabi流解的长时间存在性

在这章中，我们将证明在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，分支组合Calabi流的解 $\left\{r\left(t\right)\right\}$ 长时间存在。

定理4.1在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$。任给初值圆包装度量 $r\left(0\right)$，分支组合Calabi流的解 $\left\{r\left(t\right)\right\}$ 长时间存在。

为了证明该定理，我们需要下面的引理(参考引理3.5 [6])。

引理4.2对于任意的 $ϵ>0$，均存在一个充分大的常数l，使得当 $r_i>l$ 时，双曲三角形 ${\Delta }_{ijk}$ 中点 $v_i$ 处的内角 ${\theta }_i^{jk}$ 有

${\theta }_i^{jk}<ϵ.$

现在我们开始证明定理4.1。

证明：设 $d_i$ 为点 $v_i$ 处的度，即与 $v_i$ 相邻的点的个数。记 $d=\max \left\{d_1,\cdots ,d_N\right\}$，则 $\left(2-d\right)\pi <K_i<2\pi$。在 ${\mathbb{E}}^2$ 中，

$\begin{array}{c}\Delta \left(K_i+2{\beta }_i\pi \right)=-{\left[L^{\text{T}}\left(K+2\beta \pi \right)\right]}_i\\ =-\underset{j=1}{\overset{N}{{\displaystyle \sum }}}{L}_{ij}\left(K_j+2{\beta }_j\pi \right)\\ =-\underset{j\sim i}{{\displaystyle \sum }}\left(-B_{ij}\right)\left(K_j+2{\beta }_j\pi \right)-L_{ii}\left(K_i+2{\beta }_i\pi \right)\\ =\underset{j\sim i}{{\displaystyle \sum }}{B}_{ij}\left(K_j-K_i+2{\beta }_j\pi -2{\beta }_i\pi \right).\end{array}$ (28)

由引理3.2得 $0<B_{ij}<2\sqrt{3}$，可得 $\left|\Delta \left(K_i+2{\beta }_i\pi \right)\right|$ 上有界，即

$\left|\Delta \left(K_i+2{\beta }_i\pi \right)\right|<2\sqrt{3}N\left(d+2{\beta }_{\max }\right)\pi \triangleq c,$

这里 ${\beta }_{\max }=\max \left\{{\beta }_1,{\beta }_2,\cdots ,{\beta }_N\right\}$。

因此 $\left|\frac{\text{d}{u}_i}{\text{d}t}\right|<c$，进而我们得到解 $\left\{r\left(t\right)\right\}$ 满足

$c_2{\text{e}}^{-ct}\le r_i\le c_3{\text{e}}^{ct},$

这里 $c_2=\min \left\{r_1\left(0\right),r_2\left(0\right),\cdots ,r_N\left(0\right)\right\}$， $c_3=\max \left\{r_1\left(0\right),r_2\left(0\right),\cdots ,r_N\left(0\right)\right\}$，因此在 ${\mathbb{E}}^2$ 中分支组合Calabi流(9)的解 $\left\{r\left(t\right)\right\}$ 长时间存在。

在 ${ℍ}^2$ 中，根据引理4.2，可得对于任意点 $v_i$，存在一个充分大的 $l>0$，使得当 $r_i>l$ 时，三角形 ${\Delta }_{ijk}$ 中点 $v_i$ 处的内角 ${\theta }_i^{jk}$ 小于 $\frac{\pi }{d}$，因此 $K_i>\pi$。令(18)中 $f=K+2\beta \pi$，则

$\begin{array}{c}\frac{1}{\sinh r_i}\frac{\text{d}{r}_i}{\text{d}t}=\underset{j~i}{{\displaystyle \sum }}{B}_{ij}\left(K_j-K_i+2{\beta }_j\pi -2{\beta }_i\pi \right)-A_i\left(K_i+2{\beta }_i\pi \right)\\ <\underset{j~i}{{\displaystyle \sum }}{B}_{ij}\left(2\pi -K_i+2{\beta }_{\max }\pi -2{\beta }_i\pi \right)-A_i\left(K_i+2{\beta }_i\pi \right)\\ =\left(2\pi +2{\beta }_{\max }\pi \right)\underset{j~i}{{\displaystyle \sum }}{B}_{ij}-\left(\underset{j~i}{{\displaystyle \sum }}{B}_{ij}+A_i\right)\left(K_i+2{\beta }_i\pi \right)\\ \le \left(2\pi +4{\beta }_{\max }\pi \right)\underset{j~i}{{\displaystyle \sum }}{B}_{ij}-\left(\pi +2{\beta }_{\min }\pi \right)\left(\underset{j~i}{{\displaystyle \sum }}{B}_{ij}+A_i\right)\\ =\left(\pi +2{\beta }_{\min }\pi \right)\left[\frac{1+4{\beta }_{\max }-2{\beta }_{\min }}{1+2{\beta }_{\min }}\underset{j~i}{{\displaystyle \sum }}{B}_{ij}-A_i\right].\end{array}$ (29)

令引理3.4中 $c_1=\frac{1+4{\beta }_{\max }-2{\beta }_{\min }}{1+2{\beta }_{\min }}\ge 1$， $Q=\max \left\{l,C,r_i\left(0\right)+1\right\}$，则当 $r_i>Q$ 时，有 $\frac{1}{\sinh r_i}\frac{\text{d}{r}_i}{\text{d}t}<0$，所以解 $\left\{r\left(t\right)\right\}$ 有上界。

下面我们将证明解 $\left\{r\left(t\right)\right\}$ 有下界。这里我们需要考虑分支组合Ricci势 $F\left(u\right)$，对 $F\left(u\right)$ 求导得 $\frac{\text{d}F\left(u\right)}{\text{d}t}=\left(K+2\beta \pi \right)\left(-L^{\text{T}}\right)\left(K+2\beta \pi \right)\le 0$，因此 $F\left(u\right)$ 沿着分支组合Calabi流是单调不增的。又因为引理3.10指出 ${\lim }_{\Vert u\Vert \to +\infty }F\left(u\right)=+\infty$，所以存在一个仅依赖于三角剖分，分支结构与初值 $r\left(0\right)$ 的正常数 $\delta$，使得对于任意点 $v_i$ 和时间t，均有 $u_i\left(t\right)\ge -\delta$，因此解 $r_i\left(t\right)$ 有下界，即

$r_i\ge \ln \frac{1+{\text{e}}^{-\delta }}{1-{\text{e}}^{-\delta }}.$

综上，在 ${ℍ}^2$ 中分支组合Calabi流的解 $\left\{r\left(t\right)\right\}$ 长时间存在，证毕。

5. 分支组合Calabi流解的收敛性

在这一章中，我们将证明在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中分支组合Calabi流(9)和(10)解 $\left\{r\left(t\right)|t\in \left[0,+\infty \right)\right\}$ 的收敛性。

定理5.1在 ${ℍ}^2$ 和 ${\mathbb{E}}^2$ 中，给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$。任取一初值圆包装度量 $r\left(0\right)=\left(r_1\left(0\right),\cdots ,r_N\left(0\right)\right)\in {ℝ}_{>0}^N$ 满足 ${\displaystyle {\prod }_{i=1}^N{r}_i\left(t\right)}=1$，设 $\left\{r\left(t\right)|t\in \left[0,+\infty \right)\right\}$ 是分支组合Calabi流长时间存在的解，则当且仅当存在一个分支圆包装度量 $r_b$ 时，解 $\left\{r\left(t\right)\right\}$ 收敛。若解收敛，则必指数收敛。

为了证明定理5.1，我们需要下面的引理。

引理5.2在 ${\mathbb{E}}^2$ 和 ${ℍ}^2$ 中，给定一个固定的加权三角剖分曲面 $\left(X,T,\Phi \right)$，其分支结构为 $br\left(P\right)=\left\{\left(b_1,{\beta }_1\right),\left(b_2,{\beta }_2\right),\cdots ,\left(b_m,{\beta }_m\right)\right\}\subset V\times N$。设存在一个分支圆包装度量 $r_b$，分支组合Calabi流的解 $\left\{r\left(t\right)\right\}\subset M$，这里M是 ${ℝ}_{>0}^N$ 中的一紧集，则解 $\left\{r\left(t\right)\right\}$ 指数收敛到分支圆包装度量 $r_b$。

下面我们将给出引理5.2的证明。

证明：对 $K_i+2{\beta }_i\pi$ 求导，得到

$\frac{\text{d}\left(K+2\beta \pi \right)}{\text{d}t}=\frac{\text{d}\left(K+2\beta \pi \right)}{\text{d}u}\frac{\text{d}u}{\text{d}t}=-L^2\left(K+2\beta \pi \right)\text{.}$

因为L在 ${ℍ}^2$ 中是正定的，在 ${\mathbb{E}}^2$ 中半正定，所以我们可取L的最小正特征值为 ${\lambda }_1$，然后对分支组合Calabi能量进行求导得到

$\begin{array}{c}{E}^{\prime }\left(t\right)=2{\left(K+2\beta \pi \right)}^{\text{T}}{\left(K+2\beta \pi \right)}^{\prime }\\ =-2{\left(K+2\beta \pi \right)}^T{L}^2\left(K+2\beta \pi \right)\\ \le -2{\lambda }_1^2{\left(K+2\beta \pi \right)}^T\left(K+2\beta \pi \right)\\ =-2{\lambda }_1^{2}E\left(t\right).\end{array}$

因此我们得到 $E\left(t\right)\le E_0{\text{e}}^{-2{\lambda }_1^{2}t}$ 且 $\left|K_i\left(t\right)+2{\beta }_i\pi \right|\le \left|K\left(t\right)+2\beta \pi \right|=\sqrt{E\left(t\right)}\le \sqrt{E_0}{\text{e}}^{-{\lambda }_1^{2}t}$。又因为 $\left\{r\left(t\right)\right\}\subset M$，M是 ${ℝ}_{>0}^N$ 中一紧集，所以沿着分支组合Calabi流， $L_{ij}$， $r_i$ 和 $\sinh r_i$ 是有界的。因此在 ${\mathbb{E}}^2$ 中，我们有

$\left|\frac{\text{d}{r}_i}{\text{d}t}\right|=\left|r_i\Delta \left(K_i+2{\beta }_i\pi \right)\right|=\left|r_i\underset{j=1}{\overset{N}{{\displaystyle \sum }}}{L}_{ij}\left(K_j+2{\beta }_j\pi \right)\right|\le m{\text{e}}^{-{\lambda }_1^{2}t},$

在 ${ℍ}^2$ 中，可得

$\left|\frac{\text{d}{r}_i}{\text{d}t}\right|=\left|\sinh r_i\underset{j=1}{\overset{N}{{\displaystyle \sum }}}{L}_{ij}\left(K_j+2{\beta }_j\pi \right)\right|\le n{\text{e}}^{-{\lambda }_1^{2}t},$

这里 $m,n$ 是两个充分大的正常数。这说明，无论是在 ${\mathbb{E}}^2$ 还是 ${ℍ}^2$ 中，分支组合Calabi流的解 $\left\{r\left(t\right)\right\}$ 指数收敛。记 $r\left(t\right)\to r^{\text{*}},t\to +\infty$ 以及 $K\left(t\right)\to K^{\text{*}},t\to +\infty$，显然 $K^{\text{*}}+2\beta \pi =0$，所以由引理3.9得 $r^{\text{*}}$ 实际上是一个分支圆包装度量 $r_b$，证毕。

下面我们将给出定理5.1的证明。

证明：在 ${\mathbb{E}}^2$ 中，根据引理5.2的证明，容易得到，若分支组合Calabi流的解 $\left\{r\left(t\right)|t\in \left[0,+\infty \right)\right\}$ 收敛，则分支圆包装度量 $r_b$ 存在。

另一方面，假设分支圆包装度量 $r_b$ 存在，设 $\left\{r\left(t\right)|t\in \left[0,+\infty \right)\right\}$ 是分支组合Calabi流的解，令 $u_i\left(t\right)=\ln r_i\left(t\right)$，由 ${\displaystyle {\prod }_{i=1}^N{r}_i\left(0\right)}=1$ 得初值圆包装度量 $u_0$ 在超平面 $\mathcal{U}=\left\{{\left(u_1\left(t\right),u_2\left(t\right),\cdots ,u_N\left(t\right)\right)}^{\text{T}}|{\displaystyle {\sum }_{i=1}^N{u}_i\left(t\right)}=0\right\}$ 上，由引理3.7可得解 $\left\{u\left(t\right)|t\in \left[0,+\infty \right)\right\}\subset \mathcal{U}$。令分支组合Ricci势定义中的 $a=u_b$，由引理3.9得分支组合Ricci势的梯度映射 $\nabla F:u\to K+2\beta \pi$ 是单射，并且 $u=u_b$ 是F唯一的临界点。由引理3.1得F的海塞矩阵L是半正定的，所以有 $F\left(u\right)\ge F\left(u_b\right)=0$。进一步地，我们还可以得到

$\frac{\text{d}F}{\text{d}t}=\underset{i=1}{\overset{N}{{\displaystyle \sum }}}\left(K_i+2{\beta }_i\pi \right)\frac{\text{d}{u}_i}{\text{d}t}=-{\left(K+2\beta \pi \right)}^{\text{T}}{L}^{\text{T}}\left(K+\beta \pi \right)\le 0.$

所以F沿着分支组合Calabi流是单调递减的，即 $0=F\left(u_b\right)\le F\left(u\right)\le F\left(u\left(0\right)\right)$，由引理3.10，可得 ${\lim }_{\Vert u\Vert \to +\infty }{F\left(u\right)|}_{u\in \mathcal{U}}=+\infty$，因此 $\left\{u\left(t\right)\right\}\subset {\left({F|}_{u\in \mathcal{U}}\right)}^{-1}\left[0,F\left(u\left(0\right)\right)\right]$ 且 ${\left({F|}_{u\in \mathcal{U}}\right)}^{-1}\left[0,F\left(u\left(0\right)\right)\right]$ 是一个紧集，因此 $\left\{r\left(t\right)\right\}\subset M$，这里M是 ${ℝ}_{>0}^N$ 中的一紧集，所以由引理5.2，可得分支组合Calabi流方程解 $\left\{r\left(t\right)\right\}$ 指数收敛到分支圆包装度量 $r_b$。

在 ${ℍ}^2$ 中，证明与在 ${\mathbb{E}}^2$ 中完全类似，此处省略。证毕。

6. 结论

分支组合Calabi流是四阶曲率流，无法建立类似Chow和罗锋 [6] 在组合Ricci流证明中的极大原理，这是研究的一大难点。我们推广了葛化彬等人 [8] [9] [10] [11] 在组合Calabi流中使用的几何方法，克服了难点，证明了分支组合Calabi流解的长时间存在性与收敛性。

引理3.3和引理3.4中的一致估计是分支组合Calabi流解的长时间存在性与收敛性证明的关键步骤，为此我们将葛化彬和华波波 [10] 中的类似估计从 $c_1=1$ 成功推广到了任意常数 $c_1\ge 1$。

综上所述，本文对于组合曲率流的理论研究具有一定的借鉴价值，同时还有潜在的应用价值。

基金项目

国家自然科学基金面上项目(12171480)，湖南省杰出青年基金项目(2022JJ10059)，湖南省自然科学基金面上项目(2020JJ4658)资助。

NOTES

^*通讯作者。