具有垂直传染和分布时滞的SEI传染病模型

SEI Infectious Disease Model with Vertical Transmission and Distribution Time Delay

摘要: 本文以北美僵尸鹿传染病传播特征为生物背景，建立了具有垂直传染和分布时滞的SEI传染病模型。通过定义界定疾病是否传播的基本再生数R₀，分别给出了模型无病平衡点全局渐近稳定以及患病鹿群持久生存的充分条件：即当R₀ ≤ 1时，无病平衡点E0是全局渐近稳定的；当R₀ > 1时，患病鹿群是持久的。文末的数值模拟不仅验证了定性理论结果的正确性，同时展示了僵尸鹿病毒潜伏期和死亡率对鹿种群数量的影响。

Abstract: In this paper, we study an SEI infectious disease model with vertical transmission and distribution time delay that was developed using the infectious disease transmission characteristics of zombie deer in North America as the biological background. By defining the basic reproduction number that defines whether the disease is transmitted or not, sufficient conditions are given for the global asymptotic stability of the disease-free equilibrium point and the persistence of the diseased deer population, respectively: when the basic reproduction number less than or equal to one, the dis-ease-free equilibrium point is globally asymptotically stable; when the basic reproduction number greater than one, the diseased deer population is persistent. The numerical simulation at the end of the paper not only verifies the correctness of the qualitative theoretical results, but also demon-strates the effects of zombie deer virus incubation period and mortality on deer population size.

1. 引言

生物种群的生存状态始终受到学术界的广泛关注，传染病模型更是近年来生物数学领域的研究重点之一，学者们对传染病模型进行了大量的研究 [1] - [10] 。在具有常数输入率的传染病模型中，基本再生数是确定疾病流行与否的重要阈值。当基本再生数大于1时，疾病将持续存在形成地方病；当基本再生数小于1时，疾病灭绝。

僵尸鹿病又称鹿科动物慢性消耗性疾病(Chronic Wasting Disease, CWD)，是一种朊病毒病，会感染北美白尾鹿、山麋鹿、黑尾鹿和麋鹿 [11] [12] 。2018年致命的僵尸鹿病毒侵袭了北美许多州和省的鹿群，鹿群呈现出明显的“僵尸般的”症状，因此这种疾病被称为“僵尸鹿传染病”。实验研究结果表明，“僵尸鹿传染病”是由朊病毒引起的，是正常蛋白质的异常形式，可导致机体自身蛋白质异常、生理和其他异常 [13] 。CWD传染性病原体能够通过摄入感染动物的体液(例如唾液、粪便、尿液、胎盘组织)中的朊病毒传播，也可以通过接触受污染的牧场或者死亡动物的腐烂尸体传播，受CWD感染的血液中含有足够水平的朊病毒以引起疾病 [14] 。从目前的研究来看，此种疾病的传播方式主要是水平传染和垂直传染 [15] [16] [17] [18] ，由于人类食用鹿肉，所以即使没有直接的证据表明鹿朊病毒株能够感染人类，但也不能完全排除人类被僵尸鹿病毒感染的可能性，世界各地的科学家、医生和兽医在了解了僵尸鹿传染病在美国的传播情形后，加强了对僵尸鹿传染病的研究。

2. 模型的建立

2013年李冬梅和卢旸发表了一篇题为“一类具有连续接种的自治SEIR传染病模型”的文章 [19] ，本文将结合“僵尸鹿传染病”的传播特点并参考文献 [19] 的研究思想，考虑如下具有垂直传染和分布时滞的SEI传染病模型：

$\{\begin{array}{l}{S}^{\prime }\left(t\right)=\mu \left(E\left(t\right)+S\left(t\right)+pI\left(t\right)\right)-\beta S\left(t\right)I\left(t\right)-\mu S\left(t\right)\hfill \\ E^{\prime }\left(t\right)=\beta S\left(t\right)I\left(t\right)-\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)S\left(t-\xi \right)I\left(t-\xi \right)e^{-\mu \xi }\text{d}\xi }+q\mu I\left(t\right)-\mu E\left(t\right)\hfill \\ I^{\prime }\left(t\right)=\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)S\left(t-\xi \right)I\left(t-\xi \right)e^{-\mu \xi }\text{d}\xi }-\mu I\left(t\right)\hfill \end{array}$ (1)

其中 $S\left(t\right)$ 表示t时刻易感北美鹿的种群数量， $E\left(t\right)$ 表示t时刻染病后处于潜伏期的北美鹿的种群数量， $I\left(t\right)$ 表示t时刻已经患病并且表现出患病状态的北美鹿种群数量。 $\mu$ 为鹿群的出生率和死亡率； $p\mu I\left(t\right)$ 是染病鹿群在t时刻出生的新生鹿群没有被垂直感染的数量( $0<p<1$ )； $q\mu I\left(t\right)$ 是染病鹿群在t时刻出生的新生鹿群被垂直感染后直接进入到潜伏期鹿群的数量( $0<q<1$ 和 $p+q=1$ )； $\tau$ 为鹿种群感染CWD后

的最大潜伏期； $f\left(\xi \right)$ 是 $\left[0,\tau \right]$ 上的非负函数并且满足 ${\displaystyle {\int }_{\text{0}}^{\tau }f\left(\xi \right)\text{d}s}=1$， ${\displaystyle {\int }_{\text{0}}^{\tau }\xi f\left(\xi \right)\text{d}\xi }<+\infty$，模型中所有的参

数均为正数。

由模型(1)，可以得到t时刻鹿种群总数为 $N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)$，满足 $N^{\prime }\left(t\right)\equiv 0\left(t\ge 0\right)$，即鹿种群的种群总数量为常数，不失一般性，可设 $N\left(t\right)\equiv 1$。又由于模型(1)中的第三个方程不含有 $E\left(t\right)$，从而可以简化模型(1)为只含有 $S\left(t\right)$ 和 $I\left(t\right)$ 的二维方程。方程如下：

$\{\begin{array}{l}{S}^{\prime }\left(t\right)=\mu \left(1-S\left(t\right)\right)-\beta S\left(t\right)I\left(t\right)-\mu qI\left(t\right)\hfill \\ I^{\prime }\left(t\right)=\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)S\left(t-\xi \right)I\left(t-\xi \right)e^{-\mu \xi }}\text{d}\xi -\mu I\left(t\right)\hfill \end{array}$ (2)

记Banach空间C表示所有的连续映射。 $\varphi :\left[-\tau ,0\right]\to R_{+}^2$ 的范数定义为：

$\Vert \phi \Vert =\underset{-\tau \le \theta \le 0}{\sup }\left\{\left|{\varphi }_1\left(\theta \right)\right|,\left|{\varphi }_2\left(\theta \right)\right|\right\}=\left({\varphi }_1,{\varphi }_2\right).$

此外令 $C_{+}=\left\{\varphi =\left({\varphi }_1,{\varphi }_2\right)\in C:{\varphi }_i\left(\theta \right)\ge 0,\forall \theta \in \left[-\tau ,0\right],{\varphi }_i\left(\theta \right)>0\right\}$。

假设模型(2)的任意解 $\left(S\left(t\right),I\left(t\right)\right)$ 满足初始条件：

$S\left(\theta \right)={\varphi }_1\left(\theta \right),I\left(\theta \right)={\varphi }_2\left(\theta \right)\left(-\tau \le \theta \le 0\right),\left({\varphi }_1,{\varphi }_2\right)\in C_{+}.$ (3)

命题2.1 对任意的 $t\ge 0$，模型(2)具有初值条件(3)的任意解 $\left(S\left(t\right),I\left(t\right)\right)$ 存在且非负。

证明：由于模型(2)的右端是全连续的，因此模型(2)具有初值条件(3)的任意解 $\left(S\left(t\right),I\left(t\right)\right)$ 存在且唯一。此外，形式的求解模型(2)关于 $S\left(t\right)$ 过 $S\left(0\right)$ 的解和 $I\left(t\right)$ 过 $I\left(0\right)$ 的解，可得：

$\begin{array}{l}S\left(t\right)=S\left(0\right){\text{e}}^{-{\displaystyle {\int }_0^t\left(\mu +\beta I\left(\xi \right)\right)\text{d}\xi }}+\mu \left(1-qI\left(t\right)\right)\cdot {\displaystyle {\int }_0^t{\text{e}}^{-{\displaystyle {\int }_{\eta }^t\left(\mu +\beta I\left(\xi \right)\right)\text{d}\xi }}}\text{d}\eta \\ I\left(t\right)=I\left(0\right){\text{e}}^{-\mu t}+\beta {\displaystyle {\int }_0^{\tau }f\left(\zeta \right)S\left(t-\xi \right)I\left(t-\xi \right){\text{e}}^{-\mu \xi }\text{d}\xi }\cdot {\displaystyle {\int }_0^t{\text{e}}^{-\mu \left(t-\eta \right)}\text{d}\eta }\end{array}$

由于对任意的 $t\ge 0$， $N^{\prime }\left(t\right)\equiv 0$，且 $0<q<1$，从而如若 $S\left(0\right)>0$，则对任意的 $t\ge 0$，总有 $S\left(t\right)>0$。此外，对于任意的 $t\ge 0$，也有 $I\left(t\right)>0$，如果假设不成立，则存在 ${\tilde{t}}_0>0$ 使得 $I\left({\tilde{t}}_0\right)=0$。令 $t_0=\mathrm{int}\left\{{\tilde{t}}_0:I\left({\tilde{t}}_0\right)=0\right\}$，则当 $t\in \left[0,t_0\right)$ 时，有 $I\left(t_0\right)=0$ 和 $I\left(t\right)>0$。由上述 $I(t)$ 的形式解的右端表达式可得 $I\left(t_0\right)>0$，这与 $I\left(t_0\right)=0$ 矛盾。从而，对任意的 $t\ge 0$， $I\left(t\right)>0$。即模型(2)的解 $\left(S\left(t\right),I\left(t\right)\right)$ 是非负的。

考虑到生物学意义，仅在区域 $\Omega =\left\{\left(S,I\right):S\ge 0,I\ge 0,S+I\le 1\right\}$ 内研究模型(2)的解的动力学性态，显然 $\Omega$ 是模型(2)的正向不变集。

3. 准备工作

3.1. 平衡点的存在性

假设 $\left(S\left(t\right),I\left(t\right)\right)$ 为模型(2)满足初值条件(3)的解，并且对任意的 $t\ge 0$， $S\left(t\right)\ge 0$， $I\left(t\right)\ge 0$ 成立，模型(1)的平衡点满足方程组：

$\{\begin{array}{l}\mu -\beta SI-\mu S-\mu qI=0\hfill \\ \beta SIT\left(\tau \right)-\mu I=0\hfill \end{array}$

其中 $T\left(\tau \right)={\displaystyle {\int }_0^{\tau }f\left(\xi \right)e^{-\mu \xi }\text{d}\xi }$。

令：

$R_0=\frac{\beta T\left(\tau \right)}{\mu }$

则 $R_0$ 为模型(2)的基本再生数。

定理3.1 当 $R_0\le \text{1}$ 时，总存在无病平衡点 $E_0=\left(1,0\right)$。当 $R_0>\text{1}$ 时，模型(2)除 $E_0$ 外还存在唯一的地方病平衡点 $E_{+}=\left(S^{*},I^{*}\right)$，其中：

$S^{*}=\frac{1}{R_0},I^{*}=\frac{\mu \left(R_0-1\right)}{\beta +R_{0}q\mu }$

3.2. 无病平衡点的全局稳定性

定理3.2当 $R_0\le \text{1}$ 时，无病平衡点 $E_0$ 是全局稳定的。当 $R_0>\text{1}$ 时， $E_0$ 是不稳定的。

证明：取Lyapunov函数，可得：

$V\left(S\left(t\right),I\left(t\right)\right)=I\left(t\right)+{\displaystyle {\int }_t^{t+\xi }\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)}}{e}^{-\mu \xi }S\left(x-\xi \right)I\left(x-\xi \right)\text{d}\xi \text{d}x$ (4)

$V\left(t\right)$ 是正定的，且有 $V\left(E_0\right)=0$。

$V\left(t\right)$ 沿模型(2)的解轨线求导可得：

$\begin{array}{c}{V}^{\prime }\left(t\right)=-\mu I\left(t\right)+\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)e^{-\mu \xi }S\left(t\right)I\left(t\right)\text{d}\xi }\\ =\left(\beta S\left(t\right){\displaystyle {\int }_0^{\tau }f\left(\xi \right)e^{-\mu \xi }\text{d}\xi }-\mu \right)I\left(t\right)\\ =\left(\beta S\left(t\right)T\left(t\right)-\mu \right)I\left(t\right)\\ =\mu \left(R_{0}S\left(t\right)-1\right)I\left(t\right)\end{array}$ (5)

由模型(2)第一个方程可得：

$S^{\prime }\left(t\right)\le -\mu S\left(t\right)+\mu .$

由比较原理 [20] 可得 $S\left(t\right)\le 1$。由 $R_0\le 1$ 可得 $V^{\prime }\left(t\right)\le 0$，由Lyapunov-Lasalle不变性原理 [21] 可知 $E_0$ 在 $\Omega$ 内为全局稳定的。

模型(2)在 $E_0$ 点处的线性化系统所对应的特征方程为：

$f\left(\lambda \right)=\left(\mu +\lambda \right)-\beta {\displaystyle {\int }_0^{T}f\left(\xi \right)e^{-\left(\lambda +\mu \right)\xi }}\text{d}\xi .$

从而：

$f\left(0\right)=\mu -\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)}{e}^{-\left(\lambda +\mu \right)\xi }\text{d}\xi =\mu \left(1-\frac{\beta {\displaystyle {\int }_0^{T}f\left(\xi \right)e^{-\mu \xi }}\text{d}\xi }{\mu }\right)<0.$

当 $R_0>1$ 时，可得：

$f\left(0\right)<0,\underset{\lambda \to +\infty }{\lim }f\left(\lambda \right)=+\infty$

由此可知，模型(2)至少存在一个正实部的特征根 ${\lambda }_{\text{0}}$，使得 $f\left({\lambda }_0\right)=\text{0}$，即无病平衡点 $E_0\left(1,0\right)$ 是不稳定的。

3.3. 模型解的持久性

由于是在 $\Omega$ 内考虑模型(2)，为证明模型解的持久性，只需证明 $S\left(t\right)$ 与 $I\left(t\right)$ 具有正常数下界。

引理3.1 具有初始条件(3)的模型(2)的解 $\left(S\left(t\right),I\left(t\right)\right)$ 满足：

$S\left(t\right)\ge \frac{\mu p}{\mu +\beta }>\begin{array}{cc}\text{0}& \left(0<t<+\infty \right)\end{array}.$ (6)

证明：在 $\Omega$ 内，由模型(2)的第一个方程可得：

$S^{\prime }\left(t\right)\ge \mu p-\left(\mu +\beta \right)S\left(t\right).$

由比较原理可得：

$S\left(t\right)\ge \frac{\mu p}{\mu +\beta }.$

引理3.2 当 $R_0>1$ 时，具有初值条件(3)的模型(2)的解 $\left(S\left(t\right),I\left(t\right)\right)\left(t\ge 0\right)$ 满足：

$I\left(t\right)\ge \epsilon e^{-\left(\mu +\beta \right)\left(T_0+\tau \right)}\left(0<t<+\infty \right)$ (7)

由定理3.2可知，当 $R_0>1$ 时， $E_0$ 是不稳定的，从而 $I\left(t\right)$ 有以下三种情况：

1) 存在 $T_0$，当 $t>T_0$ 时， $I\left(t\right)\le \epsilon$ ；

2) 存在 $T_0$，当 $t>T_0$ 时， $I\left(t\right)\ge \epsilon$ ；

3) 存在 $T_0$，当 $t>T_0$ 时， $I\left(t\right)$ 关于 $\epsilon$ 震荡。

情况(1)：

此时 $I\left(t\right)\le \epsilon ,t\ge t_0\ge T_0$，不成立，如若不然，由模型(2)的第一个方程可得：

$S\left(t\right)\ge \frac{\mu \left(1-q\epsilon \right)}{\mu +\epsilon \beta }.$

令：

$\lambda =\frac{\mu \left(1-q\epsilon \right)}{\mu +\epsilon \beta }$

则：

$S\left(t\right)\ge \lambda .$ (8)

当 $t\ge T_0+\tau$ 时，由式(5)和式(8)可得：

$V^{\prime }\left(t\right)\ge \mu \left(\frac{\lambda \beta T\left(\tau \right)}{\mu }-1\right)I\left(t\right)=\mu \left(\lambda R_0-1\right)I\left(t\right),$

当 $R_0>1$， $\epsilon$ 很小时，可得 $\lambda R_0-1>0$。

定义：

$I=\min I\left(T_0+\tau +\theta \right).$

下证 $I\left(t\right)\ge I\left(t\ge T_0+\tau \right)$。如若不成立，则存在 $T>0$，使得：

$I\left(t\right)\le I\left(T_0+\tau \le t\le T_0+\tau +T\right),I\left(T_0+\tau +T\right)=I,I^{\prime }\left(T_0+\tau +T\right)\le 0.$

另外，由模型(2)的第二个方程可得：

${\left(\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right){\mathrm{e}}^{-\mu \xi }S\left(t\right)I\left(t\right)\text{d}\xi -\mu I\left(t\right)}\right)|}_{T_0+\tau +T}\ge \mu \left(\lambda R_0-1\right)I>0$

矛盾。因此可得：

$I\left(t\right)\ge I\left(t\ge T_0+\tau \right).$

当 $t\ge T_0+\tau$ 时：

$V^{\prime }\left(t\right)>\mu \left(\frac{\lambda \beta T\left(\tau \right)}{\mu }-1\right)I=\mu \left(\lambda R_0-1\right)I>0$

此式表明 $V\left(t\right)$ 无界，而在 $\Omega$ 内由式(3)知 $V\left(t\right)$ 有界，矛盾，从而情况(1)不成立。

情况(2)：

存在 $T_0$，当 $t\ge T_0$ 时，若 $I\left(t\right)\ge \epsilon$，可得 $I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}$，故 $I\left(t\right)$ 是有下界的。

情况(3)：

存在 $T_0$，当 $t\ge T_0$ 时， $I\left(t\right)$ 关于 $\epsilon$ 震荡，此时 $I\left(t\right)$ 也是有下界的。

事实上，存在 $t_{\text{1}}>T_0,t_2>T_0$ 使得 $I\left(t_{\text{2}}\right)=I\left(t_{\text{1}}\right)=\epsilon$，当 $t\in \left(t_1,t_2\right)$ 时 $I\left(t\right)<\epsilon$。

如果 $t_2-t_1\le T_0+\tau ,t\in \left(t_1,t_2\right)$，由 $I^{\prime }\left(t\right)\ge -\mu I\left(t\right),I\left(t_1\right)=\epsilon$，有 $I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}$。

如果 $t_{\text{2}}-t_{\text{1}}>T_0+\tau$，当 $t_{\text{1}}\le t\le t_{\text{1}}+\tau +T_0$ 时，仍有 $I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}$。

当 $t\in \left(t_1+\tau +T_0,t_2\right)$ 时，若 $I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}$ 不成立，则存在一个 $T^{*}>0$，使得：

$I\left(t\right)\le \epsilon e^{-\mu \left(T_0+\tau \right)},I\left(t_1+T_0+\tau +T^{*}\right)=\epsilon e^{-\mu \left(T_0+\tau \right)}$

从而 $I^{\prime }\left(t_1+T_0+\tau +T^{*}\right)\le 0$。

由模型(3)的第二个方程可得：

$\begin{array}{c}{I}^{\prime }\left(t_1+\tau +T_0+T^{*}\right)={\left(\beta {\displaystyle {\int }_0^{\tau }f\left(\xi \right)S\left(t-\xi \right)I\left(t-\xi \right)}{e}^{-\mu \xi }\text{d}\xi -\mu I\left(t\right)\right)|}_{t_1+\tau +T_0+T}\\ \ge \mu \epsilon e^{-\mu \left(\tau +T_0\right)}\left(\frac{\lambda \beta T\left(\tau \right)}{\mu }-1\right)\\ =\mu \epsilon e^{-\mu \left(\tau +T_0\right)}\left(\lambda R_0-1\right)>0\end{array}$

矛盾。

故当 $t\in \left(t_1+\tau +T_0,t_2\right)$ 时， $I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}$ 成立，从而对于任意的 $t\in \left(t_{\text{1}},t_{\text{2}}\right)$，有：

$I\left(t\right)\ge \epsilon e^{-\mu \left(T_0+\tau \right)}.$

定理3.3 结合引理3.1和引理3.2，从而当 $R_0>1$ 时，具有初值条件(3)的模型(2)的解是一致持久的，其中：

$S\left(t\right)\ge \frac{\mu p}{\mu +\beta },I\left(t\right)\ge \epsilon e^{-\left(\mu +\beta \right)\left(T_0+\tau \right)}\left(0<t<+\infty \right)$ (9)

4. 数值模拟

下面对定理3.2，定理3.3的结果进行验证，参数取值主要来源于文献 [19] 。

在模型(1)中取 $f\left(s\right)=\delta \left(s-\tau \right)$，这里的 $\delta$ 是狄拉克函数，模型(1)可以简化为如下模型：

$\{\begin{array}{l}{S}^{\prime }\left(t\right)=\mu -\beta S\left(t\right)I\left(t\right)-\mu S\left(t\right)-\mu qI\left(t\right)\hfill \\ E^{\prime }\left(t\right)=\beta S\left(t\right)I\left(t\right)-\beta S\left(t-\tau \right)I\left(t-\tau \right)e^{-\mu \tau }+q\mu I\left(t\right)-\mu E\left(t\right)\hfill \\ I^{\prime }\left(t\right)=\beta S\left(t-\tau \right)I\left(t-\tau \right)e^{-\mu \tau }-\mu I\left(t\right)\hfill \end{array}$ (10)

(1) 当 $R_0\le \text{1}$ 时，模型(1)的无病平衡点 $E_0$ 是全局渐近稳定的。

模型(10)中各参数取值如下： $\beta =1.8,\mu =0.35,\tau =1,q=0.8$。初值为： $S=0.5,E=0,I=0.5$。经计算， $R_0<1$。由定理3.2可知，模型(1)的无病平衡点 $E_0$ 是全局渐近稳定的，数值模拟结果如图1所示。

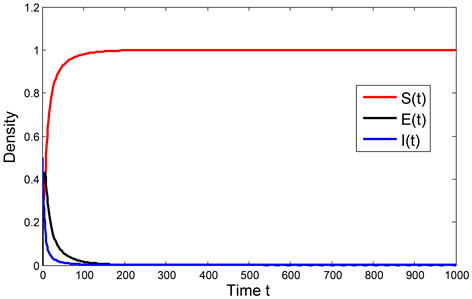
Figure 1. Global stability of the disease-free equilibrium point to the system (1) with $R_0<1$

图1. 当 $R_0<1$ 时系统(1)的无病平衡点的全局稳定性

(2) 当 $R_0>1$ 时，模型(1)的解的一致持久性

模型(10)中各参数取值如下： $\beta =1.7,\mu =0.35,\tau =1,q=0.8$，初值为： $S=0.5,E=0,I=0.5$。经计算， $R_0>1$。由定理3.3，模型(1)的解是持久的，且当t趋于无穷大时，疾病将形成地方病。数值模拟结果如图2所示。

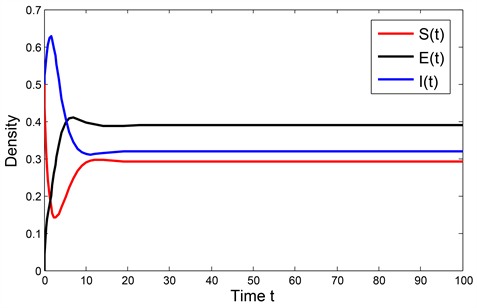
Figure 2. Persistence of the solution to the system (1) with $R_0>1$

图2. 当 $R_0>1$ 时系统(1)解的持久性

图1、图2分别验证了模型(1)无病平衡点的全局渐近稳定性和模型解的持久性，并表明了当感染率较高时，会提高疾病基本再生数，进而使得僵尸鹿传染病继续蔓延形成地方病，因此为了控制僵尸鹿传染病的继续蔓延，可以通过人为猎杀或者焚毁已患病的僵尸鹿的方式，来降低疾病感染率，从而达到控制僵尸鹿疫情的目的。

(3) 僵尸鹿病毒潜伏期和死亡率对鹿种群数量(密度)的影响

模型(10)中各参数取值如下： $\beta =\text{1}\text{.7,}q=\text{0}\text{.8}$，初值为： $S=0.5,E=0,I=0.5$。数值模拟结果如图3所示。

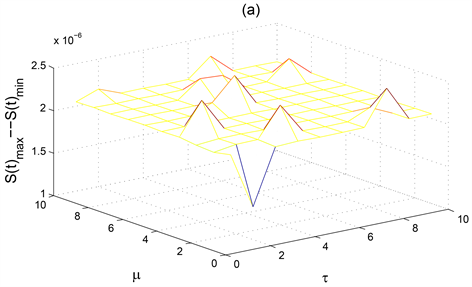
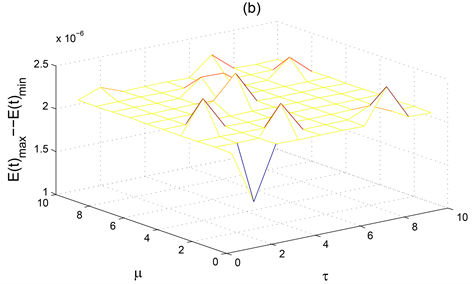
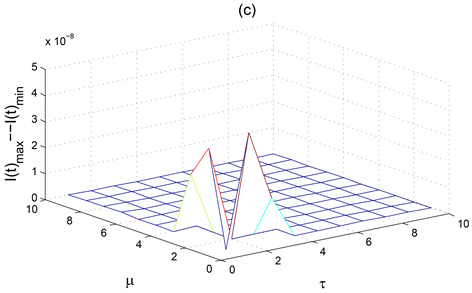
Figure 3. The ultimate oscillation interval of the solution to the system (1) when $\tau ,\mu$ increases simultaneously

图3. 当 $\tau ,\mu$ 同时增加时系统(1)解的最终震荡区间

图3显示了僵尸鹿种群数量的稳定性随着自身死亡率 $\mu$ 和病毒潜伏期 $\tau$ 的变化而变化。图3(c)显示了患病僵尸鹿种群数量随着自身死亡率 $\mu$ 和病毒潜伏期 $\tau$ 的变化会有两次大的振幅出现，表示此时患病僵尸鹿种群 $I\left(t\right)$ 是不稳定的，尤其是当病毒潜伏期 $\tau$ 为2，死亡率 $\mu$ 达到1时，患病僵尸鹿种群 $I\left(t\right)$ 的振幅达到最大。图3(c)显示了当 $\left(\tau ,\mu \right)\in \left[0,4\right]\times \left(0,4\right]$ 时，患病僵尸鹿种群 $I\left(t\right)$ 是不稳定的。从而适当控制患病鹿种群的死亡率 $\mu$ 以及较短的僵尸鹿病毒潜伏期 $\tau$ 可以有效控制患病鹿群的种群数量。图3(a)则显示了患病鹿种群 $I\left(t\right)$ 较高的死亡率和较小的病毒潜伏期 $\tau$ 对稳定健康鹿种群的数量是有益的。

5. 结论

依据北美僵尸鹿疫情传播的特点，建立了具有垂直传染和分布时滞的SEI传染病模型，通过构造Lyapunov函数和运用Lyapunov-Lasella不变性原理获得了模型无病平衡点的全局渐近稳定性与模型解的持久性。在此基础上，通过比较原理得到了易感鹿种群数量的正的下界。数值模拟图1和图2分别展示了当感染率较高时，会增大疾病基本再生数 $R_0$ 的取值，进而使得僵尸鹿传染病继续蔓延形成地方病。图3展示了：适当控制患病鹿种群的死亡率 $\mu$ 以及较短的僵尸鹿病毒潜伏期 $\tau$ 不仅可以有效控制患病鹿群 $I\left(t\right)$ 的种群数量，还可以稳定健康鹿种群 $S\left(t\right)$ 的数量。从而为了控制僵尸鹿传染病的继续蔓延，降低疾病感染率，可以通过人为猎杀或者焚毁已患病的僵尸鹿的方式，达到控制僵尸鹿疫情的目的。

致谢

在此感谢东北石油大学——人才引进科研启动经费资助项目(项目代码：1305021838)的支持。