1. 引言
弦图自20世纪50年代产生于稀疏线性系统的研究中,其历史与半定优化的历史有重要关联。Parter S曾将图的“弦化1”与求解线性方程组的高斯消去法对应起来,由图“弦化”的复杂性来估计求解线性方程组的复杂性 [1]。弦图的概念被提出来后,许多学者研究发现弦图的应用与变量消除相辅相成,任意图的变量消除过程都可以对应其“弦化”过程。变量消除在许多应用中是一种自然的方法,基于不同形式的变量消除的各种算法可以通过图中节点的删除来描述和分析,这在一定程度上解释了弦图研究的学科多样性。之后Rose D J对弦图上的变量消除以及弦图的特殊性质做了一个介绍,给出了弦图完美消除序列的概念,弦图上的完美消除序列可以在不引入填充边的情况下完成变量消除 [2]。弦图变量消除的其中一个应用是概率图模型,在概率图模型上,概率计算可以以变量消除的形式出现,而在以弦图为模型的概率计算中,弦图的完美消除序列就是计算代价最小的变量消除推理的消除顺序,这也说明了关于完美消除序列的研究意义 [3]。
近年来,大量学者发现以弦图为研究对象时,图论问题会变得更加容易解决,于是,学者们开始在弦图上讨论图论中的组合问题:最大团、最大独立集、k着色等;同时,基于弦图结构的研究也获得了一些进展,Rouzbahani Malayeri M已经证明了弦图的二项式边理想的正则性上界 [4],Arvind V已经证明弦图GI (graph isomorphism,图同构)问题的复杂性以叶龄为参数 [5];并且,弦图子类在图论问题上的表现也是近年的热点问题,Liu C H已经给出了罗马支配问题在强弦图上的线性时间算法 [6],Uehara R已经证明GI问题在弦二部图和强弦图上是GI完全的 [7];此外,弦图在许多领域都有应用,包括编译器构造和数据库 [8]。
k树是弦图的一个特殊子类,同时k树作为树这一概念的扩展,可以作为很多图论问题的模型,而k树本身的特殊结构在约束满足问题,组合问题等问题上存在多项式时间算法。目前对于k树的研究主要集中于部分k树(树宽由k限定的图),Telle J A已经将部分k树上的算法设计应用于顶点划分问题,得到了以树宽为时间复杂性参数的算法 [9]。k树作为有特殊结构的弦图子类,在某些问题上会比弦图发挥更好的性能,后续可以进一步研究。
本文启发于Rose D J在文献 [2] 里提出的“k树是弦图的一个子类”,于是,“具有特殊结构的弦图子类——k树的完美消除序列的特殊性质”成为了一个研究方向。本文主要证明了以下结果:
定理1 任取k树 ,其完美消除序列可通过迭代地删除其中的k度点来刻画(即首先删除
,其完美消除序列可通过迭代地删除其中的k度点来刻画(即首先删除 中的一个k度点,得到
中的一个k度点,得到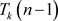 ,再删去
,再删去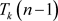 中的一个k度点,得到
中的一个k度点,得到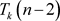 ,重复该操作,直至所得图为k个节点,最后按任意顺序删除这k个节点,该删除顺序就是其完美消除序列)。
,重复该操作,直至所得图为k个节点,最后按任意顺序删除这k个节点,该删除顺序就是其完美消除序列)。
定理2 任取k树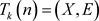 及
及 的序列
的序列 ,
, 标记X为
标记X为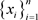 ,则
,则 是
是 的完美消除序列,当且仅当
的完美消除序列,当且仅当 满足:
满足:
1)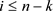 时,
时,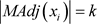 ,即
,即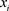 与
与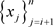 里的一个k团中的每一个节点均连接;
里的一个k团中的每一个节点均连接;
2)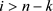 时,
时,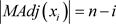 ,即
,即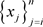 是团。
是团。
定理2给出了k树完美消除序列的特点,k树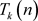 的节点按照完美消除序列排序后满足1)
的节点按照完美消除序列排序后满足1) 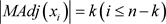 ;2)
;2)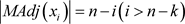 ,由此可知k树的所有完美消除序列都满足定理1中的k度点的删除顺序,换而言之,通过定理1节点删除的方式可以找到k树的所有完美消除序列。
,由此可知k树的所有完美消除序列都满足定理1中的k度点的删除顺序,换而言之,通过定理1节点删除的方式可以找到k树的所有完美消除序列。
定理3 k树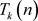 的完美消除序列集合与构造过程集合之间存在双射,且两个集合的元素之间以互为逆序的方式一一对应。
的完美消除序列集合与构造过程集合之间存在双射,且两个集合的元素之间以互为逆序的方式一一对应。
定理3给出了k树的完美消除序列与构造过程之间的关系。根据定理3的结论,可以从完美消除序列的角度去分析k树的构造过程,可以通过刻画k树的完美消除序列来刻画k树的构造过程,也可以通过计算k树完美消除序列的个数来计算k树构造过程的个数。
2. 基础知识
本文用 来表示一个无向图,其中,X是一个非空有限的节点集合,E是X中成对节点的集合,E中节点对
来表示一个无向图,其中,X是一个非空有限的节点集合,E是X中成对节点的集合,E中节点对 由无向边
由无向边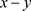 连接(本文基于无向图进行讨论,后续简称无向图为图)。在图
连接(本文基于无向图进行讨论,后续简称无向图为图)。在图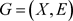 中,任取一个含于X的非空节点集合C,如果C里任意两个节点都在G中连接,则称C为一个团(后续简称k个节点构成的团为k团),如果X里任意两个节点都在G中连接,则称G为完全图。
中,任取一个含于X的非空节点集合C,如果C里任意两个节点都在G中连接,则称C为一个团(后续简称k个节点构成的团为k团),如果X里任意两个节点都在G中连接,则称G为完全图。
一个双射 被叫做图G的序列,令
被叫做图G的序列,令 是
是 的逆映射,
的逆映射,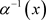 定义为节点x对应的序列号。可以根据序列
定义为节点x对应的序列号。可以根据序列 标记点集X,并且得到点集X的一个表示:
标记点集X,并且得到点集X的一个表示: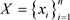 。在图
。在图 中,如果对每一个
中,如果对每一个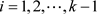 ,都有
,都有 ,即
,即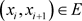 ,则
,则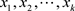 称为G的一条路径。在图
称为G的一条路径。在图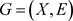 中,如果节点
中,如果节点 与节点
与节点 可以通过一条路径连接,则称
可以通过一条路径连接,则称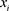 与
与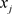 连通,如果点集X里任意两个节点都连通,则称图G为连通图(本文基于连通图进行讨论),如果路径
连通,如果点集X里任意两个节点都连通,则称图G为连通图(本文基于连通图进行讨论),如果路径 满足
满足 ,则
,则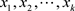 称为图G的一个环,且环长为
称为图G的一个环,且环长为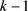 ,以下基于环长给出弦图的定义。
,以下基于环长给出弦图的定义。
定义1 [3] 令 是图
是图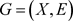 中的一个环,环中的一条弦是连接两个不连贯节点
中的一个环,环中的一条弦是连接两个不连贯节点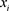 与
与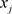 的一条边,对
的一条边,对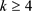 ,如果任意环
,如果任意环 有一条弦,那么图G称为弦图。
有一条弦,那么图G称为弦图。
对于图 和子集
和子集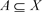 ,有导出子图
,有导出子图 ,其中
,其中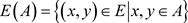 。对于图
。对于图 以及节点
以及节点 ,用
,用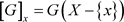 表示图G删除节点x及其连接边所得到的图。图
表示图G删除节点x及其连接边所得到的图。图 的一个割S是使得导出子图
的一个割S是使得导出子图 有两个及以上连通分支的X的子集,且连通分支可以表示为
有两个及以上连通分支的X的子集,且连通分支可以表示为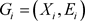 ,导出子图
,导出子图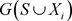 就是图G相对于割S的叶。图G的一个
就是图G相对于割S的叶。图G的一个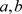 割是使得节点a与节点b分别在不同分支的割,图G的一个极小割是不存在真子集是割的一个割。关于割,Rose D J。已证明以下结果:
割是使得节点a与节点b分别在不同分支的割,图G的一个极小割是不存在真子集是割的一个割。关于割,Rose D J。已证明以下结果:
定理4 [2] 一个图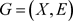 ,G带有割团S和叶
,G带有割团S和叶 ,若
,若 是
是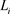 的割,则
的割,则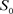 也是图G的割,若
也是图G的割,若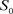 是
的一个极小
割,则
也是图G的一个极小
割。
是
的一个极小
割,则
也是图G的一个极小
割。
本文用
表示节点
在图G中相邻节点(简称邻节点)的集合,用
表示节点
在图G中邻节点的个数,并称其为度。用
表示节点
在图G中的单调相邻节点(简称单调邻节点)的集合。在图
中,对任意节点
,其邻节点集合
里不相邻的成对节点的集合,表示为
,并称为亏数,而满足
的节点x被称为单纯点。相应的,其单调邻节点集合
里不相邻的成对节点的集合,表示为
,并称为单调亏数。
定义2 [2] 取图
的一个序列
,
标记点集X为
,如果满足对任意节点
,都有
,则称序列
是图G的一个完美消除序列。
定理5 [2] 一个图
是弦图当且仅当图G存在序列
,使得
是G的完美消除序列。
下面给出本文的中心——k树的定义。
定义3 [10] k树的定义如下:
1) k个节点的k树是k个节点的完全图;
2) 给定任意n个节点的k树
,可以通过连接第
个节点与
中某个k团的所有节点,得到
个节点的k树
。
(由k树的递归定义可知,每一个k树都有一个k团作为初始状态,该k团被称为k树的初始团。)
定理6 [10] 一个图
是一个k树当且仅当
1) 图G是连通图;
2) 图G有一个k团但没有
团;
3) 图G的每一个极小
割都是一个k团。
3. 定理1和定理2的证明
为了讨论k树的完美消除序列,本文先证明了关于k树和完美消除序列的几个引理。引理2的证明过程对k树的结构有一个初步的分析。引理3进一步分析了完美消除序列在k树上的特点。
引理1一个完全图的任意序列都是其完美消除序列。
证 任取完全图
,其中
,任取X的序列
,由
标记X为
,易知
,于是
是个团,从而
,故
是完全图G的完美消除序列。由
的任意性,引理得证。
引理2 k树是弦图。
证 任取n个节点的k树
,令
表示
的构造过程,由
的构造过程标记X为
,其中
是k树的初始团,
代表构造
时在
上添加的节点,令
表示节点
连接的
中的k团,且
,则有
.
易知
是团,从而
,由定义2可知
对应的序列就是k树
的完美消除序列,由定理5可知k树是弦图。
引理3在节点个数大于k的k树中,一个节点是单纯点当且仅当它的度为k。
证 任取k树
,当
时,易知
是个完全图,其节点均为k度,同时均为单纯点,命题成立。下面对
时的情况进行证明。
设k树
,由
的构造过程标记X为
,其中
是k树的初始团,由构造过程可知
也是个团。令
表示引入
时,与
相连接的k团。下面将X分为
和
分别进行讨论。在
里,已知
是个团,由
的构造过程可知,设节点
是
里的k度点,则
一定不含于后续连接团,即
(因为
是个团,
至少有k个邻节点,
若
含于后续连接团,则其度一定大于k),于是有
,易知
是个团,从而
。在
里,
里的节点在引入时就已经连接了一个k团,设节点
是
里
度为k的节点,则
一定不含于后续连接团,即
,于是有
,而
是引入
时,
所连接的k团,于是
。综上,
中的k度点x均满足
,均为单纯点。
反之,由
的构造过程易知
的任意节点x均满足
(因为
的节点集合由构造过程排序后,前
个节点本身构成了一个
团,它们的度至少为k,后
个节点,在引入的时候就已经与一个k团相连接,它们的度也至少为k)。假设存在度大于k的单纯点y,那么
是个团,且
,这与定理6中k树没有
团的性质相矛盾,所以
中单纯点的度均为k。
综上,引理得证。
引理4任意节点个数大于k的k树去掉一个k度点还是k树。
证 任取k树
。当
时,易知
是个完全图,其节点的度均为k,
去掉一个k度点后,变为k个节点的完全图,依旧是k树,命题成立。当
时,设k树
,由
的构造过程标记X为
,其中
是k树的初始团,由构造过程可知
也是个团。令
表示引入
时,与
相连接的k团。这里任取
中的k度点x,由引理3可知
,
是一个k团。令
,下面证明图G有以下三个性质:
1) 假设G不连通,则易知G的不连通是由于节点x的删除导致的,所以
里至少有两个节点不连通。而
是一个k团,里面的节点两两相连,与假设矛盾,所以图G是连通图;
2) 由引理3可知
里的k度点不出现在后续连接团里,而
,所以连接团
里没有k度点,即
,从而G有k大小的团
,图G是k树
删除节点x得到的,而
作为k树不包含
大小的团,故G没有
大小的团;
3) 由割和叶的定义可知,G是相对于割团
的叶,由定理4可知G中任意一个极小
割也是
中的极小
割,而
是k树,由定理6可知,
中的极小
割均为k团,从而G中的极小
割也均为k团。
于是,由定理6可知图G是k树。
综上,引理得证。
定理1的证明 任取k树
。当
时,
是k个节点的k树,此时
是一个完全图,由引理1可知,
里节点的任意序列都是其完美消除序列,命题成立。
当
时,
是
个节点的k树,由k树的构造过程可知,此时
的节点集合X是一个
团,且每个节点的度均为k,任选一个k度点删除,得到一个k团,可以按任意顺序删除这k个节点。这
个节点的删除顺序就是其完美消除序列,命题成立。
假设
时,命题成立。则当
时,
,
,任取
里的k度点x,由引理3可知
,由引理4可知
是l个节点的k树,于是由假设可知,
可以通过迭代地删除k度点,直至剩余k个节点,最后按任意顺序删除这k个节点的方式标记
为
,且
对应的序列就是
的完美消除序列,满足
。这里标记
,标记
,则
,且有1)
;2)
。由定义2,
所对应的序列就可以作为
的完美消除序列。由k度点x选择的任意性和
序列的构造过程,命题成立。
综上,定理得证。
定理2的证明 首先,设
满足1) 2),则按照序列
对
的节点进行删除时,因为前
个节点满足
,所以每个节点都是作为k度点被删除的,满足定理1中k度点的删除方式,后k个节点的删除也满足定理1中任意顺序的删除方式,于是由定理1可知
是
的完美消除序列。
反之,设
是
的完美消除序列,当
时,
,
是完全图,
是一
个团,对任意
有
,即
时,
,命题成立。
当
时,
,
,由k树的递归构造可知,
是完全图,
是
一个团,对任意
有
,则有:a)
;b)
。命题成立。
假设
时命题成立。当
时,
,
,
标记X为
,则
,
是单纯点,由引理3可知,
是k度点。令
,则
是图G的节点集合,且由引理4及
是k度点可知G是k树,令
,标记
为
,则
,故
对应的序列是G的完美消除序列,而G的节点个数为l,则由假设有:(a)
;(b)
。对于
来讲,
时,
,有
.
时,
,有
.
命题成立。
综上,定理得证。
4. 定理3的证明
一般来说,k树的构造是从k个节点的完全图开始的,本文为了使k树的完美消除序列与构造过程之间的关系有一个更清晰的表达,定义k树的构造从第一个节点开始,下面给出k树构造过程的定义。
定义4对于k树
,取
是一个双射,且根据
标记X为
,通过以下递归步骤:
1)
时,分别连接
与
,使
成为一个团;
2)
时,找
中的一个k团
,使
与
中的每一个节点连接。
得到图G,若
,则称
是
的一个构造过程。
(注意,这里的递归步骤也可以看作是
边集的一个表达)
定理3的证明令A是
的所有完美消除序列的集合,
是
的一个完美消除序列(
是一个双射)。令B是
的所有构造过程的集合,
是
的一个构造过程。令
是A到B的一个映射,满足对
,
,有
,即如果将
看作对X的排序,则
是相对于
的对X的一个逆排序。下面证明
是一个双射。
,
标记X为
,令
,
标记X为
,由
的定义可知
,由
是
的完美消除序列可知:(1)
时,
与
中的一个k团的每一个节点均连接;(2)
时,
是团。相应地,
作为
的逆序序列,满足:1)
时,
与
中的一个k团的每一个节点均连接(即
时,
与
中的一个k团的每一个节点均连接);2)
时,
是团(即
时,
是团)。由定义4可知
是
的一个构造过程,从而有
。
,
标记X为
,令
标记X为
,使得X满足
,由
的定义可知
与
互为逆序序列。由
是
的构造过程可知:1)
时,
与
相连接,
是团;2)
时,
与
中的一个k团的每一个节点均连接。相应地,
作为
的逆序序列满足:1)
时,
与
相连接,
是团(即
时,
与
相连接,
是团);2)
时,
与
中的一个k团的每一个节点均连接(即
时,
与
中的一个k团的每一个节点均连接)。由定理2可知,
是
的一个完美消除序列,从而,
,
使得
。
由
的定义,
将一个序列映射为它的逆序序列,所以对
,有
。
综上,定理得证。
5. k树识别算法
k树识别算法是在弦图识别算法的基础上实现的,先介绍一个弦图识别的算法——MCS (max cardinality search,最大基数搜索)算法 [11]。该算法是弦图识别常用的算法之一(通过最大基数搜索的方式构造序列,并检查该序列是否为一个完美消除序列来判断输入图是否为弦图)。算法如下(算法1)所示:
Algorithm 1. Max-cardinality-search algorithm
算法1. MCS算法
根据k树完美消除序列和构造过程之间一一对应的关系,并且结合k树完美消除序列有关k度点的独特性,给出一个k树的识别算法——先将输入图识别为弦图后,根据其完美消除序列标记其点集,检查是否满足定理2中的结果来确认输入图是否为k树(算法2)。
Algorithm 2. k-trees’ recognition algorithm
算法2. k树的识别算法
6. 结语
本文从k树的递归构造方式入手,证明了作为弦图子类的k树,其完美消除序列具有独特性,可以通过k度点的迭代删除来刻画,k度点的识别相对于单纯点的识别也更加便利。同时,在k树完美消除序列的研究过程中,进一步发现其与k树构造过程之间的关系,k树的每一个完美消除序列都与它的一个构造过程以互为逆序序列的方式一一对应。最后,本文也将k树完美消除序列的独特性应用于k树的识别中,给出了一个k树的识别算法。此外,k树作为有特殊结构的弦图子类,在以弦图为模型的各类问题上会展现更好的性能,后续可以进一步研究。
NOTES
*通讯作者。
1“弦化”表示一个无向图通过加边的方式变为弦图的过程。