APARCH-PET模型的VaR度量

VaR Measure Based on APARCH-PET Models

摘要: 本文提出了一种包含PES的正Edgeworth截断分布(PET)，给出了APARCH-PET模型的VaR表达式，研究了APARCH-PET与经典模型的数据拟合效果。选用上证主板招商银行股票数据进行实证分析，结果表明：PET分布在拟合资产收益率数据的尾部特征时更具优势，构建的APARCH-PET模型能更好的刻画金融资产收益率数据分布的尖峰、厚尾特征和非对称性，且一定程度上提高了VaR度量的预测精度。

Abstract: In this paper, a positive Edgeworth truncated distribution (PET) including PES is proposed, the VaR expression of APARCH-PET model is given, and the data fitting effect of APARCH-PET and classical model is studied. The empirical analysis results show that PET distribution has more advantages in fitting the tail characteristics of asset yield data, and the APARCH-PET model can better depict the spike, thick-tail characteristics and asymmetry of financial asset yield data distribution, and improve the prediction accuracy of VaR measurement to a certain extent.

1. 引言

在金融市场中，我们一般假设扩大100倍的对数收益率服从正态分布，但越来越多的实证分析表明资产收益率数据并不满足对称分布，大多存在明显的尖峰厚尾特征和非对称性。厚尾性表示数据集的尾部比正态分布厚。该现象受到国内外学者持续关注，为了更好地拟合尖峰厚尾特征的资产收益率数据，有学者选用学生t分布、广义误差分布等来拟合，它们的拟合效果与正态分布相比尾部更厚，但这并未有效的解决数据尖峰厚尾性和非对称性。所以，不管从理论上还是实际中，我们对概率分布的研究并提出新的分布函数显得非常重要。

实际金融资产收益率数据存在明显的尖峰厚尾特征，该现象受到国内外学者持续关注。现存文献中，针对资产收益率数据分布的估计主要有：参数法(Bollerslev [1])、非参数法(Silverman [2])和半非参数法(Sargan [3], Mauleón和Perote [4])。参数法要求数据的分布函数形式已知，如假设研究的数据服从正态分布，再根据已知的数据估计正态分布中的参数，这种假设有时并不成立，会存在较大的偏差；非参数法是不考虑总体分布，此时可以避免对总体分布假设不当而导致的偏差，但对于大样本，计算会变得十分复杂；而半非参数法不需要知道数据概率分布的具体形式，在拟合分布时存在一定的优势。因此，利用半非参数法拟合分布是存在意义的。

若序列 $X_1,X_2,\cdots ,X_n$ 独立同分布于 $X~F\left(x\right)$，满足 $\underset{t\to +\infty }{\lim }\text{sup}\left|\mathbb{E}\left({\text{e}}^{itX}\right)\right|<1$，四阶矩 $\mathbb{E}\left(X^4\right)<\infty$，令 $Z_n=\left[\sqrt{n}\left({\bar{X}}_n-\mu \right)\right]/\sigma$，则 $Z_n$ 的二阶Edgeworth [5] 展开式为

$F_n\left(x\right)=\Phi \left(x\right)-\left(\frac{d_1{H}_2\left(x\right)}{\sqrt{n}}+\frac{d_2{H}_3(x)+d_3{H}_5\left(x\right)}{n}\right)\varphi \left(x\right)+O\left(n^{-\frac{3}{2}}\right),$ (1)

其中， $\mu$ 为均值， $\sigma$ 为标准差， $d_1=k_3/6$， $d_2=k_4/24$， $d_3=d_1^2/72$， $k_3=\mathbb{E}{\left(X-\mu \right)}^3/{\sigma }^3$， $k_4=\left(\mathbb{E}{\left(X-\mu \right)}^4-3\right)/{\sigma }^4$， $H_i\left(x\right)$ 为Hermit多项式， $H_2\left(x\right)=x^2-1$， $H_3\left(x\right)=x^3-3x$， $H_5\left(x\right)=x^5-10x^3-15x$， $\Phi \left(x\right)$ 和 $\varphi \left(x\right)$ 分别为标准正态分布的分布函数和概率密度函数。Edgeworth展开式将总体的偏度和峰度参数融入其中，能较好地刻画数据尖峰厚尾特征。Ñíguez [6] 提出了正的Edgeworth-Sargan分布(PES)，León [7] 研究了变换Gram Charlier分布(TGC)及应用。

Bollerslev [8] 首次提出GARCH模型用于刻画金融数据波动率的聚集特征，此后，针对该模型的拓展和应用形成了丰富的GARCH簇模型，如Nelson [9] 和Ding [10] 分别提出EGARCH与APARCH模型，用于克服金融资产收益率正负的非对称效应；魏正元 [11] 将EGARCH模型与广义Pareto分布的极值理论结合，构建EGARCH-PED模型测算了收益率的VaR值，该方法在一定程度上提高了VaR估计的预测精度；鲁皓 [12] 提出用GARCH-GED模型来度量证券投资风险；宫晓莉 [13] 用GJR-GARCH-GED模型拟合资产收益率的边际分布，构建GARCH-copula模型，分析了两个模型对金融序列的拟合效果，度量了投资组合风险值。

受文献 [5] 和 [6] 的启发，本文基于Edgeworth展开的思想，新提出了一类正Edgeworth截断分布，计算出了新分布密度函数、分布函数和k阶矩的函数表达式，并计算出参数的最大似然估计量。新分布包含了数据的峰度与偏度两个参数，在拟合尾部较厚的数据上比正态分布更合适。将PET分布刻画到模型的残差序列，建立了APARCH-PET模型用于估计收益率序列的VaR值。选取上证主板招商银行股票收盘价格数据，对比分析了APARCH-norm，APARCH-PES，APARCH-PET三种模型拟合效果，计算出了相应的VaR，并对VaR做了返回测试。结果表明，采用正态分布拟合残差序列的模型低估了风险值，而采用PET分布拟合残差序列的模型度量的VaR更准确。一定程度上提高VaR的准确度，可以防止投资者过度投资，从而避免一些金融交易中的重大亏损。

2. PET分布

定义1. 若随机变量X的密度函数为

$f\left(x\right)=\frac{1}{\xi }\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right),$ (2)

其中， $\xi =1+3!d_1^2+4!d_2^2+6!d_3^2$，则称X服从正Edgeworth截断分布，简称PET。

(a) PET概率密度函数图(d₁ = 0, d₂ = 0.04, 0.06, 0.10, 0.20) 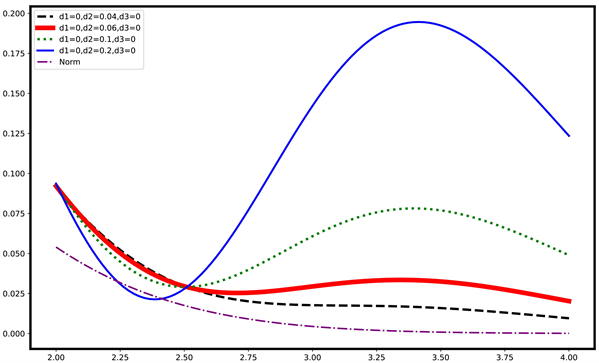(b) PET概率密度函数图(d₁ = 0, d₂ = 0.04, 0.06, 0.10, 0.20) 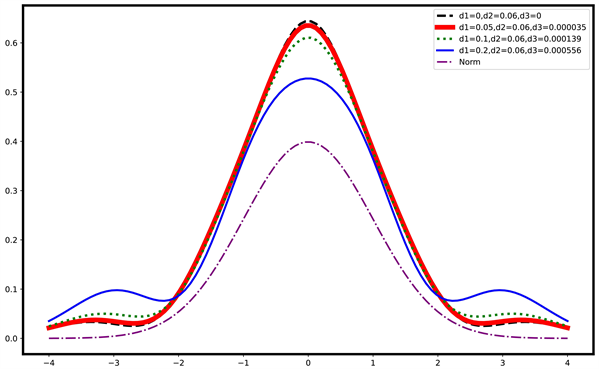(c) PET概率密度函数图(d₂ = 0.06, d₁ = 0, 0.05, 0.10, 0.20)(d) PET右尾概率密度函数图(d₂ = 0.06, d₁ = 0, 0.05, 0.10, 0.20)

Figure 1. Diagram of the PET density function with different parameters

图1. 不同参数下的PET密度函数图

注. 图1给出不同参数下的PET概率密度函数图。图1(a)与图1(b)表示参数 $d_1=0$， $d_2=0.04$ (虚线)，0.06 (粗实线)，0.10 (点线)，0.20 (细实线)的PET概率密度函数图与右尾概率密度图。可以看出，固定参数 $d_1$，PET函数图像随着 $d_2$ 增大，尾部将增厚，且由单峰变为多峰。

图1(c)与图1(d)表示参数 $d_2=0.06$， $d_1=0$ (虚线)，0.05 (粗实线)，0.10 (点线)，0.20 (细实线)的PET概率密度图和右尾概率密度图。可以看出，固定参数 $d_2$，PET函数图像会随着 $d_1$ 的增大，尾部增厚，峰度递减。不同参数下，与标准正态分布(点横线)相比，PET分布的尾部更厚。当 $d_1$ 趋于0时，PET分布将退化为 $q=2$ 时的PES分布。

注2. 不难验证(2)式右边积分为1

$\begin{array}{c}f\left(x\right)={{\displaystyle \int }}_{-\infty }^{\infty }\frac{1}{\xi }\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x\%\\ =\frac{1}{\xi }\left(1+3!d_1^2+4!d_2^2+6!d_3^2\right)\\ =1.\end{array}$

命题1. PET的分布函数如下，证明见附录

$\begin{array}{c}F\left(x\right)=\mathbb{P}\left(X\le x\right)\\ ={\displaystyle {\int }_{-\infty }^x\frac{1}{\xi }}\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x\\ =\frac{1}{\xi }[\left(1+3!d_1^2+4!d_2^2+6!d_3^2\right)\Phi \left(x\right)-{\displaystyle \underset{i=0}{\overset{2}{\sum }}\frac{3!d_1^2}{(3-i)!}{H}_{3-i}}\left(x\right)H_{2-i}\left(x\right)\varphi \left(x\right)\\ -{\displaystyle \underset{i=0}{\overset{3}{\sum }}\frac{4!d_2^2}{\left(4-i\right)!}{H}_{4-i}\left(x\right)H_{3-i}\left(x\right)\varphi \left(x\right)}-{\displaystyle \underset{i=0}{\overset{5}{\sum }}\frac{6!d_3^2}{(6-i)!}{H}_{6-i}\left(x\right)H_{5-i}\left(x\right)\varphi \left(x\right)}].\end{array}$

命题2. 假设随机变量X服从PET，k阶矩为(证明见附录)

当k为奇数时，

$m_k=\mathbb{E}\left(X^k\right)=0;$

当k为偶数时，

$m_k=\mathbb{E}\left(X^k\right)=\frac{1}{\xi }\left({\mu }_k+d_1^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}3!c_{i}i!}+d_2^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}4!c_{i}i!}+d_3^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}6}!c_{i}i!\right).$

其中， $x^k={\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)$， $c_i$ 是常数， ${\mu }_k$ 表示标准正态分布的k阶矩。

命题3. 设 $X_1,X_2,\cdots ,X_n$ 是来自PET的简单样本，其样本观测值为 $x_1,x_2,\cdots ,x_n$，则参数 $d_1$， $d_2$ 和 $d_3$ 的对数似然函数为

$\begin{array}{c}l=\ln L\left(d_1,d_2,d_3;x_1,x_2,\cdots ,x_n\right)\\ =-n\ln \left(1+3!d_1^2+4!d_2^2+6!d_3^2\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\ln }\left(1+d_1^2{H}_3^2\left(x_i\right)+d_2^2{H}_4^2\left(x_i\right)+d_3^2{H}_6^2\left(x_i\right)\right)\\ -\frac{n}{2}\ln 2\pi -\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i^2},\end{array}$

对数似然方程组

$\frac{\partial l}{\partial d_1}=\frac{-12n{d}_1}{\xi }+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{2d_1{H}_3^2\left(x_i\right)}{1+d_1^2{H}_3^2\left(x_i\right)+d_2^2{H}_4^2\left(x_i\right)+d_3^2{H}_6^2\left(x_i\right)}}=0,$

$\frac{\partial l}{\partial d_2}=\frac{-48n{d}_2}{\xi }+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{2d_2{H}_4^2\left(x_i\right)}{1+d_1^2{H}_3^2\left(x_i\right)+d_2^2{H}_4^2\left(x_i\right)+d_3^2{H}_6^2\left(x_i\right)}}=0,$

$\frac{\partial l}{\partial d_3}=\frac{-1440n{d}_3}{\xi }+{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{2d_3{H}_6^2\left(x_i\right)}{1+d_1^2{H}_3^2\left(x_i\right)+d_2^2{H}_4^2\left(x_i\right)+d_3^2{H}_6^2\left(x_i\right)}}=0.$

上式对数似然方程无解析解，借助R软件的DEoptim函数可以给出 $d_1$， $d_2$， $d_3$ 的最大似然估计值数值解。

3. APARCH-PET模型

本文提出APARCH-PET模型，具体表达式如下

$\{\begin{array}{l}{r}_t={\mu }_t+a_t,\\ a_t={\sigma }_t{\epsilon }_t,{\epsilon }_t~\text{PET},\\ {\sigma }_t^{\delta }=\omega +{\displaystyle \underset{i=0}{\overset{m}{\sum }}{\alpha }_i}{\left(\left|a_{t-1}\right|+{\gamma }_i{a}_{t-1}\right)}^{\delta }+{\displaystyle \underset{j=0}{\overset{s}{\sum }}{\beta }_j}{\sigma }_{t-1}^{\delta }.\end{array}$ (3)

其中， ${\mu }_t$， ${\sigma }_t$ 分别为 $r_t$ 的条件均值和条件标准差， $\delta >0$。 ${\epsilon }_t$ 服从均值为0，方差为1的PET分布。

由于PET分布包含偏度与峰度两个参数，APARCH模型能捕捉到收益率序列的非对称性，上式模型假定 ${\epsilon }_t$ 服从PET分布，提出的APARCH-PET模型兼具PET分布和APARCH模型的优良特性。一定程度上，本文提出的新模型具有灵活性和双重性。

由(3)及VaR平移不变性和正齐次性得

${\text{VaR}}_{1-\alpha }\left(r_t\right)={\mu }_t+{\sigma }_t{\text{VaR}}_{1-\alpha }\left({\epsilon }_t\right).$ (4)

其中， ${\text{VaR}}_{1-\alpha }\left({\epsilon }_t\right)$ 为PET的 $1-\alpha$ 分位数。

4. 模型应用

4.1. 拟合结果

本文选取上证主板招商银行股票日收盘价 $P_t$ 作为样本(数据来源：http://www.resset.cn/锐思金融数据库，时间区间为2007.01.04~2022.10.20)，共3810个数据。放大100倍的日对数收益率 $r_t=100\ln \left(P_t/P_{t-1}\right)$。

Table 1. Summary statistics of China Merchants Bank’s stock yield series

表1. 招商银行股票收益率序列概要统计量

注：ADF为ADF检验统计量。

从表1可以看出，偏度值为−0.1276，该序列存在左偏特征；峰度值为8.0419大于3，该序列比正态分布陡峭。同时，J-B统计检验在5%的显著性水平下，拒绝服从标准正态分布的原假设，数据存在尖峰厚尾特征。ADF的检验结果表明 $r_t$ 是平稳的序列。

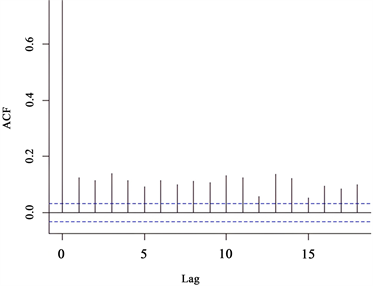
图2中招商银行日对数收益率的样本ACF均在两倍标准差之内，而平方后的样本ACF均超出两倍标准差，表明 $r_t$ 存在显著的ARCH效应，而APARCH模型恰能刻画此效应，所以用三种模型APARCH-PET，APARCH-PES，APARCH-norm来拟合 $r_t$。模型参数结果如表2。

(a) $r_t$ (b) $r_t^2$

Figure 2. $r_t$ with $r_t^2$ ACF diagram

图2. $r_t$ 与 $r_t^2$ 的ACF图

Table 2. APARCH model estimation results

表2. APARCH模型估计结果

根据表2可知，APARCH-PET模型的AIC与BIC均小于经典模型，这表明对于存在非称现象和具有尖峰厚尾特征的序列，用APARCH-PET模型拟合能达到更好的效果。

4.2. 返回测试

本文选取Kupiec [14] 失败率检验法评价APARCH-PET模型估算 ${\text{VaR}}_{1-\alpha }$ 值的优劣。定义示性函数

$I=\{\begin{array}{l}1,r_t>{\text{VaR}}_{1-\alpha },\\ 0,r_t\le {\text{VaR}}_{1-\alpha }.\end{array}$ (5)

令 $N=\#\left\{1\le t\le T:r_t>{\text{VaR}}_{1-\alpha }\right\}$ 表示收益率超过VaR值的总天数，T为序列总观测天数， ${\alpha }_0=N/T$ 表示失败频率，考虑原假设 $H_0:\alpha ={\alpha }_0$。则

$\text{LR}=2\ln \left[{\left(1-\frac{N}{T}\right)}^{T-N}{\left(\frac{N}{T}\right)}^N\right]-2\ln \left[{\left(1-{\alpha }_0\right)}^{T-N}{\alpha }_0^N\right].$

在原假设条件下，似然比统计量渐近服从 ${\mathcal{X}}^2\left(1\right)$ 分布，若 $\mathbb{P}\left({\mathcal{X}}^2\left(1\right)\ge \text{LR}\right)<0.05$，则认为模型无效，反之有效。计算2021.07.25~2022.10.20共300天数据的 ${\text{VaR}}_{1-\alpha }$，并对其结果进行失败率返回测试。

Table 3. VaR 1 − α Returns test results

表3. ${\text{VaR}}_{1-\alpha }$ 返回测试结果

表3给出残差序列分别采用PET和正态分布估算出的 ${\text{VaR}}_{1-\alpha }$ 返回测试结果。当 $1-\alpha =95\%$ 时，两种方法得到的p值均大于0.05通过检验，但当 $1-\alpha =99\%$ 时，正态分布拟合的残差序列估算出的值未通过检验。表3可知采用正态分布拟合残差序列的模型往往低估了金融风险，而采用PET分布拟合残差序列的模型在度量金融风险上更准确。

5. 结论

本文提出的PET分布包含了数据的峰度与偏度，在拟合尾部较厚的数据上比正态分布更合适，能更有效的拟合资产收益率数据“尖峰厚尾”特征。在APARCH模型的基础上，结合PET分布构建APARCH-PET模型，并选取上证主板招商银行股票数据进行实证分析。结果显示，用PET分布拟合残差序列的模型对VaR度量效果明显优于经典模型，新模型提高了估计VaR的精准度。对于存在非对称效应和尖峰厚尾特征的资产收益率数据，在度量金融风险时可以考虑利用APARCH-PET模型估算VaR值的方法，投资者可以进行更好的资金控制和风险管理。

基金项目

重庆市自然科学基金项目(cstc2020jcyj-msxmX0232)，重庆市高等教育教学改革研究项目(203332)，重庆市研究生科研创新项目(CYS21475)。

附录

证明命题1

$\begin{array}{c}F\left(x\right)=\mathbb{P}\left(X\le x\right)\\ ={\displaystyle {\int }_{-\infty }^x\frac{1}{\xi }}\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x\\ =\frac{1}{\xi }\left[{\displaystyle {\int }_{-\infty }^x\varphi }\left(x\right)\text{d}x+{\displaystyle {\int }_{-\infty }^x{d}_1^2}{H}_3^2\left(x\right)\varphi \left(x\right)\text{d}x+{\displaystyle {\int }_{-\infty }^x{d}_2^2}{H}_4^2\left(x\right)\varphi \left(x\right)\text{d}x+{\displaystyle {\int }_{-\infty }^x{d}_3^2}{H}_6^2\left(x\right)\varphi \left(x\right)\text{d}x\right]\end{array}$

根据Hermit多项式的性质可以计算出

$\begin{array}{c}F\left(x\right)=\mathbb{P}\left(X\le x\right)\\ =\frac{1}{\xi }[\left(1+3!d_1^2+4!d_2^2+6!d_3^2\right)\Phi \left(x\right)-{\displaystyle \underset{i=0}{\overset{2}{\sum }}\frac{3!d_1^2}{\left(3-i\right)!}{H}_{3-i}\left(x\right)H_{2-i}\left(x\right)\varphi \left(x\right)}\\ -{\displaystyle \underset{i=0}{\overset{3}{\sum }}\frac{4!d_2^2}{\left(4-i\right)!}{H}_{4-i}\left(x\right)H_{3-i}\left(x\right)\varphi \left(x\right)}-{\displaystyle \underset{i=0}{\overset{5}{\sum }}\frac{6!d_3^2}{(6-i)!}{H}_{6-i}\left(x\right)H_{5-i}\left(x\right)\varphi \left(x\right)}]\end{array}$

其中

$\begin{array}{c}\xi ={\displaystyle {\int }_{-\infty }^{\infty }\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x}\\ ={\displaystyle {\int }_{-\infty }^{\infty }\varphi }\left(x\right)\text{d}x+{\displaystyle {\int }_{-\infty }^{\infty }{d}_1^2}\left(9x^2-6x^4+x^6\right)\varphi \left(x\right)\text{d}x+{\displaystyle {\int }_{-\infty }^{\infty }{d}_2^2}\left(x^8-12x^6+42x^4-36x^2+9\right)\varphi \left(x\right)\text{d}x\\ +{\displaystyle {\int }_{-\infty }^{\infty }{d}_3^2}\left(x^{12}-30x^{10}+315x^8-705x^6+2250x^4-1350705x^2+225\right)\varphi \left(x\right)\text{d}x\\ =1+3!d_1^2+4!d_2^2+6!d_3^2\end{array}$

证明命题2

当k为偶数时，

$\begin{array}{c}{m}_k=\mathbb{E}\left(X^k\right)\\ ={\displaystyle {\int }_{-\infty }^{\infty }\frac{x^k}{\xi }}\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x\\ ={\displaystyle {\int }_{-\infty }^{\infty }\frac{{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)}{\xi }}\left(1+d_1^2{H}_3^2\left(x\right)+d_2^2{H}_4^2\left(x\right)+d_3^2{H}_6^2\left(x\right)\right)\varphi \left(x\right)\text{d}x\\ ={\displaystyle {\int }_{-\infty }^{\infty }\frac{\varphi \left(x\right)}{\xi }}\left[{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)+d_1^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_3^2\left(x\right)+d_2^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_4^2\left(x\right)+d_3^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_6^2\left(x\right)\right]\text{d}x\\ ={\displaystyle {\int }_{-\infty }^{\infty }\frac{\varphi \left(x\right)}{\xi }}\left[x^k+d_1^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_3^2\left(x\right)+d_2^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_4^2\left(x\right)+d_3^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}{H}_i^2\left(x\right)H_6^2\left(x\right)\right]\text{d}x\\ =\frac{1}{\xi }\left({\mu }_k+d_1^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_{i}3!i!}+d_2^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_{i}4!i!}+d_3^2{\displaystyle \underset{i=0}{\overset{\frac{k}{2}}{\sum }}{c}_i}6!i!\right)\end{array}$

NOTES

^*通讯作者。