无圈反向超图中Min-Max不相交反向超路算法设计

Design of Min-Max Disjoint Backward Hy-perpaths Algorithm in Acyclic Backward Hypergraph

摘要: 超图与反向超图是计算机网络和通信网络采用的一类重要的网络拓扑结构，为提高网络以及传输路径容错性，不相交路径设计与优化成为重要的研究课题。本文在有向无圈的反向超图中，当每一条反向超弧的尾节点数不超过给定常数λ时，对构建源点与汇点间两条点不相交反向超路(B超路)的Min-Max优化问题进行研究，使得两条反向超路中权值较大者的值能够达到全局最小。为解决该问题，首先构造并设计了基于原图的辅助图，该辅助图也是有向无圈的反向超图，并将原问题转化为辅助图的多权值函数B超路优化问题。从而设计了伪多项式算法得到该问题的最优解。基于该算法，进一步给出了近似算法的设计方案得到(1+ε)近似解，从而有效降低了计算复杂性。

Abstract: Hypergraph and backward hypergraph are an important class of the network topology used in computer networks and communication networks. In order to improve the fault tolerance of net-works and transmission paths, the design and optimization of disjoint paths have become im-portant research topics. In this paper, in the directional acyclic backward hypergraph, when the tail node number of each backward hyperarc does not exceed the given constant λ , the Min-Max opti-mization problem of constructing two node-disjoint backward hyperpaths (B-hyperpaths) from the source node to the sink node is researched, so that the value of the greater weight in this two node-disjoint backward hyperpaths can reach the global minimum. In order to solve this problem, the auxiliary hypergraph based on the original hypergraph is constructed and designed firstly, which is also a directional acyclic backward hypergraph. The original problem is transformed into a B-hyperpath optimization problem with multi-weight function in the auxiliary hypergraph. Thus a pseudo-polynomial algorithm is designed to obtain an optimal solution to the problem. Based on this algorithm, the design scheme of the approximation algorithm is further given to obtain an (1+ε) approximate solution which effectively reduce the complexity of calculation.

1. 引言

网络中基于特定优化目标的路径设计广泛应用于许多研究领域，并主要采用赋权图构建网络拓扑结构以及问题优化模型。文献 [1] 在有向赋权图中设计了多目标路径搜索方式。在网络中，为了保证传输路径的容错性，多路径设计具有非常重要的意义。以无线传感网络为背景，文献 [2] 设计了智能优化算法构建源节点到目标节点的k条不相交路径。在交通网络中，如果在确定的运输点之间想要找到多条节点不相交的路径，那么当个别路径故障之后依然能保持交通网络的连通性。文献 [3] 研究了在有向无圈图和3连通平面图中寻找两条不相交路径问题并给出有效算法。其中对不相交路径性能的优化目标也是多样化的，比如选择的不交路径满足所有路径中最长的路径权值尽可能小，这类问题就是寻找Min-Max不相交路径。文献 [4] 在有向无圈图中设计出寻找两条不相交路径的近似算法，问题的解决引用了文献 [3] 的PSA算法构建一般图的辅助图模型，在该模型下总共考虑了四种优化目标，分别为MinMax，Balanced，MinSum-MinMin和MinSum-MinMax。在一般图中，Balanced优化目标下寻找节点不相交路径问题和边不相交路径问题是NP完全的。并且Shiloach [3] 等人已经证明在一般图上寻找Min-Max优化目标的节点不相交路径问题是NP完全的，在有向无圈图上，该问题具有伪多项式时间算法。Fleischer [4] 等人给出了在有向无圈图上寻找Min-Max优化目标下节点不相交路径问题的 $\left(1+\epsilon \right)$ 近似算法。

然而在复杂的交通运输、网络设计和数据库系统等研究领域，一般图模型已经满足不了路径设计的需求，因此基于超图模型的超路径设计也被进一步研究。

超图模型在1966年首次被Berge提出 [5] ，超图的超边是包含两个及两个以上点的集合。超图模型被应用于公共交通领域 [6] [7] 、数据挖掘领域，比如对于知识图谱的关联规则的挖掘算法就是利用有向超图构建关联规则去发现知识短缺 [8] 。对于超图的路径优化问题现已设计出一些算法，比如最短超路搜索算法 [9] [10] [11] 、动态最短超路搜索算法 [12] 。关于超图中不相交超路的研究，文献 [13] 将超图的连通性与多路径设计问题联系起来并给出了超图中的Menger定理。

有向超图中的超边也叫作超弧，由尾节点集和头节点集两个节点集组成，方向从尾节点集指向头节点集，若超弧的头节点个数均为1时就称该有向超图为反向超图。文献 [14] 给出了反向超路的定义并设计了最短反向超树搜索算法。反向超路模型也逐渐被应用于通信网络、分子生物等科学研究领域 [15] 。本文考虑节点不相交超路径并提出了在无圈反向超图中寻找满足Min-Max优化目标的两条点不相交反向超路问题，其中边赋权函数值为正整数。

本文首先构造了辅助反向超图模型，将二元点对作为辅助图中新的节点，基于反向超弧和不相交反向超路的结构特点定义辅助图中的节点关联函数使得在原反向超图中求Min-Max两条不相交反向超路问题转化为在辅助图上利用标签集寻找满足一定条件的同源反向超路，并给出具有伪多项式时间的精确算法。最后通过压缩标签集的容量，给出 $1+\epsilon$ 近似算法。在得到有效解的同时降低了计算复杂度。

2. 概念与问题

2.1. 超图相关概念

超图 $\mathcal{H}=\left(\mathcal{V},\mathcal{E}\right)$ 是由点集 $\mathcal{V}$ 和超边集 $\mathcal{E}$ 组成，其中每一条超边包含两个及两个以上节点的集合。有向超图由点集和有向超边集组成，有向超边就是将一条超边的节点集合分成尾节点集 $T\left(E\right)$ 和头节点集 $H\left(E\right)$ ，方向从尾节点集指向头节点集，也称为超弧。超弧E也被写作 $\left(T\left(E\right),H\left(E\right)\right)$ 。当 $H\left(E\right)$ 中只有一个点时，超弧E也叫做反向弧。若有向超图中的弧均为反向弧，那么也称为反向超图。在 $\mathcal{H}$ 中，所有以节点v为头节点的反向弧的集合记作 $BS\left(v\right)$ ，该集合中的每一条弧称为点v的后向弧。

超路是超图中的一个点边集序列，从s到t的一条超路表示为 $P_{s,t}=\left(v_1=s,E_{i_1},v_2,\cdots ,E_{i_q},v_{q+1}=t\right)$ ， $s\in T\left(E_{i_1}\right)$ ， $t\in H\left(E_{i_q}\right)$ ， $v_j\in H\left(E_{i_{j-1}}\right)\cap T\left(E_{i_j}\right)$ ， $j=2,\cdots ,q$ 。如果 $t\in T\left(E_{i_1}\right)$ ，则 $P_{s,t}$ 是一个圈 [3] 。

在反向超图 $\mathcal{H}$ 中，反向超路(B超路) $P_{s,t}$ 是从s到t使用最少的反向弧使得 $P_{s,t}$ 上的每一点x都有从s到x的简单无圈超路。

在赋权反向超图中，每条超弧E都有权值 $W\left(E\right)$ 。给定一条反向超路 $P_{s,t}$ 的权值计算方式：假设沿着路 $P_{s,t}$ 到达点v的子路记作 $P_{s,t}\left(s\to v\right)$ ，则

$W\left(P_{s,s}\right)=0$

$W\left(P_{s,t}\left(s\to v\right)\right)=W\left(E\right)+\max \left\{W\left(P_{s,t}\left(s\to v_i\right)\right)\right\}$

$v_i\in T\left(E\right),E\in BS\left(v\right)\cap \mathcal{E}\left(P_{s,t}\right)$ 。

特别地，当反向弧的权值均为1时，路权记作路的长度 $L\left(P_{s,t}\right)$ 。

2.2. Min-Max不相交反向超路问题

Min-Max不相交反向超路问题：在反向超图 $\mathcal{H}=\left(\mathcal{V},\mathcal{E},W\right)$ 中，每条反向超弧的权值均取正整数，给定两个节点 $s,t\in \mathcal{V}$ ，寻找从s到t的两条节点不相交反向超路 $P_1,P_2$ 使得两条路的最大权值能够达到最小。

目标函数： $\min \left\{\max \left\{W\left(P_1\right),W\left(P_2\right)\right\}\right\}$ ，其中 $W\left(P_i\right)$ 是反向超路 $P_i$ 的路权。

3. 辅助超图模型

给定有向无圈反向超图 $\mathcal{H}=\left(\mathcal{V},\mathcal{E},W\right)$ ，权值 $\mathcal{H}=\left(\mathcal{V},\mathcal{E},W\right)$ 取正整数。给定源节点s和目标节点t，为了寻找从s到t的不交反向超路，把s记作 $v_1$ ，把t记作 $v_n$ ，按照弧的方向将节点从小到大排序，序号大的节点不存在弧指向序号小的节点。因为 $\mathcal{H}$ 无圈，从t出发的反向弧不会再回到t，所以把从t出发的反向弧均删去成为新 $\mathcal{H}$ 。根据新 $\mathcal{H}$ 构建辅助超图 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ ，令

$\begin{array}{l}{\mathcal{V}}_2=\left\{\langle i,j\rangle |1\le i,j\le n,i\ne j\right\}\cup \left\{\langle s,s\rangle ,\langle t,t\rangle \right\}\\ {\mathcal{E}}_2=\left\{\left(\left\{\langle i,j_l\rangle \right\},\langle i,k\rangle \right)|\left(\left\{v_{j_l}\right\},v_k\right)\in \mathcal{E},\min \left\{j_l\right\}\le i\right\}\\ \cup \left\{\left(\left\{\langle i_l,j\rangle \right\},\langle k,j\rangle \right)|\left(\left\{v_{i_l}\right\},v_k\right)\in \mathcal{E},\min \left\{i_l\right\}\le j\right\}\text{}\text{}\text{}\text{}\text{}\end{array}$

在 ${\mathcal{E}}_2$ 中，第一个集合中的超弧记作水平弧，第二个集合中的超弧记作纵向弧。图1 给出一个反向超图，其对应的辅助超图如图2。

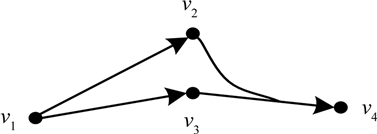
Figure 1. A backward acyclic hypergraph $\mathcal{H}$ with 4 nodes

图1. 节点个数为4的无圈反向超图 $\mathcal{H}$

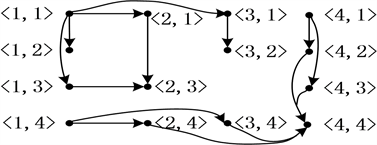
Figure 2. The auxiliary hypergraph of $\mathcal{H}$

图2. $\mathcal{H}$ 的辅助超图

定义1在 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ 中，若反向超路 $P\left(\langle s,s\rangle ,\langle t,t\rangle \right)$ 上的点满足：

· 对确定的i，从 $\langle s,s\rangle$ 沿着路P到达任意点 $\langle i,j\rangle$ 的子路上的纵向弧对应在 $\mathcal{E}$ 上的反向弧集合相同。

· 对确定的j，从 $\langle s,s\rangle$ 沿着路P到达任意点 $\langle i,j\rangle$ 的子路上的水平弧对应在 $\mathcal{E}$ 上的反向弧集合相同。

则 $P\left(\langle s,s\rangle ,\langle t,t\rangle \right)$ 是一条同源反向超路。

引理1在 $\mathcal{H}=\left(\mathcal{V},\mathcal{E}\right)$ 中，给定源节点s和图中任意两点 $t_1,t_2$ ，不相交反向超路 $P_{s,t_1},P_{s,t_2}$ 存在当且仅当在对应的辅助超图 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ 中存在同源反向超路 $P^2\left(\langle s,s\rangle \to \langle t_1,t_2\rangle \right)$ 。

证明：充分性：令 $P_1,P_2$ 是两条不交反向超路，对 $L\left(P_1\right)+L\left(P_2\right)$ 进行数学归纳。当 $L\left(P_1\right)+L\left(P_2\right)=2$ 时，两条节点不相交B超路分别为 $P_1=\left(s,t_1\right)$ ， $P_2=\left(s,t_2\right)$ ，在 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ 中 $P=\langle s,s\rangle \to \langle s,t_2\rangle \to \langle t_1,t_2\rangle$ 显然是同源反向超路。

当 $L\left(P_1\right)+L\left(P_2\right)>2$ ，假设当 $L\left(P_1\right)+L\left(P_2\right)<k$ 时，结论成立。记 $E_k=BS\left(t_1\right)\cap P_1$ ， $E_l=BS\left(t_2\right)\cap P_2$ 。不妨设 $T\left(E_k\right)$ 中顶点的下标的最小值小于 $T\left(E_l\right)$ 中顶点的下标的最小值，记 $T\left(E_l\right)=\left\{v_{x_1},v_{x_2},\cdots ,v_{x_m}\right\}$ 那么对每一个尾节点 $v_x$ 都满足 $L\left(P_1\right)+L\left(P_2\left(s\to v_{x_i}\right)\right)<L\left(P_1\right)+L\left(P_2\right)$ ，根据数学归纳法，在 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ 中存在从 $\langle s,s\rangle$ 到 $\langle t_1,v_{x_i}\rangle$ 的同源反向超路 $P_{x_i}^2$ 。然后令 $E^{\prime }=\left(\left\{\langle t_1,x_1\rangle ,\langle t_1,x_2\rangle ,\cdots ,\langle t_1,x_m\rangle \right\},\langle t_1,t_2\rangle \right)$ ，根据有向无圈超图中的节点序号的排列顺序，有 $\min \left\{x_1,x_2,\cdots ,x_m\right\}<\min \left\{t_1,t_2\right\}\le t_1$ ，故 $E^{\prime }\in \mathcal{E}\left({\mathcal{H}}^2\right)$ ，这样我们得到了一条反向超路 $P^2\left(\langle s,s\rangle \to \langle t_1,t_2\rangle \right)=E^{\prime }\cup \left(\cup P_{x_i}^2\right)$ ，因为在 ${\mathcal{H}}_2$ 对中，确定的 $t_2$ 只有一个节点 $\langle t_1,t_2\rangle$ ，根据数学归纳法， $P^2\left(\langle s,s\rangle \to \langle t_1,t_2\rangle \right)$ 上的水平弧对应在 $\mathcal{E}$ 上的反向弧集合是相同的。故该反向路是一条同源反向超路。

必要性：若同源反向超路 $P^2\left(\langle s,s\rangle \to \langle t_1,t_2\rangle \right)$ 存在，当 $L\left(P\right)=2$ ，将P中的水平弧对应在 $\mathcal{E}$ 中的反向弧放到 $\mathcal{E}\left(P_1\right)$ 中并删去冗余的反向弧即相同的反向弧，如 图2 中 $\left(\langle 3,1\rangle ,\langle 3,2\rangle \right)$ 和 $\left(\langle 4,1\rangle ,\langle 4,2\rangle \right)$ 对应在 $\mathcal{E}$ 中的反向弧为同一个 $\left(v_1,v_2\right)$ 。同样地，将P中的纵向弧对应在 $\mathcal{E}$ 中的反向弧放到 $\mathcal{E}\left(P_2\right)$ 中并删去冗余的反向弧，得到 $P_1=\left(s,t_1\right)$ ， $P_2=\left(s,t_2\right)$ ， $L\left(P_1\right)+L\left(P_2\right)=2$ 。

假设当 $L\left(P\right)<k$ 时，根据归纳假设结论成立，且有 $L\left(P_1\right)+L\left(P_2\right)=L\left(P^2\right)$ 。当 $L\left(P^2\right)=k$ 时，不妨设在该反向路的最后一条弧为 $E^{\prime }=\left(\left\{\langle t_1,x_1\rangle ,\langle t_1,x_2\rangle ,\cdots ,\langle t_1,x_m\rangle \right\},\langle t_1,t_2\rangle \right)$ 那么 $P^2$ 上的子路 $L\left(P^2\left(\langle s,s\rangle \to \langle t_1,x_i\rangle \right)\right)<L\left(P^2\right)$ ，根据上面 $P_1,P_2$ 的构造方式以及归纳假设，有 $P_1$ 和 $P_2\left(s\to v_{x_i}\right)$ 是两条不交B路。根据有向无圈B超图的节点排序规律，由于 $\min \left\{x_1,x_2,\cdots ,x_m\right\}<\min \left\{t_1,t_2\right\}\le t_2$ 。故节点 $t_2$ 也不在 $P_1$ 上，那么 $P_1,P_2$ 也是两条不相交反向超路。

例如在图2中，显然节点 $\langle 1,1\rangle$ 和 $\langle 4,4\rangle$ 不连通，这是由于在 $\mathcal{H}$ 中从 $v_1$ 到 $v_4$ 不存在两条不相交反向超路，故辅助超图中节点 $\langle 1,1\rangle$ 和 $\langle 4,4\rangle$ 不存在同源反向超路。

4. Min-Max不相交反向超路算法

基于上述辅助图的构造和定理，在原超图中找两条不相交反向超路问题可以转化为在辅助图中寻找同源反向超路问题。所以结合辅助超图给出算法去找从s到t的Min-Max节点不相交反向超路。该算法在限定反向弧的尾节点个数不超过常数 $\lambda$ 的反向超图上求解。为了记录辅助超图中同源反向超路分别对应的两条不交路的权值，每到达一个点就记录一个标签L存储两条路的权值和前继点，该标签方法在文献 [1] 中寻找一般图不相交路径被提出。到达点 $\langle i,j\rangle$ 的标签记为 $L_{i,j}\left(X,Y,pred\right)$ ，X和Y分别用来标记辅助图中到达点 $\langle i,j\rangle$ 的同源反向超路P对应到原图中两条不相交反向超路的权值，分别记作纵向权值和水平权值。值得注意的是这里的纵向权值(水平权值)并不是路P上纵向弧(水平弧)的权值的和，该值与第1节中反向超路的权值定义一致。Pred记录了路P上点 $\langle i,j\rangle$ 前继点和前继点的纵向权值和水平权值。节点 $\langle i,j\rangle$ 的所有标签均存储在 $I_{t,t}$ 中。算法1计算辅助图中每一个节点的标签集，当算法结束的时候，在 $\langle t,t\rangle$ 上的标签集中 $\max \left\{X,Y\right\}$ 达到最小的标签对应的同源反向超路就是最优Min-Max不相交反向超路对应的同源反向超路。算法2计算从 $\langle s,s\rangle$ 到 $\langle t,t\rangle$ 的最优同源反向超路，会用到算法1得到的目标节点 $\langle t,t\rangle$ 的标签集 $I_{t,t}$ 。算法3进行路径回溯，得到Min-Max不相交反向超路问题的最优解。

下面3小节分别给出这三个算法的具体步骤，并给出算法的正确性的证明和复杂度。

4.1. 计算标签集

给定反向超图 $\mathcal{H}$ ，利用第3节的模型构造得到辅助超图 ${\mathcal{H}}^2$ ，在辅助图上执行算法1计算每一个顶点的标签值 $\left(X,Y,pred\right)$ 。

首先初始化标签集合 $I_{i,j}=\varnothing ,1\le i,j\le n$ ，该集合包含点 $\langle i,j\rangle$ 的所有标签 $L_{i,j}$ ，同时令源节点的标签集为 $I_{1,1}=\left\{\left(0,0,NULL\right)\right\}$ 。接下来按照节点顺序计算每一个点的标签集，对每一个点 $\langle i,j\rangle$ 寻找它的后向弧即以它为头节点的反相弧并记作 $E^{\prime }$ 。把后向弧分成水平弧和纵向弧分别进行计算。

如果此刻考虑的后向弧是水平弧，接着判断该弧的尾节点的个数并记为 $\alpha$ ，将该弧的每一个尾节点 $\langle i,k_1\rangle ,\langle i,k_2\rangle ,\cdots ,\langle i,k_{\alpha }\rangle$ 的标签同时取出来一个比较纵向权值，因为根据同源反向超路的定义，到达这 $\alpha$ 个节点的纵向权值需要相同，即对应到原超图 $\mathcal{H}$ 上，到达节点i的反向超路是相同的，权值也一定相等。所以当判断条件 $X_1=X_2=\cdots =X_{\beta }$ 成立时，追溯两条纵向路是否相同，如果相同，那么就可以执行第11~13行去计算沿着弧 $E^{\prime }$ 到达点 $\langle i,j\rangle$ 的水平权值。首先记 $Y^{\prime }=\max \left\{Y_{k_{\beta }}\right\}$ ，再加 $E^{\prime }$ 的权值，令 $c=Y^{\prime }+W\left(\left\{v_{k_{\beta }}\right\},v_j\right)$

赋值给点 $\langle i,j\rangle$ 新标签的水平权值。根据B超路权值定义，为 $\langle i,j\rangle$ 计算新的标签值并放入 $I_{i,j}$ 中。如果节点的后向弧 $E^{\prime }$ 是纵向弧，那么尾节点就变成 $\langle k_1,j\rangle ,\langle k_2,j\rangle ,\cdots ,\langle k_{\alpha },j\rangle$ ，处理方法同上。

下面给出算法1的伪代码。

Algorithm 1. The calculation of the label set

算法1. 计算标签集

定理1. 在 ${\mathcal{H}}^2$ 中，对任意点 $\langle i,j\rangle$ ，如果存在从 $\langle s,s\rangle$ 到 $\langle i,j\rangle$ 的同源反向超路P，令 $X=W\left(P_V\right)$ ， $Y=W\left(P_H\right)$ ，当算法结束时，存在 $\left(X,Y,pred\right)\in I_{i,j}$ 且 $I_{i,j}$ 中仅包含同源反向超路对应的标签。

证明：对 $i+j$ 数学归纳，当 $i+j=2$ 时， $i=j=1$ ，在初始化步骤中算法设置了 $I_{1,1}=\left\{\left(0,0,NULL\right)\right\}$ 。假设 $i+j<k$ 时结论成立。当 $i+j=k$ 时，若路P上的最后一条反向弧的尾节点为 $\alpha$ ，不妨设最后一条反向弧为 $E^{\prime }=\left(\left\{\langle i,x_{\beta }\rangle \right\},\langle i,j\rangle \right)$ ，沿着路P从 $\langle s,s\rangle$ 到 $\langle i,x_{\beta }\rangle$ 的反向超路记为 $P^{x_{\beta }}$ ，并且记 $W\left(P_V^{x_{\beta }}\right)=X^{\beta +}$ ， $W\left(P_H^{x_{\beta }}\right)=Y^{\beta +}$ ，根据超路权值计算方式得到 $X=X^{\beta +}$ ， $Y=\max \left\{Y^{\beta +}|\beta =1,2,\cdots ,\alpha \right\}+W\left(E^{\prime }\right)$ 。因为 $x_{\beta }<j$ ， $i+x_{\beta }<i+j=k$ ，由归纳得 $\left(X^{\beta +},Y^{\beta +},pred\right)\in I_{i,x_{\beta }}$ 。若满足第10行的条件 $P_1^{x_1}=P_1^{x_2}=\cdots =P_1^{x_{\alpha }}$ ，执行第11~13行，得到新的标签 $\left(X,Y,T\left(E^{\prime }\right),\left\{\left(X,Y^{\beta +}\right)\right\}\right)$ 并存入 $I_{i,j}$ 中，根据第2节反向超路权值的计算方式可得 $X=W\left(P_V\right),Y=W\left(P_H\right)$ 。所以 $I_{i,j}$ 中存在 $\left(X,Y,pred\right)$ 。

还需证明 $I_{i,j}$ 中仅包含同源有向B路对应的标签。反证法：假设 $I_{i,j}$ 存在 $\left(X,Y,pred\right)$ 对应了一条非同源有向B超路P，则在P上至少存在两个点 $\langle x,y_1\rangle ,\langle x,y_2\rangle$ (或 $\langle x_1,y\rangle ,\langle x_2,y\rangle$ )沿着路P到达这两点的纵向弧(或水平弧)不相同，不妨设为 $\langle x,y_1\rangle ,\langle x,y_2\rangle$ ，沿着路P到达这两点的纵向路分别记作 $P_x^{y_1},P_x^{y_2}$ ，根据第12行的判断条件，由于 $P_x^{y_1}\ne P_x^{y_2}$ 并不会执行后面建立新标签的步骤，故不会放到 $I_{i,j}$ 中，矛盾。

复杂度：第3~4行需要 $n^2$ 次循环，第5行寻找后向边最多为m条边，第7行的循环次数为 $\left|I_{i,k_1}\right|\left|I_{i,k_2}\right|\cdots \left|I_{i,k_{\alpha }}\right|$ ，最多不超过 ${\left|I\right|}^{\lambda }$ 。第9行的路径回溯需要 $O\left(n\right)$ 的复杂度，所以算法1的复杂度为 $O\left(n^{3}m{\left|I\right|}^{\lambda }\right)$ ，其中 $\left|I\right|$ $\left|I\right|=n^2{W^{\prime }}^2$ 是标签集的最大容量， $W^{\prime }$ 为权值的最大值。

4.2. Min-Max不相交反向超路算法

算法2为Min-Max不相交反向超路算法，该算法为主算法。首先调用算法1得到节点 $\langle t,t\rangle$ 的标签集 $I_{t,t}$ 。其次对 $I_{t,t}$ 中每一个标签的水平权值和纵向权值的最大值即 $\max \left\{X,Y\right\}$ 进行比较，如 $\max \left\{X,Y\right\}$ 若较小就赋给 $\left(X^{*},Y^{*},pred\right)$ ，最终得到的 $\left(X^{*},Y^{*},pred\right)$ 就是最优解 $\min \left(\max \left\{X,Y\right\}\right)$ 。最后调用算法3得到 $\left(X^{*},Y^{*},pred\right)$ 对应的两条不相交反向超路 $P_1,P_2$ 。

下面给出算法2的具体步骤：

Algorithm 2. Min-Max disjoint backward hyperpaths algorithm

算法2. Min-Max不相交反向超路

定理2：算法2输出的 $P_1,P_2$ 是最优解。

证明：假设最优解为 $P_1^{\ast },P_2^{\ast }$ ，权值分别为 $W\left(P_1^{\ast }\right)$ 和 $W\left(P_2^{\ast }\right)$ 。根据引理1，在 ${\mathcal{H}}_2=\left({\mathcal{V}}_2,{\mathcal{E}}_2\right)$ 中存在同源反向超路 $P^{*}$ 与之对应。令 $X^{\prime }=W\left(P_V^{\ast }\right)=W\left(P_1^{\ast }\right),Y^{\prime }=W\left(P_H^{\ast }\right)=W\left(P_2^{\ast }\right)$ ，根据算法1的正确性， $\left(X^{\prime },Y^{\prime },pred\right)\in I_{t,t}$ 。若算法2没有输出最优解 $P^{*}$ 对应的标签 $\left(X\text{'},Y\text{'},pred\right)$ ，假设输出了另外一条同源反向路 $P^{\prime }$ 对应的标签 $\left(X,Y,pred\right)$ ，算法中对标签进行比较后选较小者，所以 $\max \left\{X,Y\right\}<\max \left\{X^{\prime },Y^{\prime }\right\}$ 。由于 $P^{*}$ 是最优解，那么一定有 $\max \left\{X,Y\right\}\ge \max \left\{X^{\prime },Y^{\prime }\right\}$ ，得出矛盾。故算法2输出的 $P_1,P_2$ 是Min-Max不相交反向超路的最优解。

复杂度：执行算法1需要 $O\left(n^{3}m{\left|I\right|}^{\lambda }\right)$ ，对 $I_{t,t}$ 中的每一个标签比较，复杂度为 $O\left(\left|I\right|\right)$ ，最后路径回溯复杂度为 $O\left(n\right)$ ，以上三个过程没有嵌套关系，故算法2的复杂度为 $O\left(n^{3}m{\left|I\right|}^{\lambda }\right)$ ，其中 $\left|I\right|$ 为标签集的最大容量， $\left|I\right|=n^2{W^{\prime }}^2$ ， $W^{\prime }$ 为权值的最大值。

4.3. 标签回溯算法

标签回溯算法是算法1和算法2调用的子算法，利用标签集得到在 $\mathcal{H}$ 中对应的两条不交反向超路。首先输入已有的标签集、到达的节点 $\langle i_1,j_1\rangle$ 和标签 $L_{i_1,j_1}=\left(X,Y,\left\{i^{\prime },j^{\prime }\right\},\left\{X_{i^{\prime }}^{+},Y_{j^{\prime }}^{+}\right\}\right)$ 。现设定队列N满足先进先出原则，初始只有 $L_{i_1,j_1}$ 并将其出队。因为要回溯到源节点 $\langle s,s\rangle$ ，而 $I_{s,s}=\left\{\left(0,0,NULL\right)\right\}$ ，只要当出队标签的 $pred\ne NULL$ 说明需要继续回溯。根据前继点判断前继弧是水平弧还是纵向弧，如果是水平弧即 $i^{\prime }=i_1$ 就将 $\mathcal{H}$ 中的反向弧 $\left(\left\{j^{\prime }\right\},j_1\right)$ 加到 $\mathcal{E}\left(P_2\right)$ 中，如果是纵向弧即 $j^{\prime }=j_1$ 就将反向弧 $\left(\left\{i^{\prime }\right\},i_1\right)$ 加到 $\mathcal{E}\left(P_1\right)$ 中。为了从前继点继续追溯，将每一个 $L_{i^{\prime },j^{\prime }}=\left(X_{i^{\prime }}^{+},Y_{j^{\prime }}^{+},pred\right)$ 入队到N，返回循环直至N为空。下面给出算法步骤：

Algorithm 3. Label backtracking algorithm (BACK)

算法3. 标签回溯算法

复杂度：根据有向无圈图的排序原则，到达 $v_{i^{\prime }}$ 和 $v_{j^{\prime }}$ 的路上最多有 $i^{\prime }$ 和 $j^{\prime }$ 个点，回溯时最多有 $i^{\prime }+j^{\prime }+2$ 个点入队到N且最多仅入队1次，所以循环次数最多为 $i^{\prime }+j^{\prime }+2$ 次，计算复杂度为 $O\left(n\right)$ 。

5. 近似算法

基于上述求Min-Max不相交反向超路问题的最优解，本节通过对路径权值的近似，降低了算法1中每一个节点的标签数量，进而设计了 $1+\epsilon$ 近似算法降低了计算复杂性。

首先依照第3节构建辅助超图模型。其次，对每一个节点 $\langle i,j\rangle$ ，建立新标签集合 $I_{i,j}$ 并将其新标签记为 $L_{i,j}\left[a,b\right]=\left(X,Y,pred\right)$ ，其中 $a=\lfloor {\log }_{\delta }X\rfloor +1$ ， $b=\lfloor {\log }_{\delta }Y\rfloor +1$ ， $a,b\le \lfloor {\log }_{\delta }\left(n{W}^{\prime }\right)\rfloor +1$ ，并且令 $\delta ={\left(1+\epsilon \right)}^{\frac{1}{2n-2}}$ ，当 $\epsilon >0$ 时， $\delta >1$ 。接下来给出新标签计算算法，具体步骤如下。

在初始化过程中，令每一个节点 $\langle i,j\rangle$ 的新标签为 $L_{i,j}\left[a,b\right]=NULL$ ，接下来初始化源节点 $\langle 1,1\rangle$ 的新标签为 $L_{1,1}\left[1,1\right]=\left(0,0,NULL\right)$ 。

接下来改进算法1计算对各点的新标签。算法1中第3~5行循环条件不变，当遍历的反向弧为水平弧时，将第7行变为对 $I_{i,k_{\beta }}$ 中的每一个 $L_{i,k_{\beta }}\left[a,b\right]=\left(X_{\beta },Y_{k_{\beta }},pred\right)$ 进行比较，8~11行步骤不变，第12行替换为 $c=\lfloor {\log }_{\delta }\left(Y^{\prime }+W\left(E^{\prime }\right)\right)\rfloor +1$ 。当 $i=j=t$ 时，为了删除部分冗余的标签，如果 $L_{t,t}\left[a,c\right]=\varnothing$ ，执行第13行 $L_{i,j}\left[a,c\right]=\left(X_1,Y^{\prime }+W\left(E^{\prime }\right),T\left(E^{\prime }\right),\left\{\left(X_{\beta },Y_{k_{\beta }}\right)\right\}\right)$ 和 $I_{i,j}=I_{i,j}\cup \left\{L_{i,j}\left[a,c\right]\right\}$ ，否则不更新 $I_{i,j}$ 。当遍历的反向弧为纵向弧时，将第20行变为对 $I_{k_{\beta },j}$ 中每一个 $L_{k_{\beta },j}\left[a,b\right]=\left(X_{k_{\beta }},Y_{\beta },pred\right)$ 进行比较，21~24行步骤不变，第25行替换为 $c=\lfloor {\log }_{\delta }\left(X^{\prime }+W\left(E^{\prime }\right)\right)\rfloor +1$ 。如果 $i=j=t$ 时，为了删除部分冗余的标签，如果 $L_{t,t}\left[c,b\right]=\varnothing$ ，执行第26行 $L_{i,j}\left[c,b\right]=\left(X^{\prime }+W\left(E^{\prime }\right),Y_1,T\left(E^{\prime }\right),\left\{\left(X_{k_{\beta }},Y_{\beta }\right)\right\}\right)$ $I_{i,j}=I_{i,j}\cup \left\{L_{i,j}\left[c,b\right]\right\}$ ，否则不更新 $I_{i,j}$ 。

由于标签有了变化，通过执行上述算法，将反向超路的两个权值存储到了 $a,b\le \lfloor {\log }_{\delta }\left(n{W}^{\prime }\right)\rfloor +1$ 以内的新标签中，并且在 $I_{t,t}$ 内的标签由于压缩出现重复值，我们添加了 $L_{t,t}\left[c,b\right]=\varnothing$ 条件筛选出冗余的标签，执行算法4在 $I_{t,t}$ 中比较 $L_{t,t}\left[a,b\right]$ 存储的 $\left(X,Y,pred\right)$ ，得到近似解 $\left(X^{*},Y^{*},pred\right)$ 。具体步骤如下：

Algorithm 4. Approximation algorithm for Min-Max target

算法4. Min-Max目标近似算法

引理2：假设在 ${\mathcal{H}}_2$ 中存在一条从 $\langle s,s\rangle$ 到 $\langle i,j\rangle$ 同源有向B超路P，令 $X=W\left(P_V\right),Y=W\left(P_H\right)$ ，当近似算法结束时，节点 $\langle i,j\rangle$ 存在新标签 $L_{i,j}\left[a,b\right]=\left(X^{\prime },Y^{\prime },pred\right)\in {I^{\prime }}_{t,t}$ 使得 $X/{\delta }^{i+j-2}\le X^{\prime }\le {\delta }^{i+j-2}X$ ， $Y/{\delta }^{i+j-2}\le Y^{\prime }\le {\delta }^{i+j-2}Y$ 。

证明：对 $i+j$ 进行归纳，当 $i+j=2$ 时，由于初始化中在 $I_{1,1}$ 中只有 $\left(0,0\right)$ ，显然满足结论。当 $i+j<k$ 时，假设结论成立。令 $i+j=k$ ，假设在 ${\mathcal{H}}_2$ 中存在一条从 $\langle s,s\rangle$ 到 $\langle i,j\rangle$ 同源反向超路P，不妨假设超路P上点 $\langle i,j\rangle$ 的后向弧为 $E^{\prime }=\left(\left\{\langle i,x_{\beta }\rangle \right\},\langle i,j\rangle \right)$ ，沿着P到达点 $\langle i,x_{\beta }\rangle$ 的纵向权值和水平权值分别记为 $W\left(P_V^{x_{\beta }}\right)=X^{\beta +}$ ， $W\left(P_H^{x_{\beta }}\right)=Y^{\beta +}$ ，则可以得到 $X=X^{\beta +}$ ， $Y=\max \left\{Y^{\beta +}|\beta =1,2,\cdots ,\alpha \right\}+W\left(E^{\prime }\right)$ 。又因为 $x_{\beta }<j$ ，所以 $i+x_{\beta }<i+j=k$ ，由归纳假设，节点 $\langle i,x_{\beta }\rangle$ 的标签集中存在标签 $\left(X^{{\beta }^{\prime }},Y^{{\beta }^{\prime }},pred\right)$ 满足

$X^{\beta +}/{\delta }^{i+x_{\beta }-2}\le X^{{\beta }^{\prime }}\le {\delta }^{i+x_{\beta }-2}{X}^{\beta +}$

$Y^{\beta +}/{\delta }^{i+j-2}\le Y^{{\beta }^{\prime }}\le {\delta }^{i+j-2}{Y}^{\beta +}$

节点 $\langle i,j\rangle$ 的新标签为 $\left(X^{{\beta }^{\prime }},Y^{{\beta }^{\prime }}+W\left(E^{\prime }\right),\left\{\langle i,x_{\beta }\rangle \right\},\left\{X^{{\beta }^{\prime }},Y^{{\beta }^{\prime }}\right\}\right)$ 。令 $X^{\prime }=X^{{\beta }^{\prime }}$ 和 $Y^{\prime }=Y^{{\beta }^{\prime }}+W\left(E^{\prime }\right)$ ，得

$X^{\prime }=X^{{\beta }^{\prime }}\le {\delta }^{i+x_{\beta }-2}{X}^{\beta +}\le {\delta }^{i+j-2}X$ ，

$\begin{array}{c}{Y}^{\prime }=Y^{{\beta }^{\prime }}+W\left(E^{\prime }\right)\\ \le {\delta }^{i+x_{\beta }-2}{Y}^{\beta +}+W\left(E^{\prime }\right)\\ \le {\delta }^{i+x_{\beta }-2}\left(Y^{\beta +}+W\left(E^{\prime }\right)\right)\\ \le {\delta }^{i+x_{\beta }-2}Y\\ \le {\delta }^{i+j-2}Y\end{array}$

$X^{\prime }=X^{{\beta }^{\prime }}\ge X^{\beta +}/{\delta }^{i+x_{\beta }-2}\ge X/{\delta }^{i+j-2}$

由于 $\delta >1$ 所以

$\begin{array}{c}{Y}^{\prime }=Y^{{\beta }^{\prime }}+W\left(E^{\prime }\right)\\ \ge Y^{\beta +}/{\delta }^{i+x_{\beta }-2}+W\left(E^{\prime }\right)\\ \ge \left(Y^{\beta +}+W\left(E^{\prime }\right)\right)/{\delta }^{i+x_{\beta }-2}\\ \ge Y/{\delta }^{i+x_{\beta }-2}\\ \ge Y/{\delta }^{i+j-2}\end{array}$

定理3：Min-Max不相交反向超路近似算法得到 $1+\epsilon$ 近似解。

证明：假设从 $\langle 1,1\rangle$ 到 $\langle n,n\rangle$ 最优解为 $P_1^{*},P_2^{*}$ ，并且其对应的权值分别为 $X^{*},Y^{*}$ ，近似算法得到的解为 $\left(X,Y,pred\right)$ 。根据引理2，节点 $\langle n,n\rangle$ 存在标签 $L_{i,j}\left[a,b\right]=\left(X^{\prime },Y^{\prime },pred\right)\in {I^{\prime }}_{t,t}$ 使得 $X^{\prime }\le {\delta }^{2n-2}{X}^{*}$ 和 $Y^{\prime }\le {\delta }^{2n-2}{Y}^{*}$ 。因为 $\delta ={\left(1+\epsilon \right)}^{\frac{1}{2n-2}}$ ，所以 $X^{\prime }\le \left(1+\epsilon \right)X^{*}$ ， $Y^{\prime }\le \left(1+\epsilon \right)Y^{*}$ 。那么

$\begin{array}{c}\max \left\{X,Y\right\}\le \max \left\{X^{\prime },Y^{\prime }\right\}\\ \le \max \left\{\left(1+\epsilon \right)X^{*},\left(1+\epsilon \right)Y^{*}\right\}\\ =\left(1+\epsilon \right)\max \left\{X^{*},Y^{*}\right\}\end{array}$

因此，该不相交反向超路近似算法得到了 $1+\epsilon$ 近似解。

复杂度：Min-Max不相交反向超路近似算法的复杂度为 $O\left(n^{3}m{\left|I^{\prime }\right|}^{\lambda }\right)$ ，其中 $\left|I^{\prime }\right|={\left({\log }_{\delta }\left(n{W}^{\prime }\right)\right)}^2$ ， $W^{\prime }$ 为反向弧权值的最大值。该近似算法的复杂度计算过程与4.2节类似，在此不再赘述。

6. 结语

在本篇论文中，我们研究了在无圈反向超图中寻找固定源节点到目标节点间的两条点不相交反向超路的设计优化问题，采用Min-Max作为优化目标。通过建立辅助超图模型，将原反向超图的Min-Max不交超路问题转化为在辅助超图中找一条具有两个边权函数的同源反向超路优化问题。当给定反向弧尾节点个数的上限 $\lambda$ 时，给出算法1计算辅助超图中目标节点的标签，从而通过算法2获得了满足Min-Max目标的同源反

向超路，在算法2中调用算法3得到不相交反向超路问题的最优解。主算法的复杂度为 $O\left(n^{3}m{\left|I\right|}^{\lambda }\right)$ ，其中 $\left|I\right|=n^2{W^{\prime }}^2$ 。为进一步降低该伪多项式算法的计算复杂性，本文设计了复杂度为 $O\left(n^{3}m{\left|I^{\prime }\right|}^{\lambda }\right)$ 的 $\left(1+\epsilon \right)$ 近似算法，其中 $\left|I^{\prime }\right|={\left({\log }_{\delta }\left(n{W}^{\prime }\right)\right)}^2$ 。之后我们将继续在网络中多路径优化方面进行研究，包括Min-Sum和限制

Min-Sum等不同的优化目标。该研究可以应用到不同的场景和复杂网络当中，为提高网络和路径容错性提供解决方案。