Winkler/Pasternak/Kerr地基上多孔FG板基于四变量板理论的自由振动分析

A Novel Four-Variable Plate Theory for Free Vibration of FG Plates with Porosities Resting on Winkler/Pasternak/Kerr Foundation

摘要: 本文提出了一种新的广义四变量板理论，用于弹性地基上孔隙依赖功能梯度材料板(porous func-tionally gradedplate，简称孔隙依赖FG板)自由振动分析。考虑了三种不同的孔隙率分布(包括均匀分布、非均匀分布和对数非均匀分布)并对三种不同的地基(Winkler-Pasternak地基和Kerr地基)行了研究。通过哈密顿原理得到控制方程，通过解特征值问题得到了数值结果，研究了不同孔隙率、长细比、幂律指数和弹性刚度参数对多孔FG板基频的影响，并将所得的结果与已有文献进行对比，验证了本文理论的准确性。

Abstract: The free vibration responses of porous functionally graded plate(FG)rectangular plates resting on elastic foundations are investigated according to a novel four-variable refined plate theory. Three types of porosities distributions (even and uneven, and the logarithmic-uneven distribution) are learned. The elastic foundations are considered as Winkler-PasternakandKerr foundation. Governing equations are derived by using Hamilton principle. The effect of porosity parameter, slenderness ratio, the power-law index and parameters of elastic foundation are also investigated. The the-oretical calculation results of fundamental frequency of porous FG plates resting on elastic foundations are predicted by solving the eigenvalue problems and compared with the available results in the literature to verify the theory.

1. 引言

功能梯度材料(functionally graded，简称FG)是由两种或两种以上的组分组成的各向同性、微观不均匀的材料，材料特性在特定方向上连续平滑变化，它可以满足特定的机械设计要求，有着消去层间应力、分层破坏和热变形等优点，这些特性使功能梯度材料在航空航天、船舶、核能等领域发挥着重要作用。

由于FGM结构的广泛应用，评估它力学性能的研究有很多。Zhao等 [1] 利用FSDT和改进的傅立叶级数方法研究了具有弹性边界条件的FG多孔矩形板的自由振动问题。Nguyen等人 [2] 研究了反三角剪切变形理论下的功能梯度夹层板的静态、屈曲和自由振动问题。El Meiche等 [3] 提出了一种双曲剪切变形理论来进行FG夹层板屈曲和自由振动分析。Thai [4] [5] 使用四未知高阶剪切变形理论对FG板进行了弯曲和自由振动分析。Mantari等 [6] 提出了一种新的非多项式高阶剪切理论，用于分析Pasternak基础上FG板的振动。Mantari等 [7] 利用广义准三维混合剪切变形理论研究了FG板在Pasternak地基上的自由振动。Malekzadeh [8] 采用微分求积法和级数解研究了双参数弹性地基上FG矩形板的自由振动。Li等 [9] 研究了Winkler-Pasternak弹性地基上纤维增强夹层FG多孔板的非线性振动和动力屈曲。Baferani等 [10] 使用三阶剪切理论分析了在双参数弹性基础上的FG矩形板的力学行为。Yang等 [11] 基于一阶剪切变形梁理论分析了弹性地基上FG多层纳米复合梁的屈曲和后屈曲。Duc等 [12] 研究了基于Winkler-Pasternak弹性地基的FG碳纳米管增强复合材料板的静态和自由振动分析。Sheikholeslami和Saidi [13] 采用Batra和Vidoli提出的分析方法研究了简支FG矩形板在Winkler-Pasternak弹性地基上的自由振动。Thai和Choi [14] 使用了一种细化的板理论来分析基于双参数Pasternak基础的FG板的振动和屈曲。Mahmoudi等 [15] 报道了基于Pasternak弹性地基的夹层FG板的热力学行为。Demirhan [16] 等用Levy法研究了各种边界下的弹性地基上的FG板的弯曲和振动问题。Lü [17] 等人用空间状态法计算了弹性地基上厚FG板的精确基频。Li [18] 等用准三维理论计算了弹性地基上的FG板的自由振动问题。Phuong [19] 等计算了复合荷载下高阶剪切变形纤维FG石墨烯增强层合板的非线性屈曲。Wang [20] 等分析了一阶剪切变形理论框架下石墨烯增强复合材料层合板屈曲和自由振动的半解析解。Zenkour [21] 等研究了基于准三维理论的弹性地基上的多孔夹层FG板的弯曲。Hadji [22] 等分析了孔隙依赖FG夹层板的固有频率。

本文主要用四变量板理论，通过用弯曲w_b和剪切w_s横向位移来模拟剪切理论的横向位移w₀。该理论变量少计算简单，而且不需要考虑剪切修正因子。板的力学性能在厚度方向上随着幂律指数变化而变化。利用哈密顿原理，推导了基于弹性地基的孔隙依赖FG板的控制方程。然后通过Navier法来求解这些运动方程，通过求解特征值问题，得到了固有频率。通过与文献中已有解的比较，验证了本文的准确性。

2. 基本模型

2.1. 孔隙依赖FGM材料

考虑长度a宽度b和均匀厚度h的FG矩形板，其几何结构和坐标系如图1所示，假设其底面为金属顶面为陶瓷，其材料特性在厚度方向均匀变化。基于具有均匀孔隙率的混合律模型，FG板的材料参数可以写成厚度坐标z的函数表示如式(1)~(3)，角标c和m分别表示陶瓷和金属，P表示FG板的幂律指数，ζ表示FG板的物性参数(杨氏模量E、泊松比v和密度ρ)， ${\zeta }_c$ 和 ${\zeta }_m$ 分别表示陶瓷和金属的物性参数，ξ (0 < ξ ≤ 1)表示孔隙率。

(a) (b) (c)

Figure 1. The geometry of FG plate resting on (a) Winkler (b) Pasternak and (c) Kerr foundation

图1. 矩形FGM板嵌入(a) Winkler基础(b) Pasternak基础和(c) Kerr基础

2.1.1. 均匀模型

$\zeta \left(z\right)={\zeta }_c\left({\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\frac{\xi }{2}\right)+{\zeta }_m\left(1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\frac{\xi }{2}\right)$ (1)

2.1.2. 非均匀模型

$\zeta \left(z\right)={\zeta }_c\left({\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\frac{\xi }{2}\left(1-\frac{2\left|z\right|}{h}\right)\right)+{\zeta }_m\left(1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\frac{\xi }{2}\left(1-\frac{2\left|z\right|}{h}\right)\right)$ (2)

2.1.3. 对数非均匀模型

$\zeta \left(z\right)={\zeta }_c\left({\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\log \left(1+\frac{\xi }{2}\right)\left(1-\frac{2\left|z\right|}{h}\right)\right)+{\zeta }_m\left(1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^P-\log \left(1+\frac{\xi }{2}\right)\left(1-\frac{2\left|z\right|}{h}\right)\right)$ (3)

2.2. 弹性地基模型

2.2.1. Winkler模型

Winkler模型的载荷分布定义如下

$q_{Winkler}=K_w\left(w_b+w_s\right)$ (4)

其中 $K_w$ 是介质反应模量即弹簧的刚度系数。

2.2.2. Pasternak模型

Pasternak模型是一个双参数弹性模型，由刚度是 $G_p$ 的剪切层和刚度是 $K_w$ 的独立上弹簧组成， $G_p$ 表示弹簧部件之间的切向相互作用，因此，Pasternak模型与FG板之间的载荷分布可定义为

$q_{Pasternak}=K_w\left(w_b+w_s\right)+G_p{\nabla }^2\left(w_b+w_s\right)$ (5)

其中 ${\nabla }^2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$ 是笛卡尔坐标系下的拉普拉斯微分算子，当弹簧间相互作用 $G_p=0$ 时Pasternak可以退化为Winkler模型。

2.2.3. Kerr模型

Kerr地基模型是一个三参数弹性模型，由一个刚度为 $K_s$ 剪切层、刚度为 $K_u$ 的独立上弹簧层和刚度为 $K_l$ 独立的下弹簧层组成。Kerr模型的载荷分布定义如下 [23]

$q_{Kerr}=\frac{K_l{K}_u}{K_l+K_u}\left(w_b+w_s\right)-\frac{K_s{K}_u}{K_l+K_u}{\nabla }^2\left(w_b+w_s\right)$ (6)

2.3. 四变量板理论

四变量板理论的位移场定义为

$u=u_0-z\frac{\partial w_b}{\partial x}+f\left(z\right)\frac{\partial w_s}{\partial x},v=v_0-z\frac{\partial w_b}{\partial y}+f\left(z\right)\frac{\partial w_s}{\partial y},w=w_b+w_s$ (7)

其中u₀和v₀分别表示x和y方向的面内位移，横向位移w分为弯曲作用引起的 $w_b$ 和剪切作用引起的 $w_s$ ， $f\left(z\right)$ 是剪切形函数，本文用到的是一种新的多项式函数

$f\left(z\right)=0.1z-1.62z^3-\frac{16}{5h^4}\left(1-\frac{13.86h^2}{4}\right)z^5$ (8)

3. 基本方程

3.1. 本构关系

基于小变形假设，线性应变表示如下

$\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial u_0}{\partial x}\\ \frac{\partial v_0}{\partial y}\\ \frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}\end{array}\right\}+z\left\{\begin{array}{c}-\frac{{\partial }^2{w}_b}{\partial x^2}\\ -\frac{{\partial }^2{w}_b}{\partial y^2}\\ -2\frac{{\partial }^2{w}_b}{\partial x\partial y}\end{array}\right\}+f\left(z\right)\left\{\begin{array}{c}\frac{{\partial }^2{w}_s}{\partial x^2}\\ \frac{{\partial }^2{w}_s}{\partial y^2}\\ 2\frac{{\partial }^2{w}_s}{\partial x\partial y}\end{array}\right\},\left\{\begin{array}{c}{\gamma }_{xz}\\ {\gamma }_{yz}\end{array}\right\}=\left\{\begin{array}{c}\left(1+f^{\prime }\left(z\right)\right)\frac{\partial w_s}{\partial x}\\ \left(1+f^{\prime }\left(z\right)\right)\frac{\partial w_s}{\partial y}\end{array}\right\}$ (9)

广义胡克定律的应力应变关系为

$\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\tau }_{xy}\\ {\tau }_{xz}\\ {\tau }_{yz}\end{array}\right\}=\left\{\begin{array}{cccccc}{Q}_{11}& Q_{12}& Q_{13}& 0& 0& 0\\ Q_{21}& Q_{22}& Q_{23}& 0& 0& 0\\ Q_{31}& Q_{32}& Q_{33}& 0& 0& 0\\ 0& 0& 0& Q_{66}& 0& 0\\ 0& 0& 0& 0& Q_{44}& 0\\ 0& 0& 0& 0& 0& Q_{55}\end{array}\right\}\left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\gamma }_{xy}\\ {\gamma }_{xz}\\ {\gamma }_{yz}\end{array}\right\}$ (10)

其中应力为( ${\sigma }_{xx},{\sigma }_{yy},{\sigma }_{zz},{\tau }_{xy},{\tau }_{xz},{\tau }_{yz}$ )，应变为( ${\epsilon }_{xx},{\epsilon }_{yy},{\epsilon }_{zz},{\gamma }_{xy},{\gamma }_{xz},{\gamma }_{yz}$ )，在不考虑厚度拉伸效应时( ${\epsilon }_{zz}=0$ )弹性常数定义如下

$Q_{11}=Q_{22}=\frac{E\left(z\right)}{1-v{\left(z\right)}^2},Q_{12}=Q_{21}=\frac{v\left(z\right)E\left(z\right)}{1-v{\left(z\right)}^2},Q_{66}=Q_{44}=Q_{55}=\frac{E\left(z\right)}{2\left(1+v\left(z\right)\right)}$ (11)

应用哈密顿能量原理推导孔隙依赖FG板的运动方程

${\displaystyle \int \delta \left(U_S+V_E-K\right)\text{d}t}=0$ (12)

其中 $\delta$ 是变分符号， $U_S$ 分别表示应变能， $V_E$ 表示弹性地基势能，K表示FG板的动能。

3.2. 应变能

应变能变分为

$\begin{array}{c}\delta U_S={\displaystyle \underset{A}{\iint }{\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_{xx}\delta {\epsilon }_{xx}+{\sigma }_{yy}\delta {\epsilon }_{yy}+{\tau }_{xy}\delta {\gamma }_{xy}+{\tau }_{xz}\delta {\gamma }_{xz}+{\tau }_{yz}\delta {\gamma }_{yz}\right)\text{d}z\text{d}A}}\\ ={\displaystyle \underset{A}{\iint }[N_{xx}\delta \frac{\partial u_0}{\partial x}}-M_{xx}\delta \frac{{\partial }^2{w}_b}{\partial x^2}+S_{xx}\delta \frac{{\partial }^2{w}_s}{\partial x^2}+N_{yy}\delta \frac{\partial v_0}{\partial y}-M_{yy}\delta \frac{{\partial }^2{w}_b}{\partial y^2}+S_{yy}\delta \frac{{\partial }^2{w}_s}{\partial y^2}\\ +N_{xy}\left(\delta \frac{\partial u_0}{\partial y}+\delta \frac{\partial v_0}{\partial x}\right)-2M_{xy}\delta \frac{{\partial }^2{w}_b}{\partial x\partial y}+2S_{xy}\delta \frac{{\partial }^2{w}_s}{\partial x\partial y}+Q_x\delta \frac{\partial w_s}{\partial x}+Q_y\delta \frac{\partial w_s}{\partial y}]\text{d}A\end{array}$ (13)

其中

$\begin{array}{l}\left(N_{xx},N_{yy},N_{xy}\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_{xx}\text{,}{\sigma }_{xx},{\sigma }_{xx}\right)\text{d}z}\\ \left(M_{xx},M_{yy},M_{xy}\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_{xx}\text{,}{\sigma }_{xx},{\sigma }_{xx}\right)z\text{d}z}\\ \left(S_{xx},S_{yy},S_{xy}\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_{xx}\text{,}{\sigma }_{xx},{\sigma }_{xx}\right)f\left(z\right)\text{d}z}\\ \left(Q_x,Q_y\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\tau }_{xz},{\tau }_{yz}\right)\left(1+f^{\prime }\left(z\right)\right)\text{d}z}\end{array}$ (14)

$\left(A_{ij},B_{ij},C_{ij},D_{ij},H_{ij},F_{ij},K_{ij}\right)={\displaystyle {\int }_{z_k}^{z_{k+1}}{Q}_{ij}\left[1,z,f\left(z\right),z^2,zf\left(z\right),f^2\left(z\right),{\left(f^{\prime }\left(z\right)+1\right)}^2\right]\text{d}z}$ (15)

3.3. 弹性地基引起的势能

势能变分为

$\delta V_E=-{\displaystyle \underset{A}{\int }{\displaystyle \underset{-h/2}{\overset{h/2}{\int }}\left(q_{Winkler}+q_{Pasternak}+q_{Kerr}\right)\delta \left(w_b+w_s\right)\text{d}z\text{d}A}}$ (16)

3.4. 动能

动能变分为

$\begin{array}{c}\delta K={\displaystyle {\int }_0^a{\displaystyle {\int }_0^b{\displaystyle {\int }_{z_k}^{z_{k+1}}\rho \left(z\right)\left(\stackrel{\dot{}}{U}\delta \stackrel{\dot{}}{U}+\stackrel{\dot{}}{V}\delta \stackrel{\dot{}}{V}+\stackrel{\dot{}}{W}\delta \stackrel{\dot{}}{W}\right)\text{d}z\text{d}x\text{d}y}}}\\ ={\displaystyle {\int }_0^a{\displaystyle {\int }_0^b\{I_0\left[{\stackrel{\dot{}}{u}}_0\delta {\stackrel{\dot{}}{u}}_0+{\stackrel{\dot{}}{v}}_0\delta {\stackrel{\dot{}}{v}}_0+\left({\stackrel{\dot{}}{w}}_b+{\stackrel{\dot{}}{w}}_s\right)\delta \left({\stackrel{\dot{}}{w}}_b+{\stackrel{\dot{}}{w}}_s\right)\right]-I_1[\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}\delta {\stackrel{\dot{}}{u}}_0+{\stackrel{\dot{}}{v}}_0\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}+{\stackrel{\dot{}}{u}}_0\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}}}\\ +\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}\delta {\stackrel{\dot{}}{v}}_0]+I_2\left[\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}+\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}\right]+I_3\left[{\stackrel{\dot{}}{u}}_0\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}+{\stackrel{\dot{}}{v}}_0\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}+\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}\delta {\stackrel{\dot{}}{v}}_0+\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}\delta {\stackrel{\dot{}}{u}}_0\right]\\ -I_4\left[\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}+\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial x}+\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}\delta \frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}+\frac{\partial {\stackrel{\dot{}}{w}}_b}{\partial y}\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}\right]+I_5\left[\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial y}+\frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}\delta \frac{\partial {\stackrel{\dot{}}{w}}_s}{\partial x}\right]\}\text{d}A\end{array}$ (17)

位移变量上的点表示对时间求导，其中

$\left[I_0,I_1,I_2,I_3,I_4,I_5\right]={\displaystyle {\int }_{z_k}^{z_{k+1}}\rho \left(z\right)}\left[1,z,z^2,f\left(z\right),zf\left(z\right),f^2\left(z\right)\right]\text{d}z$ (18)

将应变能(13)、势能(16)和动能(17)带入式(12)，通过对各项积分，可以得到孔隙依赖FG板的运动方程：

$\begin{array}{l}\delta u_0:\frac{\partial N_{xx}}{\partial x}+\frac{\partial N_{xy}}{\partial y}=I_0{\ddot{u}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial x}-I_3\frac{\partial {\ddot{w}}_s}{\partial x}\\ \delta v_0:\frac{\partial N_{yy}}{\partial y}+\frac{\partial N_{xy}}{\partial x}=I_0{\ddot{v}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial y}-I_3\frac{\partial {\ddot{w}}_s}{\partial y}\\ \delta w_b:\frac{{\partial }^2{M}_{xx}}{\partial x^2}+\frac{{\partial }^2{M}_{yy}}{\partial y^2}+2\frac{{\partial }^2{M}_{xy}}{\partial x\partial y}-\left(q_{Winkler}+q_{Pasternak}+q_{Kerr}\right)\\ =-I_1\frac{\partial {\ddot{u}}_0}{\partial x}+I_2\frac{{\partial }^2{\ddot{w}}_b}{\partial x^2}-I_4\frac{{\partial }^2{\ddot{w}}_s}{\partial x^2}-I_1\frac{\partial {\ddot{v}}_0}{\partial y}+I_2\frac{{\partial }^2{\ddot{w}}_b}{\partial y^2}-I_4\frac{{\partial }^2{\ddot{w}}_s}{\partial y^2}+I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)\\ \delta w_s:\frac{{\partial }^2{S}_{xx}}{\partial x^2}+\frac{{\partial }^2{S}_{yy}}{\partial y^2}+2\frac{{\partial }^2{S}_{xy}}{\partial x\partial y}-\frac{\partial Q_x}{\partial x}-\frac{\partial Q_y}{\partial y}-\left(q_{Winkler}+q_{Pasternak}+q_{Kerr}\right)\\ =-I_3\frac{\partial {\ddot{u}}_0}{\partial x}+I_4\frac{{\partial }^2{\ddot{w}}_b}{\partial x^2}-I_5\frac{{\partial }^2{\ddot{w}}_s}{\partial x^2}-I_3\frac{\partial {\ddot{v}}_0}{\partial y}+I_4\frac{{\partial }^2{\ddot{w}}_b}{\partial y^2}-I_5\frac{{\partial }^2{\ddot{w}}_s}{\partial y^2}+I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)\end{array}$ (19)

4. 求解

本文利用纳维法定义偏微分方程组的解析解，基于如下重三角函数来假设满足边界条件。

其中： ${\lambda }_m=\frac{m\pi }{a}$ ， ${\lambda }_n=\frac{n\pi }{b}$ 。

$\begin{array}{l}{u}_0\left(x,y,t\right)={\displaystyle \underset{m=1}{\overset{\infty }{\sum }}{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}{U}_{mn}}}{\text{e}}^{i{\omega }_{n}t}\cos {\lambda }_{m}x\sin {\lambda }_{n}y\\ v_0\left(x,y,t\right)={\displaystyle \underset{m=1}{\overset{\infty }{\sum }}{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}{V}_{mn}}}{\text{e}}^{i{\omega }_{n}t}\sin {\lambda }_{m}x\cos {\lambda }_{n}y\\ w_b\left(x,y,t\right)={\displaystyle \underset{m=1}{\overset{\infty }{\sum }}{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}{W}_{bmn}}}{\text{e}}^{i{\omega }_{n}t}\sin {\lambda }_{m}x\sin {\lambda }_{n}y\\ w_s\left(x,y,t\right)={\displaystyle \underset{m=1}{\overset{\infty }{\sum }}{\displaystyle \underset{n=1}{\overset{\infty }{\sum }}{W}_{smn}}}{\text{e}}^{i{\omega }_{n}t}\sin {\lambda }_{m}x\sin {\lambda }_{n}y\end{array}$ (20)

将式(20)代入式(19)得到特征方程：

$\left\{\left[\begin{array}{cccc}{S}_{11}& S_{12}& S_{13}& S_{14}\\ S_{21}& S_{22}& S_{23}& S_{24}\\ S_{31}& S_{32}& S_{33}& S_{34}\\ S_{41}& S_{42}& S_{42}& S_{44}\end{array}\right]-{\omega }_n^2\left[\begin{array}{cccc}{M}_{11}& M_{12}& M_{13}& M_{14}\\ M_{21}& M_{22}& M_{23}& M_{24}\\ M_{31}& M_{32}& M_{33}& M_{34}\\ M_{41}& M_{42}& M_{42}& M_{44}\end{array}\right]\right\}\left\{\begin{array}{c}{U}_{mn}\\ V_{mn}\\ W_{bmn}\\ W_{smn}\end{array}\right\}=0$ (21)

5. 结果与讨论

本节将给出弹性地基在简支约束下无孔隙和有孔隙的FG板自由振动的数值结果，为了验证公式，将所得结果与已有三维精确解进行了对照，结果以表格的形式列出，平均误差定义如下

$误差\text{diff}=\left|\frac{本文模型结果}{3\text{D}精确结果}-1\right|\times 100\%$

材料特性 $E_c=380\text{GPa}$ ， ${\rho }_c=3800\text{kg}/{\text{m}}^{\text{3}}$ (c表示陶瓷相Al₂O₃)， $E_m=70\text{GPa}$ ， ${\rho }_m=2702\text{kg}/{\text{m}}^{\text{3}}$ (m表示金属相Al)，泊松比固定为( $v_m=v_c=0.3$ )，为方便起见使用无量纲形式如下

$\begin{array}{l}\hat{\omega }=\omega h\sqrt{\frac{\rho }{G}},\tilde{\omega }=\omega h\sqrt{\frac{{\rho }_m}{E_m}},\bar{\omega }=\omega \frac{a^2}{h}\sqrt{\frac{{\rho }_m}{E_m}},{\bar{K}}_w=\frac{K_w{a}^4}{{\eta }_{11}},{\bar{K}}_l=\frac{K_l{a}^4}{{\eta }_{11}},\\ {\bar{K}}_u=\frac{K_u{a}^4}{{\eta }_{11}},{\bar{K}}_s=\frac{K_s{a}^2}{{\eta }_{11}},{\bar{G}}_p=\frac{G_p{a}^2}{{\eta }_{11}},{\eta }_{11}=\frac{E_c{h}^3}{12\left(1-v_c^2\right)}\end{array}$

5.1. FG板

表1给出的两边简支FG板考虑不同纵横比(b/a)、厚度比(h/a)以及不同幂律指数(P)的无量纲基频，并将所得结果与Jin等人 [24] 提出的三维精确解和Mantari [25] 提出的改进理论以及Fatima Zohra Zaoui [26] 等人的准三维解进行了比较。结果表明本文所有结果都有很好的一致性。对于非常厚的矩形FG板，本文结果和准3D结果 [26] 存在一些局限性。原因是对于h = a/2的情况，结构形状是块而不再是板，此时剪切变形和厚度拉伸效应所起的作用非常重要。由于x和y方向采用相同的形函数来描述剪切应变沿板厚的分布，因此该模型更适用于方板分析(h = a/2，b = a)，而不适用于矩形板(h = a/2，b = 2a)。因此对于厚矩形板，可以采用三维弹性模型。

Table 1. Comparison of non-dimensional fundamental frequencies ω ˜ of FG plates

表1. FG板无量纲基频比较 $\tilde{\omega }$

5.2. 嵌入Winkler-Pasternak地基的FG板

不同幂律指数(P)下Winkler和Pasternak地基的弹性参数对FG板的无量纲基频的影响如表2所示。考虑了四种厚度比(h/a)，即0.05、0.1、0.15和0.2。在方板的情况下，考虑Winkler-Pastarek地基的FG板无量纲基频在所有厚度比范围内与准三维解的结果一致。从表中还可以看出无量纲基频随弹性刚度参数和厚度比的增大而增大，随幂律指数(P)的增加减小，这是由于弹性地基的刚度效应会使FG板的刚度增加，而随着幂律指数的增加，FG板变软。此外，幂律指数(厚度比)对嵌入Winkler地基的FG板的影响可以忽略不计(非常重要)，而对Pasternak地基的FG板的自由振动有很大影响。对于相同的幂律指数，

Table 2. Non-dimensional fundamental frequency ω ˜ of FG plates resting on Winkler-Pasternak foundations

表2. FG方板在Winkler-Pasternak地基上的无量纲基频 $\tilde{\omega }$

频率随弹簧参数K_w而缓慢增加，随剪切层参数G_p而迅速增加。当G_p值较大时，K_w对频率的影响可以忽略不计，原因是相较于K_w，G_p前的系数 ${\alpha }^2+{\beta }^2$ 过大。此外，G_p的变化改变了频率随幂律指数的变化趋势。在G_p = 0的情况下，频率随着梯度指数的增加而减小。但当G_p = 100时，频率随幂律指数适度上升。原因是G_p前 ${\alpha }^2+{\beta }^2$ 系数较大导致特征值结果不准确。由此可见，Pasternak/Kerr模型在预测剪切层刚度较大的FG板自由振动响应时存在缺陷。表3通过与3D和准3D结果的对比，验证了四变量理论对嵌入弹性地基中FG板和孔隙依赖FG板的振动性能的影响。描述孔隙效应有四种模式，即无孔隙(perfect)、孔隙均匀分布(imperfect-even)、孔隙非均匀分布(imperfect-uneven)和孔隙对数非均匀分布(imperfect-loga rithmic)，厚度比(h/a)选择0.05、0.1、0.15、0.2。在不考虑Winkler-Pasternak弹性地基的情况下，计算了有和无孔隙FG板的无量纲频率。从表中可以看出均匀分布会导致无量纲基频降低，固有频率随孔隙率增加而增加，而均匀分布的固有频率随孔隙率增加而减少。

Table 3. Variations of frequency parameters ω ¯ of porosity versus the Winkler-Pasternak foundation stiffness ( P = 1 )

表3. 孔隙率与Winkler-Pasternak地基刚度的变化对FG方板的频率 $\bar{\omega }$ 的影响( $P=1$ )

对于非均匀分布，对数函数的引入会导致无量纲频率降低。剪切参数对无量纲频率的影响显著，但所有孔隙分布模式下无量纲频率变化趋势保持恒定。

5.3. Kerr地基上的FGM板

表4分析了嵌入Kerr地基的FG板在不同弹性参数、厚度比(h/a)和幂律指数(P)下的固有频率变化。结果与Shahsavari的准三维解一致。与表2的结果相比，当 $K_s$ 和 $K_l$ 不变时，位于Kerr地基上的FG板的基频减小，这是因为考虑 $K_u=\infty$ 时，Kerr地基可以退化为到Pasternak地基，因此的Kerr地基相比Pasternak地基会使FG板的刚度减小，导致频率响应减小。但随着弹簧上刚度 $K_u$ 值的增大，固有频率的减小速率变缓。图2为FG板无量纲频率与厚度比、幂律指数和孔隙率的关系，根据基频斜率的变化可以观察到 $K_s$ 的变化对基频的影响大于 $K_u$ ，增加 $K_u$ ( $K_s$ , h/a)和幂律指数对固有频率的影响较小(较大，较大)，而增加 $K_u$ ( $K_s$ , P)和h/a对自然频率的影响较小(较大，较小)。

Table 4. Non-dimensional fundamental frequency ω ˜ of square FG plates resting on Kerr foundations ( K ¯ l = 100 )

表4. FG方板在Kerr地基上的无量纲基频 $\tilde{\omega }$ ( ${\bar{K}}_l=100$ )

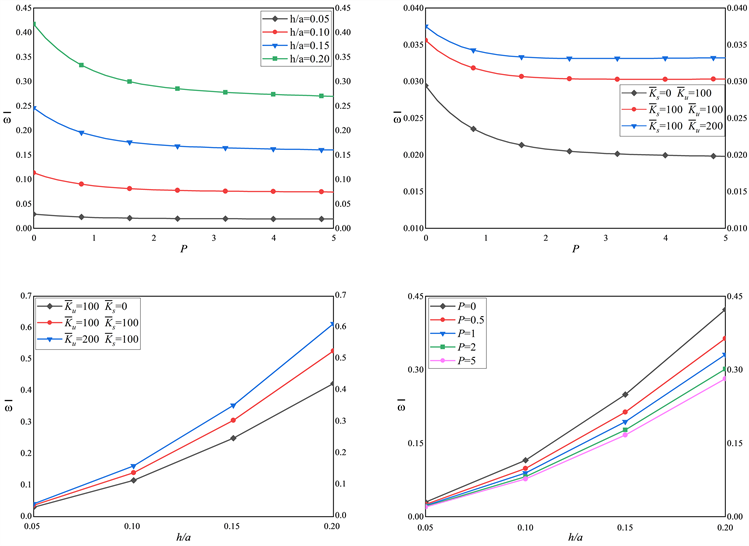
Figure 2. Effect of parameters ( $K_u,K_s,h/a,P$ ) on non-dimensional fundamental frequency $\tilde{\omega }$ of FG plates resting on Kerr foundation ( ${\bar{K}}_l=100$ )

图2. 参数( $K_u,K_s,h/a,P$ )对Kerr地基上FG板无量纲频率 $\tilde{\omega }$ 的影响( ${\bar{K}}_l=100$ )

表5研究了孔隙率的不同分布模式对嵌入Kerr地基矩形FG板无量纲频率的影响。对数函数的引入对高孔隙率的频率有重要影响，而对低孔隙率频率影响较小。随着弹性刚度参数( ${\bar{K}}_u$ , ${\bar{K}}_s$ )值的增加，弹性基础的整体刚度增加。为了明确孔隙率对FG板在软地基和硬地基的振动特性的影响，图3为FG板无量纲频率在厚度比恒定( $h/a=0.1$ )时与幂律指数和弹性刚度参数的关系。从该图可以看出，FG板的幂律指数(P)对具有孔隙均匀分布和孔隙不均匀分布的FG板振动有显著影响。在软地基中的FG板，孔隙不均匀分布比孔隙均匀分布，在高幂律指数时无量纲频率更大，而在硬地基中的FG板在所有幂律指数范围内，孔隙均匀分布的FG板基频最大。

Table 5. Variations of frequency parameters ω ¯ of porosity versus the Kerr foundation stiffness ( P = 1 , K ¯ l = 100 )

表5. 孔隙率与Kerr地基弹性刚度参数的变化对FG方板的频率 $\bar{\omega }$ 的影响( $P=1$ , ${\bar{K}}_l=100$ )

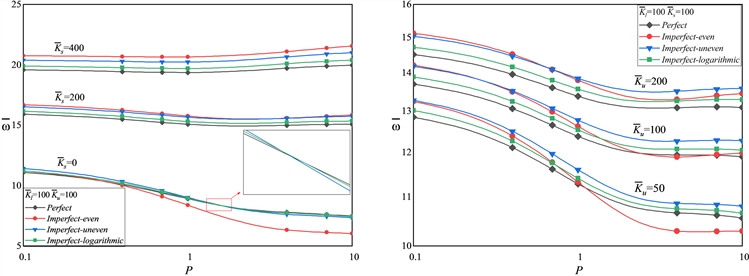
Figure 3. Variation of non-dimensional frequency $\bar{\omega }$ of FG plates resting on Kerr foundation versus power-law index for different spring parameters and shear layer parameters ( $\xi =0.2$ , $P=1$ )

图3. 幂律指数和弹性刚度参数对嵌入Kerr地基的FG板无量纲频率 $\bar{\omega }$ 的影响( $\xi =0.2$ , $P=1$ )

6. 结论

本文对嵌入弹性地基的孔隙依赖FG板进行了振动分析。孔隙模式分为均匀分布、非均匀分布和对数非均匀分布，材料内部的孔隙对FG板有一定的刚度软化作用，孔隙率的体积分数对FG板的固有频率起主导作用。均匀分布FG板的基频均随幂律指数和孔隙率的增大而减小，而非均匀分布FG板的基频随幂律指数和孔隙率的减小和增加。因此，非均匀分布的FG板弹性模量大于均匀分布的FG板，在相同孔隙率参数、长细比和幂律指数下，非均匀分布的FG板频率值较高。在均匀孔隙率分布和不均匀孔隙率分布中，无量纲频率分别随孔隙率参数的增大而减小和增大。

参考文献