L_(r,c)非负矩阵分解用于图像聚类

L_(r,c) Nonnegative Matrix Factorization for Image Clustering

摘要: 在非负矩阵分解用于聚类的过程中，将每一张大小为r × c灰度图像按列重排成一个样本向量会改变图像数据原有的空间结构，而目标函数直接度量样本向量与重构向量之间的误差会进一步忽略原始图像与重构后图像列之间的相似度。因此，为降低图像数据空间结构的改变对聚类效果的不利影响，本文提出了一种新的损失函数来逐列度量原始图像数据与重构后的图像数据间的误差，并推导了相应的数值算法。数值实验结果表明本文提出的算法有更好的聚类表现，图像表示能力更强。

Abstract: In the process of non-negative matrix factorization for clustering, rearranging each grayscale image with size r × c into a sample vector will change the original spatial structure of the image data, and the objective function directly measures the error between the sample vector and the reconstruc-tion vector to further ignore the similarity between the original image and the reconstructed image column. Therefore, in order to reduce the adverse effect of the change of spatial structure of image data on the clustering effect, a new loss function is proposed to measure the error between the original image data and the reconstructed image data column-by-column, and the corresponding numerical algorithm is derived. Numerical experimental results show that the proposed algorithm has better clustering performance and stronger image representation ability.

1. 引言

Lee和Seung于1999年提出非负矩阵分解(NMF) [1] 以来，NMF已广泛应用于数据挖掘和机器学习等领域。作为一种数据降维方法，非负矩阵分解将数据矩阵近似表示成两个非负因子矩阵的乘积，非负性约束使得该方法具有整体由部分表示的可解释性 [2] 。这使得NMF在文本挖掘 [3] 、模式识别 [4] 、DNA基因表达分析 [5] 等诸多方面得以广泛应用。根据具体问题的不同，人们提出了具有不同目标函数的NMF的衍变算法并将之应用于协同过滤、分类、约束聚类 [6] 等数据分析任务。C Ding等理论上分析了NMF与K-means聚类的潜在联系 [7] 。

在图像聚类任务中，NMF以矩阵的Frobenius范数作为目标函数度量样本数据矩阵与重构后的矩阵元素间的整体误差，由于该目标函数对噪声和异常值不稳定 [8] ，且忽视了原始图像数据与重构后的图像列与列之间的近似关系，是重构后的数据矩阵对原始图像数据的“粗糙”近似。C Ding [9] 等使用矩阵的 $L_{2,1}$ 范数作为目标函数，提出具有鲁棒性(robustness)的 $L_{2,1}$ NMF，相较于NMF而言， $L_{2,1}$ NMF的目标函数度量是原始图像数据重排后的样本向量与重构后的矩阵列向量之间的误差，虽然相较于NMF而言， $L_{2,1}$ NMF能够获得更为精细的图像表示，但仍然没有考虑到原始图像数据和重构后图像的列之间的近似关系。

因此，为使目标函数能够度量原始图像数据和重构后图像列之间的近似关系，从而减少原始图像数据空间结构的改变产生的影响，本文定义了向量的 $L_{\left(r,c\right)}$ 函数并提出相应的 $L_{\left(r,c\right)}$ NMF算法，该算法具有与 $L_{2,1}$ NMF相当的鲁棒性的同时，兼顾了原始图像数据的空间结构，实验结果上看 $L_{\left(r,c\right)}$ NMF算法也具有更好的图像表示能力和图像聚类表现。

后续内容安排如下：第二小节介绍了相关工作；第三小节定义 $L_{\left(r,c\right)}$ 函数，并定义 $L_{\left(r,c\right)}$ NMF算法的目标函数，从不等式推导和数值实验两方面说明 $L_{\left(r,c\right)}$ NMF算法的有效性；第四节推导给出算法的更新公式；第五小节引入辅助函数分析算法的收敛性；第六小节展示了 $L_{2,1}$ NMF算法和三种对比算法在三个数据集上的实验结果。

2. 相关工作

NMF是为了得到数据的部分表示 [1] 。给定一个非负矩阵 $X\in {ℝ}^{m\times n}$ ，NMF要将X近似表示成两个非负因子矩阵 $U\in {ℝ}^{m\times k}$ 和 $V\in {ℝ}^{k\times n}$ 的乘积，即：

$X\approx UV$ (1)

为了求解U和V，对如下目标函数最小化：

$\begin{array}{l}{\mathcal{Q}}_{NMF}={\Vert X-UV\Vert }_F^2=\underset{i,j}{{\displaystyle \sum }}{\left(X-UV\right)}_{ij}^2\\ \text{s}\text{.t}.U\ge 0,V\ge 0\end{array}$ (2)

其中 ${\Vert A\Vert }_F^2={\displaystyle {\sum }_{i,j}{A}_{ij}^2}$ 表示矩阵A的Frobenius范数。

Lee和Seung [2] 给出了相应的更新公式：

$U_{ij}=U_{ij}\frac{{\left(X{V}^{\text{T}}\right)}_{ij}}{{\left(UV{V}^{\text{T}}\right)}_{ij}}$ (3)

$V_{ij}=V_{ij}\frac{{\left(U^{\text{T}}X\right)}_{ij}}{{\left(U^{\text{T}}UV\right)}_{ij}}$ (4)

然而，NMF以Frobenius范数为目标函数会导致该算法对噪声和异常值敏感 [8] ，为解决这一问题，D Kong和C Ding等提出了具有鲁棒性的 $L_{2,1}$ NMF，该算法以矩阵的 $L_{2,1}$ 范数为目标函数，定义如下：

$\begin{array}{l}{\mathcal{Q}}_{L21NMF}={\Vert X-UV\Vert }_{2,1}=\underset{j}{{\displaystyle \sum }}\Vert x_j-U{v}_j\Vert \\ \text{s}\text{.t}.U\ge 0,V\ge 0\end{array}$ (5)

其中 $\Vert a\Vert =\sqrt{{\displaystyle {\sum }_i{a}_i^2}}$ 表示向量的2范数。

文 [11] 中给出了相应的更新公式：

$U_{ij}=U_{ij}\frac{{\left(XD{V}^{\text{T}}\right)}_{ij}}{{\left(UVD{V}^{\text{T}}\right)}_{ij}}$ (6)

$V_{ij}=V_{ij}\frac{{\left(U^{\text{T}}XD\right)}_{ij}}{{\left(U^{\text{T}}UVD\right)}_{ij}}$ (7)

其中D是对角矩阵，对角元素定义如下：

$D_{jj}=1/\Vert x_j-U{v}_j\Vert$ (8)

在图像聚类任务中，图像数据矩阵 $X\in {ℝ}^{rc\times n}$ 的每一列 $x_j\in {ℝ}^{rc\times 1}$ 都是由一张分辨率为 $r\times c$ 的灰度图像按列重排后的样本向量，即 $x_j$ 的每r个元素就是灰度图像中的一列。对比式(2)和式(5)可以看出，NMF度量X与UV所有元素间的误差，而 $L_{2,1}$ NMF度量的是样本向量 $x_j$ 与重构后的数据矩阵列向量 $U{v}_j$ 间的误差。不难验证下式成立：

$\sqrt{{\displaystyle \underset{i,j}{\sum }{\left(X-UV\right)}_{ij}^2}}\le {\displaystyle \underset{j}{\sum }\sqrt{{\displaystyle \underset{i}{\sum }{\left(X-UV\right)}_{ij}^2}}}$ (9)

上式表明，样本数据矩阵与重构后数据矩阵列向量之间的误差达到设定的误差限时，矩阵元素间的整体误差也能达到误差限，反之则不然。这使得 $L_{2,1}$ NMF能够度量样本数据矩阵与重构后数据矩阵列向量间的近似关系，从实验结果上看， $L_{2,1}$ NMF表示出的图像较之NMF要更加精细。

然而， $L_{2,1}$ NMF度量的仍然忽略了原始图像数据与重构后的图像列之间的近似关系，这使得样本向量与重构后的样本向量间误差较小时并不能保证原始图像数据的列向量间的误差也足够小。

因此，本文考虑了新的目标函数来度量原始图像数据与重构后图像数据列之间的近似关系。

3. ${\Vert \cdot \Vert }_{\left(r,c\right)}$ 目标函数

3.1. ${\Vert \cdot \Vert }_{\left(r,c\right)}$ 函数

给定 $x\in {ℝ}^{rc\times 1}$ ，本文定义x的一个实值函数如下：

定义1

${\Vert x\Vert }_{\left(r,c\right)}:=\underset{p=1}{\overset{c}{{\displaystyle \sum }}}\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{x}_i^2},r,c\in {�}^{+}$ (10)

易验证， ${\Vert \cdot \Vert }_{\left(r,c\right)}$ 满足范数的三条性质：

(1) 正定性 (2) 齐次性 (3) 三角不等式

对 $\forall x,y\in {ℝ}^{rc\times 1},a,b\in ℝ$ ，我们有：

$\begin{array}{c}{\Vert ax\Vert }_{\left(r,c\right)}+{\Vert by\Vert }_{\left(r,c\right)}=\underset{p=1}{\overset{c}{{\displaystyle \sum }}}\sqrt{{\left(\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{\left(a{x}_i\right)}^2}+\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{\left(b{y}_i\right)}^2}\right)}^2}\\ \ge \underset{p=1}{\overset{c}{{\displaystyle \sum }}}\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{\left(a{x}_i\right)}^2+{\left(b{y}_i\right)}^2+2a{x}_{i}b{y}_i}\\ =\underset{p=1}{\overset{c}{{\displaystyle \sum }}}\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{\left(a{x}_i+b{y}_i\right)}^2}\\ ={\Vert ax+by\Vert }_{\left(r,c\right)}\end{array}$ (11)

当且仅当 $x=y$ 时，不等式取等，显然当 $a,b\ge 0$ 且 $a+b=1$ ， $x\ne y$ 时式(11)严格成立，因此 ${\Vert x\Vert }_{\left(r,c\right)}$ 是关于变量x的严格凸函数。对于向量 $x\in {ℝ}^{n\times 1}$ ，若 $r=n,c=1$ ，该实值函数是x的 $l_2$ 范数；若 $r=1,c=n$ ，则该实值函数是x的 $l_1$ 范数。限于定义中r，c是给定的，所以 ${\Vert \cdot \Vert }_{\left(r,c\right)}$ 并不是严格意义上 ${ℝ}^{n\times 1}$ 中的向量范数。

3.2. ${\Vert \cdot \Vert }_{\left(r,c\right)}$ NMF目标函数

为了对原始图像数据逐列度量误差，本文提出的 $L_{\left(r,c\right)}$ NMF的目标函数定义如下：

$\begin{array}{l}{\mathcal{Q}}_{L\left(r,c\right)NMF}=\underset{j}{{\displaystyle \sum }}{\Vert x_j-U{v}_j\Vert }_{\left(r,c\right)}\\ \text{s}\text{.t}.U\ge 0,V\ge 0\end{array}$ (12)

对于 $X,UV\in {ℝ}^{rc\times n}$ ，将 $X,UV$ 的每一列对应一张 $r\times c$ 的图像，借由式(9)，不难验证下式成立：

$\sqrt{\underset{i}{{\displaystyle \sum }}{\left(X-UV\right)}_{ij}^2}\le \underset{p}{{\displaystyle \sum }}\sqrt{\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}{\left(X-UV\right)}_{ij}^2}$ (13)

由上式可知，对于 $L_{\left(r,c\right)}$ NMF而言，当原始图像数据与重构后的图像列之间的误差达到设定的误差限时， $L_{2,1}$ NMF的目标函数值也能达到，反之则不然。这使得本文给出的目标函数相较于NMF、 $L_{2,1}$ NMF更能在减少目标函数值的过程中兼顾原始图像数据和重构后图像列之间的近似关系。

4. $L_{\left(r,c\right)}$ NMF算法及鲁棒性说明

4.1. ${\Vert \cdot \Vert }_{\left(r,c\right)}$ NMF算法

本节给出 $L_{\left(r,c\right)}$ NMF算法的更新公式及推导过程。重述目标函数如下：

$\begin{array}{l}{\mathcal{Q}}_{L\left(r,c\right)NMF}=\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\underset{p=1}{\overset{c}{{\displaystyle \sum }}}{D}_{pj}=\underset{j,i}{{\displaystyle \sum }}\frac{{\left(X_{ij}-U{V}_{ij}\right)}^2}{D_{\lfloor \frac{i}{r+1}\rfloor +1,j}}\\ \text{s}\text{.t}.U_{ij}\ge 0,V_{ij}\ge 0\end{array}$ (14)

其中 $D_{pj}=\sqrt{{\displaystyle {\sum }_{t=r\left(p-1\right)+1}^{rp}{\left(X_{tj}-U{V}_{tj}\right)}^2}}$ ， $D\in {ℝ}^{c\times n}$ 。式(14)的拉格朗日函数如下：

${\mathcal{L}}_{L\left(r,c\right)NMF}=\underset{j,i}{{\displaystyle \sum }}\left[\frac{{\left(X_{ij}-U{V}_{ij}\right)}^2}{D_{\frac{i}{r+1}+1,j}}+U_{ij}{\Phi }_{ij}+U_{ij}{\Psi }_{ij}\right]$ (15)

$\frac{\partial {\mathcal{L}}_{L\left(r,c\right)NMF}}{\partial U_{ab}}={\left[\left(\Delta \odot \left(X-UV\right)\right)V^{\text{T}}\right]}_{ab}-{\Phi }_{ab}$ (16)

$\frac{\partial {\mathcal{L}}_{L\left(r,c\right)NMF}}{\partial V_{ab}}={\left[U^{\text{T}}\left(\left(X-UV\right)\odot \Delta \right)\right]}_{ab}-{\Psi }_{ab}$ (17)

其中 $\Delta \in {ℝ}^{rc\times n}$ ， ${\Delta }_{ij}=1/D_{\lfloor \frac{i}{r+1}\rfloor +1,j}$ ， $\odot$ 是哈达玛积(Hardamard product)，表示矩阵元素间的乘积。

由KKT条件 $\frac{\partial {\mathcal{L}}_{L\left(r,c\right)NMF}}{\partial U_{ab}}=0$ ， ${\Phi }_{ab}{U}_{ab}=0$ ； $\frac{\partial {\mathcal{L}}_{L\left(r,c\right)NMF}}{\partial V_{ab}}=0$ ， ${\Psi }_{ab}{V}_{ab}=0$ 即可得U和V的更新公式：

$U_{ij}=U_{ij}\frac{{\left(\left(\Delta \odot X\right)V^{\text{T}}\right)}_{ij}}{{\left(\left(\Delta \odot UV\right)V^{\text{T}}\right)}_{ij}}$ (18)

$V_{ij}=V_{ij}\frac{{\left(U^{\text{T}}\left(X\odot \Delta \right)\right)}_{ij}}{{\left(U^{\text{T}}\left(UV\odot \Delta \right)\right)}_{ij}}$ (19)

$L_{\left(r,c\right)}$ NMF算法见算法1。

4.2. ${\Vert \cdot \Vert }_{\left(r,c\right)}$ 函数的鲁棒性说明

我们使用二维数据点来说明 $L_{\left(r,c\right)}$ NMF的鲁棒性。示例的十个数据点中有三个是异常值，对每一个数据点 $x_i$ 我们使用 $U{v}_i$ 进行拟合，k值取1，如此我们把数据点投影到1维子空间中，实验中 $L_{\left(r,c\right)}$ NMF设定参数 $r=1$ ， $c=2$ 。给定的数据点以及分别使用NMF、 $L_{2,1}$ NMF和 $L_{\left(r,c\right)}$ NMF得到的拟合值见图1，从图中可以看出， $L_{\left(r,c\right)}$ NMF和 $L_{2,1}$ NMF得到的拟合值远离异常值的同时更加贴近原数据点，而NMF的拟合值则受到三个异常值的影响偏离了原数据点。对应数据点的残差 $\Vert x_i-U{v}_i\Vert$ 见图2，图中可以清晰地看出 $L_{\left(r,c\right)}$ NMF能够与异常值保持更大的残差从而减小异常值对拟合结果的影响，除开三个异常值处的残差外，相比于NMF而言， $L_{\left(r,c\right)}$ NMF和 $L_{2,1}$ NMF都有更小的残差。

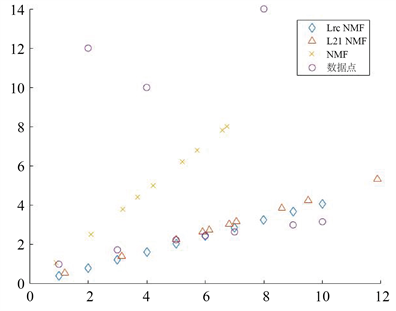
Figure 1. The results of fitting ten data points

图1. 拟合十个数据点的结果

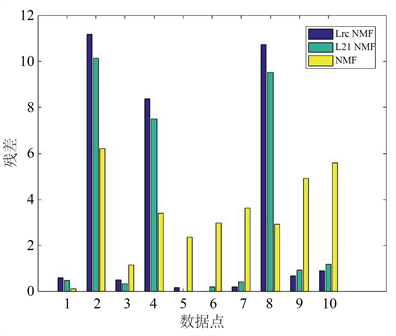
Figure 2. The residual histogram of fitting the data points

图2. 拟合数据点的残差直方图

为进一步说明 $L_{\left(r,c\right)}$ NMF的有效性。我们在数据集上运行 $L_{\left(r,c\right)}$ NMF、 $L_{2,1}$ NMF和NMF算法进行对比。本文展示Yale数据集上的对比结果。该数据集中，每一个 $x_i$ 都是由一张图像按列向量化所得，因此分解得到的基矩阵 $U=\left[u_1,u_2,\cdots ,u_k\right]$ 中的每一个向量 $u_i$ 也对应一张图像，将 $u_i$ 重排成原始大小的图像，展示见图3。

图像排成两行，每一行的上、中、下层分别是 $L_{\left(r,c\right)}$ NMF、 $L_{2,1}$ NMF和NMF算法收敛后得到的基矩阵U重排后的图像结果。从图像可见， $L_{\left(r,c\right)}$ NMF表示出的特征脸具有更加清晰的面部特征，例如对比明显的第一行的第1、2、5、6列和第二行的2、3、6、7、8列。总的来讲， $L_{\left(r,c\right)}$ NMF和 $L_{2,1}$ NMF都能降低数据中的噪声和异常值对算法的影响，而 $L_{\left(r,c\right)}$ NMF相较于 $L_{2,1}$ NMF进一步兼顾了原始图像数据的空间结构，因此能获得比 $L_{2,1}$ NMF更加清晰的图像表示结果。以上从理论和实验结果两方面说明了 $L_{\left(r,c\right)}$ NMF算法的有效性。

Figure 3. The base matrix obtained on the Yale dataset

图3. Yale数据集上得到的基矩阵

5. 收敛性分析

定理1 对于 $U\ge 0,V\ge 0$ ，目标函数 ${\mathcal{Q}}_{L\left(r,c\right)NMF}$ 在更新规则式(17)和式(18)下是非增的。

为证定理1，引入辅助函数的定义以及引理1。

定义2 如果下列条件满足：

$G\left(v_{ab},v_{ab}^t\right)\ge F\left(v_{ab}\right)$ (20)

$G\left(v_{ab}^t,v_{ab}^t\right)=F\left(v_{ab}^t\right)$ (21)

则称 $G\left(v_{ab},v_{ab}^t\right)$ 是 $F\left(v_{ab}\right)$ 的一个辅助函数。

引理1 若 $G\left(v_{ab},v_{ab}^t\right)$ 是 $F\left(v_{ab}\right)$ 的辅助函数，那么 $F\left(v_{ab}\right)$ 在下列更新规则下是非增的：

$v_{ab}^{t+1}=\arg \underset{v_{ab}}{\min }G\left(v_{ab},v_{ab}^t\right)$ (22)

证明：由定义2及引理1有

$F\left(v_{ab}^{t+1}\right)=G\left(v_{ab}^{t+1},v_{ab}^t\right)\le G\left(v_{ab}^t,v_{ab}^t\right)=F\left(v_{ab}^t\right)$

接下来给出辅助函数。记 $F\left(v_{ab}\right)$ 是目标函数 ${\mathcal{Q}}_{L\left(r,c\right)NMF}$ 关于 $v_{ab}$ 的部分， $F\left(v_{ab}\right)$ 对 $v_{ab}$ 的一阶导 $F^{\prime }\left(v_{ab}\right)$ 和二阶导 $F^{″}\left(v_{ab}\right)$ 分别如下：

$F^{\prime }\left(v_{ab}\right)={\left[U^{\text{T}}\left(\left(UV-X\right)\odot \Delta \right)\right]}_{ab}$ (23)

$F^{″}\left(v_{ab}\right)=\underset{p=1}{\overset{c}{{\displaystyle \sum }}}{\left(\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}\frac{U_{ia}^2}{D_{pb}}-\frac{S}{D_{pb}^3}\right)}_{ab}$ (24)

其中 $S={\left({\displaystyle {\sum }_{i=r\left(p-1\right)+1}^{rp}\left(U{V}_{ib}-X_{ib}\right)U_{ia}}\right)}^2$ 。

引理2 函数

$G\left(v_{ab},v_{ab}^t\right)=F\left(v_{ab}^t\right)+F^{\prime }\left(v_{ab}^t\right)\left(v_{ab}-v_{ab}^t\right)+\frac{1}{2}\frac{{\left(U^{\text{T}}\left(UV\odot \Delta \right)\right)}_{ab}}{v_{ab}^t}{\left(v_{ab}-v_{ab}^t\right)}^2$ (25)

是 $F\left(v_{ab}\right)$ 在 $v_{ab}^t$ 处的辅助函数。

证明：取 $F\left(v_{ab}\right)$ 在 $v_{ab}^t$ 处的泰勒展式

$F\left(v_{ab}\right)=F\left(v_{ab}^t\right)+F^{\prime }\left(v_{ab}^t\right)\left(v_{ab}-v_{ab}^t\right)+\frac{1}{2}{F}^{″}\left(v_{ab}^t\right){\left(v_{ab}-v_{ab}^t\right)}^2$ (26)

$\begin{array}{c}{F}^{″}\left(v_{ab}\right)=\underset{p=1}{\overset{c}{{\displaystyle \sum }}}\left(\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}\frac{U_{ia}^2}{D_{pb}}-\frac{S}{D_{pb}^3}\right)\le \underset{p=1}{\overset{c}{{\displaystyle \sum }}}\left(\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}\frac{U_{ia}^2}{D_{pb}}\right)\\ \le \underset{p=1}{\overset{c}{{\displaystyle \sum }}}\left(\underset{i=r\left(p-1\right)+1}{\overset{rp}{{\displaystyle \sum }}}\frac{U{V}_{ib}{U}_{ia}}{D_{pb}}\right)=\frac{{\left(U^{\text{T}}\left(UV\odot \Delta \right)\right)}_{ab}}{v_{ab}}\end{array}$ (27)

故 $G\left(v_{ab},v_{ab}^t\right)\ge F\left(v_{ab}\right)$ 成立，显然，当 $v_{ab}=v_{ab}^t$ ，有 $G\left(v_{ab}^t,v_{ab}^t\right)=F\left(v_{ab}^t\right)$ ，引理1得证。

易知 $G\left(v_{ab},v_{ab}^t\right)$ 是关于 $v_{ab}$ 的二次函数，可得：

$v_{ab}^{t+1}=\arg \underset{v_{ab}}{\min }G\left(v_{ab},v_{ab}^t\right)=v_{ab}^t-\frac{F^{\prime }\left(v_{ab}\right)}{\frac{{\left(U^{\text{T}}\left(UV\odot \Delta \right)\right)}_{ab}}{v_{ab}^t}}=v_{ab}^t\frac{{\left(U^{\text{T}}\left(X\odot \Delta \right)\right)}_{ab}}{{\left(U^{\text{T}}\left(UV\odot \Delta \right)\right)}_{ab}}$ (28)

该式恰是更新规则式(19)，故而定理1得证。篇幅所限，关于U的证明不再赘述。

6. 数值实验

本节使用本文提出的 $L_{\left(r,c\right)}$ NMF算法进行图像聚类实验，并与K-means、NMF算法 [2] 和 $L_{2,1}$ NMF算法 [9] 以及GNMF算法 [10] (正则项参数根据文献设定为10)进行图像聚类效果比较，实验使用的数据集是Yale、ORL。

6.1. 数据集介绍

Yale包含15个人，每个人不同表情、姿态和光照下的11张人脸图像，共165张图片，每张图片大小为32 × 32。

ORL包含40个人，每个人不同表情、姿态和光照下的10张人脸图像，共400张图片，每张图片大小为32 × 32。

6.2. 评估指标

本文以广泛使用的聚类精度(ACC)、归一化互信息(NMI)作为评估指标 [11] [12] 。

聚类精度(ACC)定义如下：

$\text{ACC}=\frac{{\displaystyle {\sum }_{i=1}^n\delta \left(s_i,map\left(r_i\right)\right)}}{n}$

其中 $s_i$ 是样本点的真实标签， $r_i$ 是算法得到的该样本点的聚类标签，n是数据样本总数， $\delta \left(x,y\right)$ 定义如下：

$\delta \left(x,y\right)=\{\begin{array}{l}1,x=y\\ 0,x\ne y\end{array}$

$map(.)$ 是置换映射函数(permutation mapping function)，Kuhn-Munkres算法可以得到最佳映射 [13] 。

记C为真实标签集合， $C^{\prime }$ 为算法获得的聚类标签，两者的互信息(mutual information)定义如下：

$MI\left(C,C^{\prime }\right)=\underset{c_i\in C,{c^{\prime }}_j\in C^{\prime }}{{\displaystyle \sum }}p\left(c_i,{c^{\prime }}_j\right){\log }_2\frac{p\left(c_i,{c^{\prime }}_j\right)}{p\left(c_i\right)p\left({c^{\prime }}_j\right)}$

其中 $p\left(c_i\right)$ 和 $p\left({c^{\prime }}_j\right)$ 分别是从数据集中任意选取一个样本，该样本属于 $c_i$ 和 ${c^{\prime }}_j$ 所在类的概率，而 $p\left(c_i,{c^{\prime }}_j\right)$ 则表示任意选取一个样本，该样本同属于 $c_i$ 和 ${c^{\prime }}_j$ 所在类的联合概率(joint probability)。

归一化互信息(NMI)定义如下：

$\overline{MI}=\frac{MI\left(C,C^{\prime }\right)}{\max \left(H\left(C\right),H\left(C^{\prime }\right)\right)}$

$H\left(C\right)$ 、 $H\left(C^{\prime }\right)$ 分别是C、 $C^{\prime }$ 的熵(entropies)。 $\overline{MI}\in \left[0,1\right]$ ，若两集合相同，则 $\overline{MI}=1$ ；两集合无关，则 $\overline{MI}=0$ 。

6.3. 参数设置

本文提出的 $L_{\left(r,c\right)}$ NMF需要根据原始图像数据的大小来确定 和 的值。在实验所用的Yale和ORL数据集中，每个样本向量表示一张32行、32列的原始图像，这两个数据集上 $r=32$ ， $c=32$ 。

本文的数值实验环境为：Matlab 2016a，11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz 2.30 GHz，16.00GB内存，Windows1164位操作系统。

具体步骤如下：

步骤一：从数据集中随机选取k类样本；

步骤二：使用算法1对选取的样本数据矩阵进行分解得到V；

步骤三：使用k-means算法对V进行聚类；

步骤四：计算ACC和NMI两个聚类指标。

重复上述步骤15次，记录ACC和NMI的平均值。

Table 1. Experimental results of three algorithms on the Yale dataset

表1. 三种算法在Yale数据集上的实验结果

Table 2. Experimental results of the three algorithms on the ORL dataset

表2. 三种算法在ORL数据集上的实验结果

7. 结论

本文定义了具有鲁棒性且兼顾原始数据图像空间结构的 $L_{\left(r,c\right)}$ 函数并给出相应的 $L_{\left(r,c\right)}$ NMF算法，拟合测试数据时目标函数具有较好的抗噪(robustness)表现，图像数据集上聚类实验结果可看出， $L_{\left(r,c\right)}$ NMF算法兼顾了原始图像数据结构，相对于K-means、NMF算法和 $L_{2,1}$ NMF算法以及GNMF算法而言在AC和NMI指标下具有更好的聚类性能，实验结果见表1、表2。以上均证实了本文算法的有效性。