堤坝渗漏感应磁梯度检测可行性研究

Dam Leakage Sensing Magnetic Gradient Detection Feasibility Study

摘要: 堤坝的渗漏检测对堤坝的安全运行有着重要的意义。由于磁梯度测量具有观测无需与地面接触、野外容易操作以及受地磁场影响较小等优点，该技术可以很好的应用于堤坝渗漏检测当中。为了研究磁梯度张量与渗漏通道之间的关系，本文从频率域Maxwell方程组出发推导控制方程，利用有限元实现了三维频率域磁场正演，并通过理论模型测试了算法的正确性。利用高阶紧致差分算法实现了磁梯度张量的高精度计算。接着文章分析了不同模型参数磁梯度张量和渗漏通道之间的关系，表明Byz和Bzz分量可以很好的反映渗漏通道的位置。通过对磁梯度的求解避免了理论计算磁场所带来的误差，并且提高了异常分辨率。通过本文的研究，可以为实际工作中的参数设计提供理论指导。

Abstract: The leakage detection of dam is of great significance for the safe operation. Because the magnetic gradient measurement has the advantages of no need to contact the ground, it is easy to operate, and it is less affected by the ground magnetic field when observing. This technology can be well applied in the leak detection. In order to study the relationship between the magnetic gradient and the leakage, this article derives the control equation from the frequency domain Maxwell equation, uses the finite element to achieve the 3D frequency domain magnetic field forward, and tests the correctness of the algorithm through the theoretical model. High-order compact difference scheme is used to achieve the high-precision calculation of magnetic gradient tensor. Then this article analyzes the relationship between the gradient tensor and the leakage channel of different model parameters. It shows that Byz and Bzz can reflect the position of the leakage channel. The solution to the magnetic gradient avoids the error caused by the theoretical calculation of the magnetic place, and improves abnormal resolution. Through the research of this article, the theoretical guidance can be provided for parameter design in actual work.

1. 引言

随着大型水利工程建设的基本完成，逐步进入后水电时代，处于工程运营期，堤坝的渗漏是影响其安全有效运营的重要问题 [1] [2] 。在长期复杂的自然环境条件下，土石堤坝状态不断发生变化，再加上施工质量和防渗处理等问题，导致现今大部分土石堤坝都存在一定的渗漏风险，渗漏问题不仅影响水电工程的经济效益，还会给堤坝运行带来安全隐患 [3] 。为及时对其健康状况诊断和评估，合理的堤坝渗漏探测具有重要的意义。

地球物理探测法是一种间接探测方法，根据堤坝与通道之间物性差异获得渗漏通道的分布。其具有准确、高效以及不伤害坝体等优点，在堤坝渗漏方面有着广泛的应用。目前常用的堤坝隐患物探方法，包括自然电场法 [4] 、电阻率法 [5] 、探地雷达 [6] 、瞬变电磁法 [7] 以及流场拟合法 [8] 等。但是由于我国堤坝类型众多、结构多样以及渗漏情况复杂，当前检测技术的探测精度和速度很难满足要求，所以寻求一种新的方法将其应用到土石堤坝渗漏检测上尤为重要。

磁梯度检测技术是在磁电阻率法的基础上，通过在堤坝上下游布置两个电极，并利用导线将放置在较远处发射机提供的电磁信号供入坝体之中。然后在堤坝上方和水中测量多个磁场矢量并计算磁梯度，进而获得土石堤坝渗漏通道分布的一种电磁探测方法。磁电法的正演方面，主要方法有解析解法 [9] 、有限差分法 [10] 以及有限单元法 [11] 等。Yang等 [12] 将CSEM有限元正演引入到磁电法正演之中，其直接将CSEM在近区所测得的磁场作为MMR正演磁场，并证明了CSEM方法正演磁场更符合实际。有限单元法是地球物理数值模拟的重要方法，其在20世纪90年代被引入到电磁勘探领域 [13] 。徐世浙 [14] 在1994年出版了中文著作《地球物理中的有限单元法》书中详细叙述有限元法在地球物理中的一般步骤和基本原理。Schwarzbach等 [15] 开发了基于二次场算法的自适应高阶有限元程序，并使用该程序进行了海洋CSEM正演，研究了海底地形对测量的影响。刘寄仁等 [16] 将基于有理Krylov子空间的单极点模型降阶算法引入CSEM有限元正演，实现了CSEM正演快速高精度求解。当前CSEM有限单元法数值模拟已经能够模拟1D、2D和3D模型并且其精度和效率也有了很大提升，使用有限单元法能够适应磁梯度求解对磁场精度的要求。磁梯度测量方面，主要方法有中心差分 [17] 、三次样条差分 [18] 和紧致差分算法 [19] 等。

在磁电法实际应用中，一般利用理论计算获得场源和背景所产生的磁场，然后对实际获得的总磁场进行归一化得到磁电异常，以消除供电导线和背景产生的磁场。但受到地形等因素影响，这种方法需要进一步改进。随着磁传感器精度的提高，磁梯度的测量精度有了很大进步。而且该技术具有施工简单和对异常分辨率高等优点，能很好的用于土石堤坝渗漏检测之中。

本文从磁梯度测量的角度出发，首先利用频率域Maxwell方程组获得控制方程，在考虑有限场源形态的情况下，使用六面体有限元方法实现三维频率域磁场高精度正演，并通过理论模型测试算法的正确性。再者，选择合适的梯度求导技术实现磁梯度的高精度计算，分析堤坝渗漏通道磁梯度的分布规律。通过本文的研究可以为实际磁梯度渗漏通道检测提供一定的理论依据和技术指导。

2. CSEM有限元方法

2.1. CSEM有限元方程

传统的磁电阻率法正演采用的是直流电法的正演思路 [20] [21] ，静电场麦克斯韦方程组入手，推导MMR控制方程，其与实际发送的低频信号不符。为符合实际，本文借助CESM的正演思路解决三维磁场正演问题，其基本方法是将CSEM在近区所测得的磁场直接作为MMR正演磁场 [22] 。设角频率 $\omega$ 、谐变因子 ${\text{e}}^{i\omega t}$ ，从频率域Maxwell方程组 [23] 出发，

$\nabla \times E=-i\omega B$ (1)

$\nabla \times B={\mu }_0\left(J_s+\sigma E\right)$ (2)

$\nabla \cdot E=0$ (3)

$\nabla \cdot B=0$ (4)

其中， $\nabla$ 表示哈密顿算子， $E$ 表示电场强度， $B$ 表示磁感应强度， $J_s$ 表示场源电流密度， $\sigma$ 表示电导率， ${\mu }_0$ 表示真空磁导率。对式(1)两端取旋度，将式(2)代入，可得电场E的双旋度方程：

$\nabla \times \nabla \times E+k^{2}E=-i\omega {\mu }_0{J}_s$ (5)

式中 $\omega$ 为圆频率，k为准静态极限下的波数，其中 $k^2=i\omega {\mu }_0\sigma$ 。应用伽辽金法便可得到关于电场的有限元方程 [24] ：

$R={\displaystyle \underset{c=1}{\overset{N_e}{\sum }}{\displaystyle {\iiint }_{{\Omega }_{•}}{N}_i^e}}\cdot \left(\nabla \times \nabla \times E+k^{2}E+i\omega \mu J_s\right)\text{d}{\Omega }_e$ (6)

其中 $N_e$ 为网格剖分的单元数目， $N_i^e$ 为单元棱边上的基函数。

2.2. 有限元分析

本文使用六面体单元，其基函数即有大小，又有方向，对于某一个单元，构造如下矢量基函数 [25]

$N_i^e=\frac{1}{8}\left(1+{\xi }_i\xi \right)\left(1+{\eta }_i\eta \right)\left(1+{\zeta }_i\zeta \right)$ (7)

其中 ${\xi }_i,{\eta }_i,{\varsigma }_i$ 为母单元中节点， $i=1,\cdots ,8$ 。

若已获得单元棱边中点的电场值 $E_{pi}^e\left(p=x,y,z;i=1,2,3,4\right)$ ，则根据矢量基函数可以求出该单元内任意位置的场值：

$E^e={\displaystyle \underset{i=1}{\overset{12}{\sum }}{N}_i^e}{E}_i^e$ (8)

研究区域进行网格剖分之后，接着对有限元方程进行离散，将整体区域的积分转化成单元积分的和。对式利用矢量恒等式及高斯定理可得：

$R={\displaystyle \underset{c=1}{\overset{N_e}{\sum }}{\displaystyle {\iiint }_{{\Omega }_e}\left(\nabla \times N_i^e\right)}}\cdot \left(\nabla \times E\right)+i\omega \mu N_i^e\cdot \sigma \cdot E+i\omega \mu N_i^e\cdot J_s)\text{d}{\Omega }_e+{\displaystyle {\int }_{se}\left[\left(\nabla \times E\right)\times N_i^e\right]}\cdot n_s\text{d}{S}_e$ (9)

当我们剖分区域选的足够远时，场值衰减为零，式(9)右端第二项为0。根据单元积分，可将任意单元的余量 $R^e$ 写为：

$R^e=\left(C_e+i\omega M_e\right)\cdot E_e+i\omega b_e$ (10)

式中， $\left(C_e+i\omega M_e\right)$ 为单元矩阵， $E_e$ 为电场矢量， $-i\omega b_e$ 为场源项。

2.3. 总体合成

将方程离散后得到的每个单元矩阵方程，通过合成，可得到总的矩阵方程 [26] [27] ，即：

$\left(C+i\omega M\right)\cdot E=-i\omega b$ (11)

式中， $\left(C+i\omega M\right)$ 为总体合成矩阵， $E$ 为电场矢量， $-i\omega b$ 为场源项。在求得电场矢量后，根据法拉第定律，即式(1)可得到磁场分量。

3. 高阶紧致差分算法

高阶紧致差分算法是具有低计算量且能保持高精度数值结果的差分方法 [28] 。本文采用非均匀网格三格点四阶紧致差分算法(third-point fourth-order compact difference scheme on the non-uniform grid, N-CD4)，以水平分量为例，其具体求导公式如下：

设 $x_i$ 为区间 $\left[a,b\right]$ 上的节点，步长 $h_i=x_{i+1}-x_i$ ， $i=0,1,\cdots ,N_x$ ，且将在第i个节点上的值表示为 $B_x^{i,j,k}$ ，其中 $i=0,1,\cdots ,N_x;j=0,1,\cdots ,N_y;k=0,1,\cdots ,N_z$ 。

令 $h_{bx}=x_i-x_{i-1}$ ， $h_{fx}=x_{i+1}-x_i$ ，内节点上磁梯度分量 $B_{xx}^{i,j,k}\left(i=1,2,\cdots ,N_x-1\right)$ 与磁场水平分量的四阶精度格式为 [19] ：

$\alpha B_{xx}^{i-1,j,k}+B_{xx}^{i,j,k}+\beta B_{xx}^{i+1,j,k}=\xi B_x^{i-1,j,k}+\psi B_x^{i,j,k}+\zeta B_x^{i+1,j,k},j=0,1,\cdots ,N_y;k=0,1,\cdots ,N_z.$ (12)

式中系数值为：

$\{\begin{array}{l}\alpha =\frac{h_{fx}^2}{{\left(h_{fx}+h_{bx}\right)}^2},\beta =\frac{h_{bx}^2}{{\left(h_{fx}+h_{bx}\right)}^2},\\ \xi =-\frac{2\left(h_{fx}^3+2h_{bx}{h}_{fx}^2\right)}{h_{bx}{\left(h_{bx}+h_{fx}\right)}^3}\psi =-\frac{2\left(h_{bx}-h_{fx}\right)}{h_{bx}{h}_{fx}},\zeta =\frac{2\left(h_{bx}^3+2h_{fx}{h}_{bx}^2\right)}{h_{fx}{\left(h_{bx}+h_{fx}\right)}^3}\end{array}$ (13)

对于左边界点和右边界点处，令 $h_{bx,1}=x_1-x_0,h_{fx,1}=x_2-x_1,h_{bx,N_x-1}=x_{N_x-1}-x_{N_x-2},h_{fx,N_x-1}=x_{N_x}-x_{N_x-1}$ ，

磁场水平分量的一阶导数紧致格式如下：

$\begin{array}{l}{B}_{xx}^{0,j,k}+\left(1+\frac{h_{bx,1}}{h_{fx,1}}\right)B_{xx}^{1,j,k}\\ =\frac{-3h_{bx,1}-2h_{fx,1}}{h_{bx,1}\left(h_{bx,1}+h_{fx,1}\right)}{B}_x^{0,j,k}+\left(\frac{2}{h_{bx,1}}-\frac{h_{bx,1}}{h_{fx,1}^2}+\frac{1}{h_{fx,1}}\right)B_x^{1,j,k}\\ +\frac{h_{bx,1}^2}{h_{fx,1}^2\left(h_{bx,1}+h_{fx,1}\right)}{B}_{xx}^{2,j,k},j=0,1,\cdots ,N_y;k=0,1,\cdots ,N_z.\end{array}$ (14)

$\begin{array}{l}\left(1+\frac{h_{fx,N_x-1}}{h_{bx,N_x-1}}\right)B_{xx}^{N_x-1,j,k}+B_{xx}^{N_x,j,k}\\ =-\frac{h_{fx,N_x-1}^2}{h_{bx,N_x-1}^2\left(h_{fx,N_x-1}+h_{bx,N_x-1}^{}\right)}{B}_{xx}^{N_x-2,j,k}-\left(\frac{2}{h_{fx,N_x-1}}-\frac{h_{fx,N_x-1}}{h_{bx,N_x-1}^2}+\frac{1}{h_{bx,N_x-1}}\right)B_x^{N_x-1,j,k}\\ +\frac{3h_{fx,N_x-1}+2h_{bx,N_x-1}}{h_{fx,N_x-1}\left(h_{bx,N_x-1}+h_{fx,N_x-1}\right)}{B}_x^{N_x,j,k},j=0,1,\cdots ,N_y;k=0,1,\cdots ,N_z.\end{array}$ (15)

通过求解上述等式，可以获得B_xx。同理，可以获得磁梯度其它分量B_xy、B_xz、B_yx、B_yy、B_yz、B_zx、B_zy和B_zz。

4. 正演模拟

4.1. 正演程序验证

为了验证六面体矢量有限元计算出的磁场精度同时比较两种梯度求解算法的稳定性和精度。我们设计了一个均匀半空间模型(图1)，并选取了一条测线，其具体参数如下：场源为偶极源，其电极位于轴上，长1 m。测线位于x = 15 m，y = 100~180 m，间隔1 m。发射频率128 Hz，电流强度1 A。

Figure 1. Sketch of model

图1. 模型示意图

图2分别是磁场三分量幅值和相对误差图，可以看出解析解和有限元计算出的磁场三个分量幅值基本一致，拟合效果较好，同时三个分量误差均小于1%。通过以上对比，证明三维有限元程序是正确的且精度满足要求。

在三维矢量有限元计算出的磁场基础上，本文采用三次样条差分(Cubic Splines Difference, CSD)和N-CD4两种算法分别计算了磁梯度(图3)，可以看出B_xx、B_xy、B_yx、B_yy、B_zx和B_zy分量两种算法计算出的幅值曲线完全重合，且曲线都较光滑。B_yz分量两种算法幅值曲线基本重合，其CSD算法曲线不太光滑。B_xz分量两者趋势一致，但CSD算法曲线有所跳动。B_zz分量N-CD4算法计算出的幅值曲线较光滑，而CSD算法曲线跳动比较严重，其原因是磁场的垂向分量在垂直方向上的变化较小，CSD算法的稳定性相较于N-CD4算法较弱所导致的。

综上，CSD和N-CD4两种算法都能计算磁梯度，而N-CD4的计算精度和稳定性优于CSD算法。故在后面模型计算时将采用N-CD4算法，进行三维渗漏通道磁梯度模拟。

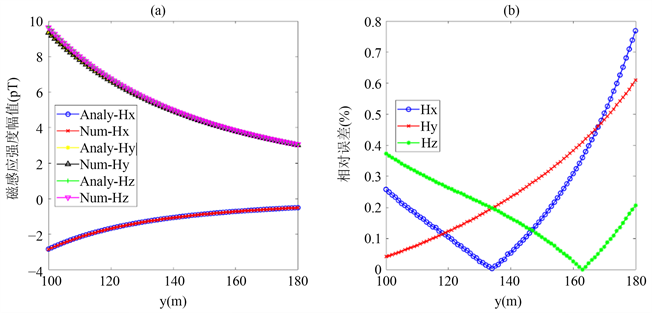
Figure 2. Comparison of numerical solution and analytical solution of inductive magnetic field vector. (a) Amplitude, (b) relative error

图2. 磁场矢量数值解与解析解对比图。(a) 幅值，(b) 相对误差

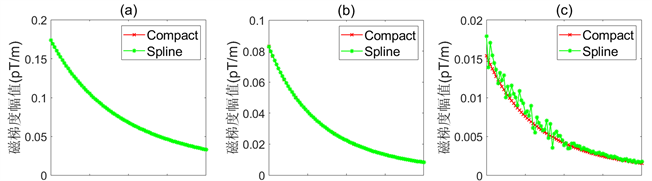
Figure 3. Comparison of magnetic gradient calculated by high-order compact difference and magnetic gradient calculated by cubic spline difference. (a) B_xx; (b) B_xy; (c) B_xz; (d) B_yx; (e) B_yy; (f) B_yz; (g) B_zx; (h) B_zy; (i) B_zz

图3. 高阶紧致差分与三次样条差分磁梯度计算结果对比图。(a) B_xx分量；(b) B_xy分量；(c) B_xz分量；(d) B_yx分量；(e) B_yy分量；(f) B_yz分量；(g) B_zx分量；(h) B_zy分量；(i) B_zz分量

4.2. 模型1

为了分析不同参数下异常体所引起的磁场矢量及磁梯度响应，本文设计了多个对比模型，以分析发射频率、异常体与背景电导率比值和异常体埋深对磁场矢量及磁梯度响应的影响。模型1的设计参数如下：

在一个电导率为0.001 S/m的均匀半空间内设置3个横截面积为0.25 m²，长21 m的长方体其电导率为0.1 S/m，埋深为10 m。设发射频率为128 Hz，电流为10 A，场源为U型源，其电极位于x轴上，x方向长300 m，总长1500 m。测区大小30 m × 60 m，测点间隔1 m (图4)。

由于导线供电电流较大且测区离场源较近，所以磁场矢量对异常体反映不太明显(图5)。而梯度是距离的变化量，对磁场矢量求导之后，其对磁场变化剧烈的地方更加敏感。

由于导线供电电流较大且测区离场源较近，所以磁场矢量对异常体反映不太明显(图5)。而梯度是距离的变化量，对磁场矢量求导之后，其对磁场变化剧烈的地方更加敏感。

由图6，B_yz分量可以很好的反映异常体的位置，B_yz幅值较大处即为异常体大致所在的位置，最大值为20 pT/m。其次，B_zz分量的大小值呈正负交替出现，在异常体上方为零点。B_zy分量在异常体的位置也有较好的反映，异常表现为极小值。同时，B_yy分量在异常体位置显示较小的异常，也可以看出异常体的大致位置。B_xy、B_zx和B_yx的幅值关于y轴呈中心对称出现，虽然异常体存在影响了曲线分布，但很难辨识。B_xx和B_xz无法显示异常体的位置。可以看出磁梯度在一定程度上可以反映异常体的位置，并且压制一次场的影响。

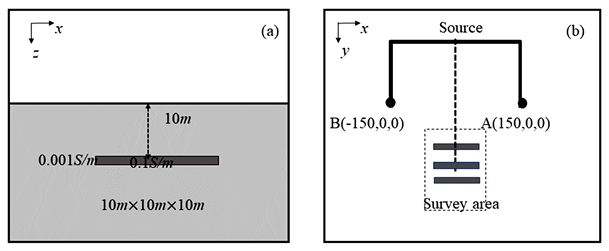
Figure 4. Sketch of 3D model. (a) Cross section; (b) plane view

图4. 3D模型示意图。(a) 剖面图；(b) 平面图

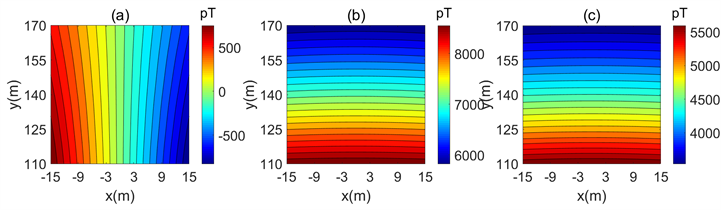
Figure 5. Distribution of inductive magnetic field vector. (a) B_x; (b) B_y; (c) B_z

图5. 感应磁场矢量分布图。(a) B_x分量；(b) B_y分量；(c) B_z分量

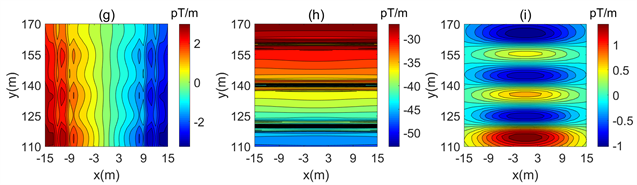
Figure 6. Distribution of inductive magnetic gradient tensor. (a) B_xx; (b) B_xy; (c) B_xz; (d) B_yx; (e) B_yy; (f) B_yz; (g) B_zx; (h) B_zy; (i) B_zz

图6. 感应磁梯度张量分布图。(a) B_xx分量；(b) B_xy分量；(c) B_xz分量；(d) B_yx分量；(e) B_yy分量；(f) B_yz分量；(g) B_zx分量；(h) B_zy分量；(i) B_zz分量

4.3. 模型2

在模型2中我们令三个异常体的电导率为0.05，而保持其他参数与模型1不变。研究电导率比值的变化对磁场矢量及梯度张量的影响。磁梯度分布如图7，图中可以看出B_yz和B_zz对异常体的反映依然存在，但相比于模型1其幅值减小。B_zy分量依旧可以看出极小值存在，幅值有所改变。B_yx和B_xy对异常的依旧很难辨识异常体的位置。B_zx对异常体反映减弱，B_xx和B_xz对异常体的反映依旧不理想。

4.4. 模型3

在模型3中我们改变三个异常体的埋深为15，而保持其他参数与模型1不变。研究异常体的埋深对磁场矢量及梯度张量的影响。

随着异常体的埋深增加，磁梯度分量出现了较大变化(图8)。其中，B_yz异常减小，对异常体的聚焦能力减弱，B_zz分量能看出其是沿y轴正负交替变化但不是很明显，场值减小值不到1 pT/m。B_xz在异常体上方的位置依然能看见其存在，B_yy分量已无法反映异常体的大体位置。说明磁梯度分量中随着埋深的增加梯度分量对异常的反映将会减弱。

4.5. 模型4

在模型4中我们令发射频率为64 Hz，而保持其他参数与模型1不变。研究场源发射频率对梯度张量的影响。图9所示，梯度张量的场值和分布基本与模型1一致，这是由于近区测量是几何测深，磁梯度分量受频率影响小，所以在野外可以选择增大频率以减小测量时间。

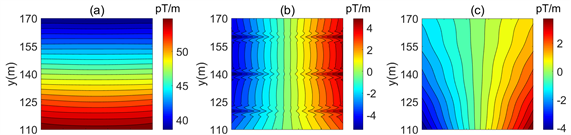
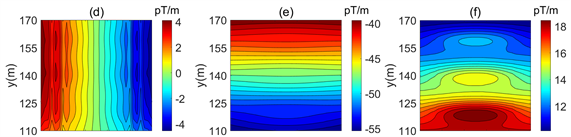
Figure 7. Distribution of inductive magnetic gradient tensor. (a) B_xx; (b) B_xy; (c) B_xz; (d) B_yx; (e) B_yy; (f) B_yz; (g) B_zx; (h) B_zy; (i) B_zz

图7. 感应磁梯度张量分布图。(a) B_xx分量；(b) B_xy分量；(c) B_xz分量；(d) B_yx分量；(e) B_yy分量；(f) B_yz分量；(g) B_zx分量；(h) B_zy分量；(i) B_zz分量

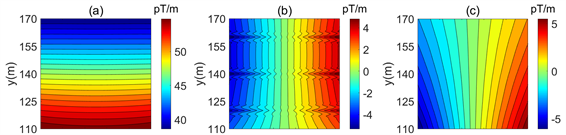
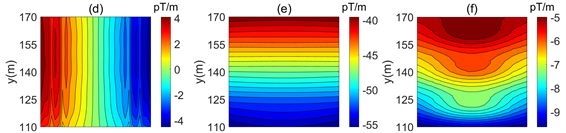
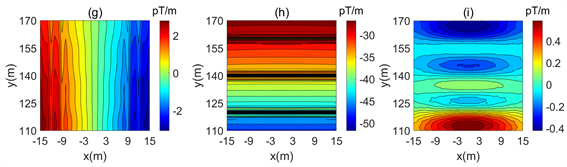
Figure 8. Distribution of inductive magnetic gradient tensor. (a) B_xx; (b) B_xy; (c) B_xz; (d) B_yx; (e) B_yy; (f) B_yz; (g) B_zx; (h) B_zy; (i) B_zz

图8. 感应磁梯度张量分布图。(a) B_xx分量；(b) B_xy分量；(c) B_xz分量；(d) B_yx分量；(e) B_yy分量；(f) B_yz分量；(g) B_zx分量；(h) B_zy分量；(i) B_zz分量

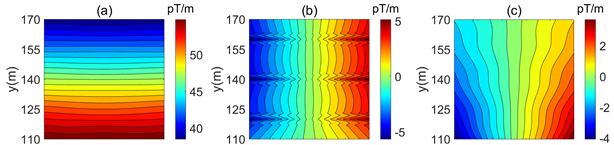
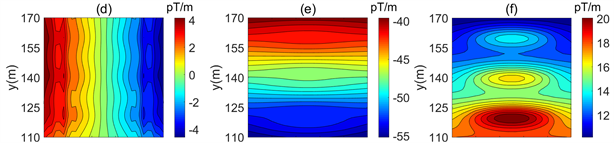
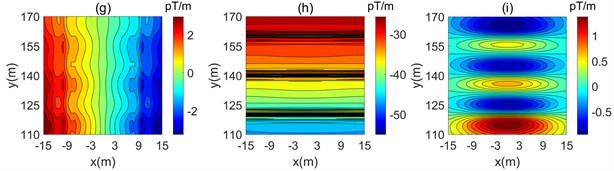
Figure 9. Distribution of inductive magnetic gradient tensor. (a) B_xx; (b) B_xy; (c) B_xz; (d) B_yx; (e) B_yy; (f) B_yz; (g) B_zx; (h) B_zy; (i) B_zz

图9. 感应磁梯度张量分布图。(a) B_xx分量；(b) B_xy分量；(c) B_xz分量；(d) B_yx分量；(e) B_yy分量；(f) B_yz分量；(g) B_zx分量；(h) B_zy分量；(i) B_zz分量

5. 结论

本文利用六面体矢量有限元和高阶紧致差分算法实现了磁梯度张量的高精度正演，并分析了不同参数下渗漏通道与磁梯度张量之间的关系。以更符合实际测量的CSEM方式正演MMR磁场，获得高精度磁场，采用紧致差分算法获得磁场梯度，避免了由理论计算出的磁场所带来的误差，并且提高了对渗漏通道异常的分辨率。首先由频率域Maxwell方程组出发获得控制方程，其次利用六面体矢量有限元方法实现了磁场的高精度计算，并与一维程序对比验证了其正演的精度。然后采用三次样条差分算法和高阶紧致差分算法实现了磁场梯度的正演，其中高阶紧致差分算法的精度和稳定性优于三次样条差分算法。接着建立了三个不同参数下的异常体模型，选用高阶紧致差分算法获得磁场梯度与不同模型参数之间的关系，表明B_yz和B_zz分量对异常的显示要优于其他分量，但B_zz分量数值较小。漏通道埋深越浅、电导率比值越大，磁梯度异常越明显。所以，在野外测量时建议最好测量B_yz分量来获得渗漏通道的分布，当渗漏通道较深时，也可以通过增大电流来获得更高的信噪比，获得更加明显的异常。

由于受到场源的影响，总场算法在正演磁场时需要对场源和测点加密以提高精度，在下一阶段可考虑基于二次场的高阶有限元进行正演，可以在保证精度的同时缩短正演时间。此外，本文方法能否成功应用的关键在于磁梯度张量的观测，研制合适的观测仪器和方法直接获取磁场梯度数据，是下一阶段的重点研究方向。