1. 引言
在材料科学和流体动力学中,通常会涉及到一些分片光滑的变系数二阶椭圆交面问题的数值求解。常用的数值方法包括有限元方法 [1] [2] [3] [4] [5] 和有限差分方法 [6] [7] [8] 。
文献 [9] 应用拟合有限元方法解决椭圆界面问题,并在有限元空间的一些近似假设下,得到了能量范数估计。文献 [3] 利用具有特殊拟合网格的标准有限元对拟合网格有限元方法进行估计。文献 [10] 提出了一种无限元素方法,可以看作是一种特定的网格细化方案,用于不适合弯曲界面的椭圆界面问题。文献 [11] 利用Nitsche方法,提出了椭圆界面问题的有限元法。然而,很少有关于用谱元法去处理圆域上一类分片光滑变系数二阶椭圆交面问题的报道,因此,本文针对圆域上一类变系数二阶椭圆交面问题提出一种有效的谱元法。首先,根据极坐标变换公式,极条件以及傅里叶基函数展开,原问题被分解为一系列关于径向变量的相互独立的一维二阶资源问题,并建立了弱形式和相应的离散格式。其次,我们根据变系数的正则性,构造了基于分片高阶多项式逼近的一种谱元方法,再通过利用勒让德多项式的正交性质,构造了一组适当的基函数,使得离散变分形式中的系数矩阵在变系数为分片多项式条件下是分块对角的稀疏矩阵。最后,我们呈现了一些数值例子,通过数值结果验证了我们提出的算法是收敛的和高精度的。
本文剩余部分安排如下:在第2节,我们推导圆域内变系数二阶椭圆问题的降维格式。在第3节,我们建立相应的弱形式及其离散格式。在第4节,我们详细描述算法的实现过程。在第5节中,我们呈现了几个数值例子。
2. 降维格式
作为一个模型,我们考虑下面的分片光滑的二阶椭圆交面问题:
(1)
(2)
其中
是一个径向函数,
,
是一个非光滑点。下面我们将推导方程(1)~(2)基于极坐标变换
的降维格式。令
则问题(1)~(2)可以化为下面的等价形式:
(3)
其中
。利用傅里叶基函数展开,有
(4)
将(4)代入(3),利用傅里叶基函数的正交性可得到(1)~(2)等价的一系列一维二阶椭圆交面问题:
(5)
(6)
(7)
3. 弱形式和离散格式
令
。定义一个通常的带权Sobolev空间:
其中,对应的内积以及范数分别如下:
进一步定义非一致带权Sobolev空间:
其中,对应的内积以及范数分别如下:
则(5)~(7)的一种弱形式为:找到
,使得
(8)
其中
是次数不超过N次的多项式,定义逼近空间:
则弱形式(8)相应的离散格式为:找到
,使得
(9)
4. 算法的有效实现
我们将在这一节详细描述算法的实现过程。首先,我们构造谱元逼近空间中的一组基函数。令
其中
,
表示i次勒让德多项式。我们分别定义如下的内部基函数:
其中
,
,
,
。则
的所有内部基函数为:
定义c处的交面基函数:
则逼近空间
可表示为:
1) 当
时,对离散格式(9)进行积分区间标准化:
其中
,
。将近似解
展开为:
则可得到离散格式(9)等价的矩阵形式为:
其中
其中
2) 当
时,对(9)进行积分区间标准化:
将近似解
展开为:
则可得到离散格式(9)等价的矩阵形式为:
其中
其中
5. 数值实验
为了验证该算法的有效性,我们将呈现一些数值实验。我们在MATLAB2017b平台上编程计算。令数值解与近似解之间的误差如下:
其中
(10)
例1我们取函数
,当取不同的M和N时,我们在表1中分别列出了数值解与近似解之间的误差结果。

Table 1. Error outcome between numerical solution and approximate solution for diverse N and M
表1. 当取不同的N和M时,数值解与近似解之间的误差结果
为了更加直观的表明算法的收敛性和高精度,在图1中依次给出了数值解与近似解的图像,在图2中依次给出了数值解与N = 30,M = 10和N = 40,M = 20时的近似解之间的误差图像。
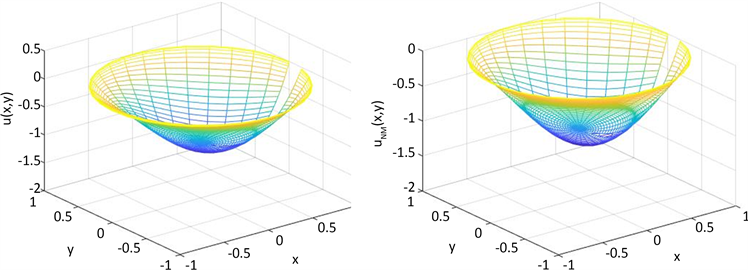
Figure 1. Graphics of numerical solution (left) and approximate solutions (right) for N = 30 and M = 12
图1. 数值解(左)与N = 30和M = 12时的近似解(右)的绘图
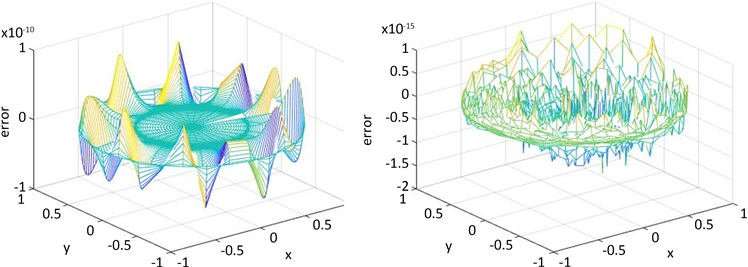
Figure 2. Error Graphics between the numerical solution and the approximate solution when N = 30, M = 10 (left) and N = 40, M = 20 (right)
图2. 数值解与N = 30,M = 10 (左)和N = 40,M = 20 (右)时的近似解之间的误差绘图
从表1的数据可以知道,当
时,近似解
达到了大约10−13的精度。最后,从图1和图2也能得到我们提出的算法是收敛的和高精度。