时滞递归神经网络的全局指数同步

Global Exponential Synchronization of Recurrent Neural Networks with Time Delays

摘要: 本文主要讨论了时滞递归神经网络中，驱动系统和响应系统的全局指数同步问题。本文首先考虑到时滞前后模板元素设计了驱动系统，为了直观地看出全局指数同步效果设计了误差相关的控制器；其次构造了Lyapunov泛函并用Filippov解证明了本文设计的控制器的可行性；最后通过实验发现本文设计的控制器可以使驱动和响应系统达到全局指数同步的效果。

Abstract: In this paper, we mainly discuss the global exponential synchronization of the driving system and the response system in the delayed recurrent neural networks. In this paper, the driving system is designed by considering the delay before and after the template elements. In order to see the global exponential synchronization effect intuitively, the error dependent controller is designed. Secondly, Lyapunov functional is constructed and Filippov solution is used to prove the feasibility of the controller designed in this paper. Finally, experiments show that the controller designed in this paper can make the drive and response system achieving the effect of global exponential syn-chronization.

1. 引言

神经网络 [1] 是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。其中递归神经网络 [2] 是具有树状阶层结构且网络节点按其连接顺序对输入信息进行递归的神经网络。

神经网络总是受到神经元放大器的开关速度有限和神经元之间的通讯时间传输延迟的影响，导致各神经元之间传输信息不同步，也就是驱动系统在启动时，相应的响应系统不能立即作出反应，中间会产生一定的时间延迟，所以Pecora [3] 等人首次提出了驱动和响应系统同步的概念，即两个或多个混沌或周期系统具有共同的动力学行为。这种同步应用于安全通信时，只有在驱动系统和响应系统实现完整的同步传输信号才可以成立，而且同步的作用会在模式识别 [4] 、图像处理 [5] 、医学诊断 [6] 等领域造成一定影响，于是研究神经网络之间的全局指数同步问题变得越来越重要。全局指数同步 [7] [8] [9] [10] [11] 的研究工作已经有了很多可以借鉴的资料，在不连续状态下神经网络的全局指数同步问题已经有文献进行了相关研究，比如在模糊神经网络 [12] 中研究了一类具有时变时滞和不连续激励的模糊神经网络在状态反馈控制和自适应控制下的全局指数同步问题，对激活函数做了相关假设，利用不连续状态反馈设计了控制器并且构造Lyapunov泛函，关于全局指数同步新的和有用的准则被提出，通过对响应系统设计新型控制器，从理论和数值上证明了响应系统可以与驱动系统实现全局指数同步，并且同步判据易于验证。在递归神经网络 [13] [14] [15] 中也是设计了不连续状态反馈控制器模型可以实现全局指数同步，非连续神经元激活的神经网络的稳定性问题引起了不同领域研究者的兴趣。因此，研究了具有不连续激活的神经网络的指数同步问题。同时考虑了状态反馈控制和自适应控制技术，所设计的控制器结构简单，可应用于具有间断和连续激活的神经网络。此外，文献中还考虑到了收敛速度是明确估计状态反馈控制的一个标准。这些文献的共同点都是构造李雅普诺夫泛函并结合Filippov解证明所提出的控制器可以使驱动和响应系统达到全局指数同步。

研究不同神经网络的全局指数同步问题已经成为了一个热点话题，但是有关递归神经网络的全局指数同步问题的研究较少。所以，在已有的研究基础上，本文选择更详细地分析时滞递归神经网络的驱动系统模型，证明本文设计的控制器可以有效地实现时滞递归神经网络的全局指数同步。

在上述讨论的基础上，本文主要研究了时滞递归神经网络的全局指数同步问题。本文在时滞微分方程的基础上，结合Filippov解 [16] 和初值问题 [17] 的定义，更细致地分析了时滞递归神经网络中时滞前后模板元素并建立了驱动系统模型。为了使驱动和响应系统达到全局指数同步的效果，本文对响应系统设计了一个控制器；为了证明提出的控制器的可行性，构造了Lyapunov泛函 [18] 并用链式法则进行了证明。利用初值问题的定义计算出了控制器的系数，通过实验发现，本文设计的控制器可以达到全局指数同步的效果。

本文的其余部分组织如下：第二节介绍了驱动系统和响应系统，此外，本文还给出了一些假设和定义以及一些有用的引理；第三节专门研究时滞递归神经网络的全局指数同步；第四节给出了数值实验，以说明主要结果的有效性；最后在第五节得出一些结论。

2. 模型构造及预备知识

本文讨论的不连续的时滞递归神经网络驱动系统如下：

${\stackrel{\dot{}}{x}}_i\left(t\right)=-o_i{x}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{f}_j}\left(x_j\left(t-\rho \left(t\right)\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i,i=1,2,\cdots ,n,$ (2.1)

$x_i\left(t\right)$ 表示第i个单元在时间t的状态； $o_i$ 表示被动衰减率到第i个单元的状态； $a_{ij}$ 表示反馈模板的元素； $c_{ij}$ 表示出现时滞的反馈模板的元素； $b_{ij}$ 表示前馈模板的元素； $d_{ij}$ 表示时滞后的前馈模板的元素； $v_i$ 和 $I_i$ 分别表示第i个神经元的输入和偏置； $f_i$ 表示激活函数； $\rho \left(t\right)\ge 0$ 表示对应于沿第i个单元的轴突的传输延迟。以矩阵形式表示如下：

$O=diag\left(o_1,o_2,\cdots ,o_n\right),A={\left(a_{ij}\right)}_{n\times n},B={\left(b_{ij}\right)}_{n\times n},C={\left(c_{ij}\right)}_{n\times n},D={\left(d_{ij}\right)}_{n\times n}.$

定义2.1 (欧几里得向量范数)给定列向量 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ ，其中上标“T”表示向量的转置， $\Vert x\Vert$ 是欧几里得向量范数

$\Vert \stackrel{\to }{X}\Vert =\sqrt{\underset{i}{\overset{n}{{\displaystyle \sum }}}{\left(x_i\right)}^2}=\sqrt{{\left(x_1\right)}^2+{\left(x_2\right)}^2+\cdots +{\left(x_n\right)}^2}={\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i^2}\right)}^{\frac{1}{2}}$

设 $I_n$ 和 $A={\left(a_{ij}\right)}_{n\times n}$ 分别为兼容维数的单位矩阵和方阵，设 $\Vert A\Vert$ 表示由 $\Vert A\Vert ={\lambda }_{\max }{\left(A^{\text{T}}A\right)}^{1/2}$ 定义的欧几里得范数。最后，用 $U\left[\Omega \right]$ 表示集合 $\Omega \subset R^n$ 的凸包的闭包。

对激活函数和时滞做如下假设。

假设1对于每个 $i=1,\cdots ,n$ 。 $f_i:R\to R$ 除了在一个独立点 $\left\{q_k^i\right\}$ 的可数集合上是连续的，其中分别存在有限的右、左极限 $f_i\left(q_k^{i_{+}}\right)$ 和 $f_i\left(q_k^{i_{-}}\right)$ 。此外， $f_i$ 在R的每个紧化区间中最多有有限个跳跃不连续点。

假设2对于每一个 $i=\left(1,\cdots ,n\right)$ ，存在非负常数 $h_i$ 和 $g_i$ 使得

$\left|{\vartheta }_i-{\mu }_i\right|\le h_i\left|x_i-y_i\right|+g_i$ (2.2)

并且由定义2.1可知 $\forall x_i,y_i\in R$ ， ${\vartheta }_i\in U\left[f_i\left(x_i\right)\right]$ ， ${\mu }_i\in U\left[f_i\left(y_i\right)\right]$ 。

假设3存在正常数 $\rho$ 和 ${\rho }^{*}$ ，使 $0<\rho \left(t\right)\le \rho$ ，和 $\stackrel{\dot{}}{\rho }\left(t\right)\le {\rho }^{*}<1$ 。显然，如果传输延迟 $\rho \left(t\right)$ 是连续的，则肯定能保证假设成立。

注意：

$U\left[f_i\left(y_i\right)\right]=\left[\min \left\{f_i\left(x_i^{i_{-}}\right),f_i\left(x_i^{i_{+}}\right)\right\},\max \left\{f_i\left(x_i^{i_{-}}\right),f_i\left(x_i^{i_{+}}\right)\right\}\right],i=1,\cdots ,n.$

这意味着当在 $f_i$ 在 $x_i$ 处不连续时， $U\left[f_i\left(y_i\right)\right]$ 是一个内部非空的区间，而当 $f_i$ 在 $x_i$ 处连续时， $U\left[f_i\left(y_i\right)\right]=\left\{f_i\left(x_i\right)\right\}$ 是一个单例。

由于激活函数满足假设1，(2.1)的右边是有关x的离散函数，因此有必要说明(式2.1)解的精确含义。我们采用了Filippov解给出合理定义。

定义2.2 (Filippov解)如果满足以下条件

1) $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ 在 $\left[-\rho ,T\right)$ 上连续，并且在 $\left[0,T\right)$ 上绝对连续；

2) 存在一个可测函数 $\vartheta ={\left({\vartheta }_1,{\vartheta }_2,\cdots ,{\vartheta }_n\right)}^{\text{T}}:\left[-\rho ,T\right)\to R^n$ ，使 ${\vartheta }_j\left(t\right)\in U\left[f_j\left(x_j\left(t\right)\right)\right]$ ， $t\in \left[-\rho ,T\right)$ 可知：

${\stackrel{\dot{}}{x}}_i\left(t\right)=-o_i{x}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{\vartheta }_j}\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\vartheta }_j}\left(t-\rho \left(t\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i,t\in \left[0,T\right),i=1,2,\cdots ,n,$ (2.3)

则称函数 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ 是驱动系统中在 $\left[-\rho ,T\right)\left(T\in \left(0,+\infty \right]\right)$ 上的一个解。

定义2.3 (初值问题)对于任意连续函数 $\phi ={\left({\phi }_1,{\phi }_2,\cdots ,{\phi }_n\right)}^{\text{T}}:\left[-\rho ,0\right]\to R^n$ 和任何可测量的选择 $\psi ={\left({\psi }_1,{\psi }_2,\cdots ,{\psi }_n\right)}^{\text{T}}:\left[-\rho ,0\right]\to R^n$ ，有 ${\psi }_j\left(s\right)\in U\left[f_j\left({\phi }_j\left(s\right)\right)\right]\left(j=1,\cdots ,n\right)$ 并且 $S\in \left[-\rho ,0\right]$ ，由初始条件与驱动系统相关的初值问题 $\left(\phi ,\psi \right)$ 可知：可以找到函数 $x\left(t\right),\gamma \left(t\right)$ ，使 $x\left(t\right)$ 是某个 $T>0$ 在 $\left[-\rho ,T\right)$ 上驱动系统上的解， $\vartheta \left(t\right)$ 是与 $x\left(t\right)$ 相关的输出解，并且有：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i\left(t\right)=-o_i{x}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{\vartheta }_j\left(t\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\vartheta }_j\left(t-\rho \left(t\right)\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i\\ {\vartheta }_j\left(t\right)\in U\left[f_j\left(x_j\left(t\right)\right)\right],t\in \left[0,T\right)\\ x_i\left(s\right)={\phi }_i\left(s\right),\forall s\in \left[-\rho ,0\right]\\ {\vartheta }_j\left(s\right)={\psi }_j\left(s\right),s\in \left[-\rho ,0\right]\end{array}$ (2.4)

驱动系统(式2.1)相关的响应系统如下：

${\stackrel{\dot{}}{y}}_i\left(t\right)=-o_i{y}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{f}_j}\left(y_j\left(t\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{f}_j}\left(y_j\left(t-\rho \left(t\right)\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i+u_i\left(t\right),i=1,2,\cdots ,n,$ (2.5)

上式中， $y_i\left(t\right)$ 对应响应系统第i个神经元的状态变量，其他参数的动态含义如驱动系统(2.1)，响应系统多加了一个 $u_i\left(t\right)$ 表示要设计的控制器，由Filippov解可知响应系统也可写成如下表达式：

${\stackrel{\dot{}}{y}}_i\left(t\right)=-o_i{y}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{\mu }_j\left(t\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\mu }_j\left(t-\rho \left(t\right)\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i+u_i\left(t\right),t\in \left[0,T\right),i=1,2,\cdots ,n,$ (2.6)

通过初值问题的定义可知：

$\{\begin{array}{l}{\stackrel{\dot{}}{y}}_i\left(t\right)=-o_i{y}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}{\mu }_j\left(t\right)}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{ij}{v}_j}+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\mu }_j}\left(t-\rho \left(t\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_{ij}{v}_j}+I_i+u_i(t)\\ {\mu }_j\left(t\right)\in U\left[f_j\left(y_j\left(t\right)\right)\right],t\in \left[0,T\right)\\ y_i\left(s\right)={\Phi }_i\left(s\right),\forall s\in \left[-\rho ,0\right]\\ {\mu }_j\left(s\right)={\chi }_j\left(s\right),s\in \left[-\rho ,0\right]\end{array}$ (2.7)

定义2.4令 $x\left(t\right)$ 是驱动系统， $y\left(t\right)$ 是响应系统，如果 $y\left(t\right)$ 中存在一个控制输入 $u_i\left(t\right)$ ，并且存在常数 $M\ge 1$ 和 $ϵ>0$ ，满足以下条件：

$\Vert x\left(t\right)-y\left(t\right)\Vert \le M\underset{-\rho \le s\le 0}{\sup }\Vert \phi -\Phi \Vert {\text{e}}^{-ϵt},t>0.$

可以说明驱动系统和响应系统能够达到全局指数同步。

这里的常数 $ϵ$ 指的是指数同步的程度。接下来，提出在建立全局指数同步准则中起重要作用的初步引理。

引理2.1 (Gronwall不等式)假设函数 $g\left(t\right)$ 和 $f\left(t\right)$ 在 $\left[t_0,t_1\right]$ 上连续， $t_0\le t\le t_1$ ，并且 $f\left(t\right)\ge 0$ ， $g\left(t\right)\ge 0$ ， $K\ge 0$ 为常数。如果

$f\left(t\right)\le K+{\displaystyle \underset{t_0}{\overset{t}{\int }}f\left(s\right)g\left(s\right)\text{d}s}$

$f\left(t\right)\le K\exp \left({\displaystyle \underset{t_0}{\overset{t}{\int }}g\left(s\right)\text{d}s}\right)$

引理2.2 (链式法则)若I，J是直线上的开区间，函数 $f\left(x\right)$ 在I上有定义 $a\left(\in I\right)$ 处可微，函数 $g\left(y\right)$ 在J上有定义 $f\left(I\right)\subset J$ ，在 $f\left(a\right)$ 处可微，则复合函数 $\left(g\circ f\right)\left(x\right)=g\left(f\left(x\right)\right)$ 在a处可微( $g\circ f$ 在I上有定义)，且 $\left(g\stackrel{\dot{}}{\circ }f\right)\left(a\right)=\stackrel{\dot{}}{g}\left(f\left(a\right)\right)\stackrel{\dot{}}{f}\left(a\right)$ ，若记 $u=g\left(y\right)$ ， $y=f\left(x\right)$ ，而f在I上可微g在J上可微则在I上任意点x有

$\left(g\stackrel{\dot{}}{\circ }f\right)\left(x\right)=\stackrel{\dot{}}{g}\left(f\left(x\right)\right)\stackrel{\dot{}}{f}(\; x\; )$

$\left(g\stackrel{\dot{}}{\circ }f\right)\left(x\right)=\left(\stackrel{\dot{}}{g}\circ f\right)\left(x\right)\stackrel{\dot{}}{f}(\; x\; )$

$\frac{\text{d}u}{\text{d}x}=\frac{\text{d}u}{\text{d}y}\cdot \frac{\text{d}y}{\text{d}x}$

3. 主要结果

假设 $x_i\left(t\right)$ ， $y_i\left(t\right)$ 分别是驱动系统和响应系统的任意两个解，接着令

$e_i\left(t\right)=x_i\left(t\right)-y_i(\; t\; )$

那么误差系统可以表示为：

$\begin{array}{l}\stackrel{\dot{}}{e}\left(t\right)=-o_i{e}_i\left(t\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{a}_{ij}}\left({\vartheta }_j\left(t\right)-{\mu }_j\left(t\right)\right)+{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\vartheta }_j\left(t-\rho \left(t\right)\right)}\\ +{\displaystyle \underset{j=1}{\overset{n}{\sum }}{c}_{ij}{\mu }_j\left(t-\rho \left(t\right)\right)}-u_i\left(t\right),i=1,2,\cdots ,n.\end{array}$ (3.1)

定理3.1如果假设1~3成立，那么驱动系统和响应系统通过下列控制器实现指数同步：

$u_i\left(t\right)=s_i{e}_i\left(t\right)-z_{i}sign\left(e_i\left(t\right)\right),x=1,2,3,4.$ (3.2)

$s_i\ge -O+\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}+ϵ,ϵ>0,z_i\ge A_i+B_i,H=diag\left(h_1,\cdots ,h_n\right),$

$\bar{A}=\left|A\right|H,\left|A\right|={\left(\left|a_{ij}\right|\right)}_{n\times n},A_i=\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|a_{ij}\right|g_i,\bar{c}=\left|c\right|H,\left|c\right|={\left(\left|c_{ij}\right|\right)}_{n\times n},B_i=\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\left|c_{ij}\right|g_i,i=1,2,\cdots ,n.$

因为Lyapunov泛函的基本思路是通过系统状态方程的解来判别系统的的稳定性，所以为了得到全局指数同步我们构造Lyapunov泛函。

证明：构造Lyapunov泛函

$V_1\left(t\right)=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{e}_i^2\left(t\right)}+\frac{1}{2\left(1-{\rho }^{*}\right)}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle {\int }_{t-\rho \left(t\right)}^t{e}_i^2\left(s\right)\text{d}s}}$ (3.3)

计算 $V_1\left(t\right)$ 沿着误差系统(3.1)轨迹的导数，

$\begin{array}{c}{\stackrel{\dot{}}{V}}_1\left(t\right)\le {\displaystyle \underset{i=1}{\overset{n}{\sum }}{o}_i{e}_i^2\left(t\right)}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{e}_i\left(t\right)a_{ij}\left({\vartheta }_j\left(t\right)-{\eta }_j\left(t\right)\right)}}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}{\vartheta }_j\left(t-\rho \left(t\right)\right)\right|}}\\ -{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}{\mu }_j\left(t-\rho \left(t\right)\right)\right|}}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{s}_i{e}_i^2\left(t\right)}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{z}_i\left|e_i\left(t\right)\right|\cdot sign\left(e_i\left(t\right)\right)}\\ +\frac{1}{2\left(1-{\rho }^{*}\right)}\left[{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(e_i^2\left(t\right)-e_i^2\left(t-\rho \left(t\right)\right)\right)}\right]\end{array}$ (3.4)

接下来证明不等式右边，通过不等式的放缩，并且根据假设2进行逐项证明，

$\begin{array}{c}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{e}_i\left(t\right)a_{ij}\left({\vartheta }_j\left(t\right)-{\mu }_j\left(t\right)\right)}}\le {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|a_{ij}\right|\left|{\vartheta }_j\left(t\right)-{\mu }_j\left(t\right)\right|}}\\ \le {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|a_{ij}\right|\left(h_j\left|e_j\left(t\right)\right|+g_i\right)}}\\ ={\left|e\left(t\right)\right|}^{\text{T}}\left|A\right|H\left|e\left(t\right)\right|+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|a_{ij}\right|g_i}}\\ \le \Vert \bar{A}\Vert e^{\text{T}}\left(t\right)e\left(t\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{A}_i\left|e_i\left(t\right)\right|}\end{array}$ (3.5)

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}{\vartheta }_j\left(t-\rho \left(t\right)\right)\right|}}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}{\mu }_j\left(t-\rho \left(t\right)\right)\right|}}\\ \le {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}\right|\left|{\vartheta }_j\left(t-\rho \left(t\right)\right)-{\mu }_j\left(t-\rho \left(t\right)\right)\right|}}\\ \le {\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|e_i\left(t\right)\right|\left|c_{ij}\right|\left(h_i\left|e_j\left(t-\rho \left(t\right)\right)\right|+g_i\right)}}\\ =e^{\text{T}}\left(t\right)\left|c\right|H\left|e\left(t-\rho \left(t\right)\right)\right|+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{B}_i\left|e_i\left(t\right)\right|}\\ \le \frac{1}{2}{\Vert \bar{c}\Vert }^2{\left|e\left(t\right)\right|}^{\text{T}}\left|e\left(t\right)\right|+\frac{1}{2}{e}^{\text{T}}\left(t\right)\left(t-\rho \left(t\right)\right)e\left(t\right)\left(t-\rho \left(t\right)\right)+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{B}_i\left|e_i\left(t\right)\right|}\end{array}$ (3.6)

将(3.5)和(3.6)带入(3.4)

$\begin{array}{c}{\stackrel{\dot{}}{V}}_1\left(t\right)\le e^{\text{T}}\left(t\right)\left[-O+\left(\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}\right)I_n-S\right]e\left(t\right)\\ -{\displaystyle {\sum }_{i=1}^n{z}_i\left|e_i\left(t\right)\right|}+{\displaystyle {\sum }_{i=1}^n{A}_i\left|e_i\left(t\right)\right|}+{\displaystyle {\sum }_{i=1}^n{B}_i\left|e_i\left(t\right)\right|}\end{array}$ (3.7)

由 $S_i\ge A_i+B_i$ 和(3.7)可知

${\stackrel{\dot{}}{V}}_1\left(t\right)+ϵe^{\text{T}}\left(t\right)e\left(t\right)\le e^{\text{T}}\left(t\right)\left[-O+\left(\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}+ϵ\right)I_n-S\right]e(\; t\; )$

这里 $s_i\ge -o_i+\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}+ϵ$ ，所以可以得到

${\stackrel{\dot{}}{V}}_1\left(t\right)+ϵe^{\text{T}}\left(t\right)e\left(t\right)\le 0$ (3.8)

结合(3.3)可以得到

$\begin{array}{c}{e}^{\text{T}}\left(t\right)e\left(t\right)\le 2V_1\left(t\right)=2V_1\left(0\right)+2{\displaystyle {\int }_0^t\stackrel{\dot{}}{v}\left(s\right)\text{d}s}\\ \le 2V_1\left(0\right)-2ϵ{\displaystyle {\int }_0^t{e}^{\text{T}}\left(s\right)e\left(s\right)\text{d}s}\end{array}$

根据引理2.1可知：

$e^{\text{T}}\left(t\right)e\left(t\right)\le 2V_1\left(0\right){\text{e}}^{-2ϵt}$

$\Vert e\left(t\right)\Vert \le \sqrt{\frac{2-{\rho }^{*}}{1-{\rho }^{*}}}{\text{e}}^{-2ϵt}$

由初值问题可知：

$\Vert e\left(t\right)\Vert \le \underset{-\rho \le s\le 0}{\sup }\Vert \phi \left(t\right)-\Phi \left(t\right)\Vert$

满足 $M\ge 1$ ，那么

$\Vert x\left(t\right)-y\left(t\right)\Vert \le M\underset{-\rho \le s\le 0}{\sup }\Vert \phi \left(s\right)-\Phi \left(s\right)\Vert {\text{e}}^{-ϵt}$

可以满足定义2.4，所以在不连续状态控制器(3.2)的控制下可以得到驱动系统和响应系统的全局指数同步。

4. 数值实验

本文的数值实验分为两个部分，第一个部分结合相关假设和初值问题计算控制器相关系数，最终确定了控制器模型；第二部分通过曲线变化图分析了在控制器作用下全局指数同步的效果。

例4.1当 $n=2$ 时，驱动系统和响应系统设置如下参数：

$\begin{array}{l}O=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),A=\left(\begin{array}{cc}3.8& -1\\ -2.1& 3.3\end{array}\right),B=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),C=\left(\begin{array}{cc}-2.7& -0.8\\ -3.1& -4.3\end{array}\right),\\ D=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),I={\left(0.1,0.1\right)}^{\text{T}},\rho \left(t\right)=\frac{{\text{e}}^t}{1+{\text{e}}^t},v={\left(0,1\right)}^{\text{T}}\end{array}$

激活函数设置为：

$f_i\left(x_i\left(t\right)\right)=\{\begin{array}{l}\tanh \left(x_i\left(t\right)\right)-0.04,x_i\ge 0,\\ \tanh \left(x_i\left(t\right)\right)+0.03,x_i\le 0,\end{array}i=1,2$ (4.1)

假设1和假设2满足 $h_i=1,g_i=0.06,\rho =1,{\rho }^{*}=0.2,ϵ=0.2,i=1,2$

$s_i\ge -o_i+\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}+ϵ$

$s_i=52.04345$

$A_i+B_i=0.498<z_1=0.5$

$A_i+B_i=0.768<z_2=0.8$

$s_i=53>-o_i+\Vert \bar{A}\Vert +\frac{1}{2}{\Vert \bar{c}\Vert }^2+\frac{1}{2\left(1-{\rho }^{*}\right)}+ϵ=52.04345,i=1,2$

不连续反馈控制器设计如下：

$\{\begin{array}{l}{u}_1\left(t\right)=53e_1\left(t\right)-0.5sign\left(e_1\left(t\right)\right)\\ u_2\left(t\right)=53e_2\left(t\right)-0.8sign\left(e_2\left(t\right)\right)\end{array}$ (4.2)

所有的条件满足定理3.1，驱动系统和响应系统在控制器(式4.2)的作用下达到全局指数同步，由初值定理，给定驱动系统和响应系统的初值分别为：

$x\left(s\right)={\left(0.4,-0.2\right)}^{\text{T}},y\left(s\right)={\left(0.1,-0.5\right)}^{\text{T}},s\in \left[-1,0\right]$

通过实验图1可以看出，本文设计的控制器可以使驱动和响应系统达到全局指数同步的效果。

Figure 1. Global exponential synchronization of x and y

图1. x和y的全局指数同步效果图

接下来是误差系统的曲线变化图。

从图2中可以看出，在本文设计的控制器作用下，误差在短时间内可以无限逼近于零。

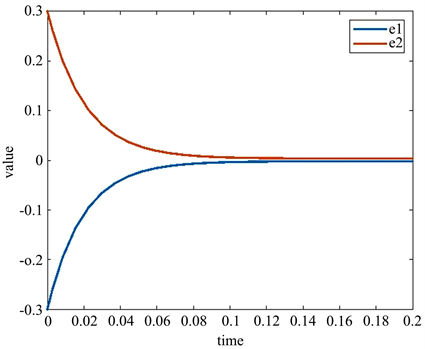
Figure 2. Global exponential synchronization effect of e

图2. e的全局指数同步效果图

5. 结论

本文主要研究了时滞递归神经网络的全局指数同步问题。首先，本文对响应系统设计了一个新的控制器；其次，从理论上和数值上证明了该控制器能够使驱动系统和响应系统实现全局指数同步；最后，通过算例进行了数值模拟，验证了理论结果的有效性。本文的数值实验是在时滞微分方程的基础上对驱动模型增加了时滞前后的模板元素，并且设计了控制器，得到了驱动系统和响应系统；通过误差分析，构造了误差系统；在设定驱动和响应系统的初始值和时间延迟函数后，分别绘制出了驱动和响应系统达到全局指数同步和误差系统的曲线图。下一步将继续对分数阶时滞递归神经网络的多稳定性进行研究。