Frobenius扩张下的(F,A)-Gorenstein平坦模

doi:10.12677/PM.2023.136159

期刊菜单

Frobenius扩张下的(F,A)-Gorenstein平坦模
(F,A)-Gorenstein Flat Modules under Frobenius Extension

DOI: 10.12677/PM.2023.136159, PDF, HTML, XML,
作者: 魏玉娟^*, 周彩霞：西北师范大学数学与统计学院，甘肃兰州
关键词: Frobenius扩张；(F；A)-Gorenstein平坦模；(F；A)-Gorenstein平坦维数；Frobenius Extensin； (F；A)-Gorenstein Flat Module； (F；A)-Gorenstein Flat Dimension

摘要: 设R⊆S是环的Frobenius扩张，M是任意左S-模，假设A是右R-模的类，B是右S-模的类，且GF_(F,B)关于扩张封闭，I(S^OP)⊆B, 在一些条件下证明了M是(F,B)-Gorenstein平坦左S-模当且仅当M是(F,A)-Gorenstein平坦左R-模当且仅当S⊗_RM是(F,B)-Gorenstein平坦左S-模。

Abstract: Let R⊆S be a Frobenius extensin of rings, M be any left S-modules. Let A be class of right R-modules and B be class of right S-modules. GF_(F,B) be closed by extension, I(S^OP)⊆B, under some conditions proved that M be (F,B)-Gorenstein flat left S-modules if and only if M be (F,A)-Gorenstein flat left S-modules if and only if S⊗_RM be (F,B)-Gorenstein flat left S-modules.

文章引用：魏玉娟, 周彩霞. Frobenius扩张下的(F,A)-Gorenstein平坦模[J]. 理论数学, 2023, 13(6): 1571-1577. https://doi.org/10.12677/PM.2023.136159

1. 引言

作为平坦模的推广，1993年，Overtoun等 [1] 引入了Gorenstein平坦模的概念，研究了其性质。2009年，Holm和Jorgensen [2] 引入了对偶对的概念。2019年，Gillespie [3] 引入了相对于对偶对 $(L, A)$ 的Gorenstein投射、内射和平坦模的概念。2022年，Becerril [4] 进一步研究了 $(F, A)$ -Gorenstein平坦模的同调性质及其维数。

1954年，Kasch [5] 引入了Frobenius扩张的概念。1960年，Nakayam，Tsuzuku [6] 和Morita [7] 对Frobenius扩张做了更深入的研究。近年来，Ren [8] 引入了可分Frobenius扩张的概念，研究了在环的Frobenius扩张下Gorenstein投射模与Gorenstein投射维数，证明了左S-模M是Gorenstein投射模当且仅当M作为左R-模也是Gorenstein投射模。2019年，Ren [9] 研究了在环的Frobenius扩张 $R \subseteq S$ 下，其中S-是右凝聚环，Gorenstein平坦模与Gorenstein平坦维数的同调不变性。

受以上结论的启发，本文研究了在环的Frobenius扩张下 $(F, A)$ -Gorenstein平坦模与 $(F, A)$ -Gorenstein平坦维数的同调不变性。

文中环R和S-均指有单位元的结合环，模均指酉模。R-模(或者S-模)表示所有的左R-模(或者左S-模)。R^op-模(或者S^op-模)表示所有的右R-模(或者右S-模)。对任意的环R， $M o d (R)$ 表示所有左R-模的范畴， $M o d (R^{o p})$ 表示所有右R-模的范畴。 $I (R)$ 表示所有内射左R-模构成的类。 $F (R)$ 表示所有平坦左R-模构成的类。

在本文中， $A$ 表示所有右R-模构成的类， $B$ 表示所有右S-模构成的类，且 $I (S^{o p}) \subseteq B$ 。

2. $(F, A)$ -Gorenstein平坦模

定义2.1 ( [9] 定义2.1)称 $R \subseteq S$ 是环的Frobenius扩张，如果满足下面五条等价条件中的一条

1) 函子 $S \otimes_{R} -$ 和 $H o m_{R} (S, -)$ 是自然等价的；

2) 函子 $- \otimes_{R} S$ 和 $H o m_{R^{o p}} (S, -)$ 是自然等价的；

3) ${}_{R}S$ 是有限生成投射模，且 ${}_{S}S_{R} ≅ H o m_{R} ({}_{R}S_{S}, R)$ ；

4) $S_{R}$ 是有限生成投射模，且 ${}_{R}S_{S} ≅ H o m_{R} ({}_{S}S_{R}, R)$ ；

5) 存在R-同态 $ξ : S \to R$ 和 $X_{i}, Y_{i} \in S$ ，使得对任意 $s \in S$ ， $\sum_{i} X_{i} ξ (Y_{i} s) = s$ 和 $\sum_{i} ξ (s X_{i}) Y_{i} = s$ 。

定义2.2 设M是左R-模，称M是 $(F, A)$ -Gorenstein平坦模，如果存在平坦左R-模的正合列

$F : \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$ ，

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $A \in A$ ， $A \otimes_{R} F$ 正合。

通常，我们将 $(F, A)$ -Gorenstein平坦模类记为 $G F_{(F, A)} (R)$ 。

引理2.3 设 $R \subseteq S$ 是环的Frobenius扩张，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

若M是 $(F, B)$ -Gorenstein平坦左S-模，则M也是 $(F, A)$ -Gorenstein平坦左R-模。

证明设M是 $(F, B)$ -Gorenstein平坦左S-模，则存在平坦左S-模的正合复形

$F = \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$ ，

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $B \in B$ ， $B \otimes_{S} F$ 是正合的。因为任意平坦左S-模都是平坦左R-模，所以F是平坦左R-模的正合复形。

令 $A \in A \subseteq M o d (R^{o p})$ ，因为 $A \otimes_{R} S ≅ H o m_{R^{O P}} (S, A)$ ，且 $H o m_{R^{O P}} (S, A)$ 是右S-模，所以 $H o m_{R^{O P}} (S, A) \otimes_{S} F$ 正合，又由同构 $A \otimes_{R} F ≅ A \otimes_{R} S \otimes_{S} F ≅ H o m_{R^{O P}} (S, A) \otimes_{S} F$ 知， $A \otimes_{R} F$ 是正合的，所以M是 $(F, A)$ -Gorenstein平坦左R-模。

引理2.4 设 $R \subseteq S$ 是环的Frobenius扩张，M是任意左S-模，假设以下成立：

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

若M是 $(F, A)$ -Gorenstein平坦左R-模，则 $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模。

证明设M是 $(F, A)$ -Gorenstein平坦左R-模，则存在平坦左R-模的正合复形

$F : \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $A \in A$ ， $A \otimes_{R} F$ 正合。由( [10] 定理2.1.13)，知 $S \otimes_{R} F$ 是平坦左S-模的正合复形，且 $S \otimes_{R} M ≅ K e r (S \otimes_{R} F^{0} \to S \otimes_{R} F^{1})$ 。对任意 $B \in B$ ，由同构 $B \otimes_{R} F ≅ B \otimes_{S} S \otimes_{R} F$ 知， $B \otimes_{S} S \otimes_{R} F$ 正合，因此 $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模。

引理2.5 ( [4] Lemma 3.11)设 $A \subseteq M o d (R^{o p})$ ， $I (R^{O P}) \subseteq A$ ，以下等价

1) $G F_{(F, A)}$ 关于扩张封闭；

2) $G F_{(F, A)}$ 是预可解的；

3) $0 \to G_{1} \to G_{0} \to M \to 0$ 是左R-模的正合序列，其中 $G_{0}, G_{1} \in G F_{(F, A)}$ ，如果对任意 $A \in A$ ， $T o r_{1}^{R} (A, M) = 0$ ，则 $M \in G F_{(F, A)}$ 。

命题2.6 若 $G F_{(F, A)}$ 关于扩张封闭，且 $I (R^{O P}) \subseteq A$ ，则 $G F_{(F, A)}$ 关于直和和直和项封闭。

命题2.7 设 $R \subseteq S$ 是环的Frobenius扩张，L是任意左S-模， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，假设以下成立

1) 对任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 对任意 $B \in B$ ， $B \in A$ ；

3) 对任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则L是 $(F, A)$ -Gorenstein平坦左R-模，当且仅当 $S \otimes_{R} L$ 是 $(F, B)$ -Gorenstein平坦左S-模。

证明 $\Rightarrow$ )由引理2.4易知。

$\Leftarrow$ )若 $S \otimes_{R} L$ 是 $(F, B)$ -Gorenstein平坦左S-模，由引理2.3知， $S \otimes_{R} L$ 也是 $(F, A)$ -Gorenstein平坦左R-模，设L是左S-模，则有自然满同态 $π : S \otimes_{R} L \to L$ ， $π (s \otimes l) = s l$ ，当看作R-同态时， $π$ 可裂，因此 ${}_{R}L$ 是 ${}_{R}{(S \otimes_{R} L)}$ 的直和项，又由命题2.6知 $(F, A)$ -Gorenstein平坦左R-模关于直和项封闭，所以L是 $(F, A)$ -Gorenstein平坦左R-模。

命题2.8 设M是左R-模，以下等价：

1) M是 $(F, A)$ -Gorenstein平坦模；

2) 对任意 $A \in A$ 及整数 $i \geq 1$ ， $T o r_{R}^{i} (A, M) = 0$ ，且M存在 $A \otimes_{R} -$ 正合的右平坦分解；

3) 存在短正合序列 $0 \to M \to F \to K \to 0$ ，其中 $F \in F (R)$ ，则 $K \in G F_{(F, A)}$ 。

证明 (1) $\Rightarrow$ (2)易得。

(3) $\Rightarrow$ (2)因为 $K \in G F_{(F, A)}$ ，所以对任意 $A \in A$ 及整数 $i \geq 1$ ， $T o r_{R}^{i} (A, K) = 0$ ，且K存在 $A \otimes_{R} -$ 正合的

右平坦分解，

$0 \to K \to F_{0} \to F_{1} \to \dots$ ， ①

将短正合序列 $0 \to M \to F \to K \to 0$ 与正合序列①连接起来，存在M的一个 $A \otimes_{R} -$ 正合的右平坦分

解，

$0 \to M \to F \to F_{0} \to F_{1} \to \dots$ ， ②

将 $A \otimes_{R} -$ 作用于短正合序列 $0 \to M \to F \to K \to 0$ ，可得长正合序列

$\dots \to T o r_{R}^{i + 1} (A, F) \to T o r_{R}^{i + 1} (A, K) \to T o r_{R}^{i} (A, M) \to T o r_{R}^{i} (A, F) \to T o r_{R}^{i} (A, K) \to \dots$ ，

从而 $T o r_{R}^{i + 1} (A, K) ≅ T o r_{R}^{i} (A, M) = 0$ 。

定理2.9 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则M是 $(ℱ, ℬ) -$ Gorenstein平坦左S-模，当且仅当M是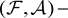Gorenstein平坦左R-模。

证明 $\Rightarrow$ )显然。

$\Leftarrow$ )设M是 $(F, A)$ -Gorenstein平坦左R-模，则对任意 $A \in A$ 及整数 $i > 0$ ， $T o r_{i}^{R} (A, M) = 0$ 。由于对任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项，因此由同构

$T o r_{i}^{S} (H o m_{R^{o p}} (S, B), M) ≅ T o r_{i}^{S} (B \otimes_{R} S, M) ≅ T o r_{i}^{R} (B, M) = 0$

可知 $T o r_{i}^{S} (B, M) = 0$ 。

由命题2.8可知，我们只需要构造 ${}_{S}M$ 的向右的一个平坦分解，由引理2.4知， $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模，又因 $S \otimes_{R} M ≅ H o m_{R} (S, M)$ ，所以存在左S-模的短正合序列

$0 \to H o m_{R} (S, M) \overset{f}{\to} F^{0} \to K \to 0$

其中 $F^{0}$ 是平坦模，K是 $(F, B)$ -Gorenstein平坦左S-模，另外，有S-模单同态 $φ : M \to H o m_{R} (S, M)$ ， $φ (m) (s) = s m$ ，将 $φ$ 限制在R-同态上， $φ$ 可裂，于是存在 $φ^{'} : H o m_{R} (S, M) \to M$ ，使得 $φ^{'} φ = 1_{M}$ ，考虑左S-模的短正合序列

$0 \to M \overset{f φ}{\to} F^{0} \to K^{0} \to 0$

其中 $K^{0} = C o k e r (f φ)$ 。由引理2.3知，K是 $(F, A)$ -Gorenstein平坦左R-模，则对任意 $A_{1} \in A$ 及整数 $i > 0$ ， $T o r_{i}^{R} (A_{1}, K) = 0$ 。从而 $A_{1} \otimes_{R} f : A_{1} \otimes_{R} H o m_{R} (S, M) \to A_{1} \otimes_{R} F^{0}$ 是单同态，同时， $A_{1} \otimes_{R} φ : A_{1} \otimes_{R} M \to A_{1} \otimes_{R} H o m_{R} (S, M)$ 也是单同态，因此序列

$0 \to A_{1} \otimes_{R} M \to A_{1} \otimes_{R} F^{0} \to A_{1} \otimes_{R} K^{0} \to 0$

是正合的，故 $T o r_{1}^{R} (A_{1}, K^{0}) = 0$ ，从而由引理2.5可得， $K^{0}$ 是 $(F, A)$ -Gorenstein平坦左R-模。用类似的方法，我们可以证得对任意 $B \in B$ ， $T o r_{1}^{S} (B, K^{0}) = 0$ ，从而序列

$0 \to B \otimes_{S} M \to B \otimes_{S} F^{0} \to B \otimes_{S} K^{0} \to 0$

是正合的。

对 $K^{0}$ 重复以上步骤，可以得到一个在函子 $B \otimes_{S} -$ 作用后依旧保持正合的短正合序列

$0 \to K^{0} \to F^{1} \to K^{1} \to 0$ ，

其中 $F^{1}$ 是平坦模， $K^{1}$ 作为R-模是 $(F, A)$ -Gorenstein平坦左R-模，通过归纳法，可以构造出 ${}_{S}M$ 的向右的一个平坦分解，

$0 \to M \to F^{0} \to F^{1} \to \dots$ ①

其中 $F^{i}$ 是平坦模，且对任意 $B \in B$ ，序列①在函子 $B \otimes_{S} -$ 的作用下保持正合。因此M是 $(F, B)$ -Gorenstein平坦左S-模。

3. $(F, A)$ -Gorenstein平坦维数

定义3.1 设M是任意左R-模，定义M的 $(F, A)$ -Gorenstein平坦维数为M的 $(F, A)$ -Gorenstein平坦维数的最短长度，即 $G f d_{(F, A)} (M) \leq n$ 当且仅当存在左R-模的正合序列

$0 \to L_{n} \to L_{n - 1} \to \dots \to L_{0} \to M \to 0$

其中n是非负整数， $L_{i} (i = 0, 1, \dots, n)$ 是 $(F, A)$ -Gorenstein平坦模。

如果这样的n不存在，则 $G f d_{(F, A)} (M) = \infty$ 。

引理3.2 由( [4] 定理3.12)可得 $(F, A)$ -Gorenstein平坦维数的另一种定义

$G f d_{(F, A)} (M) = \sup {i \in N | 存在 A \in A, 使得 T o r_{i}^{R} (A, M) = 0}$

定理3.3 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $G f d_{(F, B)} (M) < \infty$ ， $I (R^{O P}) \subseteq B$ ，M是左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

证明由引理2.3知，任意 $(F, B)$ -Gorenstein平坦左S-模都是 $(F, A)$ -Gorenstein平坦左R-模，则 $G f d_{(F, A)} (M) \leq G f d_{(F, B)} (M)$ 。下面证 $G f d_{(F, A)} (M) \geq G f d_{(F, B)} (M)$ ，设 $G f d_{(F, A)} (M) = n < \infty$ ，由引理3.2，只需证对于任意 $B \in B$ 及整数 $i > n$ ， $T o r_{i}^{S} (B, M) = 0$ ，又因对任意 $B \in B$ ， $B \in A$ ，所以 $T o r_{i}^{R} (B, M) = 0$ 。因此 $T o r_{i}^{S} (B \otimes_{R} S, M) ≅ T o r_{i}^{R} (B, M) = 0$ ，另外，由于对任意 $B \in B$ ，B是S-模 $H o m_{R^{o p}} (S, B)$ 的直和项，且 $H o m_{R^{o p}} (S, B) ≅ B \otimes_{R} S$ ，则对任意整数 $i > n$ ， $T o r_{i}^{S} (B, M) = 0$ ，故 $G f d_{(F, B)} (M) \leq n$ 。即 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

命题3.4 若 ${(M_{i})}_{i \in I}$ 是一族左R-模， $G F_{(F, A)}$ 关于扩张封闭， $I (R^{O P}) \subseteq A$ ，则

$G f d_{(F, A)} (\oplus_{I} M_{i}) = \sup {G f d_{(F, A)} (M_{i}) | i \in I}$ 。

证明类似文献 [11] 命题3.11可证。

在定理3.3中，我们需要 $G f d_{(F, B)} (M) < \infty$ ，接下来我们研究在什么情况下，任意左S-模M的 $(F, B)$ -Gorenstein平坦维数沿着环的Frobenius扩张是传递的。

命题3.5 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则

a) 若M是左R-模，则 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ ；

b) 若M作为左S-模，则 $G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M) = G f d_{(F, A)} (M)$ 。

证明 a)由引理2.3知，任意 $(F, B)$ -Gorenstein平坦左S-模都是 $(F, A)$ -Gorenstein平坦左R-模，则 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M)$ 。由引理1.3，易得 $G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ 。

b) 设M是左S-模，则M作为左R-模是 ${}_{R}{(S \otimes_{R} M)}$ 的直和项，由命题3.4，易得 $G f d_{(F, A)} (M) \leq G f d_{(F, A)} (S \otimes_{R} M)$ 。又由(a)知 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ ，故 $G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M) = G f d_{(F, A)} (M)$ 。

作为Frobenius代数的推广，2018年，Ren在文献 [8] 中提出了可分Frobenius扩张的概念.

定义3.6 [8] 称 $R \subseteq S$ 是环的可分Frobenius扩张，如果满足以下两条

1) $R \subseteq S$ 是环的可分扩张；

2) $R \subseteq S$ 是环的Frobenius扩张。

称环扩张 $R \subseteq S$ 是可分的，是指乘法映射 $φ : S \otimes_{R} S \to S$ $(s \otimes_{R} l \to s l)$ 是可裂满同态。

定理3.7 设 $R \subseteq S$ 是环的可分Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

证明因为 $R \subseteq S$ 是环的可分Frobenius扩张，所以 $φ : S \otimes_{R} M \to M$ $(s \otimes_{R} m \to s m)$ 是可裂满同态，故M是 $S \otimes_{R} M$ 的直和项，由命题3.4，易知 $G f d_{(F, B)} (M) \leq G f d_{(F, B)} (S \otimes_{R} M)$ ，由定理2.7可得不等式 $G f d_{(F, A)} (M) \leq G f d_{(F, B)} (M)$ ，从而由命题3.5(b)，我们有下面的不等式：

$G f d_{(F, B)} (M) = G f d_{(F, A)} (M) = G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M)$ 。

NOTES

^*第一作者。

参考文献

[1]	Overtoun, M., Enochs, E. and Jendan, O. (2011) Relative Homologocal Algebra. DeGruyter, Berlin.
[2]	Holm, H. and Jorgensen, P. (2009) Cotorsion Pairs Induced by Duality Pairs. Journal of Commutative Algebra, 1, 621-633. https://doi.org/10.1216/JCA-2009-1-4-621
[3]	Gillespie, J. (2019) Duality and Stable Module Categories. Journal of Pure and Applied Algebra, 223, 3425-3435. https://doi.org/10.1016/j.jpaa.2018.11.010
[4]	Becerril, V. (2022) -Gorenstein flat homological dimen-sions. Journal of the Korean Mathematical Society, 59, 1203-1227.
[5]	Kasch, F. (1954) Grundlagen einer Theorie der Frobeniuserweiterungen. Mathematische Annalen, 127, 453-474. https://doi.org/10.1007/BF01361137
[6]	Nakayama, T. and Tsuzuku, T. (1960) On Frobenius Extensions I. Na-goya Mathematical Journal, 17, 89-110. https://doi.org/10.1017/S0027763000002075
[7]	Morita, K. (1965) Adjoint Pairs of Functors and Frobenius Ex-tension. Science Reports of the Tokyo Kyoiku Daigaku, Section A, 9, 40-71.
[8]	Ren, W. (2018) Gorenstein Projective Modules and Frobenius Extensions. Science China Mathematics, 61, 1175-1186. https://doi.org/10.1007/s11425-017-9138-y
[9]	任伟. Gorenstein平坦模与Frobenius扩张[J]. 数学学报, 2019, 62(4): 647-652.
[10]	张睿杰. Frobenius扩张环上的n-Ding投射模[D]: [硕士学位论文]. 兰州: 西北师范大学, 2020.
[11]	Holm, H. (2004) Gorenstein Homological Dimensions. Journal of Pure and Applied Algebra, 189, 167-193. https://doi.org/10.1016/j.jpaa.2003.11.007

为你推荐

友情链接