基于改进的随机SEIR模型分析传染病的控制再生数

doi:10.12677/AAM.2023.127321

期刊菜单

基于改进的随机SEIR模型分析传染病的控制再生数
Analysis of the Controlled Regeneration Number of Infectious Diseases Based on an Improved Stochastic SEIR Model

DOI: 10.12677/AAM.2023.127321, PDF, HTML, XML, 下载: 255 浏览: 348
作者: 陈倩, 连保胜^*：武汉科技大学理学院，湖北武汉
关键词: 随机SEIR模型；决策树；最小二乘法；控制再生数随机SEIR模型；决策树；最小二乘法；控制再生数；Stochastic SEIR Model； Decision Trees； Least Squares； Controlled Regeneration Number

摘要: 目的：为了研究传染病的变化特征，提出了改进的随机SEIR模型去仿真疫情的变化。方法：该模型针对仅考虑隔离新增感染患者的模型，增加了对原本存在的潜伏者的隔离行为，完善了这个模型。并且为了可以更好地对疫情变化做出精确的模拟，在求模型参数时使用决策树对疫情过程分段，使得仿真更贴合疫情的变化过程。最后利用最小二乘法计算出参数，得到各个阶段的控制再生数。结果：在验证的部分，对随机SEIR模型进行社区核酸阳性人数HE和隔离人群核酸阳性人数HEq的精确值求解，并将其与实际数据对比，结果显示，改进随机SEIR模型可以较好地反映疫情变化。结论：疫情大概在四十天的时候开始走到拐点，而且这时期之后的控制再生数基本都小于1。通过观察控制再生数计算公式，可以发现主要是隔离率P的上升使得控制再生数小于1，所以后期疫情得到控制的原因主要是隔离率P的上升。

Abstract: Objective: In order to study the changing characteristics of the epidemic, an improved stochastic SEIR model was proposed to simulate the changes of the epidemic. Methods: The improved model adds the isolation behavior of pre-existing latent people to the original model that only considers the isolation of newly infected patients. In order to better simulate the changes of the epidemic, the decision tree is used to segment the epidemic process when finding the model parameters, so that the simulation is more in line with the change process of the epidemic. Finally, the parameters cal-culated by the least squares method are used to find the controlled regeneration number for each stage. Results: In the verification part, the random SEIR model was solved for the exact values of the number of nucleic acid positive people HE in the community and the number of nucleic acid positive people in the isolated population HEq, and compared them with the actual data, and the results showed that the random SEIR model with improved could better reflect the changes of the epidem-ic. Conclusions: The epidemic began to reach an inflection point at about forty days, and the number of controlled regeneration after this period was basically less than 1. By observing the calculation formula of the controlled regeneration number, it can be found that the increase of the isolation rate P makes the controlled regeneration number less than 1, so the reason for the control of the epidemic in the later stage is mainly the increase of the isolation rate P.

文章引用：陈倩, 连保胜. 基于改进的随机SEIR模型分析传染病的控制再生数[J]. 应用数学进展, 2023, 12(7): 3211-3224. https://doi.org/10.12677/AAM.2023.127321

1. 引言

2022年3月1日开始上海爆发了严重的新冠疫情，使得上海地区被封了一个多月，累计感染者几十万，造成了很大的损失，因此研究此次疫情很重要。

新型冠状病毒的感染过程具有潜伏期，所以可以建立含有潜伏期者的SEIR模型 [1] [2] [3] 来仿真疫情，这些模型考虑有症状的感染者、无症状的感染者 [2] [3] 以及处在潜伏期的感染者 [1] 对易感染者的传染。在疫情爆发时，政府会对疫情进行控制，所以在模型中加入了隔离 [1] [2] [3] 和核酸筛查功能，另外考虑到不确定因素，可以增加布朗运动作为扰动项 [4] ，建立随机SEIR模型。最后，模型的参数部分可以使用最小二乘法 [5] [6] 求得。

控制再生数可以描述疾病的传播，所以可以通过分析模型的控制再生数，揭示疫情的传播机理 [1] [4] [6] [7] [8] ，控制再生数大于1时疫情继续扩大，在控制再生数小于1的时候疫情转好。根据模型的不同可以建立SEIR模型的控制再生数 [1] [6] 和随机SEIR模型的控制再生数 [4] [7] ，也可以使用动态传播率 [8] 代替控制再生数，观察再生数的动态变化。

上述模型 [1] [2] [3] 对疫情有很好的仿真效果，但是他们建立的模型只考虑隔离易感染人群S和新被感染的人群，而实际的隔离措施应该是对社区人群(易感染者S、新增感染者和原本存在的潜伏者E)的隔离，所以上述模型缺少对原本存在的潜伏者E (和易感染者以及新增感染者一起作为社区人群)的隔离行为。本文基于以上模型，建立了考虑核酸筛查、无症状感染者和隔离的随机SEIR模型，该模型相对于这些模型 [1] [2] [3] ，考虑了对于原有潜伏者E的隔离行为，完善了这个模型。在求参数的部分，本文在实际情况的基础上，使用决策树将疫情分为多个时间段，使得仿真更贴合疫情的动态变化，然后使用最小二乘法求得参数，最后计算控制多个阶段的再生数分析疫情变化。

2. 模型建立

2.1. SEIR模型

根据疫情和防疫措施，建立一个考虑隔离、核酸筛查和无症感染者的随机SEIR模型。模型的具体建模如图1，其中S表示易感染者，E是潜伏的感染者，I是具有症状的发病者，W是无症状感染者，G是被隔离的人群，Eq是隔离人群中的潜伏者，H是住院患者，R是治愈者。由于只是讨论疫情的传播过程，所以模型没有考虑死亡率。

在模型中E人群是唯一的传染人群，E人群和S人群一起组成社区人群N，E人群对S人群有c的接触率和 $β$ 的感染率，所以新产生的感染者就是 $c β S E$ ；由于防疫政策，政府会隔离患者的接触者，设隔离率是p，那么S人群转移到潜伏者E的数量是 $c β (1 - p) S E$ ，社区人群N转移到隔离者G的数量是 $c p S E + p E$ ，设解封速度为 $τ$ ，则从隔离人群G解封回到社区人群N的数量是 $τ G$ ；在隔离人群G中，他们有概率为 $β$ 的可能是隔离的潜伏者Eq；政府使用核酸检测的方式来发现被感染者，而检测出的患者有确诊和无症状感染者，设模型中潜伏者以 $δ$ 的速度发病，那么从E潜伏者转移到I发病患者的数量是 $δ (E + E q)$ ，除掉发病的潜伏者，余下的潜伏者有w的概率通过核酸筛查的方式被发现，所以W无症状感染者增加的数量是 $(1 - δ) w (E + E q)$ ，最后I发病者和W无症状感染者都以 $ϑ$ 的速度转移到医院，成为住院患者H，在现有的防疫情况之下认为 $ϑ$ 是1，最后住院患者的治愈率是 $γ$ 。

由上建立SEIR模型：

${\begin{cases} \frac{d S}{d t} = - c (1 - β) p S E / N - c β S E / N + τ G \\ \frac{d G}{d t} = c p S E / N - τ G + p E \\ \frac{d E q}{d t} = c β p S E / N + p E - δ E q - (1 - δ) w E q \\ \frac{d E}{d t} = c β (1 - p) S E / N - p E - δ E - (1 - δ) w E \\ \frac{d W}{d t} = (1 - δ) w E + (1 - δ) w E q \\ \frac{d I}{d t} = δ E + δ E q \\ \frac{d H}{d t} = ϑ (I + W) \\ \frac{d R}{d t} = γ H \end{cases}$ (1)

Figure 1. Crowd conversion diagram

图1. 人群转化示意图

2.2. 随机SEIR模型

假设模型中的 $c β p$ 、 $c β (1 - p)$ 受到干扰 [4] ，所以在微分方程中加入扰动 $B_{1} (t)$ 和 $B_{2} (t)$ 、是标准布朗运动， $σ_{1}$ 和 $σ_{2}$ 是布朗运动的强度，并且令 $c β p = υ_{1}$ ， $c β (1 - p) = υ_{2}$ ，那么：

$d {\tilde{υ}}_{1} = υ_{1} d t + σ_{1} d B_{1} ( t )$

$d {\tilde{υ}}_{2} = υ_{2} d t + σ_{2} d B_{2} ( t )$

社区内的人员N包括易感染者S和潜伏者E，潜伏者人数相对较小，便于计算，认为S等于N，所以将公式(1)改写为：

${\begin{cases} d S = - c (1 - β) p E d t - c β E d t + τ G d t + σ_{1} E d B_{1} (t) \\ d G = c p E d t - τ G d t + p E d t \\ d E q = c β p E d t + p E d t - δ E q d t - (1 - δ) w E q d t + σ_{1} E d B_{1} (t) \\ d E = c β (1 - p) E d t - p E d t - δ E d t - (1 - δ) w E d t + σ_{2} E d B_{2} (t) \\ d H = δ E d t + (1 - δ) w E d t + δ E q d t + (1 - δ) w E q d t \\ d W = (1 - δ) w E d t + (1 - δ) w E q d t \\ d I = δ E d t + δ E q d t \\ d R = γ H \end{cases}$ (2)

在S = N的情况下，易感染人群S和G的具体变化在模型中就没有那么重要了，而且因为主要关注点在于社区的潜伏者数量，所以可以忽略治愈者的情况，并且可以根据实际数据分类情况，将无证感染者和确诊患者混合然后分为在社区中发现的核酸阳性人群H_E以及在隔离中发现的核酸阳性人群H_Eq。

所以为了简化模型，可以将公式(2)进一步修改，修改如下：

${\begin{cases} d E q = c β p E d t + p E d t - δ E q d t - (1 - δ) w E q d t + σ_{1} E d B_{1} (t) \\ d E = c β (1 - p) E d t - p E d t - δ E d t - (1 - δ) w E d t + σ_{2} E d B_{2} (t) \\ d H = δ E d t + (1 - δ) w E d t + δ E q d t + (1 - δ) w E q d t \\ d H_{E} = δ E q d t + (1 - δ) w E q d t \\ d H_{E q} = δ E d t + (1 - δ) w E d t \end{cases}$ (3)

公式(3)的Milstein [9] 解为公式(4)：

${\begin{cases} E q_{i + 1} = E q_{i} + (c β p E_{i} + p E_{i} - δ E q_{i} - (1 - δ) w E q_{i}) Δ t + σ_{1} E_{i} \sqrt{Δ t} ε_{1 i} + \frac{σ_{1}^{2}}{2} E_{i} Δ t (ε_{1 i}^{2} - 1) \\ E_{i + 1} = E_{i} + (c β (1 - p) E_{i} - p E_{i} - δ E_{i} - (1 - δ) w E_{i}) Δ t + σ_{2} E_{i} \sqrt{Δ t} ε_{2 i} + \frac{σ_{2}^{2}}{2} E_{i} Δ t (ε_{2 i}^{2} - 1) \\ H_{i + 1} = H_{i} + (δ E d t + (1 - δ) w E_{i} + δ E q_{i} + (1 - δ) w E q_{i}) Δ t \\ H_{E q (i + 1)} = H_{E q (i)} + (δ E q_{i} + (1 - δ) w E q_{i}) Δ t \\ H_{E (i + 1)} = H_{E (i)} + (δ E_{i} + (1 - δ) w E_{i}) Δ t \end{cases}$ (4)

3. 决策树分类

疫情的时间过长，他的各项系数如感染率、隔离率就会发生较大的改变，所以为了更好的仿真疫情的变化，根据估计的潜伏者E的变化情况，使用决策树将疫情分为多个时段，多次拟合参数。

$k_{i} = \frac{E_{i + 1}}{E_{i}}$ (5)

公式(5)可以直接反应每日的潜伏者E的变化情况，但实际的潜伏者数量无法直接获得，所以可以通过每日社区报道的核酸阳性H_E推断(数据来源于公众号：上海发布)，公式如下：

$P (H_{E} | E) = \frac{P (H_{E} E)}{P (E)} = \frac{P (H_{E})}{P (E)} = (1 - δ) w + δ$ (6)

$P (E) = \frac{P (H_{E})}{P (H_{E} | E)}$ (7)

使用公式(6)和(7)和实际的每日公布的社区核酸阳性数量，估计社区中存在的潜伏者E的数量。参数w参考危重症医学专家王辰2020年接受采访时的观点，取值0.3，发病日为7天，所以认为 $δ$ 是1/7，不稳定的社区潜伏者E的数据可以使用顺延六到七天内社区被发现的患者人数代替 [2] 。

这里使用从2022年3月1日开始到2022年5月13的每日新增数据，因为这段时间的数据较为稳定。使用python和公式(5)可以得到关于 $k_{i}$ 的折线图，如图2。

Figure 2. Line chart for k_i

图2. k_i的折线图

对疫情过程使用决策树进行分类，如图3。决策树通过计算增益来分裂节点。并且使用leaf-wise的方法，进行深度分裂，最后设置合适的阈值结束分裂节点。

增益计算公式：

$Z_{j} = \sum_{i = 1}^{n} {(k_{i} - \bar{k})}^{2} - \sum_{i = 1}^{j} {(k_{i} - \bar{q})}^{2} - \sum_{i = j + 1}^{n} {(k_{i} - \bar{h})}^{2}$

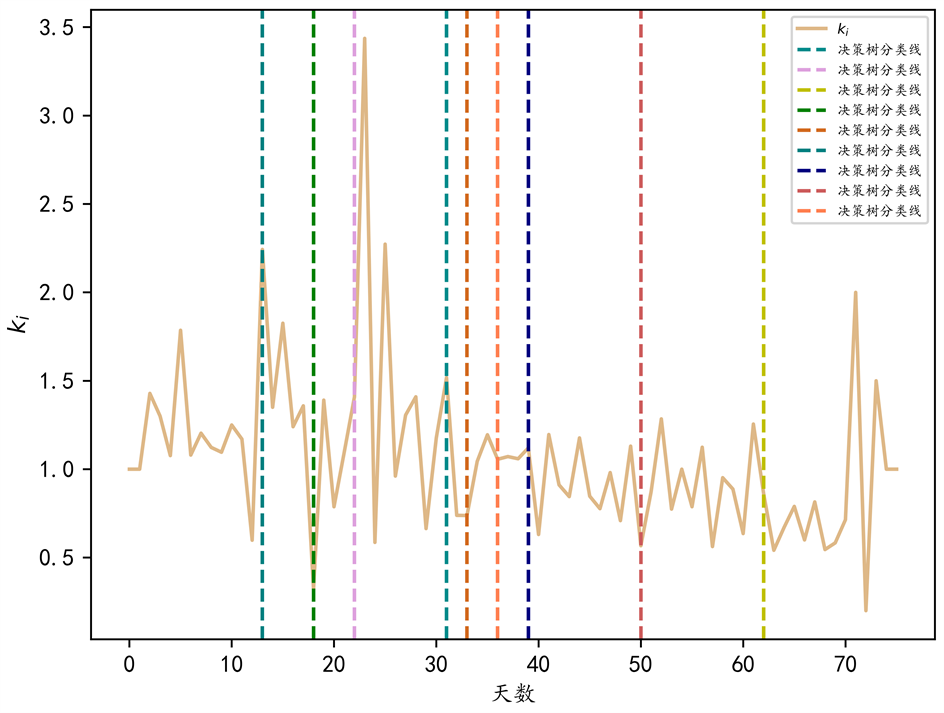
其中 $Z_{j}$ 是各个样本点的增益，其中 $\bar{k} = \frac{1}{n} \sum_{i = 1}^{n} k_{i}$ ， $\bar{q} = \frac{1}{j} \sum_{i = 1}^{j} k_{i}$ ， $\bar{h} = \frac{1}{n - j} \sum_{i = j + 1}^{n - j} k_{i}$ 。

Figure 3. Decision tree classification diagram

图3. 决策树分类图

如图3所示， $k_{i}$ 进行了多次分类，其中，在31天到39天之间，由于实际的基数值较大，波动显得较大，所以这里又进行了两次分类，另外，原本70天那里的分类由于实际数值小，影响较小，所以删去了。下面的参数将参考图3的分类效果，然后根据实际情况拟合。

4. 参数拟合与赋值

使用公式(5)和(6)能得到社区潜伏者E的数量，并且同理可得被隔离的潜伏者Eq的数量(在上海每日公布的公告中，部分隔离中的确诊患者是由无症状人员转变的，所以统计的时候减去了这一部分)。

上海公布的公告显示在3.16日开始网格化筛查核酸，所以认为从这时开始每日在社区内进行核酸筛查。网格化筛查前后期使用不同的求参数公式，后期近似社区一天一检，可以认为筛查出核酸阳性的概率 $η$ ( $η = δ + (1 - δ) w$ )是定值，前期不能确定，所以使用最小二乘法求。表1，是全文计算过程中所需要的部分参数数值。

Table 1. The parameter value

表1. 参数数值

4.1. 网格化筛查后期的求参数公式

根据公式(1)可以得到：

$E_{i + 1} = E_{i} + c β (1 - p) E_{i} - p E_{i} - δ E_{i} - (1 - δ) w E_{i}$

$E q_{i + 1} = E q_{i} + c β p E_{i} + p E_{i} - δ E q_{i} - (1 - δ) w E q_{i}$ (8)

令 $M_{i} = E_{i} + E q_{i}$ ，则：

$M_{i + 1} = M_{i} + c β E - δ M_{i} - (1 - δ) w M_{i}$ (9)

根据公式(8)和(9)可以得到：

$p_{i} = \frac{E q_{i + 1} - η E q_{i}}{E_{i} (\frac{M_{i + 1} - η M_{i}}{E_{i}} + 1)}$ (10)

其中 $η = δ + (1 - δ) w$ 。

使用最小二乘法对参数拟合，因为上海在前期疫情时并没有进行网格化筛查，所以对前后两个时期使用不同的参数求法。

在前期，根据需要求的参数，建立微分方程：

${\begin{cases} \frac{d E}{d t} = c β (1 - p) E - p E - δ E - (1 - δ) w E \\ \frac{d E q}{d t} = c β p E + p E - δ E q - (1 - δ) w E q \\ \frac{d M}{d t} = c β E - δ (E q + E) - (1 - δ) w (E q + E) \\ \frac{d H}{d t} = δ (E q + E) + (1 - δ) w (E q + E) \end{cases}$ (11)

公式(11)的雅可比矩阵为：

$J_{1} = (\begin{matrix} E & - E & - E & - E \\ 0 & E & E & - E q \\ E & 0 & 0 & - E - E q \\ 0 & 0 & 0 & E + E q \end{matrix})$

$Y_{1} = (\begin{matrix} d E & d E q & d M & H \end{matrix})$

其中 $d E = E_{i + 1} - E_{i}$ ， $d E q$ 和 $d M$ 同理，H则是每日的实际公布的阳性人数。

参数计算公式为：

$A_{1} = (X_{1}^{T} * X_{1}) * {(X_{1}^{T} * Y_{1})}^{- 1}$

解得：

$A_{1} = (\begin{matrix} A_{1} 1 & A_{1} 2 & A_{1} 3 & A_{1} 4 \end{matrix})$

其中 $A_{1} 1 = c β$ ， $A_{1} 2 = c β p$ ， $A_{1} 3 = p$ ， $A_{1} 4 = η$ ( $η = δ + (1 - δ) w$ )，具体参数如表2。

Table 2. Parameter values in the early stage of mesh screening

表2. 网格化筛查前期的参数数值

4.2. 网格化筛查后的求参数公式

在上海进行网格筛查之后，认为 $η$ 的值是稳定的，所以直接带入这个固定的数值，并且带入由公式(10)求得的离散的 $p_{i}$ 值，这样求得的数值会稳定些。

${\begin{cases} \frac{d E}{d t} = c β (1 - p) E - p E - δ E - (1 - δ) w E \\ \frac{d E q}{d t} = c β p E + p E - δ E q - (1 - δ) w E q \\ \frac{d p l}{d t} = p_{i} \\ \frac{d η l}{d t} = δ + (1 - δ) w \end{cases}$ (12)

公式(12)中 $p l$ 是累计的 $p_{i}$ ， $η l$ 是累计的 $η$ ( $η = δ + (1 - δ) w$ )。

公式(12)的雅可比矩阵为：

$J_{2} = (\begin{matrix} E & 0 & - E & - E \\ 0 & E & E & - E q \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

$Y_{2} = (\begin{matrix} d E & d E q & d p l & d η l \end{matrix})$

$W = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

W是权重矩阵，参数计算公式为：

$A_{2} = ((J_{2} * W^{T}) * J_{2}) * {((J_{2} * W^{T}) * Y_{2})}^{- 1}$

使用Matlab，使用上述公式并带入数据解出 $A_{2}$ ，可以得到参数： $A_{2} = (\begin{matrix} A_{2} 1 & A_{2} 2 & A_{2} 3 & A_{2} 4 \end{matrix})$ ，其中： $A_{2} 1 = c β (1 - p)$ ， $A_{2} 2 = c β p$ ， $A_{2} 3 = p$ ， $A_{2} 4 = η$ ( $η = δ + (1 - δ) w$ )，具体数据如表3。

Table 3. Parameter values in the later stage of mesh screening

表3. 网格化筛查后期的参数数值

4.3. 模型与实际对比

根据公式(3)得到的差分迭代方程为：

${\begin{cases} E q_{i + 1} = E q_{i} + c β p E_{i} + p E_{i} - δ E q_{i} - (1 - δ) w E q_{i} + σ_{1} E_{i} ε_{1 i} \\ E_{i + 1} = E_{i} + c β (1 - p) E_{i} - p E_{i} - δ E_{i} - (1 - δ) w E_{i} + σ_{2} E_{i} ε_{2 i} \\ H_{i + 1} = H_{i} + δ E d t + (1 - δ) w E_{i} + δ E q_{i} + (1 - δ) w E q_{i} \\ H_{E q (i + 1)} = H_{E q (i)} + δ E q_{i} + (1 - δ) w E q_{i} \\ H_{E (i + 1)} = H_{E (i)} + δ E_{i} + (1 - δ) w E_{i} \end{cases}$ (13)

利用Matlab使用公式(13)、表2和表3的参数做社区每日核酸阳性数量H_E的精确解和实际数量对比图，如图4。

Figure 4. Model simulation of the community daily number H_Eof positive nucleic acids precise solution and actual quantity comparison graph

图4. 模型仿真的社区每日核酸阳性数量H_E精确解和实际数量对比图

其中红色是真实数据，紫色是拟合数据。同理可得隔离人群的每日核酸阳性数量H_Eq的精确解和实际数量对比图，如图5。

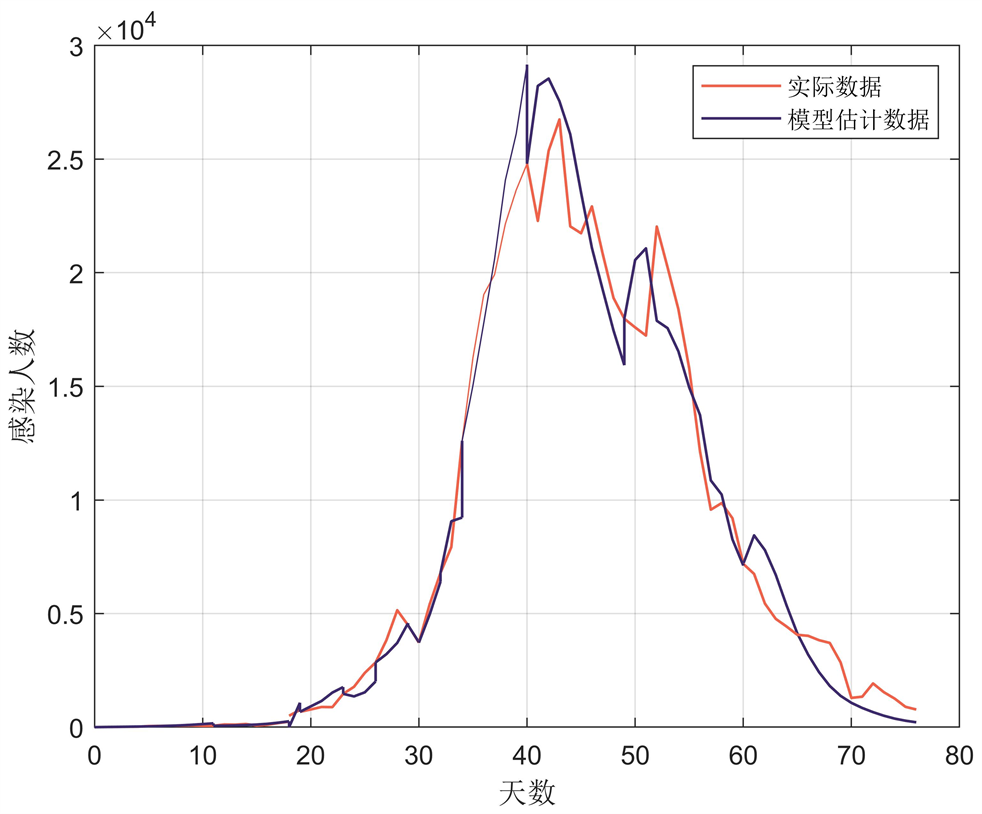
Figure 5. The daily positive number H_Eq of nucleic acids in the isolated population simulated by the model is accurately solved and compared with the actual quantity

图5. 模型仿真的隔离人群每日核酸阳性数量H_Eq精确解和实际数量对比图

其中红色是真实数据，紫色是拟合的随机SEIR模型的精确解，从图4和图5可以观察发现分段的拟合效果可以较好的反映真实的疫情变化。观察表3的参数，可以发现后期的第九和第十阶段的 $A_{2} 2$ 数值越来越大，这是由于本文是利用潜伏者E和被隔离的潜伏者Eq求参，两者的数量增减大小会影响求得的参数，而后期两者数量差距太大，所以求得的 $A_{2} 2$ 较大。

5. 控制再生数

5.1. SEIR模型的控制再生数

根据下一代矩阵法 [6] ：

$F_{E} = c β (1 - p) S E / N$

$V_{E} = p E + δ E + (1 - δ) E$

那么：

$F = c β (1 - p) S / N$

$V = p + δ + (1 - δ) w$

根据下一代矩阵法：

$R_{0} = F \cdot V^{- 1}$

所以：

$R_{0} = \frac{c β (1 - p)}{p + δ + (1 - δ) w}$ (14)

根据表2、表3和公式(14)得表4。

Table 4. The number of controlled regenerations for the SEIR model

表4. SEIR模型的控制再生数

5.2. 随机SEIR模型的控制再生数

随机SEIR模型的控制再生数 [7] 为：

$R_{0}^{S} = \frac{c β (1 - p)}{p + δ + (1 - δ) w} + \frac{σ_{2}^{2}}{2 (p + δ + (1 - δ) w)}$ (15)

使用表2、表3和公式(15)得表5。

Table 5. The number of controlled regenerations for a stochastic SEIR model

表5. 随机SEIR模型的控制再生数

SEIR模型的控制再生数和随机SEIR模型的控制再生数在第八个阶段开始小于1，表明从这时开始疫情再转好，感染人数在下降。

公式(15)是计算随机SEIR模型的控制再生数的公式， $σ$ 设置是0.1，第二项较小，所以分析影响控制再生数大小时不考虑公式的第二项。公式第一项分母中的参数 $δ + (1 - δ) w$ 在表2和表3中大小基本不变，这里为了方便计算，认为是固定值。控制再生数的大小变化主要在于参数 $c β (1 - p)$ 和参数p，所以可以根据p和 $c β$ 的大小变化分析控制再生数小于1时的变化。

在表2和表3中参数 $A_{2} 1 = c β (1 - p)$ ，而 $A_{2} 2 = c β p$ ，所以可以用这个数据大致得到 $c β$ 的数值，数据显示 $c β$ 随着时期的变化是在增大的。

控制再生数在第八个时期开始一直小于1，所以可以认为这个数值在减小。而根据上面的分析可以发现 $c β$ 是在增加的， $c β$ 的增加会使得控制再生数增加，而实际的情况是控制再生数减小，所以可以认为是另一个参数P的增加使得实际的控制再生数值减小并在第八个时期小于1。

5.3. 动态传播率

动态传播率 [8] 利用益于收集的数据信息，计算疫情每天的动态传播率。本文在文献7的基础之上将其使用的现存感染人数换为当日确定的核酸阳性患者。

$\frac{d H (t)}{d t} = q (t) H ( t )$

令 $q (t) = f (x) - 1$ ，得到：

$d \ln H (t) = (f (t) - 1) d t$

对其两边积分得到：

$H (t) = H (t_{0}) \exp {\int_{t_{0}}^{t} f (x) d x - (t - t_{0})}$ (16)

记 $a_{t} = \int_{t_{0}}^{t} f (x) d x / (t - t_{0}) - 1$ ，则(16)写为：

$H (t) = H (t_{0}) \exp {a_{t} (t - t_{0})}$ (17)

定义动态传播率： $c_{t} = 1 + a_{t}$ 。

根据公式(16)，可得：

${\hat{a}}_{t} = \frac{1}{t - t_{0}} \ln \frac{H (t)}{H ( t 0 )}$

那么：

${\hat{c}}_{t} = \frac{1}{t - t_{0}} \ln \frac{H (t)}{H (t_{0})} + 1$ ,

选取的滑窗期为3，即 $t - t_{0} = 3$ ，绘制下图，如图6。

Figure 6. Dynamic propagation rate plot

图6. 动态传播率图

从图中可以观察到动态传播率，在前半部分都是大于1的，这显示感染者人数一直都在增加，而后半部分基本都是小于1的，表明感染人数在下降，疫情趋势在减缓。

6. 疫情仿真与结论

6.1. 疫情仿真

在参数能够较好地反映疫情变化的基础上，使用公式(4)解出社区潜伏者E变化情况，其中步长为0.05，如图7。

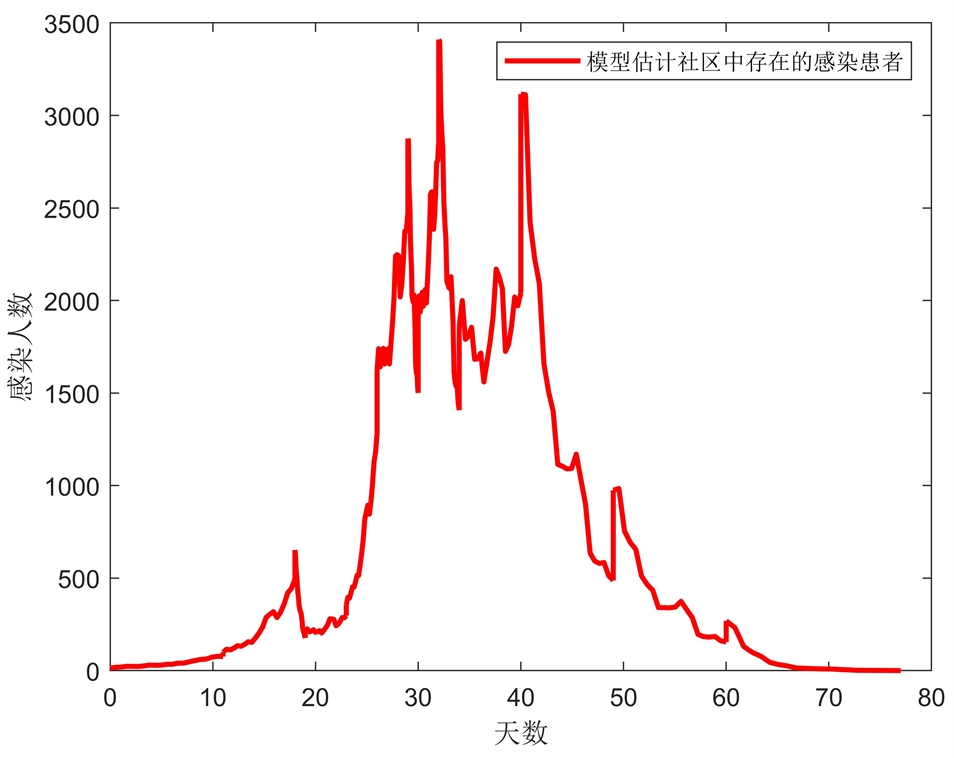
Figure 7. Community lurker E number Milstein solution number change graph

图7. 社区潜伏者E人数Milstein解的数量变化图

同理做出隔离人群中核酸阳性Eq人数的图，如图8。

Figure 8. Quantitative change plot of Milstein’s solution for Eq of infected people in isolated populations

图8. 隔离人群感染者Eq的Milstein解的数量变化图

从图7仿真的社区潜伏者人数图中观察到，以3月1日作为第一天，大约在四十天左右上海的疫情到达拐点，并且控制再生数和图8的动态传播率也是在四十天左右时小于1，所以此时是疫情的开始转变的时候。

观察表4和表5，可以发现从第八个阶段开始控制再生数都是小于1的，然后根据公式(15)及其分析可以发现主要是由于隔离率P的上升，才使得控制再生数小于1的，所以可以得出结论，此次疫情得到控制的主要在于及时隔离传染源。

6.2. 结论

传染病从古至今都是危害人民身体健康的杀手之一，因此在传染病爆发初期就要及时地监控并遏制。而通过本文建立的随机SEIR模型可以发现控制病毒传染主要有两个方面，一个是减少人与人之间的传染率，一个是隔离感染人群。第一个方面可以通过降低人与人之间的接触，从而控制接触率，达到病毒传播率的下降。第二个方面也就是及时发现并且隔离感染人员，具体的措施就是筛查人群，找到感染者及感染者的接触者。

本文通过仿真疫情并计算疫情的控制再生数，发现在此次疫情中，隔离是控制病毒传播的主要因素。而通过对模型和现实情况的具体分析，发现隔离因素可以控制感染源在社区人群中的数量，降低在社区的传染源基数，防止病毒进一步扩散。所以在以后传染病爆发时，可以着重于感染人员和潜在感染者的隔离，减少传染疾病对人民健康的伤害。

本文建立的改进的随机SEIR模型，不仅仿真了社区感染者人数，还仿真了隔离管控的感染患者人数，为其他传染病的仿真，提供了一个完善的模型。他们可以使用本文的模型，仿真社区的感染者人数和被管控的感染者人数，并且根据感染者的感染率和隔离率计算控制再生数，预测传染病的拐点。

NOTES

^*通讯作者。

参考文献

[1]	Tang, B., Wang, X., Li, Q., et al. (2020) Estimation of the Transmission Risk of the 2019-nCOV and Its Implication for Public Health Interventions. Journal of Clinical Medicine, 9, 462-475. https://doi.org/10.3390/jcm9020462
[2]	曹盛力, 冯沛华, 时朋朋. 修正SEIR传染病动力学模型应用于湖北省2019冠状病毒病(COVID-19)疫情预测和评估[J]. 浙江大学学报(医学版), 2020, 49(2): 178-184.
[3]	王霞, 唐三一, 陈勇, 等. 新型冠状病毒肺炎疫情下武汉及周边地区何时复工? 数据驱动的网络模型分析[J]. 中国科学: 数学, 2020, 50(7): 969-978.
[4]	Gray, A., Greenhalgh, D., Hu, L., et al. (2011) A Stochastic Differential Equation SIS Epidemic Model. SIAM Journal on Applied Mathematics, 71, 876-902. https://doi.org/10.1137/10081856X
[5]	须成杰, 覃开舟. 基于SEIR模型的新型冠状病毒肺炎疫情分析[J]. 计算机应用与软件, 2021, 38(12): 87-90.
[6]	于振华, 黄山阁, 杨波, 等. 新型冠状病毒肺炎传播动力学模型构建与分析[J]. 西安交通大学学报, 2022, 56(5): 43-53.
[7]	王定宇, 周少波. 一类基于心理作用的随机SIRS传染病模型[J]. 应用数学, 2022, 35(3): 731-744.
[8]	胡云鹤, 刘艳云, 吴凌霄, 等. 动态传播率模型及其在疫情分析中的应用[J]. 运筹学学报, 2020, 24(3): 27-42.
[9]	Jiang, D.Q., Yu, J.J., Ji, C.Y., et al. (2011) Asymptotic Behavior of Global Positive Solution to a Stochastic SIR Model. Mathematical and Computer Mod-elling, 54, 221-232. https://doi.org/10.1016/j.mcm.2011.02.004

为你推荐

友情链接