带有近似最优步长的随机递归梯度算法

Stochastic Recursive Gradient Algorithm with Approximately Optimal Stepsize

摘要: 在机器学习中，我们经常考虑一个目标函数是凸函数和的最小化问题。随机递归梯度算法(SARAH)是求解上面问题的一个常用方法。它允许一个简单的递归框架来更新随机梯度估计。基于SARAH方法，本文提出利用近似最优步长(AOS)去自适应地计算SARAH的步长，并将其命名为SARAH-AOS算法。针对提出的算法，我们进行了数值试验，结果表明SARAH-AOS算法对初始步长的选择并不像SARAH那样敏感。我们的算法对SARAH算法有着显著性能的改进。

Abstract: In machine learning, we often consider the problem of minimizing an objective function that is a sum of convex functions. The stochastic recursive gradient algorithm (SARAH) is a common method to solve the above problems. It allows a simple recursive framework to update stochastic gradient estimates. Based on the SARAH method, this paper, we propose to use the approximately optimal stepsize (AOS) to automatically compute stepsizes for SARAH, which leads to SARAH-AOS algorithm. For the proposed algorithm, we conduct numerical experiments, and the results show that the SARAH-AOS algorithm is not as sensitive to the selection of initial step size as SARAH. Our algorithm has a significant performance improvement over the SARAH algorithm.

1. 引言

在大规模机器学习的背景下，以下类型的优化问题被广泛考虑：

$\min P\left(\omega \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{f}_i}\left(\omega \right),$ (1)

其中每个 $f_i,i\in \left\{1,2,\cdots ,n\right\}$ 是一个具有Lipschitz连续梯度的凸函数。这类问题在监督学习应用中经常出现。 ${\left\{\left(x_i,y_i\right)\right\}}_{i=1}^n$ 为一个给定的训练集，且 $x_i\in R^d,y_i\in R^d$ ，例如，当最小二乘回归模型写成(1)，其中有 $f_i\left(\omega \right)={\left({\omega }^T{a}_i-b_i\right)}^2+\frac{\lambda }{2}{\Vert \omega \Vert }^2$ ，其中 $\Vert ·\Vert$ 表示 $l_2$ 范数。

近年来，针对问题(1)开发了许多先进的优化方法。例如梯度下降方法(GD)，特别地，GD更新迭代如下：

${\omega }_{t+1}={\omega }_t-{\eta }_t\nabla P\left({\omega }_t\right)={\omega }_t-\frac{{\eta }_t}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\nabla f_i}\left({\omega }_t\right),t=0,1,2,\cdots$ (2)

其中 ${\eta }_t$ 代表第t步迭代的学习率。GD方法虽然能达到线性收敛速度，但是当训练样本非常大时，GD方法的计算成本非常大，所以，利用GD方法求解大规模问题是不切实际的。

随机梯度下降法(SGD) [1] ，作为一种替代方法，已成为求解(1)的首选方法。在每一步，SGD均匀随机选取一个索引， $i\in \left\{1,2,\cdots ,n\right\}$ ，并将迭代更新为：

${\omega }_{t+1}={\omega }_t-{\eta }_t\nabla f_i\left({\omega }_t\right),t=0,1,2,\cdots$ (3)

这大大降低了计算成本。SGD的收敛速度比GD慢，特别是在强凸情况下，它是次线性的。然而，由于每次迭代的巨大节省和低精度解决方案足够的事实，这种权衡是有利的。

近年来，人们开发了大量提高SGD性能的方法。最流行的一种方法是梯度聚合算法 [2] ，如SAG [3] [4] 和SAGA [5] 。他们将随机梯度计算为在之前迭代中评估的随机梯度的平均值。然后它们以牺牲内存为代价来存储之前的随机梯度。随机方差衰减梯度法(SVRG) [6] 有两个循环，外层循环计算一个完整的梯度，内层循环计算方差较小的随机梯度。

AdaGrad [7] 和Adam [8] 根据历史梯度的平方和自适应地选择每个分量的步长。SVRG-BB算法 [9] 将BB步长与SVRG算法相结合，使SVRG的步长被自适应计算。随机梯度递归算法(SARAH) [10] 采用一种简单的递归框架来更新随机梯度估计。Liu等人 [11] 将SARAH与BB算法和重要性抽样策略相结合，提出了SARAH-I-BB法。刘泽显等人 [12] [13] [14] 提出了近似最优步长梯度法用来求解严格凸二次极小化问题、大规模的无约束问题。

随着随机梯度下降算法不同版本的提出，这些改进的算法从传统随机梯度下降算法上引入了很多新的思想。按照搜索方向和步长选取的方式不同，将随机梯度下降算法的改进策略大致分为动量、方差缩减、增量梯度和自适应学习率等四种类型。与SAG/SAGA相比，SARAH不需要存储过去的梯度。所以本文基于SARAH算法来进行改进。

受近似最优步长和SARAH算法成功解决问题(1)的启发。本文将近似最优步长及其思想应用于随机方差缩减梯度算法中去，将近似最优步长与SARAH结合，我们称之为SARAH-AOS方法。

2. 近似最优步长与随机递归梯度算法

在本节中，我们回顾近似最优步长与随机梯度递归算法。本节后面的叙述中 $g\left(\omega \right)=\nabla f\left(\omega \right),g_k=g\left({\omega }_k\right)$ 。

2.1. 近似最优步长

BB步长 ${\eta }_k^{BB1}={\Vert s_{k-1}\Vert }^2/s_{k-1}^T{y}_{k-1}$ 可以通过对下面的优化问题求解获得：

$\underset{\eta >0}{\min }{\Vert \frac{s_{k-1}}{\eta }I-y_{k-1}\Vert }_2^2.$

其中 $s_{k-1}={\omega }_k-{\omega }_{k-1},y_{k-1}=\nabla f\left({\omega }_k\right)-\nabla f\left({\omega }_{k-1}\right)$ 。

如果考虑线搜索函数 $f\left({\omega }_k-\eta g_k\right)$ 的二次近似模型：

${\varphi }_k\left(\eta \right)=f\left({\omega }_k\right)-\eta g_k^T{g}_k+\frac{1}{2}{\eta }^2{g}_k^T{B}_k{g}_k,$ (4)

其中 $B_k$ 为黑森矩阵的近似。当 $B_k=\frac{s_{k-1}^T{y}_{k-1}}{{\Vert s_{k-1}\Vert }^2}I$ 时，函数 $f\left({\omega }_k-\eta {\omega }_k\right)$ 的近似模型为 ${\varphi }_k\left(\eta \right)$ ，对 ${\varphi }_k\left(\eta \right)$ 极小化，最后能得到 ${\eta }_k^{BB1}$ ，即：

${\eta }_k^{BB1}=\arg \underset{\eta >0}{\min }\varphi \left(\eta \right).$

因此，BB步长 ${\eta }_k^{BB1}$ 是与(4)中的近似模型 ${\varphi }_k\left(\eta \right)$ 相关的近似最优步长。因为在BB方法中，标量近似矩阵 $\frac{s_{k-1}^T{y}_{k-1}}{{\Vert s_{k-1}\Vert }^2}I$ 要尽可能的去满足割线方程。所以(4)中二次近似模型是一个有效的近似。经过上面的分析，

下面给出近似最优步长的定义。

定义2.1：令 $\varphi \left(\eta \right)$ 是函数 $f\left({\omega }_k-\eta g_k\right)$ 的近似模型。一个正数 ${\omega }^{*}$ 被称为关于 $\varphi \left(\eta \right)$ 的近似最优步长，如果 ${\omega }^{*}$ 满足：

${\omega }^{*}=\arg \underset{\eta >0}{\min }\varphi \left(\eta \right).$

近似最优步长与柯西步长 ${\eta }_k^{SD}=\arg \underset{\eta >0}{\min }f\left({\omega }_k-\eta g_k\right)$ 不同，这将导致昂贵的计算成本。近似最优步长

通常易于计算，可应用于无约束优化。

2.2. 随机递归梯度算法(SARAH)

该算法的关键步骤是随机梯度估计的递归更新(SARAH更新)。

$v_t=\nabla f_{i_t}\left({\omega }_t\right)-\nabla f_{i_t}\left({\omega }_{t-1}\right)+v_{t-1},$ (5)

然后是迭代更新：

${\omega }_{t+1}={\omega }_t-\eta v_t.$ (6)

为了比较，SVRG更新可以用类似的方式编写：

$v_t=\nabla f_{i_t}\left({\omega }_t\right)-\nabla f_{i_t}\left({\omega }_0\right)+v_0.$ (7)

可以观察到，在SVRG中， $v_t$ 是梯度的无偏估计量，而对于SARAH则不是。因为：

$\mathbb{E}\left[v_t|{\mathcal{F}}_t\right]=\nabla P\left({\omega }_t\right)-\nabla P\left({\omega }_{t-1}\right)+v_{t-1}\ne \nabla P\left({\omega }_t\right).$ (8)

因此，SARAH不同于SGD和SVRG类型的方法，但以下总期望成立， $\mathbb{E}\left[v_t\right]=\mathbb{E}\left[\nabla P\left({\omega }_t\right)\right]$ 。SARAH算法与SVRG算法类似，因为这两个算法都包含两个循环。在每一个外循环中两者都需要计算一个完整的梯度，不同的地方就在于在内循环，其中SARAH算法通过在(5)中与之前的 $v_{t-1}$ 之间加减分量梯度递归地更新随机步长方向 $v_t$ 。

3. 带有近似最优步长的随机递归梯度算法

3.1. B_k的选择以及步长的确定

为了解决问题(1)，我们考虑 $f\left({\omega }_k-\eta g_k\right)$ 的二次逼近模型：

${\varphi }_k\left(\eta \right)=f\left({\omega }_k\right)-\eta g_k^T{g}_k+\frac{1}{2}{\eta }^2{g}_k^T{B}_k{g}_k.$

显然，通过最小化上述二次模型，梯度法的近似最优步长为：

${\eta }_k^{AOS}=\frac{{\Vert g_k\Vert }^2}{g_k^T{B}_k{g}_k}.$ (9)

由上式可以得出 $B_k$ 选择的好坏会直接影响到二次逼近模型的近似效果，所以如何构造出合适的 $B_k$ 非常重要。

本文利用BFGS公式对标量矩阵 ${\lambda }_{k}I=\frac{s_{k-1}^T{y}_{k-1}}{{\Vert s_{k-1}\Vert }^2}I$ 进行更新，从而得到 $B_k$ ：

$B_k={\lambda }_{k}I-\frac{{\lambda }_{k}I{s}_{k-1}{s}_{k-1}^T{\lambda }_{k}I}{s_{k-1}^T{\lambda }_{k}I{s}_{k-1}}+\frac{y_{k-1}{y}_{k-1}^T}{s_{k-1}^T{y}_{k-1}},$ (10)

将(10)代入(9)可以得到：

${\tilde{\eta }}_k^{AOS}=\frac{{\Vert g_k\Vert }^2}{{\lambda }_k\left({\Vert g_k\Vert }^2-\frac{\left(g_k^T{s}_{k-1}\right)}{{\Vert s_{k-1}\Vert }^2}\right)+\frac{{\left(g_k^T{s}_{k-1}\right)}^2}{s_{k-1}^T{y}_{k-1}}}.$ (11)

通过数值实验观察，我们可以发现 ${\tilde{\eta }}_k^{AOS}$ 位于区间 $\left[{\eta }_k^{BB2},{\eta }_k^{BB1}\right]$ 中。因此我们采用如下截断形式：

${\eta }_k^{AOS}=\min \left\{{\eta }_k^{BB1},\max \left\{{\eta }_k^{BB2},{\tilde{\eta }}_k^{AOS}\right\}\right\}.$ (12)

3.2. SARAH-AOS算法

当用SARAH求解问题(1)时，采用固定的步长η，并且η需要用户指定。并且SARAH算法对于步长η的选取非常敏感。我们提出了SARAH-AOS方法，该方法使用近似最优步长来计算步长 ${\eta }_k$ 。我们的SARAH-AOS算法在算法1中描述。SARAH和SARAH-AOS之间的区别是，后者使用近似最优步长来计算步长 ${\eta }_k$ ，而不是像SARAH那样使用前面的η。

4. 数值实验

为了支持理论分析和见解，我们提出了我们的实验验证。我们在w8a、ijcnn1、a9a三个数据集上对我们的算法进行数值实验，数据集的具体信息如表1所示。并且用SARAH-AOS算法去解决下面的两个问题。带有 $l_2$ 范数正则化的逻辑回归：

$\underset{x}{\min }F\left(x\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\log \left[1+{\text{e}}^{(-b_i{a}_i^{T}x)}\right]+}\frac{\lambda }{2}{\Vert x\Vert }_2^2,$ (13)

和带有 $l_2$ 范数正则化的平方铰链损失支持向量机：

$\underset{x}{\min }F\left(x\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\left[1-b_i{a}_i^{T}x\right]}_{+}\right)}^2+}\frac{\lambda }{2}{\Vert x\Vert }_2^2.$ (14)

Table 1. Data and model information of the experiments

表1. 实验数据和模型信息

新算法与SARAH的效果对比如图1~6所示。在图1~6中，横坐标代表迭代的次数。在图1~3中，纵坐标代表算法的次优性 $F\left({\tilde{x}}_k\right)-F\left(x^{*}\right)$ 。在图4~6中，纵坐标代表步长 ${\eta }_k$ 的变化。

在下面所有图中，虚线对应采用固定步长的SARAH算法。红色虚线表示最具调优步长的SARAH算法。蓝色虚线使用比最优步长稍大的步长，黑色虚线使用较小的固定步长。*实线对应的是具有不同初始步长的SARAH-AOS算法。例如，图1和图4中的实线分别对应于初始步长 ${\eta }_0=0.09、0.15、0.24$ 的SARAH-AOS算法。

Figure 1. Sub-optimality on w8a

图1. w8a上的次优性比较

Figure 2. Sub-optimality on a9a

图2. a9a上的次优性比较

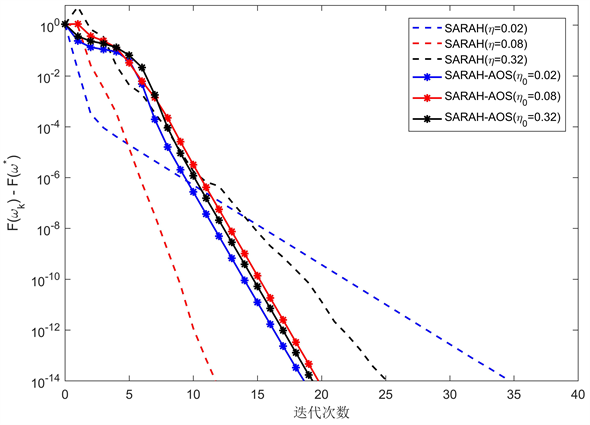
Figure 3. Sub-optimality on ijcnn1

图3. ijcnn1上的次优性比较

从图1~3我们可以看到SARAH-AOS算法始终可以达到与SARAH相同的次优性水平，且是最佳调优的步长。尽管SARAH-AOS比具有最佳调优步长的SARAH需要更多的迭代次数，但它明显优于具有其他两种步长选择的SARAH。此外，SARAH-AOS算法性能受初始步长的选择影响要明显小于SARAH算法。

Figure 4. Stepsizes on w8a

图4. w8a上的步长变化

Figure 5. Stepsizes on a9a

图5. a9a上的步长变化

Figure 6. Stepsizes on ijcnn1

图6. ijcnn1上的步长变化

5. 结论

本文提出了一种新的算法SARAH-AOS算法。在SARAH的外循环中我们采用近似最优步长自动地计算算法的步长，与采用固定步长的传统SARAH算法相比，该算法有较好的数值性能。在数值实验中，我们发现新算法能够达到与带有最调优步长的随机递归梯度下降算法相同程度的次优性。并且发现SARAH-AOS算法对于初始步长 ${\eta }_0$ 的选择并不敏感。并且SARAH-AOS算法中计算的步长最终将接近SARAH的最调优步长。因此新算法能自动生成最佳步长，所以它具有很大的实际应用潜力。数值计算结果也表明，它具有良好的数值性能。但是SARAH-AOS算法的内循环大小仍然需要用户去指定，这是该算法局限的地方。后续我们的工作将围绕这一不足点做进一步的改进。

基金项目

国家自然科学基金项目(12261019)。