求解一类时间分数阶偏微分方程的高阶格式

Solving a Class of Time-Fractional Order Par-tial Differential Equations in High Order Scheme

摘要: 本文研究了一类时间分数阶偏微分方程的数值解。首先，本文利用高阶加权本质无振荡(WENO)格式对空间变量进行离散化，使其在空间方向上达到高阶精度，因此得到一个只跟时间有关的常微分方程。接着在时间方向上应用指数和近似(SOE)时间分数阶Caputo导数，以减少内存和复杂度，达到快速计算的目的。其次，从理论上分析了WENO方法的高阶收敛性。最后通过数值实验验证了该方法的高阶精度。同时，应用该方法去数值求解含间断解的方程可以在非光滑区域保持本质无振荡，验证了该方法的有效性。

Abstract: This paper investigates the numerical solution of a class of partial differential equations of time- fractional order. Firstly, the paper discretizes the spatial variables using the higher order weighted essential no oscillation (WENO) scheme to achieve high accuracy in the spatial direction, thus ob-taining an ordinary differential equation related only to time. Then, the exponential sum approxi-mation (SOE) to the time-fractional order Caputo derivative is applied in the time direction to re-duce memory and complexity for fast computation. Next, the higher-order convergence of the WENO method is analyzed theoretically. Finally, the higher-order accuracy of the method is verified by numerical experiments. Meanwhile, applying the method to solve the equations containing inter-rupted solutions numerically is found to maintain the essence of non-oscillation in the non- smooth region, which verifies the effectiveness of the method.

1. 引言

分数阶微分方程作为传统整数阶微分方程的推广，为更好地描述粘弹性力学、异常扩散现象、记忆过程和遗传效应提供了强有力的工具，被广泛应用于科学和工程的各个领域 [1] [2] 。且由于分数算子是非局部的，它考虑了历史分布效应。在过去的几十年里，大量的应用和物理表现促进了分数阶微积分的发展。人们建立了各种分数阶偏微分方程来描述工程、科学和经济领域的现象，如非晶半导体中的载流子输运、系统识别与控制、电化学中的反常扩散、压裂电路、电极电解液界面、粘弹性、生物科学中的分数阶神经建模、混沌理论、金融学等 [3] 。

近几十年来，高阶本质无振荡格式(ENO)和WENO格式被广泛应用于求解对流–扩散偏微分方程中的双曲守恒律和对流项的近似，且它们具有守恒性好、光滑区域内的高阶精度和不连续点附近无振荡等特点。在1985年，Harten等 [4] 提出了总变分递减(TVD)准则的弱版本，为高阶ENO格式的空间重构设计了基础。1994年，Liu等 [5] 设计了一种三阶精度有限体积WENO格式。1996年，Jiang和Shu [6] 提出了求解双曲守恒律的五阶有限差分WENO格式，并分别给出了新的光滑因子和非线性权值。然后，其他许多经典的高阶数值格式，如优化WENO格式、保持单调性WENO格式、混合紧致WENO格式、鲁棒WENO格式，以及限制不连续Galerkin数值解的分级重建(HR)方法，以及中心紧致WENO (CWENO)格式等也在文献中被提出。所有这些高阶ENO和WENO格式等在求解偏微分方程的数值模拟中都是相当成功的。

最近，求解分数阶偏微分方程的高阶数值格式引起了广泛的关注。Liu等人 [7] 设计了高精度有限差分WENO格式，该格式利用保守通量差分直接逼近二阶导数。之后求解空间分数阶微分方程，Liu等人引入了直线格式 [8] 。Meerschaert和Tadieran [9] 提出了有限差分格式。2008年，Deng [10] 提出了空间和时空分数阶微分方程的有限元方法。2010年，Li和Xu [11] 提出了求解时空分数阶扩散方程的谱方法。2013年，Deng和Du [12] 将高阶有限差分WENO格式推广用于分数阶微分方程的求解，在求解不连续解的方程时可以抑制解的震荡。2021年，Zhang和Deng [13] 设计了一个新的求解含间断解的分数阶微分方程的高阶有限差分WENO格式。此外，还有许多学者对于研究新型WENO格式及WENO格式的应用 [14] [15] 做出了重要贡献，促进了该领域的蓬勃发展。据了解，目前还没有学者将WENO格式结合SOE方法求解时间分数阶偏微分方程，因此，本文将这两者结合应用求解此类方程。

本文采用有限差分WENO方法离散空间变量，建立空间高精度有限差分格式。同时为了加速时间方向上的计算，利用SOE快速逼近时间分数阶导数，相比用L1公式去逼近当前层的分数阶Caputo导数可以大幅度减少计算量。本文将主要应用WENO方法求解时间分数阶偏微分方程，通过将WENO方法和SOE逼近有效匹配从而将方程离散，并应用去求解含间断解的分数阶微分方程。

本文组织结构如下：在第2节中，介绍有限差分WENO格式分别近似空间一阶导数和两阶导数，并进行了精度分析，然后在第3节中介绍了近似时间分数阶Caputo导数的SOE方法并将时间和空间方向上的近似结合起来得到所求方程的全离散格式。第4节的数值实验验证了所提格式的有效性。第5节给出简要的总结。

2 . 空间高精度WENO有限差分格式

本文设计了一种结合SOE方法和WENO近似的有效格式，用于求解如下的时间分数阶偏微分方程(TFDE)的初边值问题：

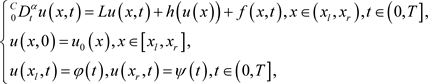(2.1)

其中L是空间变量的微分算子(线性或者非线性)， $\left(x_l,x_r\right)$ 为空间区域， $(0,T]$ 为时间区间， $u_0\left(x\right)$ 、 $\phi \left(x\right)$ 和 $\psi \left(t\right)$ 为给定的两个足够光滑的函数，Caputo导数 ${}_0{}^{C}D{}_t^{\alpha }u\left(x,t\right)$ 定义如下：

${}_0{}^{C}D{}_t^{\alpha }u\left(x,t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle {\int }_0^t\frac{\partial u\left(x,s\right)}{\partial s}\frac{1}{{\left(t-s\right)}^{\alpha }}\text{d}s},0<\alpha <1,$ (2.2)

$\Gamma (\cdot )$ 为伽玛函数。

为了构造方程(2.1)的差分格式，本文先对(2.1)右边的空间导数应用空间有限差分WENO格式离散，接下来我们详细介绍高阶WENO算法有限差分格式。

2.1. 一阶空间导数的WENO-Z有限差分格式

本文为了方便叙述，先考虑微分算子L是梯度算子的情况。记网格步长为 $\Delta x=x_{i+1}-x_i$ ，半点记为 $x_{i+\frac{1}{2}}=\frac{1}{2}\left(x_i+x_{i+1}\right)$ 。WENO方法离散空间导数，基本思想是通过线性组合低阶通量得到高阶通量。具体的方法介绍如下：

首先定义：

$v\left(x,t\right)=\frac{\partial }{\partial x}u\left(x,t\right)=f{\left(u\right)}_x,$ (2.3)

则(2.3)的半离散守恒高阶有限差分格式可以写成以下形式：

$v_j\left(t\right)=\frac{{\hat{f}}_{j+1/2}-{\hat{f}}_{j-1/2}}{\Delta x},$ (2.4)

其中 $v_j\left(t\right)$ 是对精确解的节点值 $v\left(x_j,t\right)$ 的数值近似，且数值通量 ${\hat{f}}_{j+1/2}$ 是对 $h\left(x_{j+1/2}\right)$ 的高阶近似。 $h\left(x\right)$ 的定义为 [6] ：

$f\left(u\left(x\right)\right)=\frac{1}{\Delta x}{\displaystyle {\int }_{x-\Delta x/2}^{x+\Delta x/2}h}\left(\xi \right)\text{d}\xi .$

同时，为了保持数值的稳定性，因此有必要将物理通量 $f\left(u\right)$ 分成以下两部分：

$f\left(u\right)=f^{+}\left(u\right)+f^{-}\left(u\right),$

满足 $\frac{\text{d}{f}^{+}\left(u\right)}{\text{d}u}\ge 0,\frac{\text{d}{f}^{-}\left(u\right)}{\text{d}u}\le 0$ 。在这里，我们使用最简单和最常见的Lax-Friedriches通量分裂法，其表达式为：

$f^{\pm }\left(u\right)=\frac{1}{2}\left(f\left(u\right)\pm \alpha u\right),$

其中 $\alpha =\max \left|f^{\prime }\left(u\right)\right|$ 。因此，基于 $f^{+}\left(u\right)$和 $f^{-}\left(u\right)$ ，利用WENO重构可分别得到在点 $x_{j+1/2}$ 处的 ${\hat{f}}_{j+1/2}^{+}$ 和 ${\hat{f}}_{j+1/2}^{-}$ 的值。最后，(2.4)中的 ${\hat{f}}_{j+1/2}$ 可以表示为：

${\hat{f}}_{j+1/2}={\hat{f}}_{j+1/2}^{+}+{\hat{f}}_{j+1/2}^{-},$

由(2.3)中的数值通量 $f\left(u\right)$ 满足 $f^{\prime }\left(u\right)=1\ge 0$ ，因此接下来只需要展示近似数值通量 $f^{+}\left(u\right)$ 的WENO过程。如果所有的u不都满足 $f^{\prime }\left(u\right)\ge 0$ ，则 $f^{-}\left(u\right)$ 的近似公式是 $f^{+}\left(u\right)$ 关于中点 $x_{j+1/2}$ 对称的。

对于高阶有限差分WENO格式，我们先选取一个以点 $x_{j+1/2}$ 为中心且包含 $2r-1$ 个节点的大模板 $S^{2r-1}=\left\{x_{j-r+1},\cdots ,x_{j+r-1}\right\}$ ，通过使用这 $2r-1$ 个节点，可以重构一个 $2r-1$ 阶的数值通量如下：

${\hat{f}}_{j+\frac{1}{2}}=q^{2r-1}\left(f_{j-r+1},\cdots ,f_{j+r-1}\right),$

然后将大模板 $S^{2r-1}$ 可以分成r个小模板，这些小模板都包含r个节点，分别包含的节点如下：

$S_k=\left\{x_{j+k-r+1},x_{j+k-r+2},\cdots ,x_{j+k}\right\},k=0,1,\cdots ,r-1,$

因此，在每个子模板上，我们同样可以重构一个r阶的数值通量，记为：

${\hat{f}}_{j+\frac{1}{2}}^{\left(k\right)}=q_k^r\left(f_{j+k-r+1},\cdots ,f_{j+k}\right),$

其中 $q_k^r\left(g_0,\cdots ,g_{r-1}\right)={\displaystyle \underset{l=0}{\overset{r-1}{\sum }}{a}_{k,l}^r}{g}_l$ ， $a_{k,l}^r\left(0\le k,l\le r-1\right)$ 是一些常系数。并且可以发现 ${\hat{f}}_{j+\frac{1}{2}}$ 可以由 ${\hat{f}}_{j+\frac{1}{2}}^{\left(k\right)}\left(k=0,1,\cdots ,r-1\right)$ 的线性组合得到：

$q^{2r-1}\left(f_{j-r+1},\cdots ,f_{i+r-1}\right)={\displaystyle \underset{k=0}{\overset{r-1}{\sum }}{C}_k^r}{q}_k^r\left(f_{j+k-r+1},\cdots ,f_{j+k}\right),$ (2.5)

其中 $C_k^r$ 是唯一确定的常系数，称为线性权重。

然而，线性组合格式(2.5)虽然可以获得更高阶的精度，但并不能有效地捕捉激波。基于此，本文提出的WENO算法格式如下：

${\hat{f}}_{j+1/2}={\displaystyle \underset{k=0}{\overset{r-1}{\sum }}{\omega }_k}{q}_k^r\left(f_{j+k-r+1},\cdots ,f_{j+k}\right),$

${\omega }_k\left(k=0,1,\cdots ,r-1\right)$ 为非线性权值。

为了避免间断附近的非物理振荡，在包含间断的模板上重构的多项式其对应的非线性权值应接近于0。因此本文考虑WENO-Z格式，取 $r=3$ ，其非线性权重的计算公式如下 [16] ：

${\omega }_k^{\text{z}}=\frac{{\alpha }_k^{\text{Z}}}{{\displaystyle \underset{l=0}{\overset{2}{\sum }}{\alpha }_l^{\text{z}}}},{\alpha }_k^{\text{z}}=C_k^r\left(1+{\left(\frac{{\tau }_5}{I{S}_k+ϵ}\right)}^p\right),$

其中 ${\tau }_5=\left|I{S}_0-I{S}_2\right|$ ，p取2， $ϵ={10}^{-6}$ 。 $I{S}_k$ 是模板 $S_k\left(k=0,1,\cdots ,r-1\right)$ 对应的光滑因子，本文考虑应用Jiang和Shu [6] 提出的光滑因子，其定义如下：

$I{S}_k={\displaystyle \underset{l=1}{\overset{r-1}{\sum }}{\displaystyle {\int }_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}\Delta }}{x}^{2l-1}{\left(\frac{{\partial }^l{\hat{f}}^{\left(k\right)}\left(x\right)}{{\partial }^{l}x}\right)}^2\text{d}x.$

综上就是WENO-Z差分格式的重构过程。接下来，我们继续介绍微分算子L的其他情况。

2.2. 两阶空间导数的六阶WENO格式

当微分算子 $L$ 是拉普拉斯算子时，两阶空间导数的离散本文不考虑传统的六阶WENO格式，而考虑模板空间大小不等的WENO格式。该WENO有两个优点：一是线性权重可以是任何正数，条件是它们的总和等于1；二是它在工程应用中的简单性。其构造过程详细介绍如下：

首先，空间区域的划分同2.1节，并定义：

$w\left(x,t\right)=\frac{{\partial }^2}{\partial x^2}u\left(x,t\right)=g{\left(u\right)}_{xx},$ (2.6)

得到(2.6)的半离散有限格式为：

$w_j\left(t\right)=\frac{{\hat{g}}_{j+\frac{1}{2}}-{\hat{g}}_{j-\frac{1}{2}}}{\Delta x^2},$

其中数值通量 ${\hat{g}}_{j-\frac{1}{2}}$ 的重构与重构数值通量 ${\hat{g}}_{j+\frac{1}{2}}$ 是相似的，只需模板向左平移一个网格间距即可，因此以下只介绍重构数值通量 ${\hat{g}}_{j+\frac{1}{2}}$ 的过程，可分为下面几步：

Step 1：选择一个六点大模板 $S_1=\left\{x_{j-2},x_{j-1},x_j,x_{j+1},x_{j+2},x_{j+3}\right\}$ 和两个三点小模板 $S_2=\left\{x_{j-1},x_j,x_{j+1}\right\}$ ， $S_3=\left\{x_j,x_{j+1},x_{j+2}\right\}$ ，分别得到在点 $x_{j+\frac{1}{2}}$ 的重构值为：

$\begin{array}{l}{\hat{g}}_1\left(x_{j+\frac{1}{2}}\right)=\frac{-2g\left(u_{j-2}\right)+25g\left(u_{j-1}\right)-245g\left(u_j\right)+245g\left(u_{j+1}\right)-25g\left(u_{j+2}\right)+2g\left(u_{j+3}\right)}{180},\\ {\hat{g}}_2\left(x_{j+\frac{1}{2}}\right)=g\left(u_{j+1}\right)-g\left(u_j\right),\\ {\hat{g}}_3\left(x_{j+\frac{1}{2}}\right)=g\left(u_{j+1}\right)-g\left(u_j\right).\end{array}$ (2.7)

Step 2：将 ${\hat{g}}_1\left(x_{j+\frac{1}{2}}\right)$ 改写为：

${\hat{g}}_1\left(x_{j+\frac{1}{2}}\right)={\gamma }_1\left(\frac{1}{{\gamma }_1}{\hat{g}}_1\left(x_{j+\frac{1}{2}}\right)-\frac{{\gamma }_2}{{\gamma }_1}{\hat{g}}_2\left(x_{j+\frac{1}{2}}\right)-\frac{{\gamma }_3}{{\gamma }_1}{\hat{g}}_3\left(x_{j+\frac{1}{2}}\right)\right)+{\gamma }_2{\hat{g}}_2\left(x_{j+\frac{1}{2}}\right)+{\gamma }_3{\hat{g}}_3\left(x_{j+\frac{1}{2}}\right),$ (2.8)

其中 ${\gamma }_1\ne 0$ ，且线性权重 ${\gamma }_1,{\gamma }_2,{\gamma }_3$ 可以取任意正整数满足 ${\gamma }_1+{\gamma }_2+{\gamma }_3=1$ 。

Step 3：计算光滑因子 $\widetilde{I{S}_k}\left(k=1,2,3\right)$ ，定义如下：

$\widetilde{I{S}_k}={\displaystyle \underset{n=1}{\overset{l}{\sum }}\Delta }{x}^{2n-1}{\displaystyle {\int }_{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}{\left(\frac{{\text{d}}^n}{\text{d}{x}^n}{\hat{g}}_{j+\frac{1}{2}}^{\left(k\right)}\left(x\right)\right)}^2}\text{d}x,$

其中当 $k=1$ 时， $l=4$ ， $k=2,3$ 时， $l=1$ 。得到 $\widetilde{I{S}_k}\left(k=1,2,3\right)$ 的具体表达式如下：

$\begin{array}{c}\widetilde{I{S}_1}=\frac{1}{60480}[83708g^2\left(u_{j-2}\right)+2002064g^2\left(u_{j-1}\right)+7847144g^2\left(u_j\right)-15310492g\left(u_j\right)g\left(u_{j+1}\right)\\ +7847144g^2\left(u_{j+1}\right)+7205468g\left(u_j\right)g\left(u_{j+2}\right)-7738322g\left(u_{j+1}\right)g\left(u_{j+2}\right)+2002064g^2\left(u_{j+2}\right)\\ +g\left(u_{j-2}\right)[-791699g\left(u_{j-1}\right)+1457188g\left(u_j\right)-1308130g\left(u_{j+1}\right)+574412g\left(u_{j+2}\right)-99187g\left(u_{j+3}\right)]\\ -1308130g\left(u_i\right)g\left(u_{j+3}\right)+1457188g\left(u_{j+1}\right)g\left(u_{j+3}\right)-791699g\left(u_{j+2}\right)g\left(u_{j+3}\right)+83708g^2\left(u_{j+3}\right)\\ +g\left(u_{j-1}\right)\left[-7738322g\left(u_j\right)+7205468g\left(u_{j+1}\right)-3253987g\left(u_{j+2}\right)+574412g\left(u_{j+3}\right)\right]],\end{array}$ (2.9)

$\begin{array}{c}\widetilde{I{S}_2}={\left[g\left(u_{j-1}\right)-2g\left(u_j\right)+g\left(u_{j+1}\right)\right]}^2,\\ \widetilde{I{S}_3}={\left[g\left(u_j\right)-2g\left(u_{j+1}\right)+g\left(u_{j+2}\right)\right]}^2.\end{array}$

Step 4：基于前两步的线性权重和光滑因子计算非线性权重 $\widetilde{w_k}\left(k=1,2,3\right)$ ，定义如下 [13] ：

$\widetilde{w_k}=\frac{{\hat{\omega }}_k}{{\displaystyle \underset{l=1}{\overset{3}{\sum }}{\hat{\omega }}_k}},{\hat{\omega }}_k={\gamma }_k\left(1+\frac{\tau }{\epsilon +\widetilde{I{S}_k}}\right),k=1,2,3$ (2.10)

其中 $\tau ={\left(\frac{\left|\widetilde{I{S}_1}-\widetilde{I{S}_2}\right|+\left|\widetilde{I{S}_1}-\widetilde{I{S}_3}\right|}{2}\right)}^2$ ， $\epsilon ={10}^{-6}$ 。

Step 5：把(2.8)中的线性权重换成(2.10)中的非线性权重，得到最终的数值通量重构公式：

${\hat{g}}_{i+\frac{1}{2}}\approx \widetilde{w_1}\left(\frac{1}{{\gamma }_1}{P}_1\left(x_{j+1/2}\right)-\frac{{\gamma }_2}{{\gamma }_1}{P}_2\left(x_{j+1/2}\right)-\frac{{\gamma }_3}{{\gamma }_1}{P}_3\left(x_{j+1/2}\right)\right)+\widetilde{w_2}{P}_2\left(x_{j+1/2}\right)+\widetilde{w_3}{P}_3\left(x_{j+1/2}\right).$ (2.11)

接下来，我们进行精度分析。首先将(2.9)中的光滑因子在 $g\left(u_j\right)$ 处泰勒展开得到：

$\begin{array}{c}\widetilde{I{S}_1}=\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2+\Delta x^5{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\frac{4}{3}\Delta x^6{\left(g^{‴}\left(u_j\right)\right)}^2+\frac{1}{4}\Delta x^6{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\mathcal{O}\left(\Delta x^7\right)\\ =\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2\left(1+\mathcal{O}\left(\Delta x\right)\right)=\mathcal{O}\left(\Delta x^4\right)\\ \widetilde{I{S}_2}=\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2+\frac{1}{6}\Delta x^6{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\mathcal{O}\left(\Delta x^7\right)=\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2\left(1+\mathcal{O}\left(\Delta x^2\right)\right)=\mathcal{O}\left(\Delta x^4\right),\\ \widetilde{I{S}_3}=\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2+\frac{4}{3}\Delta x^5{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\frac{4}{9}\Delta x^6{\left(g^{‴}\left(u_j\right)\right)}^2+\frac{7}{6}\Delta x^6{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\mathcal{O}\left(\Delta x^7\right)\\ =\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2(1+\mathcal{O}(\Delta x))=\mathcal{O}\left(\Delta x^4\right).\end{array}$ (2.12)

注意到 $\widetilde{I{S}_{1,3}}=C\left(1+\mathcal{O}\left(\Delta x\right)\right)$ ， $\widetilde{I{S}_2}=C\left(1+\mathcal{O}\left(\Delta x^2\right)\right)$ ，其中 $C=\Delta x^4{\left(g^{″}\left(u_j\right)\right)}^2$ ，且当 $g^{″}\left(u_j\right)\ne 0$ 时，C是一个不为0的常数。同时，由(2.12)我们还能得到：

$\begin{array}{l}\widetilde{I{S}_1}-\widetilde{I{S}_2}=\Delta x^5{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\frac{4}{3}\Delta x^6{\left(g^{‴}\left(u_j\right)\right)}^2+\frac{1}{12}\Delta x^6{g}^{″}\left(u_j\right)g^{‴}\text{'}\left(u_j\right)+\mathcal{O}\left(\Delta x^7\right)=\mathcal{O}\left(\Delta x^5\right)\\ \widetilde{I{S}_1}-\widetilde{I{S}_3}=-\frac{1}{3}\Delta x^5{g}^{″}\left(u_j\right)g^{‴}\left(u_j\right)+\frac{8}{9}\Delta x^6{\left(g^{‴}\left(u_j\right)\right)}^2-\frac{11}{12}\Delta x^6{g}^{″}\left(u_j\right)g^{‴}\text{'}\left(u_j\right)+\mathcal{O}\left(\Delta x^7\right)=\mathcal{O}\left(\Delta x^5\right).\end{array}$ (2.13)

因此，由(2.13)得非线性权重(2.10)中定义的参数 $\tau$ 有：

$\tau ={\left(\frac{\left|\widetilde{I{S}_1}-\widetilde{I{S}_2}\right|+\left|\widetilde{I{S}_1}-\widetilde{I{S}_3}\right|}{2}\right)}^2=\mathcal{O}\left(\Delta x^{10}\right).$ (2.14)

结合(2.12)、(2.13)、(2.14)，当满足条件 $\epsilon \le \widetilde{I{S}_k},\left(k=1,2,3\right)$ ，在光滑区域有：

$\frac{\tau }{\epsilon +\widetilde{I{S}_k}}=\mathcal{O}\left(\Delta x^6\right),$

综上(2.10)中定义的非线性权重满足空间六阶高精度的条件 $\widetilde{I{S}_k}={\gamma }_k+\mathcal{O}\left(\Delta x^6\right),\left(k=1,2,3\right)$ 。

以上我们介绍了空间方向上的WENO高阶近似，接下来我们介绍时间方向上的近似并得到方程(2.1)的全离散格式。

3 . 全离散WENO-SOE格式

考虑到分数算子的局部性质，大多数的数值方法在每个时间层上去逼近分数阶导数都需要使用前面所有时间层的值。因此，在实际计算中，它们的存储成本会很高。为此，本文使用指数和去近似时间分数阶Caputo导数项可以节约存储成本和计算时间。接下来，我们对SOE算法做一个简要的回顾。

首先，u在 $t_n$ 时刻的SOE逼近如下：

${{}_0{}^{C}D{}_t^{\alpha }u\left(t\right)|}_{t=t_n}=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle {\int }_{t_{n-1}}^{t_n}\frac{u^{\prime }\left(s\right)}{{\left(t_n-s\right)}^{\alpha }}\text{d}s}+\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle {\int }_{t_0}^{t_{n-1}}\frac{u^{\prime }\left(s\right)}{{\left(t_n-s\right)}^{\alpha }}\text{d}s}\triangleq G_1\left(t_n\right)+G_2\left(t_n\right),$

SOE逼近将积分区间分为两项。一项为当前项 $G_1\left(t_n\right)$ ，对于这一项，直接通过线性插值和分部积分得到，即 $G_1\left(t_n\right)\approx \frac{u\left(t_n\right)-u\left(t_{n-1}\right)}{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}$ 。然而，对于历史项 $G_2\left(t_n\right)$ 的计算就比较复杂。先对 $G_2\left(t_n\right)$ 用一次分部积分得到

$G_2\left(t_n\right)=\frac{1}{\Gamma \left(1-\alpha \right)}\left[\frac{u\left(t_{n-1}\right)}{{\tau }^{\alpha }}-\frac{u\left(t_0\right)}{t_n^{\alpha }}-\alpha {\displaystyle {\int }_0^{t_{n-1}}\frac{u\left(s\right)}{{\left(t_n-s\right)}^{1+\alpha }}\text{d}s}\right],$

在用SOE逼近处理上述式子中的积分项之前，先假设SOE逼近的节点为 $s_i$ ，逼近的权重系数为 $w_i$ 以及逼近的项数为K，然后可以得到如下的一个逼近公式：

$G_2\left(t_n\right)\approx \frac{1}{\Gamma \left(1-\alpha \right)}\left[\frac{u\left(t_{n-1}\right)}{{\tau }^{\alpha }}-\frac{u\left(t_0\right)}{t_n^{\alpha }}-\alpha {\displaystyle \underset{i=1}{\overset{K}{\sum }}{w}_i}{H}_i\left(t_n\right)\right],$

其中 $H_i\left(t_n\right)={\displaystyle {\int }_0^{t_{n-1}}{\text{e}}^{-\left(t_n-s\right)s_i}u\left(s\right)\text{d}s}$ 。注意到 $H_i\left(t_n\right)$ 有下面一个递归公式：

$H_i\left(t_n\right)={\text{e}}^{-s_i\tau }{H}_i\left(t_{n-1}\right)+{\displaystyle {\int }_{t_{n-2}}^{t_{n-1}}{\text{e}}^{-\left(t_n-s\right)s_i}}u\left(s\right)\text{d}s,$

对上述递归公式的积分项再做一次线性插值，就可得到如下的逼近公式：

${\displaystyle {\int }_{t_{n-2}}^{t_{n-1}}{\text{e}}^{-s_i\left(t_n-t\right)}}u\left(t\right)\text{d}t\approx \frac{{\text{e}}^{-s_i\tau }}{s_i^2\tau }[\left({\text{e}}^{-s_i\tau }-1+s_i\tau \right)u\left(t_{n-1}\right)+\left(1-{\text{e}}^{-s_i\tau }-{\text{e}}^{-s_i\tau }{s}_i\tau \right)u\left(t_{n-2}\right)],$ (3.1)

为了简化表达，我们记 $u\left(t_n\right)=u^n,1\le n\le N$ 。

因此，综合上面的讨论，我们最终得到了Caputo时间导数项(2.2)的快速近似如下：

${}_0{}^{C}D{}_t^{\alpha }{u}^n\approx \frac{u^n-u^{n-1}}{{\tau }^{\alpha }\Gamma \left(2-\alpha \right)}+\frac{1}{\Gamma \left(1-\alpha \right)}\left[\frac{u^{n-1}}{{\tau }^{\alpha }}-\frac{u^0}{t_n^{\alpha }}-\alpha {\displaystyle \underset{i=1}{\overset{K}{\sum }}{\omega }_i}{H}_i\left(t_n\right)\right]\triangleq {}_0{}^{SOE}D{}_t^{\alpha }{u}^n,\text{for}n\ge 2,$ (3.2)

当 $n=1$ 时，有 $H_i\left(t_n\right)=0$ ，因此可以得到

${}_0{}^{SOE}D{}_t^{\alpha }{u}^1=\frac{{\tau }^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left(u^1-u^0\right).$ (3.3)

基于第二节中对空间方向上的WENO近似和以上对时间Caputo导数的SOE近似，我们将时间和空间方向上的离散格式结合得到方程(2.1)的全离散格式。首先，我们将空间区域 $\left[x_l,x_r\right]$ 均匀划分为M份，将时间区间 $(0,T]$ 均匀划分为N份。并且设 $x_j=x_l+jh\left(0\le j\le M\right)$ ， $t_k=k\tau \left(0\le k\le N\right)$ ，空间步长和时间步长分别为 $\Delta x=\frac{x_r-x_l}{M}$ ， $\tau =\frac{T}{N}$ 。

当微分算子L是梯度算子，WENO-SOE格式求解方程(2.1)的全离散格式如下：

${}_0{}^{SOE}D{}_t^{\alpha }{u}_j^k=\frac{{\hat{f}}_{j+1/2}^k-{\hat{f}}_{j-1/2}^k}{\Delta x}+h_j^{k-1}+f_j^k,0\le j\le M,1\le k\le N.$

当微分算子L是拉普拉斯算子，WENO-SOE格式求解方程(2.1)的全离散格式则为：

${}_0{}^{SOE}D{}_t^{\alpha }{u}_j^k=\frac{{\hat{g}}_{j+1/2}^k-{\hat{g}}_{j-1/2}^k}{\Delta x^2}+h_j^{k-1}+f_j^k,0\le j\le M,1\le k\le N.$

4. 数值实验

在本节中，将通过数值实验来验证所提方法的高阶精度以及应用WENO格式求解含间断解方程的本质无振荡性质。记 $E_2$ 和 $E_{\infty }$ 分别为 $L_2$ 范数和无穷范数下精确解和数值解之间的误差，定义如下：

$E_2=\sqrt{h{\displaystyle \underset{j=0}{\overset{M}{\sum }}{\left(u_j-{\tilde{u}}_j\right)}^2}},E_{\infty }=\underset{0\le j\le M}{\max }\left|u_j-{\tilde{u}}_j\right|,$

其中 $u_j$ 和 ${\tilde{u}}_j$ 分别表示精确解和数值解。

例1 考虑以下的时间分数阶Fisher方程：

$\{\begin{array}{l}{D}_t^{\alpha }u\left(x,t\right)-\Delta u\left(x,t\right)-\lambda u\left(x,t\right)\left(1-u^{\gamma }\left(x,t\right)\right)=f\left(x,t\right),\left(x,t\right)\in \left(-2\pi ,2\pi \right)\times \left(0,1\right],\\ u\left(x,0\right)=0,x\in \left[-2\pi ,2\pi \right],\\ u\left(-2\pi ,t\right)=u\left(2\pi ,t\right)=0,t\in \left(0,1\right],\end{array}$

其中 $\lambda =-1,\gamma =1$ ， $f\left(x,t\right)=\left(\frac{2t^{\left(2-a\right)}}{\Gamma \left(3-a\right)}+2t^2-t^4\sin \left(x\right)\right)\sin \left(x\right)$ 。上述方程的精确解的表达式是 $u\left(x,t\right)=t^2\sin \left(x\right)$ 。

Table 1. Numerical result of solving Example 1 in WENO format combined with SOE method ( α take 0.5)

表1. 用WENO格式结合SOE方法求解例1的数值结果( $\alpha$ 取0.5)

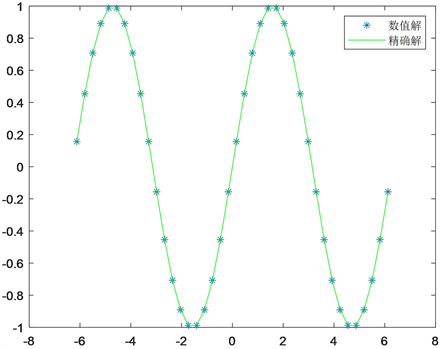
Figure 1. Numerical and exact solutions of $u\left(x,t\right)$ in Example 1

图1. 例1中 $u\left(x,t\right)$ 的数值解与精确解

从表1中可以看出，应用WENO格式离散空间方向上的两阶导数数值求解例1可以达到空间高精度。其次从图1中可以看出 $u\left(x,t\right)$ 的数值解与精确解的曲线一致，这也反映了所提WENO-SOE格式的有效性。

例2 考虑以下的时间分数阶Burgers方程：

$\{\begin{array}{l}{\partial }_t^{\alpha }u\left(x,t\right)+u\left(x,t\right){\partial }_{x}u\left(x,t\right)=0,\left(x,t\right)\in \left(-1,1\right)\times \left(0,0.5\right],\\ u\left(x,0\right)=-\sin \left(\pi x\right),x\in \left[-1,1\right],\\ u\left(-1,t\right)=u\left(1,t\right)=0,t\in \left(0,0.5\right],\end{array}$

Figure 2. The numerical solution of $u\left(x,t\right)$ in Example 2

图2. 例2中 $u\left(x,t\right)$ 的数值解

例2考虑的是带连续初值的Burgers方程，它在经过一定时间T后精确解会发生间断，利用WENO的本质无振荡性质可以有效的抑制解的振荡，图2的数值结果印证了这一性质。

5. 结论

本文采用加权本质无振荡(WENO)有限差分格式来近似空间方向上的导数，且采用指数和近似(SOE)方法来近似时间Caputo导数，该WENO-SOE格式在光滑区域具有很高的精度，并保持了间断处的本质无振荡性质。最后通过数值实验，验证了该格式的数值高精度和有效性。

基金项目

本项目由2022年江西省研究生创新专项资金项目(YC2022-s738)资助。