序决策系统下基于图顶点最小覆盖的属性约简

Attribute Reduction Based on Minimum Cover of Graph Vertices in Ordered Decision System

摘要: 现如今的互联网时代，数据维度灾难性增长，如何从高维数据中提取有用信息成为一大难题。属性约简是数据预处理的重要步骤之一，能够减少属性维度和计算复杂度，提高分类性能和可解释性。传统的属性约简方法主要基于信息论、统计学或启发式算法，存在不足之处。本文提出了一种基于图顶点最小覆盖的序决策系统属性约简方法，利用图来建模属性之间的依赖关系，使属性约简算法和图论知识相结合。实验结果表明，本文方法在多个数据集上具有较好的约简效果和分类性能，具有良好的可解释性和可视化效果。

Abstract: In today’s Internet era, the data dimension has grown more dramatically, and how to extract useful information from high-dimensional data has become a big problem. Attribute reduction is one of the important steps of data preprocessing, which can reduce the attribute dimension and computa-tional complexity, and improve the classification performance and interpretability. Traditional at-tribute reduction methods are mainly based on information theory, statistics or heuristic algorithms, which are shortcomings. In this paper, we propose a method based on the minimum cover-age of graph vertices to model the dependencies between properties and combining the attribute reduction algorithm and graph theory knowledge. Experimental results show that the present method has good reduction and classification performance on multiple datasets, with good inter-pretability and visualization.

1. 引言

基于集合论，波兰学者Pawlak于1982年提出了粗糙集理论 [1] ，粗糙集理论是用于处理不精确、不一致、不完备信息和知识的有效工具，其主要思想是通过上下近似来表示数据中的确定性与不确定性，从而推导出相应的决策规则。属性约简 [2] [3] [4] [5] 作为粗糙集理论数据预处理中的一个重要步骤，目的是减少属性维度和计算复杂度，做到数据降维。目前，许多学者对属性约简作了深入的研究并取得了很多成果 [6] [7] [8] [9] [10] ，但目前的研究大多以在传统粗糙集理论不断改进启发式属性约简或差别矩阵算法为主 [11] [12] [13] 。

超图是图论中的一种扩展，能够表示节点之间的多重关系，被广泛应用于数据分析、图像分割、社交网络等领域。超图应用于数据分析主要包括超图聚类、超图分析、超图可视化等方面。超图理论将数据点作为节点，利用超图表达样本之间的关系。超图分析方法将数据点和特征作为节点，利用超图表达数据之间的依赖关系，实现数据分析，能够将复杂数据映射到超图上，展示数据之间的关系和特征，提高数据的可视化效果和理解性。

本文从超图理论的角度出发，将超图理论的最小顶点覆盖算法与序决策系统相结合，提高约简效率。经实验证明本文所提算法具备一定的有效性。

2. 基本概念

2.1. 序决策系统

设一个四元组 $CIS=\left(U,AT,V,f\right)$ 为一个信息系统，如果在信息系统CIS中的某一属性的值域上存在偏序关系，则称该属性为一个准则。当CIS中每个属性都为一个准则时，该系统为一个序决策系统 $OIS=\left(U,AT,V,f\right)$ 。其中：

· U：表示所有对象的集合，称为论域。

· AT：包含条件属性集合C和决策属性集合D。

· V：表示条件属性集合C和决策属性集合D的值域。

· f：代表一个映射函数 $f:U\times AT\to V$ ，论域中的每一个对象在条件属性和决策属性上对应一个属性值，即 $f\left(x_i,c_k\right)=c_k\left(x_i\right)$ 。

定义1 [14] 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中，对于 $\forall \mathbb{Q}\subseteq C$ ，有优势关系定义如下：

$Dominance\left(\mathbb{Q}\right)=\left\{\left(x_i,x_j\right)\in U\times U|\forall q\in \mathbb{Q},f\left(x_i,q\right)\ge f\left(x_j,q\right)\right\}$ (1)

且满足 $Dominance\left(\mathbb{Q}\right)={\cap }_{c\in B}Dominance\left(\left\{c\right\}\right)$ 。其中， $f\left(x_i,q\right)\ge f\left(x_j,q\right)$ 表示在属性q下，对象 $x_i$ 优于对象 $x_j$ 。

优势关系是一个满足自反性、传递性和不对称性的偏序关系。因此，优势关系 $Dominance\left(\mathbb{Q}\right)$ 可以导出论域在条件属性子集上的覆盖 $U/Dominance\left(\mathbb{Q}\right)=U/\mathbb{Q}=\left\{{\left[x_i\right]}_{\mathbb{Q}}^{\ge }|x_i\in U\right\}$ 。其中， ${\left[x_i\right]}_{\mathbb{Q}}^2$ 称之为优势类，且 ${\left[x_i\right]}_{\mathbb{Q}}^{\ge }=\left\{x_j\in U|\left(x_j,x_i\right)\in Dominance\left(\mathbb{Q}\right)\right\}$ 。在决策属性上，同样有一个覆盖表示为 $U/D=\left\{{\left[x_i\right]}_D^{\ge }|x_i\in U\right\}=\left\{D_1^{\ge },D_2^{\ge },\cdots ,D_n^{\ge }\right\}$ ，其中 ${\left[x_i\right]}_D^{\ge }=\left\{x_j\in U|\left(x_j,x_i\right)\in Dominance\left(D\right)\right\}$ 称之为决策类。

定义2 [14] 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中，对于 $\forall \mathbb{Q}\subseteq C$ ，有下、上近似定义如下：

${\underset{\_}{Dominance}}_{\mathbb{Q}}\left(D_i^{\ge }\right)=\left\{x_i\in U|{\left[x_i\right]}_{\mathbb{Q}}^{\ge }\subseteq D_i^{\ge }\right\}$ (2)

${\overline{Dominance}}_{\mathbb{Q}}\left(D_i^{\ge }\right)={\cup }_{x_i\in D_i^{\ge }}{\left[x_i\right]}_{\mathbb{Q}}^{\ge }$ (3)

且边界域表示为 $BN{D}_{\mathbb{Q}}\left(D_i^{\ge }\right)={\overline{Dominance}}_{\mathbb{Q}}\left(D_i^{\ge }\right)-{\underset{\_}{Dominance}}_{\mathbb{Q}}\left(D_i^{\ge }\right)$ 。

2.2. 超图

超图理论是对传统图论的扩展和推广。在传统图论中，图由节点和边组成，而超图引入了超边的概念，以允许节点之间的多重关系。在超图中，超边可以连接多个节点，而传统图中的边只能连接两个节点。超边可以连接任意数量的节点，从而更好地捕捉节点之间的复杂关系。每个节点和超边可以具有任意类型的属性，这使得超图可以应用于各种实际问题。

定义3 [15] 设超图为一个二元组 $H=\left(V,E\right)$ ，其中 $V=\left\{v_1,v_2,\cdot \cdot \cdot ,v_n\right\}$ 为顶点集合， $E=\left\{e_1,e_2,\cdots ,e_m\right\}$ 为超边集合。

如图1所示为一个超图，共包含13个顶点和8条超边。

Figure 1. The hypergraph example

图1. 超图示例

3. 基于序决策系统的下近似属性约简算法

序决策系统的下近似约简定义如下：

定义4 [14] 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中，对于 $\forall \mathbb{Q}\subseteq C$ ， $U/D=\left\{D_1^{\ge },D_2^{\ge },\cdots ,D_n^{\ge }\right\}$ 。当 $RED\subseteq C$ 为序决策系统的下近似约简，当且仅当满足以下条件：

1) 对于 $\forall D_i^{\ge }\in U/D$ ，有 ${\underset{\_}{Dominance}}_{RED}\left(D_i^{\ge }\right)={\underset{\_}{Dominance}}_C\left(D_i^{\ge }\right)$ ；

2) 对于 $\forall red\in RED$ ， $\exists D_i^{\ge }\in U/D$ ，有 ${\underset{\_}{Dominance}}_{red}\left(D_i^{\ge }\right)\ne {\underset{\_}{Dominance}}_{RED}\left(D_i^{\ge }\right)$ 。

条件(1)为联合充分性，条件(2)为个体必要性。

定义5 [14] 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中，对于 $\forall \mathbb{Q}\subseteq C$ ， $U/D=\left\{D_1^{\ge },D_2^{\ge },\cdots ,D_n^{\ge }\right\}$ 。 $Matri{x}_{OIS}=\left(M_{OIS}\left(x_i,x_j\right)\right)$ 为一个规模为 ${\left|U\right|}^2$ 的差别矩阵。且满足以下条件：

$M_{OIS}\left(x_i,x_j\right)=\{\begin{array}{ll}\left\{c_k:c_k\in C\right\},\hfill & \left(x_i,x_j\right)\in Condition\hfill \\ \varnothing ,\hfill & \text{otherwise}\hfill \end{array}$ (4)

其中， $Condition={\cup }_{D_i^{\ge }\in U/D}\left\{\left(x_i,x_j\right)|x_i\notin Dominanc{e}_C\left(D_i^{\ge }\right),x_j\in Dominanc{e}_C\left(D_i^{\ge }\right)\right\}$ 。

定义6 [14] 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中，对于 $\forall \mathbb{Q}\subseteq C$ ， $U/D=\left\{D_1^{\ge },D_2^{\ge },\cdots ,D_n^{\ge }\right\}$ 。 $Matri{x}_{OIS}=\left(M_{OIS}\left(x_i,x_j\right)\right)$ 为一个规模为 ${\left|U\right|}^2$ 的差别矩阵，其差别函数定义如下：

$F_{OIS}\left(x_i,x_j\right)=\wedge \left(\vee M_{OIS}\left(x_i,x_j\right)\right)$ (5)

基于上述定义，给出序决策系统下经典差别矩阵算法(Classical discernibility matrix algorithm in ordered decision system, CDM-ODS) (表1)。

Table 1. Classical discernibility matrix algorithm in ordered decision system (CDM-ODS)

表1. 序决策系统下经典差别矩阵算法

4. 基于图顶点最小覆盖的属性约简算法

差别矩阵算法进行属性约简的过程与图论中寻找最小顶点覆盖集之间存在共同点。因此针对这种情况，可以将序决策系统构造出的差别矩阵生成一张超图，在超图上进行求解顶点最小覆盖。

定义7 设二元组 $H=\left(V,E\right)$ 为一个超图，V顶点集合，E是超边集合。在超图 $H=\left(V,E\right)$ 中定义如下布尔函数：

$F_H=\wedge \left\{\vee e:e\in E\right\}$ (6)

对该函数求解极小析取范式所得结果就是最小顶点覆盖集合。

定义8 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中， $Matri{x}_{OIS}=\left(M_{OIS}\left(x_i,x_j\right)\right)$ 为序决策系统生成的差别矩阵，由该系统差别矩阵导出的超图定义如下：

$H_{OIS}=\left(V,E\right)$ (7)

其中，顶点集合 $V=C$ ，超边集合 $E=M_{OIS}\left(x_i,x_j\right)$ 。

定义9 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中， $Matri{x}_{OIS}=\left(M_{OIS}\left(x_i,x_j\right)\right)$ 为序决策系统生成的差别矩阵，由该系统差别矩阵导出的超图为 $H_{OIS}=\left(V,E\right)$ 。顶点集合 $V=C$ ，则V中顶点的度表示为 $Degre{e}_H\left(v_i\right)$ ，顶点的度表示为与顶点相关联的超边数。

定理1 在序决策系统 $OIS=\left(U,AT,V,f\right)$ 中， $H_{OIS}=\left(V,E\right)$ 为序决策系统的差别矩阵生成的超图，则有 $RE{D}_{OIS}=Vertex\left(H_{OIS}\right)$ 。

其中， $Vertex\left(H_{OIS}\right)$ 代表超图 $H_{OIS}=\left(V,E\right)$ 的定点最小覆盖。

证明：

要证明 $RE{D}_{OIS}=Vertex\left(H_{OIS}\right)$ 首先假设 $Matri{x}_{OIS}=\left(M_{OIS}\left(x_i,x_j\right)\right)$ 为该系统生成的差别矩阵。通过定义8可知诱导超图 $H_{OIS}=\left(V,E\right)$ 的超边集合 $E=M_{OIS}\left(x_i,x_j\right)\in Matri{x}_{OIS}$ ，因此有 $E\subseteq Matri{x}_{OIS}$ 。这将分为以下两种情况：

情况一： $E=Matri{x}_{OIS}$ ；

情况二： $E\subset Matri{x}_{OIS}$ 。

在情况一中，通过定义7可知显然 $F_H=\wedge \left\{\vee e:e\in E\right\}=F_{OIS}\left(x_i,x_j\right)=\wedge \left(\vee M_{OIS}\left(x_i,x_j\right)\right)$ ；在情况二中，由 $E\subseteq Matri{x}_{OIS}$ 可知 $Matri{x}_{OIS}=E\cup \left\{C\right\}$ ，即 $M_{OIS}\left(x_i,x_j\right)\in Matri{x}_{OIS}\subset C$ ，根据吸收律可得 $\left(\vee M_{OIS}\left(x_i,x_j\right)\right)\wedge \left(\vee C\right)=\vee M_{OIS}\left(x_i,x_j\right)$ 。综上得 $F_H=\wedge \left\{\vee e:e\in E\right\}=F_{OIS}\left(x_i,x_j\right)=\wedge \left(\vee M_{OIS}\left(x_i,x_j\right)\right)$ 。

基于上述定理，给出序决策系统下基于图顶点最小覆盖的属性约简算法(Attribute reduction algorithm based on graph vertex minimum cover in ordered decision system, ARGVMC-ODS) (表2)。

Table 2. Attribute reduction algorithm based on graph vertex minimum cover in ordered decision system, ARGVMC-ODS

表2. 序决策系统下基于图顶点最小覆盖的属性约简算法

5. 实验分析

本实验选取八组UCI数据集进行约简效率和分类精度的对比，详细信息如表3所示。在验证算法有效性之前，使用WEKA3.8对数据集进行离散化预处理。本节进行的所有的实验都是在一台带有MacOS13.0 Ventura、Intel(R) Core(TM) i9-9880H八核2.30 GHz CPU和16GB内存的笔记本电脑上进行。算法在Pycharm2023开发工具是使用Python编写，实验图使用MatlabR2021a绘制。

Table 3. Data set information

表3. 实验使用的数据集

5.1. 约简效率

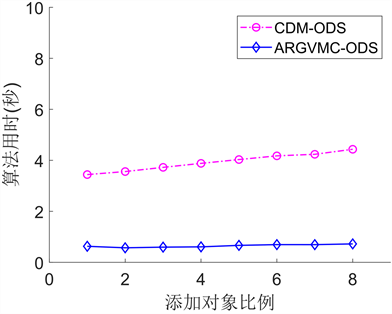
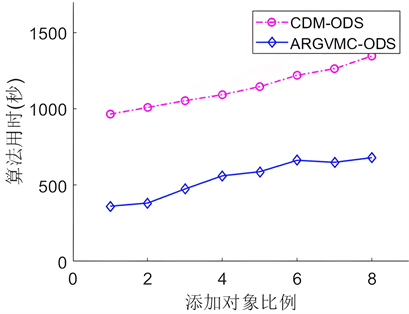
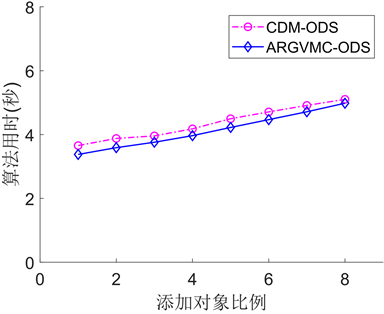
如图2所示为本文所提算法ARGVMC-ODS与经典差别矩阵算法CDM-ODS在序决策系统下按论域规模比例均匀增加时的算法执行时间曲线。从中可以看出，当论域中的对象数量比例较小时，算法效率差别不大。当对象的规模逐渐增大时，两种算法的执行时间均有上升，并且经典差别矩阵算法CDM-ODS

(a) Wine (b) Abalone (c) Car

(d) Breast Cancer (e) Concrete (f) Connectionist Bench(g) Yeast (h) Zoo

Figure 2. Comparison of reduction efficiency

图2. 约简效率对比

的执行时间始终最长。本文所提算法ARGVMC-ODS与之相比，整体运行时间都有所缩短，且变化较均匀。因此，本文所提算法ARGVMC-ODS相对于经典差别矩阵算法CDM-ODS的约简效率较高，在大规模数据集上优势较为明显。

5.2. 分类精度

如图3与图4所示为本文所提算法ARGVMC-ODS与经典差别矩阵算法CDM-ODS在序决策系统下在不同数据集上分别在KNN与SVM分类器上的分类精度对比。在本实验中采取十倍交叉验证的方法计算分类精度。其中，经典差别矩阵算法CDM-ODS能够得出所有约简结果，而本文所提算法ARGVMC-ODS能够得出最短结果，因此对经典差别矩阵算法CDM-ODS的约简结果取平均值。从图中可以看出，本文所提算法在实验数据集上有较高的分类精度。

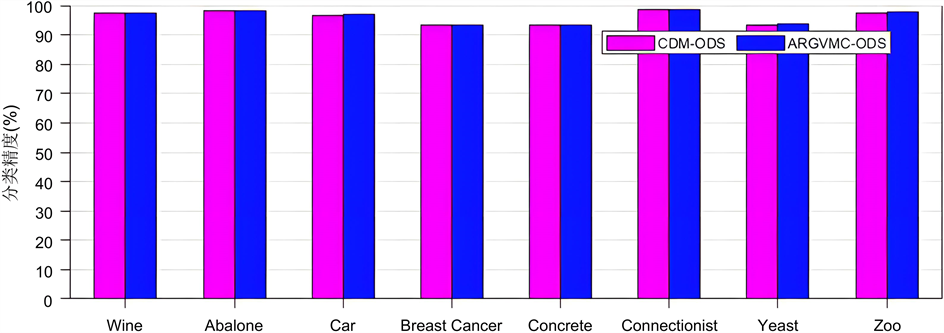
Figure 3. Comparison of classification accuracy (KNN)

图3. 分类精度对比(KNN)

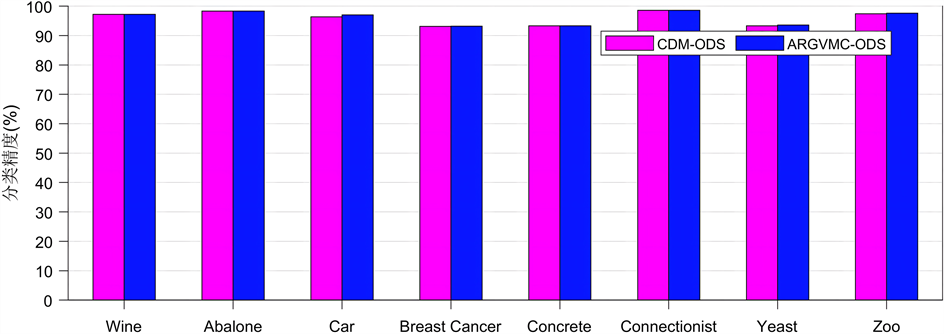
Figure 4. Comparison of classification accuracy (SVM)

图4. 分类精度对比(SVM)

6. 结论

在本文中，首先通过寻找最小顶点覆盖和差别矩阵属性约简的共性，进一步提出在序决策系统回顾下基于顶点最小覆盖的属性约简算法，将图论与粗糙集理论相融合。本文所提算法ARGVMC-ODS与差别矩阵算法思想相比，无需计算最小析取范式，避免了时间复杂度过高的问题，能够提高算法效率。通过选取的八组UCI数据集上进行算法有效性验证。从实验结果可以看出，本文所提算法相比于传统的差别矩阵算法效率较高。

基金项目

本文受烟台市科技计划项目(编号：2022XDRH016)的资助。