具有预测沥青混合料刚度参数的多尺度算法

doi:10.12677/AAM.2023.1210430

期刊菜单

具有预测沥青混合料刚度参数的多尺度算法
Multi-Scale Algorithm with Predicted Stiffness Parameters of Asphalt Mixture

DOI: 10.12677/AAM.2023.1210430, PDF, HTML, XML, 下载: 180 浏览: 218 国家自然科学基金支持
作者: 彭姝婉, 李佩洪：长沙理工大学数学与统计学院，湖南长沙
关键词: 沥青混合料；刚度参数；双尺度算法；多尺度算法；细观结构；Asphalt Mixture； Stiffness Parameters； Two-Scale Algorithm； Multi-Scale Algorithm； Thin Structure

摘要: 为了验证多尺度算法对沥青混合料的弹性力学刚度参数的有效性问题，本文分析了多尺度算法及沥青混合料细观模型特性，提出了多尺度算法运用于随机复合材料的理论方法及表征。统计含不同粒径集料沥青混合料细观骨料分布特性，依据骨料分布特性规律在尺度区域内随机生成细观骨料，选取各类沥青混合料计算尺度区域，依据骨料随机分布特性在尺度区域内生成细观尺度模型。运用多尺度算法预测沥青混合料疲劳过程刚度参数，提出了计算沥青混合料疲劳损伤过程刚度参数的多尺度算法流程。结论是多尺度算法用于沥青混合料的刚度参数是有效的，该算法可以为类似的实际工程提供一定的参考意义。

Abstract: In order to verify the effectiveness of multi-scale algorithm on the elastic stiffness parameters of asphalt mixture, this paper analyzes the characteristics of multi-scale algorithm and the fine model of asphalt mixture, and proposes the theoretical method and characterization of multi-scale algo-rithm for random composite materials. The distribution characteristics of fine aggregate of asphalt mixture with different particle sizes are counted, the fine aggregate is randomly generated in the scale area according to the distribution characteristics of aggregate, and the scale area of various kinds of asphalt mixture is selected to calculate the scale, and the fine scale model is generated in the scale area according to the random distribution characteristics of aggregate. A multi-scale algo-rithm is used to predict the stiffness parameters of the fatigue process of asphalt mixture. The con-clusion is that the multi-scale algorithm is effective for the stiffness parameter of asphalt mixture, and this algorithm can provide some reference significance for similar practical engineering.

文章引用：彭姝婉, 李佩洪. 具有预测沥青混合料刚度参数的多尺度算法[J]. 应用数学进展, 2023, 12(10): 4365-4377. https://doi.org/10.12677/AAM.2023.1210430

1. 引言

沥青作为一种复合材料，近年来普遍应用于道路工程中，沥青路面优越的使用性能提高了道路运输效率并且带来良好经济效益。但是在使用过程中沥青路面病害亦随之发生，车辆重复荷载作用使沥青混合料内部出现损伤导致材料使用性能降低，影响了道路使用效率，这些问题引起众多专家学者和技术人员高度重视。因此运用多尺度算法预测疲劳损伤过程沥青混合料弹性力学刚度参数，从而丰富沥青混合料疲劳损伤过程力学参数研究成果。

多尺度算法近年来已经在岩土、航空等多个领域得到广泛应用，在解决粘弹性复合材料损伤行为方面取得了很好的效果。多尺度分析方法的主要优点是：在解决细观力学问题时可以见到小尺度物理现象，可以进一步了解局部细观尺度的材料特性。另一个优点是：一旦确定了材料组成成分的单个材料性能，则材料组成成分分布和每个体积单元及由此产生的合成材料有效性就可以通过计算来确定，从而不必进行大量的室内试验。借助多尺度算法理论编制程序预测沥青混合料刚度参数的研究是本文的创新点，因此本文着重于以多尺度算法预测沥青混合料疲劳损伤过程的刚度参数特性，这对于丰富沥青混合料在使用过程中材料性能参数的研究成果具有重要意义。

随着计算机技术和材料学科进步，材料性能预测及仿真力学模拟技术不断出现，学术界已有学者运用多尺度方法对非均质材料进行研究，另外还有学者通过研究复合材料力学问题提出基于尺度计算模型或仿真计算方法 [1] - [13] 。总结已有研究经验，本文运用多尺度算法预测随机复合材料沥青混合料弹性力学性能(弹性模量E及泊松比μ)。首先通过CT扫描技术获取AC-13C及含各不同粒径集料沥青混合料细观图像，统计不同粒径骨料随机分布并随机生成骨料分布状态；第二根据统计的随机骨料分布状态在Abaqus有限元软件内建立符合各类沥青混合料骨料特性的二维细观模型；然后对不同粒径集料及基体材料赋予参数；接着运用多尺度算法理论通过算法程序计算各种尺度区域的沥青混合料模型；最后得出沥青混合料均匀化后的刚度参数E、μ并分析刚度参数变化规律。本文主要针对沥青混合料骨料随机分布统计、沥青混合料细观模型建立及多尺度算法流程进行研究。

2. 具有预测随机复合材料力学参数的多尺度算法

在细观状态下研究沥青混合料疲劳损伤刚度特性，通过设计含不同粒径集料沥青混合料以劈裂回弹模量测试方法测定疲劳损伤过程沥青混合料的刚度参数。同时运用多尺度算法把离散的材料模型通过数学均匀化函数将不同类型材料均匀化成为一个整体刚度参数。细观状态沥青混合料是由多种不同级配集料和沥青胶结料组成，二者材料属性不同；同时集料粒径大小差异较大，为准确计算细观状态沥青混合料刚度参数，需要建立含小粒径尺寸集料的尺度模型到完全能包括所有粒径集料的尺度模型，逐步均匀化含不同粒径集料沥青混合料模型样本预测疲劳过程各类沥青混合料的刚度参数结果。

为预测随机复合材料的力学参数，本文提出一种多尺度计算方法，基于数学推导形式提出了双尺度表示方法和基于双尺度分析的多尺度计算方法用于预测多种级配颗粒复合材料的力学参数。

2.1. 随机分布复合材料力学参数的双尺度表示

利用双尺度方法求解沥青混合料的等效弹性力学参数时，本文做出三个假设：

1) 如果等效力学参数 ${\hat{a}}_{i j h k} (ω)$ 是一个有界随机变量，它的期望值 $E {\hat{a}}_{i j h k} (ω)$ 存在。

2) $a^{ε}_{i j h k} (ω) \in C^{1} (Ω)$ ，并且 $f (x) = C^{\infty} (Ω)$ 如果仅仅是 $a^{ε}_{i j h k} (x, ω) \in L^{2} (Ω)$ ，可以构造一个光滑算子 $δ : a^{ε}_{i j h k} (x, ω) \to δ a^{ε}_{i j h k} (x, ω) \in C^{1} (Ω)$ 满足 $‖ δ a^{ε}_{i j h k} (\cdot, ω) - a^{ε}_{i j h k} (\cdot, ω) ‖ \to 0$ 当 $δ \to 0$ 。

3) ${({\hat{a}}^{ε}_{i j h k} (x, ω))}_{n \times n}$ 是对称和正定矩阵，存在两个正数不依赖 $ω$ 的正数 $c_{1}$ 和 $c_{2}$ 满足 $c_{1} η_{i h} η_{i h} \leq a^{ε}_{i j h k} (x, ω) η_{i j} η_{h k} \leq c_{2} η_{i h} η_{i h} \forall x \in Ω$ ； $Ω$ 表示同一尺度颗粒分布的统计区域如图3.25；其中 ${η_{i h}}$ 是对称矩阵。同时假定区域 $Ω$ 同上，是具有同尺度颗粒随机分布的沥青混合料区域 $Ω$ ，即 $Ω = U_{(ω^{s}, t \in Z)} ε (Q^{s} + t)$ 。为了获取具有随机分布骨料沥青混合料的等效力学参数，考虑如下弹性问题。

${\begin{cases} \frac{\partial}{\partial x_{j}} [a^{ε}_{i j h k} (x, ε) \frac{1}{2} (\frac{\partial u_{h}^{ε} (x, ε)}{\partial x_{k}} + \frac{\partial u_{k}^{ε} (x, ε)}{\partial x_{h}})] = f_{i} (x) x \in Ω \\ u^{ε} (x, ω) = \bar{u} (x) x \in \partial Ω \end{cases}$ (1.1)

其中 $i, j, h, k = 1, 2, \dots, n$ 。由Korn’s不等式和Lax-Milgram定理，方程式1.1有一个唯一解 $u^{ε} (x, ω)$ 。

对于具有颗粒随机分布的沥青混合料，工程师常采用等效力学参数 ${\hat{a}}_{i j h k}$ 去分析复合材料的力学行为。在后文中将用构造的方法在每一个单胞 $ε Q^{s}$ ( $ε Q^{s}$ 表示同样尺度颗粒的统计窗，建立双尺度公式去计算等效力学参数 ${\hat{a}}_{i j h k}$ (期望均匀化系数)。

先假设此处存在一组力学参数 ${{\hat{a}}_{i j h k}}$ 在整个沥青混合料区域Ω中满足集料粒径条件，而且向量值函数 $u^{0} (x)$ 是如下问题的解。

${\begin{cases} {\hat{a}}_{i j h k} \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{k}}) = f_{i} (x) x = Ω \\ u^{0} (x, ω) = \bar{u} (x) x = \partial Ω \end{cases}$ (1.2)

此处 $u^{0} (x)$ 将被称为在 $Ω$ 上的期望均匀化解， ${{\hat{a}}_{i j h k}}$ ( $i, j, h, k = 1, \dots, n$ )是 $Ω$ 内的期望均匀化系数。基于Korn’s不等式和Lax-Milgram定理，通过假设(2)，存在一个唯一解 $u^{0} (x)$ 。如果区域 $Ω$ 属于 $C^{2, β} (Ω)$ ( $β > 0$ )并且边界是分片光滑和 $f_{i} (x) = C^{2, β} (Ω)$ ( $i = 1, \dots, n$ )，则向量值函数 $u^{0} (x) \in H^{4} (Ω)$ 。

由假设(3)，根据Korn’s不等式和Lax-Milgram定理，对每一个确定的结构 $Ω$ 。方程式3.5有唯一解 $u^{ε} (x, ω)$ 。从弹性方程式1.1可知，位移 $u^{ε} (x, ω)$ 和应力依赖于整体结构 $Ω$ 和在每一个单胞体 $ε Q^{s}$ 的微观分布，所以位移可以表示为 $u^{ε} (x, ω) = u^{ε} (x, ξ, ω)$ ，x表示整体结构的性能和行为， $ξ$ 表示 $Q^{s}$ 中的局部坐标以及随机骨料的影响。为获取随机颗粒分布沥青混合料力学性能参数的双尺度格式，假定 $u^{ε} (x, ω)$ 有如下展式。

$u^{ε} (x, ω) = u^{0} (x) + ε N_{α 1} (ξ, ω^{s}) \frac{\partial u^{0} (x)}{\partial_{x_{α 1}}} + ε^{2} N_{α 1 α 2} (ξ, ω^{s}) \frac{\partial^{2} u (x)}{\partial^{2}_{x_{α 1} x_{α 2}}} + ε^{3} P_{1} (x, ξ, ω)$ (1.3)

其中 $x \in Ω$ ， $ξ = Q^{s}$ ， $ξ = \frac{x}{ε} - [\frac{x}{ε}] \in Q^{s}$ ；此处 $N_{α 1} (ξ, ω^{s})$ 和 $N_{α 1 α 2} (ξ, ω^{s})$ 是函数矩阵，分别表示下式。

$N_{α 1} (ξ, ω^{s}) = (\begin{matrix} N_{α_{1} 11} (ξ, ω^{s}) & \dots & N_{α_{1} 1 n} (ξ, ω^{s}) \\ ⋮ & ⋱ & ⋮ \\ N_{α_{1} n 1} (ξ, ω^{s}) & \dots & N_{α_{1} n n} (ξ, ω^{s}) \end{matrix})$ 及 $N_{α 1 α 2} (ξ, ω^{s}) = (\begin{matrix} N_{α_{1} α_{2} 11} (ξ, ω^{s}) & \dots & N_{α_{1} α_{2} 1 n} (ξ, ω^{s}) \\ ⋮ & ⋱ & ⋮ \\ N_{α_{1} α_{2} n 1} (ξ, ω^{s}) & \dots & N_{α_{1} α_{2} n n} (ξ, ω^{s}) \end{matrix})$ (1.4)

从式1.4可得下式。

$u_{h}^{ε} (x, ω) = u_{h}^{0} (x) + ε N_{α_{1} k m} (ξ, ω^{s}) \frac{\partial u_{m}^{0} (x)}{\partial_{x_{α 1}}} + ε^{2} N_{α 1, α 2} (ξ, ω^{s}) \frac{\partial^{2} u_{m}^{0} (x)}{\partial_{x_{α 1} x_{α 2}}^{2}} + ε^{3} P_{1 h} (x, ξ, ω)$ (1.5)

其中 $h, α_{1}, α_{2}, m = 1, 2, \dots, n$ 。

由于 $ξ = \frac{x}{ε}$ ，考虑到下式。

$\frac{\partial u_{i}^{ε} (x, ω^{s})}{\partial x_{j}} = \frac{\partial u_{i} (x, ξ, ω^{s})}{\partial x_{j}} + \frac{1}{ε} \frac{\partial u_{i} (x, ξ, ω^{s})}{\partial ξ_{j}}$ (1.6)

可得到下式。

$\begin{matrix} a_{i j h k} (ε, ω) \frac{1}{2} (\frac{\partial u_{n}^{ε} (x, ω)}{\partial x_{k}} + \frac{\partial u_{n}^{ε} (x, ω)}{\partial x_{h}}) \\ = a_{i j h k} (ε, ω) \frac{1}{2} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) + a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ε, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ε, ω^{s})}{\partial ξ_{h}}) \frac{\partial u_{m}^{0} (x)}{\partial x_{α 1}} \\ + \frac{1}{2} ε a_{i j h k} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s}) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{k} \partial x_{α_{1}}} + \frac{1}{2} ε a_{i j h k} (ε, ω^{s}) N_{α_{1} k m}^{s} (ε, ω^{s}) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{h} \partial x_{α_{1}}} \\ + ε a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ε, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ε, ω^{s})}{\partial ξ_{h}}) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}} \\ + \frac{1}{2} ε a_{i j h k} (ε, ω^{s}) N_{α_{1} α_{2} k m}^{s} (ε, ω^{s}) \frac{\partial^{3} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}} \partial x_{α_{k}}} \end{matrix}$ (1.7)

其中 $T (x, ξ, ω) = a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial P_{1 h} (x, ξ, ω)}{\partial x_{k}} + \frac{\partial P_{1 k} (x, ξ, ω)}{\partial x_{h}})$

从式1.1和1.7可得下列方程。

$\begin{matrix} \frac{\partial}{\partial x_{j}} [a_{i j h k} (ξ, ω) \frac{1}{2} (\frac{\partial u_{h}^{ε}}{\partial x_{k}} + \frac{\partial u_{k}^{ε}}{\partial x_{h}})] \\ = ε^{- 1} \frac{\partial a_{i j h k} (ξ, ω^{s})}{\partial ξ_{j}} \frac{1}{2} (\frac{\partial u_{h}^{0}}{\partial x_{k}} + \frac{\partial u_{k}^{0}}{\partial x_{h}}) + a_{i j h k} (ξ, ω^{s}) \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{h}^{0}}{\partial x_{k}} + \frac{\partial u_{k}^{0}}{\partial x_{h}}) \\ + ε^{- 1} \frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial x_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial x_{h}})] \frac{\partial u_{m}^{0} (x)}{\partial x_{α_{1}}} \end{matrix}$

(1.8)

其中 $ε^{3} V (x, ξ, ω) = ε^{3} \frac{\partial T (x, ξ, ω)}{\partial x_{j}}$ 。

式1.8对于任意 $ε > 0$ 成立，比较方程两边 $ε_{l} (l = - 1, 0, 1, \dots)$ 的系数，可得以下方程。

$\begin{array}{l} \frac{\partial a_{i j h k} (ξ, ω^{s})}{\partial ξ_{j}} \frac{1}{2} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) \\ + \frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \frac{\partial u_{m}^{0} (x)}{\partial x_{α_{1}}} = 0 \end{array}$ (1.9)

利用 ${a_{i j h k}^{ε}}$ 对称性，由式1.9可得下式。

$\frac{\partial}{\partial ξ_{j}} [a_{i j m α_{1}} (ξ, ω^{s}) + a_{i j m k} (ξ, ω^{s}) + \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \frac{\partial u_{m}^{0} (x)}{\partial x_{α_{1}}} = 0$ (1.10)

对于沥青混合料复合材料在每个单胞上相互独立有下列方程。

$\frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}})] = - \frac{\partial a_{i j m α_{1}} (ξ, ω^{s})}{\partial ξ_{j}}$ (1.11)

其中 $m, α_{1} = 1, \dots, n$ 。令 $N_{α_{1} m} (ξ, ω^{s}) = {(N_{α_{1} 1 m} (ξ, ω^{s}), \dots, N_{α_{1} n m} (ξ, ω^{s}))}^{T}$ 。

为在 $Q^{s}$ 唯一定义 $N_{α_{1} m} (ξ, ω^{s})$ ，因此指定边界条件。

$N_{α m} (ξ, ω) = 0, ξ = \partial Q^{s}$ (1.12)

这样对任意 $ω^{s}$ 在每个 $Q^{s}$ 得到如下边值问题

${\begin{cases} \frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}})] = - \frac{\partial a_{i j m α_{1}} (ξ, ω^{s})}{\partial ξ_{j}} ξ \in Q^{s} \\ N_{α_{1} m} (ξ, ω^{s}) = 0 ξ \in \partial Q^{s} \end{cases}$ (1.13)

基于Lax-Milgram定理、Korn’s不等式和假设3，式1.13存在唯一解。方程1.8右边独立于ε，则方程1.8左边 $ε_{0}$ 的系数等于 $f_{i} (x)$ 有下式。

$\begin{array}{l} a_{i j h k} (ε, ω^{s}) \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) + a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}}) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{j}} \\ + \frac{1}{2} \frac{\partial}{\partial ξ_{j}} (a_{i j h k} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s})) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{k}} + \frac{1}{2} \frac{\partial}{\partial ξ_{j}} (a_{i j h k} (ε, ω^{s}) N_{α_{1} k m}^{s} (ε, ω^{s})) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{h}} \\ + \frac{\partial}{\partial x_{j}} [a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}} = f_{i} (x) \end{array}$ (1.14)

考虑到均匀化方程1.2，式1.14可重写为下式。

$\begin{array}{l} a_{i j h k} (ε, ω^{s}) \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) \\ + a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} k m} (ξ, ω^{s})}{\partial ξ_{h}}) - \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{j}} \\ + \frac{1}{2} \frac{\partial}{\partial ξ_{j}} (a_{i j h k} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s})) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{x_{k}}} + \frac{1}{2} \frac{\partial}{\partial ξ_{j}} (a_{i j h k} (ε, ω^{s}) N_{α_{1} α_{2} k m}^{s} (ε, ω^{s})) \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{x_{h}}} \\ + \frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}} \\ - {\hat{a}}_{i j h k} \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) + {\hat{a}}_{i j h k} \frac{1}{2} \frac{\partial}{\partial x_{j}} (\frac{\partial u_{k}^{0} (x)}{\partial x_{h}} + \frac{\partial u_{h}^{0} (x)}{\partial x_{k}}) = f_{i} (x) \end{array}$ (1.15)

由式1.15的 ${(a_{i j h k} (ε, ω^{s}))}_{n \times n}$ 对称性可得下式。

$\begin{array}{l} {\frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \\ - {\hat{a}}_{i α_{2} m α_{1}} + a_{i α_{2} m α_{1}} (ε, ω^{s}) + a_{i α_{2} h k} (ε, ω^{s}) \frac{\partial N_{α_{1} h m} (ε, ω^{s})}{\partial ξ_{k}} + \frac{\partial}{\partial ξ_{j}} (a_{i j h α_{2}} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s}))} \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}} \\ + {\hat{a}}_{i j h k} \frac{1}{2} \frac{\partial}{\partial ξ_{j}} (\frac{\partial u_{h}^{0} (x)}{\partial x_{k}} + \frac{\partial u_{k}^{0} (x)}{\partial x_{h}}) = f_{i} (x) \end{array}$ (1.16)

考虑到式1.1可得下式。

$\begin{array}{l} {\frac{\partial}{\partial ξ_{j}} [a_{i j h k} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \\ - {\hat{a}}_{i α_{2} m α_{1}} + a_{i α_{2} m α_{1}} (ε, ω^{s}) + a_{i α_{2} h k} (ε, ω^{s}) \frac{\partial N_{α_{1} h m} (ε, ω^{s})}{\partial ξ_{k}} \\ + \frac{\partial}{\partial ξ_{j}} (a_{i j h α_{2}} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s})))} \frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}} = 0 \end{array}$ (1.17)

既然 $\frac{\partial^{2} u_{m}^{0} (x)}{\partial x_{α_{1}} \partial x_{α_{2}}}$ ( $α_{1}, α_{2}, m = 1, \dots, n$ )不总是等于0，并且在每个单胞材料参数彼此独立，有下式成立。

${\begin{cases} \frac{\partial}{\partial ξ_{j}} [a_{i j h α_{1}} (ε, ω^{s}) \frac{1}{2} (\frac{\partial N_{α_{1} α_{2} h m} (ξ, ω^{s})}{\partial ξ_{k}} + \frac{\partial N_{α_{1} α_{2} k m} (ξ, ω^{s})}{\partial ξ_{h}})] \\ = {\hat{a}}_{i α_{2} m α_{1}} - a_{i α_{2} m α_{1}} (ε, ω^{s}) - a_{i α_{2} h k} (ε, ω^{s}) \frac{\partial N_{α_{1} h m} (ε, ω^{s})}{\partial ξ_{k}} - \frac{\partial}{\partial ξ_{j}} (a_{i j h α_{2}} (ε, ω^{s}) N_{α_{1} h m}^{s} (ε, ω^{s})) \\ N_{α_{1} α_{2} h m} (ε, ω^{s}) = 0 ξ \in \partial Q^{s} \end{cases}$ (1.18)

为定义在 $Q^{s}$ 的 $N_{α_{1} α_{2} h m} (ε, ω^{s})$ ，指定下式。

$N_{α_{1} α_{2} h m} (ε, ω^{s}) = 0$ (1.19)

对任意 $ω^{s}$ 在单胞 $Q^{s}$ 可获得下面问题。

虽然在 $Q^{s}$ 和 $Q^{t}$ ( $s \neq t$ )属于同一概率分布但彼此独立，对于样本 $ω^{s}$ ，则 $a_{i j h k} (ξ, ω^{s})$ ， $N_{α_{1} m} (ξ, ω^{s})$ ， $N_{α_{1} α_{2} m} (ξ, ω^{s})$ 不同于 $a_{i j h k} (ξ, ω^{t})$ ， $N_{α_{1} m} (ξ, ω^{t})$ ， $N_{α_{1} α_{2} m} (ξ, ω^{t})$ 同时，亦容易得出 $a_{i j h k} (ξ, ω^{s})$ ， $N_{α_{1} m} (ξ, ω^{s})$ ， $N_{α_{1} α_{2} m} (ξ, ω^{s})$ 是可测的随机变量。

方程1.19表示每一个单胞 $ε Q^{s}$ 的材料特性，两边积分的期望值为0，从而假设上述方程右边的积分期望值为0，有下面方程。

$\begin{array}{l} E [\int_{Q^{s}} {\hat{a}}_{i a_{2} m α_{1}} (ξ, ω^{s}) d ξ - \int_{Q^{s}} a_{i α_{2} m α_{1}} (ξ, ω^{s}) d ξ \\ - \int_{Q^{s}} a_{i α_{2} h k} (ξ, ω^{s}) \frac{\partial N_{α_{1} h m} (ξ, ω^{s})}{\partial ξ_{k}} d ξ - \int_{Q^{s}} \frac{\partial}{\partial ξ_{h}} (a_{i j h α_{2}} (ξ, ω^{s}) N_{α_{1} h m} (ξ, ω^{s})) d ξ] = 0 \end{array}$ (1.20)

考虑方程1.13固定边界则有下面方程。

$\int_{Q^{s}} \frac{\partial}{\partial ξ_{j}} (a_{i j h α_{2}} (ξ, ω^{s}) N_{α_{1} h m} (ξ, ω^{s})) d ξ = 0$ (1.21)

令：

${\hat{a}}_{i j h k} (ω^{s}) = \frac{1}{| Q^{s} |} \int_{Q^{s}} (a_{i j h k} (ξ, ω^{s}) + a_{i j p q} (ξ, ω^{s})) \frac{1}{2} (\frac{\partial N_{h p k} (ξ, ω)}{\partial ξ_{q}} + \frac{\partial N_{h q k} (ξ, ω)}{\partial ξ_{p}}) d ξ$ (1.22)

如果 ${\hat{a}}_{i j h k} (ω^{s})$ 的期望值存在，通过Kolmogorov强大数定理，可以用以下式子评估期望均匀化参数。

${\hat{a}}_{i j h k} = \frac{\sum_{s = 1}^{M} {\hat{a}}_{i j h k} (ω^{s})}{M} (M \to \infty)$ (1.23)

下面将证明 ${\hat{a}}_{i j h k} (ω^{s})$ 的期望值存在以及期望均匀化矩阵 ${{\hat{a}}_{i j h k}}$ 的对称正定性。要证明 ${\hat{a}}_{i j h k} (ω^{s})$ 期望值存在，由假设(1)，只需证明 ${\hat{a}}_{i j h k} (ω^{s})$ 有界。

证明：由假设(3)， $| a_{i j h k} (ξ, ω^{s}) | < M_{1}$ 。由式3.17，此方程有独立解 $N_{α 1} (ξ, ω^{s}) \in H^{1} (Q^{s})$ 满足下式1.24。

${‖ N_{α 1 h m} (ξ, ω^{s}) ‖}_{(H^{1} Q^{s})} < C {‖ a_{α 1 i j m} (ξ, ω^{s}) ‖}_{L^{\infty} (Q^{s})} < C M_{1}$ (1.24)

其中C和M₁是独立于ξ和ωs的常数。

通过式1.13和式1.24可以得到下式1.25。

$\begin{matrix} | {\hat{a}}_{i j h k} (ω^{s}) | = | \frac{1}{| m e s Q^{s} |} \int_{Q^{s}} (a_{i j h k} (ξ, ω^{s}) + a_{i j p q} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N_{h p k}}{\partial ξ_{q}} + \frac{\partial N_{h q k}}{\partial ξ_{p}}) d ξ) | \\ < \frac{1}{| m e s Q^{s} |} ({‖ a_{i j h k} (ξ, ω^{s}) ‖}_{L^{\infty} (Q^{s})} + {‖ a_{i j h k} (ξ, ω^{s}) ‖}_{L^{\infty} (Q^{s})} {‖ N_{α 1 h m} (ξ, ω^{s}) ‖}_{H^{1} (Q^{s})}) \\ \leq \frac{1}{| m e s Q^{s} |} | M_{1} + M_{2} \times C M_{1} | | m e s Q^{s} | = (C + 1) M_{1}^{2} = M_{3} \end{matrix}$ (1.25)

其中 $M_{3} = (C + 1) M_{1}$ 和 $M_{3}$ 是独立于 $ξ$ 和 $ω^{s}$ 的常数。因此，由假设(1)此处存在期望值 $E {\hat{a}}_{i j h k} (ω^{s})$ 。接着证明矩阵 ${{\hat{a}}_{i j h k}}$ 对称正定。

证明：类比周期的思想，容易证明 ${({\hat{a}}_{i j h k} (ω^{s}))}_{n \times n}$ 是对称正定的，即有下式1.26。

${\hat{a}}_{i j h k} (ω^{s}) = {\hat{a}}_{j i k h} (ω^{s}) = {\hat{a}}_{i j k h} (ω^{s})$ 和 $c_{1} η_{i h} η_{i h} \leq {\hat{a}}_{i j h k} (ω^{s}) η_{i j} η_{h k} \leq c_{2} η_{i h} η_{i h}$ (1.26)

由于 $a_{i j h k} (ω^{s})$ 的期望值存在，可以得到下式1.27。

$E {\hat{a}}_{i j h k} (ω^{s}) = E {\hat{a}}_{j i k h} (ω^{s}) = E {\hat{a}}_{i j k h} (ω^{s})$ 和 $c_{1} η_{i h} η_{i h} \leq E {\hat{a}}_{i j h k} (ω^{s}) η_{i j} η_{h k} \leq c_{2} η_{i h} η_{i h}$ (1.27)

因此期望均匀化力学参数和期望均匀化方程存在，而且 ${{\hat{a}}_{i j h k}}_{n \times n}$ 是对称正定的，满足前面假设。

以上是根据已有研究成果所得的部分推导，可得到如下定理。

定理：随机分布复合材料的弹性力学问题的位移解有下面形式得双尺度展开式。

$u^{ε} (x, ω) = u^{0} (x) + ε N_{α 1} (ξ, ω) \frac{\partial u^{0} (x)}{\partial_{x_{α 1}}} + ε^{2} N_{α 1 α 2} (ξ, ω) \frac{\partial^{2} u (x)}{\partial^{2}_{x_{α 1} x_{α 2}}} + ε^{3} P_{1} (x, ξ, ω)$ (1.28)

其中 $u_{0} (x)$ 是式1.2期望均匀化解。 $N_{α_{1}} (ξ, ω)$ 和 $N_{α_{1} α_{2}} (ξ, ω)$ 分别是式1.13和式1.19的解。

2.2. 基于双尺度分析的多尺度算法

按照具有多种尺度颗粒的沥青混合料把集料(1.18~2.36 mm、2.36~4.75 mm、4.75~9.5 mm、9.5~13.2 mm、13.2~16 mm)分成多个尺度，然后确定每类集料所适合的尺度模型，从小粒径集料逐级均匀化至大粒径集料，用双尺度方法递推地计算最终的期望均匀化参数。现在给出计算复合材料力学性能参数双尺度方法流程。

1) 首先假设基体材料的力学参数为 ${a_{i j h k}}$ ，颗粒增强材料的力学参数为 ${{a^{'}}_{i j h k}}$ 。计算第m尺度下的期望均质化参数 ${\hat{a}}_{i j h k} (ε^{m})$ 。

(a) 基于m尺度颗粒的统计规律， $\forall ω^{s}$ 具有颗粒的样本被生成，它的力学性能参数 $a_{i j h k} (\frac{x}{ε^{m}}, ω^{s})$ ， $\forall ε^{m} Q^{s} (ε^{m})$ 可以被定义式1.29。

$a_{i j h k} (\frac{x}{ε^{m}}, ω^{s}) = {\begin{cases} a_{i j h k} x = ε^{m} {\hat{Q}}^{s} \\ {a^{'}}_{i j h k} x = ε^{m} {\tilde{Q}}^{s} \end{cases}$ (1.29)

其中有 $ε^{m} {\hat{Q}}^{s} \cup ε^{m} {\tilde{Q}}^{s} = ε^{m} Q^{s}$ 和 $ε^{m} {\hat{Q}}^{s} \cap ε^{m} {\tilde{Q}}^{s} = ϕ$ ， $ε^{m} {\hat{Q}}^{s}$ 是 $ε^{m} Q^{s}$ 中的基体， $ε^{m} {\tilde{Q}}^{s}$ 是 $ε^{m} Q^{s}$ 中的颗粒增强材料。

(b) 从材料系数 $a_{i j h k} (\frac{x}{ε^{m}}, ω^{s})$ 通过有限元方法解方程得到 $N_{α 1 m} (\frac{x}{ε^{m}}, ω^{s})$ ，然后通过下式3.34。

$N_{α_{1}} (ξ, ω^{s}) = (\begin{array}{l} N_{α_{1} 11} (ξ, ω^{s}) \dots N_{α_{1} 1 n} (ξ, ω^{s}) \\ ⋮ ⋱ ⋮ \\ N_{α_{1} n 1} (ξ, ω^{s}) \dots N_{α_{1} n n} (ξ, ω^{s}) \end{array})$ (1.30)

$N_{α_{1}} (ξ, ω^{s})$ 是函数矩阵；可以得到此样本均匀化系数 ${\hat{a}}_{i j h k} (\frac{x}{ε^{m}}, ω^{s})$ 。

(c) 对 $ω^{s}$ ， $s = 1, 2, \dots, M^{m}$ ，(a)和(b)重复 $M^{m}$ ，可以得到 $M^{m}$ 个均匀化系数 ${\hat{a}}_{i j h k} (\frac{x}{ε^{m}}, ω^{s})$ ( $s = 1, 2, \dots, M^{m}$ )，这样就可以计算具有颗粒尺度小于 $ε^{m}$ 的材料期望均匀化系数 ${\hat{a}}_{i j h k} (ε^{m})$ 。

${\hat{a}}_{i j h k} (ε^{m}) = \frac{\sum_{s = 1}^{M^{m}} {\hat{a}}_{i j h k} (\frac{x}{ε^{m}}, ω^{s})}{M^{m}}$ (1.31)

2) 如果 $γ = m - 1, m - 2, \dots, 1$ ，可以按递归方法求出每个尺度的均匀化系数 ${\hat{a}}_{i j h k} (ε^{γ})$ 。

(a) 同上基于第γ尺度颗粒分布特征的统计规律得到颗粒各种参数的分布形式，然后用计算机模拟得到它的样本 $ω^{s}$ ，从而可以得到材料力学性能参数，它们是随机函数 $a_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})$ 的一个样本。

$a_{i j h k} (\frac{x}{ε^{γ}}, ω^{s}) = {\begin{cases} {\hat{a}}_{i j h k} (ε^{γ + 1}) x = ε^{γ} {\hat{Q}}^{s} \\ {a^{'}}_{i j h k} x = ε^{γ} {\tilde{Q}}^{s} \end{cases}$ (1.32)

其中有 $ε^{γ} {\hat{Q}}^{s} \cup ε^{γ} {\tilde{Q}}^{s} = ε^{γ} Q^{s}$ 和 $ε^{γ} {\hat{Q}}^{s} \cap ε^{γ} {\tilde{Q}}^{s} = ϕ$ ， $ε^{γ} {\hat{Q}}^{s}$ 是单胞 $ε^{γ} Q^{s}$ 中的基体即在前一步(m尺度下)计算的期望均匀化参数； $ε^{γ} {\tilde{Q}}^{s}$ 是 $ε^{γ} Q^{s}$ 中的颗粒增强材料。

(b) 从材料系数 $a_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})$ 通过有限元方法解方程得到 $N_{α 1 m} (\frac{x}{ε^{m}}, ω^{s})$ ，然后通过下式3.37。

$N_{α_{1}} (ξ, ω^{s})$ 是函数矩阵；可以得到此样本均匀化系数 ${\hat{a}}_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})$ 。

(c) 对 $ω^{s}$ ， $s = 1, 2, \dots, M^{γ}$ ，(a)和(b)重复 $M^{γ}$ ，可以得到 $M^{γ}$ 个均匀化系数 ${\hat{a}}_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})$ ( $s = 1, 2, \dots, M^{γ}$ )，这样就可以计算具有颗粒尺度小于 $ε^{γ}$ 的材料期望均匀化系数 ${\hat{a}}_{i j h k} (ε^{γ})$ 。

${\hat{a}}_{i j h k} (ε^{γ}) = \frac{\sum_{s = 1}^{M^{γ}} {\hat{a}}_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})}{M^{γ}}$ (1.34)

3) 最后，均匀化系数 ${\hat{a}}_{i j h k} = {\hat{a}}_{i j h k} (ε^{1})$ 是在 $Ω$ 上的期望均质化系数(等效力学性能参数)。其中本文所得到的均匀化参数为弹性模量E及泊松比μ。

3. 多尺度算法流程

选取多种尺寸的尺度窗口计算各类沥青混合料的刚度参数，在研究初期尽可能多地选取不同尺度窗口计算材料刚度参数以保证预测结果的准确性。1.18 mm以下集料与沥青结合体称为沥青砂，1.18 mm以上集料则可建立其细观结构体现在模型中。

本文探究AC-13C及M_9.5~13.2、M_4.75~9.5、M_2.36~4.75、M_1.18~2.36沥青混合料多尺度建模方法；其重点内容在于两个方面，第一各类沥青混合料集料随机分布；第二沥青混合料计算尺度的选取。对于各类沥青混合料而言集料的粒径是确定的，AC-13C其公称最大粒径13.2 mm，M_9.5~13.2其公称最大粒径9.5mm，M_4.75~9.5其公称最大粒径4.75 mm，M_2.36~4.75其公称最大粒径2.36 mm，M_1.18~2.36公称最大粒径为1.18 mm；按照尺度等级把各类沥青混合料分为五个尺度，然后确定每类粒径骨料在当前尺度下的分布，一级一级地均匀化材料，用双尺度方法逐级地计算预测各类沥青混合料期望均质化参数。

简要说明双尺度方法在计算机实现的流程：

在Abaqus有限元软件建立正方形细观尺度模型；

将模型划分为三角形单元，导出单元编号、节点坐标、边界节点等文本信息；

编制Matlab程序导出材料文本信息；

编制C++程序用于均匀化尺度模型材料文本信息，得出双尺度均匀化参数E、μ值。图1为多尺度算法的计算机操作流程。

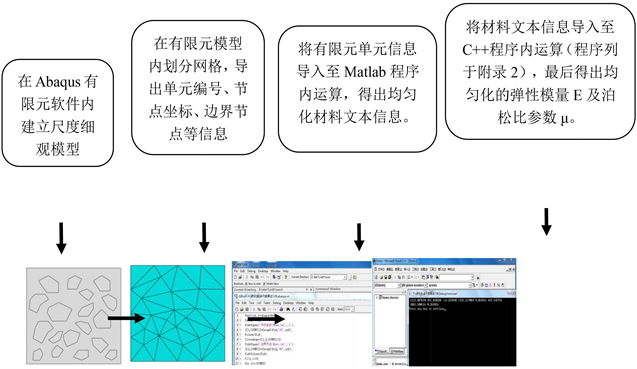
Figure 1. Computer operation process of multi-scale algorithm

图1. 多尺度算法的计算机操作流程

4. 基于多尺度算法预测材料刚度参数方法

4.1. 多尺度算法等效力学参数预测过程

为获取含不同粒径集料沥青混合料刚度参数，需要逐级均匀化各类沥青混合料尺度模型以预测沥青混合料力学参数，以下是多尺度算法的等效力学参数预测过程。

Step 1：确定含不同粒径集料沥青混合料的尺度数目m (m = 1, 2, 3, 4, 5)以及用于计算均匀化循环次数γ (γ = 1, 2, 3, 4, 5)，沥青混合料尺度数目等于均匀化循环次数；

Step 2：统计各类沥青混合料骨料特性得出确定随机颗粒的概率分布以及相关尺寸，按照相应的随机分布 $F_{γ}, γ = 1, 2, \dots, m$ ；并生成相应的随机数；

Step 3：在选定尺度区域 $Q_{γ}^{S}$ 内，模拟第m尺度的随机颗粒；

Step 4：输入粒径颗粒(某档集料)在区域 $Q_{γ}^{S}$ 中所有参数的概率分布，如径长、边形数、颗粒中心点分布；

Step 5：依据上述随机分布，在区域 $Q_{γ}^{S}$ 内生成随机颗粒，并满足颗粒之间彼此不接触；

Step 6：根据图1双尺度均匀化流程在区域 $Q_{γ}^{S}$ 内建立模型及划分网格，导出网格内单元编号、节点坐标、边界节点等信息；

Step 7：当 $γ = m$ ，在区域 $Q_{γ}^{S}$ 中，可以按照如下式3.1决定力学参数 $a_{i j h k} (\frac{x}{ε^{γ}}, ω^{s})$ ；

$a_{i j h k} (\frac{x}{ε^{γ}}, ω^{s}) = {\begin{cases} a_{i j h k}^{1}, x \in ε {\hat{Q}}^{s} \\ a_{i j h k}^{2}, x \in ε {\tilde{Q}}^{s} \\ ⋮ \\ a_{i j h k}^{l}, x \in ε {\overset{⌢}{Q}}^{s} \end{cases}$ (3.1)

其中 ${\hat{Q}}^{s} \cup {\tilde{Q}}^{s} \cup \dots \cup {\overset{⌢}{Q}}^{s} = Q_{γ}^{s}$ 和 ${\hat{Q}}^{s} \cap {\tilde{Q}}^{s} \cap \dots \cap {\overset{⌢}{Q}}^{s} = ϕ$ ， $ε Q_{γ}^{s} \subset Ω$ 为模拟材料的区域， $ε Q_{γ}^{s}$ 为基体区域， $ε {\tilde{Q}}^{s}$ 为复合材料的增强颗粒区域， $ε {\overset{⌢}{Q}}^{s}$ 为颗粒与基体交际带区域。

Step 8：根据以下式3.2；

${\hat{a}}^{h_{0}}_{i j h k} (ω^{s}) = \frac{1}{| m e s Q^{s} |} \int_{Q^{s}} (a_{i j h k} (ξ, ω^{s}) + a_{i j p q} (ξ, ω^{s}) \frac{1}{2} (\frac{\partial N^{h_{0}}_{h p k} (ξ, ω^{s})}{\partial ξ_{q}} + \frac{\partial N^{h_{0}}_{h q k} (ξ, ω^{s})}{\partial ξ_{p}}) d ξ)$ (3.2)

计算第γ层尺寸样本的均匀化力学参数 ${\hat{a}}_{i j h k}^{h_{0}} (ε^{γ}, ω^{s})$ ，最后根据 ${\hat{a}}_{i j h k}^{h_{0}} = \frac{\sum_{s = 1}^{M} {\hat{a}}_{i j h k}^{h_{0}} (ω^{s})}{M}$ 计算等效力学参数 ${{\hat{a}}_{i j h k}^{h_{0}} (ε^{γ})}$ 。

Step 9：令 ${\hat{a}}_{i j h k} (ε^{γ + 1})$ 等于 ${\hat{a}}_{i j h k}^{h_{0}} (ε^{γ + 1})$ ，然后设γ = γ + 1，如果γ > 1，返回Step 2逐级计算γ = 1，2，…m的等效力学参数。

4.2. 基于多尺度算法预测沥青混合料刚度参数流程

基于多尺度算法预测沥青混合料刚度参数需要建立符合沥青混合料骨料分布尺度模型，然后从小粒径集料的尺度模型均匀化预测刚度参数E、μ；将小粒径模型均匀化后的刚度参数E、μ代入至下一粒径模型的基体内，经算法预测下一粒径的刚度参数；重复该方法逐层预测各类沥青混合料参数，图2是沥青混合料刚度参数预测流程。

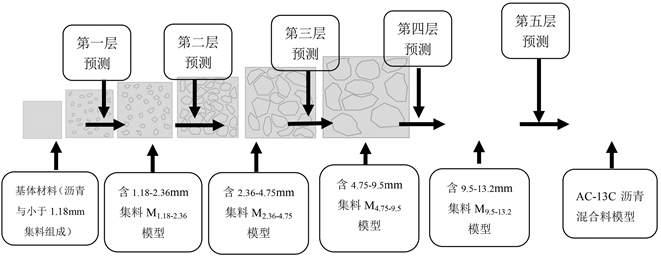
Figure 2. Prediction process for stiffness parameters of asphalt mixture

图2. 沥青混合料刚度参数预测流程

应用多尺度算法逐步预测含1.18~2.36 mm集料M_1.18~2.36沥青混合料、含2.36~4.75 mm集料M_2.36~4.75沥青混合料、含4.75~9.5 mm集料M_4.75~9.5沥青混合料、含9.5~13.2 mm集料M_9.5~13.2沥青混合料及AC-13C沥青混合料的刚度参数，并分析预测过程沥青混合料刚度参数预测结果是否满足有效性要求，根据已有研究表明多尺度算法结果与试验值误差在10%以内时计算结果能满足工程需要。

AC-13C经多尺度算法预测的刚度结果误差范围小于1%，其刚度结果能符合回弹测试值的精度要求；由M_9.5~13.2、M_4.75~9.5、M_2.36~4.75、M_1.18~2.36误差结果表明随骨料尺寸增大误差在不断减低，尺度计算结果与劈裂回弹试验值更为吻合，证明了骨料对沥青混合料弹性模块影响程度较大，骨料掺入能提高沥青混合料的弹性模量。

5. 结论

本文建立符合各类沥青混合料骨料特性的二维细观模型，接着提出多尺度算法理论及算法流程。

获得的主要结论如下：

1) 含不同粒径集料沥青混合料经多尺度算法预测的刚度参数结果在众多样本的计算后其结果趋于收敛，经分析可知多尺度算法所得的弹性模量与劈裂回弹模量测试得到的模量参数误差在5%以内能够满足工程计算的需要。

2) 由上文含不同粒径集料沥青混合料刚度参数预测结果显示，在经过均匀化后沥青混合料刚度参数E、μ能够趋于收敛状态；同时对比多尺度算法预测结果与尺度计算结果能满足工程需要。

3) 提出了复合材料力学参数的多尺度算法，推导出基于双尺度分析的多尺度算法的数学表征及其双尺度计算流程。

基金项目

国家自然科学基金资助项目(51978080)。

参考文献

[1]	李霄琳. 非均质材料的光滑多尺度有限元法研究[D]: [博士学位论文]. 长春: 吉林大学, 2015.
[2]	武亚涛. 随机非均匀材料性能分析的多尺度算法研究[D]: [博士学位论文]. 西安: 西北工业大学, 2015.
[3]	冯永平. 复合材料结构多场耦合问题多尺度方法及其有限元算法[D]: [博士学位论文]. 北京: 中国科学院, 2003.
[4]	冯永平, 崔俊芝, 邓明香. 周期孔洞区域中热力耦合问题的双尺度有限元计算[J]. 物理学报, 2009, 58(z1): 327-337.
[5]	连尉平, 崔俊芝. 三维编织复合材料模量的双尺度有限元计算[J]. 计算力学学报, 2005, 22(3): 268-273+286.
[6]	陈玉丽, 马勇, 潘飞, 等. 多尺度复合材料力学研究进展[J]. 固体力学学报, 2018, 39(1): 1-68.
[7]	储辰辰, 蔡恒, 叶俊杰, 等. 多尺度方法预测复合材料层板裂纹扩展[J]. 西安电子科技大学学报(自然科学版), 2017, 45(3): 53-58.
[8]	许杨剑, 武鹏伟, 赵帅, 等. 弹塑性多尺度分析的实现及其在颗粒增强复合材料中的应用[J]. 复合材料学报, 2017, 34(9): 1934-1943.
[9]	方光武, 宋迎东, 高希光. 层合陶瓷基复合材料多尺度应力——应变计算模型[J]. 航空动力学报, 2017, 32(6): 1375-1380.
[10]	李力, 赵海涛, 陈吉安, 等. 基于多尺度方法的纤维织物增强柔性复合材料拉伸模量预测[J]. 复合材料学报, 2016, 33(10): 2312-2318.
[11]	裴世源, 徐华. 非均质复合材料力学性能的确定性多尺度计算方法[J]. 西安交通大学学报, 2015, 49(10): 8-13.
[12]	潘裕清. 随机复合材料粘弹性能的双尺度计算方法[D]: [硕士学位论文]. 长沙: 长沙理工大学, 2013.
[13]	李友云, 崔俊芝, 郑健龙. 颗粒随机分布复合材料物理与力学性能的多尺度分析方法[M]. 长沙: 湖南科学技术出版社, 2013: 60-97.

为你推荐

友情链接