1. 引言
整值时间序列是对按时间顺序发生的事件的计数,出现在许多实际场景中。例如,每年飓风发生的数量、物种每年的繁殖数量、保险公司每月的理赔数量、股票的交易数量等。Mckenzie [1] 提出了基于二项稀疏算子的建模思路,用一个细化运算符来代替经典时间序列模型中的标量乘法,从而实现对整值数据建模与分析的目的。20世纪80年代末,Al-Osh等 [2] 基于二项稀疏算子建立了一阶整数值自回归(INAR(1))过程及一阶整数值移动平均(INMA(1))过程,开启了整数值时间序列研究的先河。随后发展出了各类整值时间序列模型 [3] [4] 。
随着现代科学技术的飞速发展,收集和储存的数据规模越来越庞大。在处理海量数据时,构造的数据矩阵的维数也越来越大,从而极大地促进了大维数据矩阵的研究。经典的中心极限定理不再适用于大维随机矩阵,而降维又会导致数据信息的丢失。经过众多学者的努力,发展出了能有效处理大维数据矩阵的随机矩阵理论。近年来,随机矩阵理论在核物理、流体力学、图像处理等领域得到了广泛应用 [5] 。
在处理大维海量数据时,一个重要的研究方向是大维随机矩阵的谱分析。上世纪50年代,Wigner [6] [7] 将随机矩阵与量子物理结合起来研究核物理,发现了随机Wigner矩阵,并证明了Wigner矩阵标准化后的经验谱分布函数的期望收敛到半圆律。随后Marcenko和Pastur [8] 在随机矩阵所有元素互相独立的条件下推导出了大维样本协方差矩阵的极限谱分布。为弱化矩阵中元素之间的独立性假设,Silverstein [9] 考虑了
的情况,其中T表示Hermitian矩阵,Y表示元素相互独立的随机向量。Bai和Zhou [10] 利用Stieltjes变换研究了只有列向量相互独立的大维样本协方差矩阵的极限谱分布。胡江 [11] 等人将此方法应用于推导具有AR(1)过程依赖结构的随机矩阵的极限谱分布。Pfaffel和Schlemm [12] 将此方法进一步扩展到具有线性元素的随机矩阵的极限谱分布的研究中,推导出了样本协方差极限谱分布的Stieltjes变换形式。文献 [13] 利用Pfaffel和Schlemm发展出的理论,给出了具有ARMA(p, q)过程依赖结构的随机矩阵的极限谱密度。然而,整数值时间序列模型都是非线性的,无法直接利用文献 [13] 的理论给出INMA(1)型随机矩阵的极限谱分布。
本文研究了具有INMA(1)结构的大维随机矩阵的极限谱分布。主要研究思路如下:首先通过对INMA(1)过程的研究得,INMA(1)过程表示为一类特殊的线性过程;然后基于线性表示此证明具有INMA(1)结构的大维随机矩阵样本协方差矩阵的极限谱分布存在;其次利用Stieltjes变换给出了具有INMA(1)结构的大维随机矩阵样本协方差矩阵的极限谱密度函数;最后通过数值模拟,绘制直方图并与理论结果对比,验证本文方法的有效性。
2. 基本概念及性质
2.1. INMA(1)过程及其样本协方差矩阵
20世纪80年代末,Al-Osh等 [2] 基于二项稀疏算子构建了INMA(1)过程。具体而言,称满足如下形式的随机变量序列
是INMA(1)过程,
(1)
其中,
是相互独立的伯努利随机变量序列,
,
,
是独立同分布的泊松随机变量序列,满足
,且
与
独立,记号“
”表示二项稀疏算子 [14] 。
性质1.1. [15] 满足上述定义的随机变量序列
是平稳的,其均值、方差、自协方差函数分别如下所示:
性质1.2. 令
表示
的功率谱密度函数,则
。
证明 由性质1.1可得
。
证毕。£
称
为具有INMA(1)结构的随机矩阵,若
的每一行
是由INMA(1)过程生成的
其中,各行之间元素是相互独立的。
的样本协方差矩阵为:
,
其中,
。
2.2. 极限谱密度及Stieltjes变换
记
为p阶样本协方差阵
的p个特征根,称
是矩阵
的经验谱分布函数。当
时,若
存在且是非随机的,则称其为
的极限谱分布。
的Stieltjes变换为
,
其中,I为p阶单位阵。tr(·)表示矩阵的迹。
3. 主要结果及证明
3.1. 具有INMA(1)结构的随机矩阵的极限谱密度
由于均值不影响
的极限谱分布 [16] ,所以对
极限谱分布的求解可以简化为对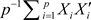 极限谱分布的求解。在下文中,我们仍令
。记
,其对应极限谱分布的Stieltjes变换形式为
。下文简记
,
。下面给出本文主要结论。
极限谱分布的求解。在下文中,我们仍令
。记
,其对应极限谱分布的Stieltjes变换形式为
。下文简记
,
。下面给出本文主要结论。
定理2.1. 设
是INMA(1)型随机矩阵的样本协方差矩阵,若
是相互独立的,其均值为0,方差为
,当
时,
,
以概率1收敛到一个非随机概率分布F,该分布Stieltjes变换满足
, (2)
其中,
。
定理2.2. INMA(1)型随机矩阵的样本协方差矩阵
的极限谱分布F的Stieltjes变换是关于z的函数。记
,
其中
,
,
为定理2.1中式(2)的四个解,则INMA(1)型随机矩阵的样本协方差矩阵
的极限谱密度为
。
3.2. 定理2.1的证明
为了证明定理2.1,我们需要用到如下引理。
引理2.1. [8] 设
是
的随机矩阵,且
的第i行满足
,
其中
是独立随机变量数组且满足:
以及对所有的
,有当
时,
(Lindeberg型条件)。
则
可以表示为线性过程,并且具有连续可微的谱密度f。若进一步满足下述条件:
存在正数C和
,对所有
有
;
对所有
,只有有限个
是
的根;
对几乎所有的
,
。
则当
时,
的经验谱分布几乎必然收敛到一个具有有界支撑的非随机概率分布F,且存在正数
和
,使得F的Stieltjes变换
是满足如下方程的唯一
的映射
。
由引理2.1可知,当随机矩阵内部满足线性结构时,其生成样本协方差阵的极限谱分布存在并可以用Stieltjes变换表示。对于具有INMA(1)结构的随机矩阵来说,由于INMA(1)中的二项稀疏算子是非线性的,我们不可以直接使用引理2.1。下面首先证明INMA(1)过程可以进行线性表示。
证明 对任意
,
,令
,
其中
是独立同分布的。
则
。
由文献 [12] 可知,如果潜在的线性过程具有非零平均值,即
,引理2.1仍然有效。所以
可以表示成线性过程。下面证明
满足引理2.1的条件。
当
时,则有
,
,
当
时,则
。
对所有的
,当
时,由Holder不等式和切比雪夫不等式得
,
其中
。
由上述证明知
的每一行元素可表示为随机线性序列。注意到
。
和
都有
成立。因此引理2.1中的条件1满足。由性质1.2可知,
是有理函数,对于
满足
的根只有有限多个,引理2.1中的条件2、3满足。
由引理2.1可知,当
时,样本协方差矩阵
的极限谱分布F存在,且存在正数
使得F的Stiltjes变换是满足如下方程的唯一映射
。
由文献 [17] 可知,上式等价于
,
将谱密度
代入,得
,
其中,m是
对应极限谱分布的Stieltjes变换,
是
对应极限谱分布的Stieltjes变换,满足
证毕。£
3.3. 定理2.2的证明
根据留数定理,(2)式中积分部分可表示为:
。
则
是如下方程的唯一的解
。
上式可转化为如下的一元四次方程:
由文献 [11] 可知方程的4个根为
其中,
为了证明定理2.2,我们需要用到如下引理。
引理2.2. [17] 对于每一个
,都存在
其中,函数
在
上是连续的,并且F在
上有连续导函数f,
。密度函数f对于每一个
,
都是解析的。并且其中的
,
是满足等式(2)的唯一
的虚部。
根据上述留数定理的推导结果,可以得到关于
的四个解。通过公式
,容易得到
,
,将
,
代入引理2.2的公式
中,得到密度函数的四个解
,
,选取
,
中函数值大于0的密度函数组成新密度函数
得到INMA(1)型随机矩阵的样本协方差矩阵
的极限谱密度。即
。
证毕。£
4. 数值模拟
本节通过数值模拟对本文结论进行检验。基于式(1),模拟生成5000个服从INMA(1)过程的随机数序列。
是相互独立的伯努利随机变量序列,
,且
与
独立。INMA(1)型随机矩阵的样本协方差矩阵
的极限谱分布的Stieltjes变换是关于参数
和
的函数。首先假设
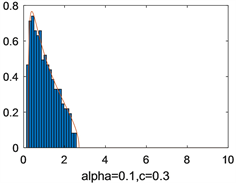
,绘制频率直方图和极限谱密度见图1。图1左侧是
的图像,右侧是
的图像。阴影部分是基于特征根绘制的频率直方图,红色曲线是由定理2.2得到的INMA(1)型随机矩阵的极限谱密度函数。从图1可以看出,理论结果与数值模拟结果相一致。进一步地,我们分别绘制了在
,
和
时,INMA(1)型随机矩阵的样本协方差矩阵
的极限谱分布的密度函数,其结果见图2。从图2可知,随着
的增大,图像的峰值会随之上升。
 (a)
(a) 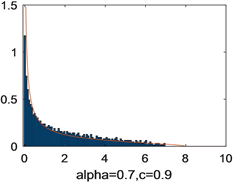 (b)
(b)
Figure 1. Histograms of eigenvalues and limiting spectral density
图1. 特征值和极限谱密度的直方图
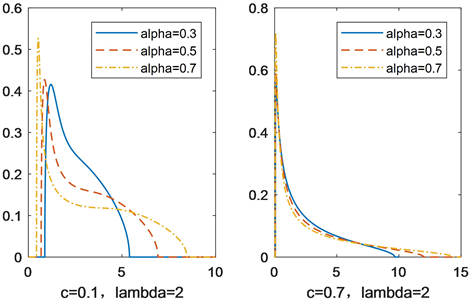
Figure 2. Limiting spectral density of INMA(1) type random matrix under different parameters
图2. INMA(1)型随机矩阵不同参数下的极限谱密度
本文主要探讨了两个问题,第一个是INMA(1)过程的线性表示,第二个是基于线性表示推导了具有INMA(1)结构随机矩阵的极限谱密度,并通过数值模拟验证理论结果。通过对INMA(1)过程的研究发现,INMA(1)的相关结构与连续情形下的MA(1)过程类似。特别地,当INMA(1)过程
时,就变为了MA(1)过程,即
。分别绘制了INMA(1)过程和MA(1)过程的极限谱密度函数图像见图3。其中,左侧设置INMA(1)参数为
,右侧MA(1)过程参数为
。通过比较发现,MA(1)过程相比INMA(1)过程更靠近原点,INMA(1)过程的峰值比MA(1)过程低。这说明INMA(1)过程极限谱分布的尾概率大于MA(1)过程极限谱分布的尾概率。
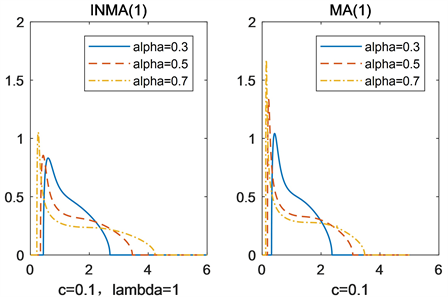
Figure 3. Limiting spectral density of INMA(1) process and MA(1) process
图3. INMA(1)过程和MA(1)过程的极限谱密度
结合大维随机矩阵的样本协方差矩阵的极限谱分布函数和经验谱分布函数,可以构造出相关统计量用于假设检验。例如:原假设为
时,原观测序列的极限谱密度是MP律;原假设为
时,观测序列的差序列
的极限谱密度是MP律。若经验谱密度和MP律的差异越小,则接受原假设的可能性越大。特别地,以经验谱密度和MP律的差的绝对值构造一个积分检验统计量,结合自助法可以得到该积分检验统计量的经验分布和P值,从而实现假设检验的目的。另一方面,对于观测序列是否服从INMA(1)这一假设检验问题,可以先利用序列估计INMA(1)过程,结合定理2.2可得到该估计INMA(1)过程的极限谱密度,同样的,利用经验谱密度和极限谱密度的差的绝对值构造一个积分检验统计量,结合自助法得到该积分检验统计量的经验分布和P值,从而对上述问题进行检验。
基金项目
基于相依整值随机场和深度学习的人类突发行为建模和预测(RD2300002084)。
NOTES
*通讯作者。