航天器相对位姿一体化的自调整控制方法

Self-Adjusting Control Method of Integrated Relative Position and Attitude of Spacecraft

摘要: 航天器间姿态与轨迹的耦合效果对于航天器在太空中的交会有着较大的影响。针对传统航天器在追踪问题上无法统一描述姿轨耦合与减小控制力、控制力矩饱和的问题，本文提出了一种自调整函数的改进型PD控制方法，更好地实现了航天器姿态与轨道的一体化控制，确保了航天器在追踪条件下的自身姿轨与追踪目标姿轨的同步性。本文利用Lyapunov函数对姿轨耦合系统进行稳定性分析，实验结果证明了本文所提方法在系统稳定性和饱和性上具有较好的控制效果。

Abstract: The coupling effect of attitude and trajectory between spacecraft has a great influence on spacecraft rendezvous in space. Aiming at the problems that traditional spacecraft cannot uniformly describe the coupling of attitude and orbit, reduce the control force and saturated control moment, this pa-per proposes an improved PD control method with self-adjusting function, which better realizes the integrated control of spacecraft attitude and orbit, and ensures the synchronization of spacecraft self-attitude orbit and target attitude orbit under tracking conditions. In this paper, Lyapunov func-tion is used to analyze the stability of the asis-orbit coupling system. The experimental results show that the proposed method has a good control effect on the stability and saturation of the system.

1. 引言

近年来，随着科技的不断发展，航天技术在基础理论、技术应用研究以及工程应用上取得了显著的突破 [1] 。高效的航天器轨道和姿态的耦合控制在航天任务中占据着重要地位，国内外学者进行了大量的航天器姿轨控制研究。

传统的航天器交会控制方法是分别建立单独的姿态或轨道控制，完成航天器的交会与航行任务。杨一岱等人在航天器平动与转动的基础上添加了挠性振动控制，对航天器姿态运动产生较大的影响 [2] 。Gong等人通过设计太阳帆的惯性，得到了耦合动力学方程的平衡点，而耦合平衡点的稳定性分别由姿态平衡点和轨道平衡点的稳定性决定 [3] 。刘向东等人设计了基于多智能体的姿态协调控制 [4] ，完善了在编队飞行跟踪姿态上的同步性。上述的几种控制中多是基于姿态或者轨迹的单方面的控制方法研究，忽略了姿轨耦合运动对航天器交会控制的影响，即使是将其一作为扰动量代入，也会无法满足航天器同步交会对接的精度要求。

在面向航天器间交会与编队飞行等近距离跟踪任务时，由于需要记录并反馈目标航天器的实时姿轨信息，迫切需要一种将传统的单一姿轨控制相结合为耦合控制，以此来满足位姿一体化控制的基本需求。Koji Yamanak在小型卫星编队飞行上应用了姿态和轨道组合控制律 [5] ，实现了小型卫星上的姿态与轨道的协同控制。Krogstad在深空探索航天器上应用一种基于6自由度的同步姿轨控制方案 [6] ，该方法在姿轨控制上具有较好的效果。Filipe和Tsiotras开发了一种基于航天器交会的耦合旋转–平移控制方法 [7] ，该方法对于航天器的姿轨耦合控制具有较好的控制效果。对偶四元数可以将姿态与轨迹统一在一个控制系统模型中，且与四元数在描述姿态运动时的数学性质非常类似，可以很好的消除姿态解算的奇异性。

本文的创新点是在PD控制的基础上加入了自调整函数，可以很好的减小控制实验中控制力与控制力矩的饱和性，缩短了控制实验进入稳定状态的时间。实验结果证明了自调整后的PD控制在航天器姿轨耦合控制上具有较好的效果。

2. 理论分析

2.1. 坐标描述

本文设计的航天环境为两航天器间跟踪的相对位姿一体化，分为领航航天器Leader和追踪航天器Follower，将两个航天器看作刚体结构(视为两个质点)，指向不变的惯性坐标系是地球O₁-XYZ，而O₂-XYZ与O₃-XYZ两坐标是领航、追踪航天器质点位置变化的本体坐标系， $r_f$ 与 $r_l$ 分别表示两坐标系间的相对位置信息，即惯性坐标指向领航与追踪航天器的本体坐标。Leader与Follower两航天器间的平动–旋转矢量即为两航天器本体坐标的相对运动，如图1所示。

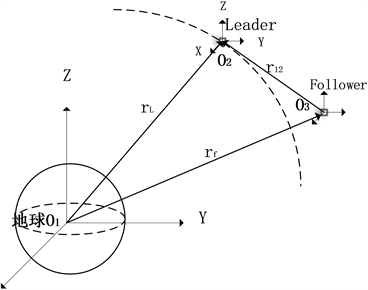
Figure 1. Schematic diagram of spacecraft tracking

图1. 航天器追踪示意图

2.2. 姿轨耦合运动学模型

Clliford [8] 提出对偶数公式为

$\hat{a}=a+\epsilon a^{\prime }$ (1)

$a,a^{\prime }$ 都是实数，a是对偶数的实部， $a^{\prime }$ 是对偶数的虚部， $\epsilon$ 是对偶单位，且 ${\epsilon }^2=0$ 。

对偶四元数定义为

$\hat{q}=q+\epsilon q^{\prime }$ (2)

q与 $q^{\prime }$ 都为普通的四元数。依据(2)式与姿态运动 [9] 可以得出

$\hat{q}=q_e+\epsilon \frac{1}{2}{r}_e^f\circ q_e=q_e+\epsilon \frac{1}{2}{q}_e\circ r_e^f$ (3)

上式是对偶四元数在平动–转动的基础上得出的姿态对偶四元数公式，其中 $q_e$ 为Leader航天器与Follower航天器间的相对姿态， $r_e^f$ $\left(r_e^f=r_l-r_f\right)$ 领航航天器Leader相对于追踪航天器Follower在领航航天器本体坐标系下的矢量变化。依据式(3)对于时间的微分方程可得一般的航天器对偶四元数运动微分方程。

$\stackrel{\dot{}}{\hat{q}}=\frac{1}{2}{\hat{\omega }}_e^f\circ {\hat{q}}_e=\frac{1}{2}{\hat{q}}_e\circ {\hat{\omega }}_e^l$ (4)

其中对于特殊的单位对偶四元数有 ${\hat{q}}^{*}\circ \hat{q}=1$ ，对其求导可得对偶四元数转置公式为：

${\stackrel{\dot{}}{\hat{q}}}^{*}=-\frac{1}{2}{\hat{\omega }}_e^l\circ {\hat{q}}^{*}$ (5)

${\omega }_e^l$ 与 ${\omega }_e^f$ 分别为追踪航天器Follower相对于领航航天器Leader的对偶速度旋量在自身坐标系中的矢量，具体矢量公式为

$\{\begin{array}{l}{\hat{\omega }}_e^l={\hat{\omega }}_e^l+\epsilon v_e^l\hfill \\ {\hat{\omega }}_e^f={\hat{\omega }}_e^f+\epsilon v_e^f\hfill \end{array}$ (6)

依据对偶四元数的性质可将式(6)中的对偶速度旋量分解为速度与角速度旋量

${\hat{\omega }}_e^l={\omega }_e^l+\epsilon \left({\stackrel{\dot{}}{r}}_e^f+{\omega }_e^l\times r_e^l\right)={\omega }_e^l+\epsilon \left(q_e^{*}\circ {\stackrel{\dot{}}{r}}_e^f\circ q_e\right)={\omega }_e^l+\epsilon v_e^l$ (7)

上式(7)中的 ${\omega }_e^l$ 为Follower航天器相对于Leader航天器的角速度运动矢量在Leader航天器本体坐标系中的分量； $v_e^l$ 为Follower航天器相对于Leader航天器的角速度运动矢量在Leader航天器本体坐标系中的分量。

2.3. 姿轨耦合动力学方程

根据文献 [9] 可知，可用对偶动量描述刚体航天器的姿态，表达式为

$\hat{H}=M\hat{\omega }=mv+\epsilon J\omega$ (8)

M为表示刚体质量m和转动惯量J的矩阵 $\left[\begin{array}{cc}{0}_{3\times 3}& m{E}_{3\times 3}\\ J& 0_{3\times 3}\end{array}\right]$ ，定义 $\hat{M}$ 为

$\hat{M}=m\frac{\text{d}}{\text{d}t}{I}_{3\times 3}+\epsilon J$ (9)

由文献 [10] 可得对偶形式的刚体航天器牛顿欧拉动力学方程为

$\hat{F}=\frac{\text{d}}{\text{d}t}\hat{H}=M\stackrel{\dot{}}{\hat{\omega }}+\hat{\omega }\times M\hat{\omega }$ (10)

定义 $\hat{F}=f+\epsilon \tau$ ，可知是作用于Follower航天器的力与力矩分别为f与 $\tau$ ，其中 $\stackrel{\dot{}}{\hat{\omega }}$ 是对偶速度旋量为 $\hat{\omega }$ 在航天器质心本体坐标的导数。Follower航天器相对于Leader航天器的速度旋量在Leader航天器坐标可表示为

${\hat{\omega }}_e^l={\hat{\omega }}_l^l-q_e^{\ast }\circ {\hat{\omega }}_f^f\circ q_e$ (11)

${\hat{\omega }}_l^l$ 与 ${\hat{\omega }}_f^f$ 分别为Leader与Follower航天器在自身本体坐标下的分量。对式(11)两端求导，将式(4)和(5)代入求导后的公式可求得初步的运动学方程为

$\begin{array}{c}{\stackrel{\dot{}}{\hat{\omega }}}_e^l={\stackrel{\dot{}}{\hat{\omega }}}_e^l-{\hat{q}}_e^{*}\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e-{\stackrel{\dot{}}{\hat{q}}}_e\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e-{\hat{q}}_e^l\circ {\hat{\omega }}_f^f\circ {\stackrel{\dot{}}{\hat{q}}}_e\\ ={\stackrel{\dot{}}{\hat{\omega }}}_l^l-{\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e+{\hat{\omega }}_e^l\times {\hat{\omega }}_f^f\end{array}$ (12)

由欧拉动力学方程与式(12)得

$\begin{array}{c}M{\stackrel{\dot{}}{\hat{\omega }}}_e^l=M{\stackrel{\dot{}}{\hat{\omega }}}_e^l-M\left({\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e\right)+M\left({\hat{\omega }}_e^l\times {\hat{\omega }}_f^f\right)\\ =\hat{F}-{\hat{\omega }}_l^l\times M{\hat{\omega }}_e^l-M\left({\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e\right)+M\left({\hat{\omega }}_e^l\times {\hat{\omega }}_f^f\right)\end{array}$ (13)

对上式整理得

${\stackrel{\dot{}}{\hat{\omega }}}_e^l=M^{-1}\hat{F}-M^{-1}\left({\hat{\omega }}_l^l\times M{\hat{\omega }}_l^l\right)-{\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e+{\hat{\omega }}_e^l\times \left({\hat{q}}_e^{*}\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e\right)$ (14)

由式(11)可知

${\hat{\omega }}_l^l={\hat{\omega }}_e^l+{\hat{q}}^{*}\circ {\hat{\omega }}_f^f\circ \hat{q}$ (15)

将上式代入式(14)可得

$\begin{array}{c}{\stackrel{\dot{}}{\hat{\omega }}}_e^l=-M^{-1}\left(\left({\hat{\omega }}_e^l+{\hat{q}}^{*}\circ {\hat{\omega }}_f^f\circ \hat{q}\right)\times M\left({\hat{\omega }}_e^l+{\hat{q}}^{*}\circ {\hat{\omega }}_f^f\circ \hat{q}\right)\right)\\ +M^{-1}\hat{F}-{\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e+{\hat{\omega }}_e^l\times \left({\hat{\omega }}_e^l+{\hat{q}}_e^{*}\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e\right)\end{array}$ (16)

上式(16)去除了领航航天器在本体坐标下的速度分量，即所求得追踪航天器相对于领航航天器的相对一体化动力学控制。

2.4. 相对姿轨耦合影响分析

运用对偶四元数的基本运算法则 [11] ，可得

$M^{-1}\hat{F}=\left[\begin{array}{cc}{0}_{3\times 3}& J^{-1}\\ \frac{1}{m}{E}_{3\times 3}& 0_{3\times 3}\end{array}\right]\left[\begin{array}{c}f\\ \tau \end{array}\right]=\left[\begin{array}{c}{J}^{-1}\tau \\ \frac{1}{m}f\end{array}\right]$ (17)

$\begin{array}{c}-M^{-1}\left({\hat{\omega }}_l^l+M{\hat{\omega }}_l^l\right)=-\left[\begin{array}{cc}{0}_{3\times 3}& J^{-1}\\ \frac{1}{m}{E}_{3\times 3}& 0_{3\times 3}\end{array}\right]\left\{\left[\begin{array}{cc}{\omega }_l^l& 0_{3\times 3}\\ {\nu }_l^l& {\omega }_l^l\end{array}\right]\left(\left[\begin{array}{cc}{0}_{3\times 3}& m{E}_{3\times 3}\\ J& 0_{3\times 3}\end{array}\right]\left[\begin{array}{c}{\omega }_l^l\\ {\nu }_l^l\end{array}\right]\right)\right\}\\ =-\left[\begin{array}{c}{J}^{-1}\left({\omega }_l^l\times \left(J{\omega }_l^l\right)\right)\\ {\omega }_l^l\times {\nu }_l^l\end{array}\right]\end{array}$ (18)

$-{\hat{q}}_e^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e=-\left[\begin{array}{c}{\stackrel{\dot{}}{\omega }}_l^l\\ {\stackrel{\dot{}}{v}}_l^l\end{array}\right]$ (19)

${\hat{\omega }}_e^l\times \left({\hat{\omega }}_e^l+{\hat{q}}_e^{*}\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e\right)=\left[\begin{array}{cc}{\omega }_e^l& 0_{3\times 3}\\ v_e^l& {\omega }_e^l\end{array}\right]\left[\begin{array}{c}{\omega }_l^l\\ v_l^l\end{array}\right]=\left[\begin{array}{c}{\omega }_e^l\times {\omega }_l^l\\ v_e^l\times {\omega }_l^l+{\omega }_e^l\times v_l^l\end{array}\right]$ (20)

将分解得到的对偶部与实数部代入式(16)可得航天器位姿一体化控制模型为

${\stackrel{\dot{}}{\omega }}_e^l=-J^{-1}\left[\left({\omega }_e^l+C_e{\omega }_f^f\right)\times J\left({\omega }_e^l+C_e{\omega }_f^f\right)\right]-C_e{\stackrel{\dot{}}{\omega }}_f^f+{\omega }_e^l\times C_e{\omega }_f^f+J^{-1}\tau$ (21)

其中 $C_e$ 是替换了四元数坐标变换的方向余弦矩阵 [12] 。式(21)描述的是航天器相对姿轨耦合动力学模型的实部。

$\begin{array}{c}{\stackrel{\dot{}}{\nu }}_e^l=-2C_e{\omega }_f^f\times v_e^l-C_e{\omega }_f^f\times \left(C_e{\omega }_f^f\times r_e^l\right)-C_e{\stackrel{\dot{}}{\omega }}_l^l\times r_e^l-{\omega }_e^f\times v_e^l\\ -{\omega }_e^f\left({\omega }_e^f\times r_e^l\right)-2C_e{\omega }_f^f\times \left({\omega }_f^f\times r_e^l\right)+\frac{f}{m}\end{array}$ (22)

式(22)为航天器姿轨耦合动力学模型中的虚部，描述的是航天器相对轨道控制。

2.5. 相对姿轨耦合控制

依据前式(5)和(16)可得姿轨耦合方程

$\{\begin{array}{l}{\stackrel{\dot{}}{\hat{q}}}_e=\frac{1}{2}{\hat{q}}_e\circ {\hat{\omega }}_e^l\\ M{\stackrel{\dot{}}{\omega }}_e^l=-\left({\hat{\omega }}_e^l+{\hat{q}}^{*}\circ {\hat{\omega }}_f^f\circ \hat{q}\right)\times \left({\hat{\omega }}_e^l+{\hat{q}}^{*}\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ \hat{q}\right)\\ -M^{-1}\left({\hat{q}}^{*}{}_e\circ {\stackrel{\dot{}}{\hat{\omega }}}_f^f\circ {\hat{q}}_e-{\hat{\omega }}_e^l\times \left({\hat{q}}^{*}{}_e\circ {\hat{\omega }}_f^f\circ {\hat{q}}_e\right)\right)+\hat{F}\\ =\hat{h}+\hat{F}\end{array}$ (23)

上式中的 $\hat{h}$ 的定义式为 $\hat{h}=h_f+\epsilon h_{\tau }$ ， $h_f$ 与 $h_{\tau }$ 分别是实部和对偶部。在整个追踪环境中，要求在一定的时间内达到航天器交会条件，即必须控制Follower航天器与Leader航天器相对姿态保持不变，再利用Follower航天器的动力机构推动前行，缩短与领航航天器间的距离。本文的控制目标是在一定时间内(500 s)使 ${\hat{q}}_e\to \hat{1}$ ，此时的相对姿轨收敛为单位对偶四元数，同时也要求轨道参数也趋于稳定，即收敛于0。由上式(22)可以看出角速度与轨道存在耦合项。现设计PD控制如下：

$\hat{F}=-2{\hat{k}}_q\ln \left({\hat{q}}_e\right)-{\hat{k}}_d{\hat{\omega }}_e^l-\hat{h}$ (24)

上式(24)中的 $\ln \left({\hat{q}}_e\right)$ 依据参考文献 [13] 可得：

$\ln \left({\hat{q}}_e\right)=\ln \left(q+\epsilon \frac{1}{2}r\circ q\right)=\frac{1}{2}\left(\phi n+\epsilon r\right)$ (25)

上式(25)得右项式中得 $\phi$ 趋于0时，可得 $\frac{1}{2}\left(\phi n+\epsilon r\right)\approx q+\epsilon \frac{1}{2}r$ ， $\phi$ 是转角，n是平均轨道角速度，r是轨道半轴。定义

${\hat{D}}_q=q+\epsilon \frac{1}{2}r$ (26)

本文重点在于对偶控制参数的改变，改变了以往固定控制参数，添加了自调整函数 $\left(1+a-{\text{e}}^{-bt}\right)$ ，具体为 ${\hat{k}}_q=k_r+\epsilon k_s$ ， ${\hat{k}}_d=k_v\left(1+a-{\text{e}}^{-bt}\right)+\epsilon k_w\left(1+a-{\text{e}}^{-bt}\right)$ ，自调整函数中a与b为正数常量，将 ${\hat{k}}_q$ ， ${\hat{k}}_d$ 与自调整函数代入式(25)可得到调整后控制器的对偶部与实部。

$f=-\frac{1}{2}{k}_r{r}_e^l-k_v\left(1+a-{\text{e}}^{-bt}\right)\left(v_e^l+{\omega }_e^l\times r_e^l\right)-h_{\tau }$ (27)

$\tau =-k_s{q}_e-k_{\omega }\left(1+a-{\text{e}}^{-bt}\right){\omega }_e^l-h_f$ (28)

下面根据Lyapunov函数证明上述添加了自调整后控制律的稳定性，Lyapunov函数为

$V\left({\hat{q}}_e,{\hat{\omega }}_e^l\right)={\left({\hat{k}}_q\left({\hat{q}}_e-\hat{1}\right)\right)}^{\text{T}}\circ \left({\hat{q}}_e-\hat{1}\right)+\frac{1}{2}{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left(M{\hat{\omega }}_e^l\right)$ (29)

对公式(29)求导，可得

$\begin{array}{c}\stackrel{\dot{}}{V}\left({\hat{q}}_e,{\hat{\omega }}_e^l\right)=2{\left({\hat{k}}_q\left({\hat{q}}_e-\hat{1}\right)\right)}^{\text{T}}\circ {\stackrel{\dot{}}{\hat{q}}}_e+\frac{1}{2}{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left(M{\stackrel{\dot{}}{\hat{\omega }}}_e^l\right)\\ ={\left({\hat{k}}_q\left({\hat{q}}_e-\hat{1}\right)\right)}^{\text{T}}\circ \left({\hat{q}}_e\circ {\hat{\omega }}_e^l\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\\ ={\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{q}}_e^{*}\circ \left({\hat{k}}_q\left({\hat{q}}_e-\hat{1}\right)\right)\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\\ ={\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left(\left(q_e^{*}+\epsilon \frac{1}{2}{\left(q_e\circ r_e^f\right)}^{*}\right)\circ \left(\frac{1}{2}{k}_r\left(q_e\circ r_e^l\right)+\epsilon k_s\left(q_e-1\right)\right)\right)\\ -{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\end{array}$

$\begin{array}{c}=\frac{1}{2}{k}_r{r}_e^l+\epsilon k_s{q}_e-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\\ ={\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_q{\hat{D}}_q\right)-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\\ =-{\left({\hat{\omega }}_e^l\right)}^{\text{T}}\circ \left({\hat{k}}_d\circ {\hat{\omega }}_e^l\right)\le 0\end{array}$ (30)

上式中可知可得上式求导小于零。当 ${\hat{\omega }}_e^l=0$ 时， $\stackrel{\dot{}}{V}\left({\hat{q}}_e,{\hat{\omega }}_e^l\right)=0$ ，当 $\left({\hat{q}}_e,{\hat{\omega }}_e^l\right)\to \infty$ 时， $\stackrel{\dot{}}{V}\left({\hat{q}}_e,{\hat{\omega }}_e^l\right)\to \infty$ 。故整个系统是渐近稳定的。

3. 仿真实验

在航天器间追踪过程中的最后交会阶段验证了本文所提自调整PD跟踪控制的可行性。航天器交会对接是指将Leader航天器在其本体坐标系下的姿态与轨迹作为Follower航天器的追踪目标。已知航天器整体质量为500 kg，Flower航天器与Leader航天器的相对姿态与位置定量 $q_e:{\left[0.6154-0.55690.5215-0.2560\right]}^{\text{T}}$ ， $r_e^l:{\left[220-100100\right]}^{\text{T}}$ ，表示Flower航天器与Leader航天器在准备交会前，要达到上述相对初始位置与姿态。航天器的转动惯量为 $J=diag\left(22,20,23\right)$ ，设置追踪航天器承受的最大的控制力范围为[−50, 50] N和控制力矩范围为[−1, 1] N * m。在整个航天器追踪仿真模拟中，要求航天器交会前的初始相对速度与角速度控制要求为 $v_e^l:{\left[0.250.250.25\right]}^{\text{T}}$ m∙s⁻¹， ${\omega }_e^l:{\left[0.0020.0010.002\right]}^{\text{T}}$ rad∙s⁻¹，自调整函数中 $a=0.1$ ， $b=0.01$ ，具体控制参数设置为 $k_r=1.6$ ， $k_s=1.5$ ， $k_v=6$ ， $k_w=15$ 。仿真结果如下图2~7所示。

由图2，图3可以看出追踪条件下的相对角速度与相对姿态角的变化，从图中可以看出在100~150 s的时间内两图都有较大的震颤，在150 s后两图就趋于稳定状态，即是实现航天器间相对姿态角与相对角速度稳定。

图4，图5可以看出追踪条件下的相对速度与相对位置的变化曲线，由于给定的初始位置较大，相对速度与位置曲线还是在380 s后就趋于稳定了，相对应的控制精度也达到了0.548 * 10⁻³ m和0.836 * 10⁻⁴ m/s。图6，图7与图8，图9的对比，可以看出添加了自调整函数后的显著效果，明显可以看出添加了自调整函数的控制力与控制力矩的震颤得到很大的减缓，控制力曲线趋于稳定的速度比未加自调整函数的曲线速度更快，控制力矩曲线以更加平缓的速度趋于稳定，也验证了本文所添加自调整函数的可行性，满足了航天器交会任务的需求。

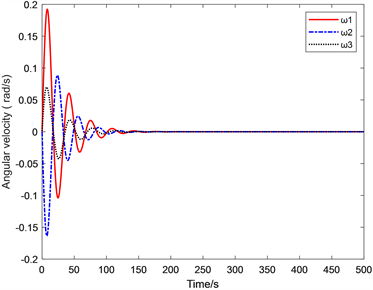
Figure 2. Spacecraft relative angular velocity

图2. 航天器相对角速度

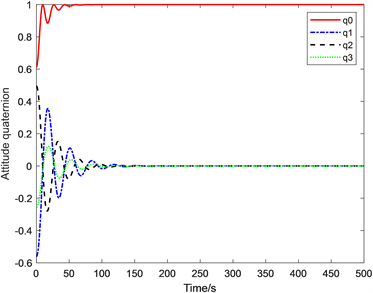
Figure 3. Spacecraft relative attitude angle

图3. 航天器相对姿态角

Figure 4. Spacecraft relative velocity

图4. 航天器相对速度

Figure 5. Spacecraft relative position

图5. 航天器相对位置

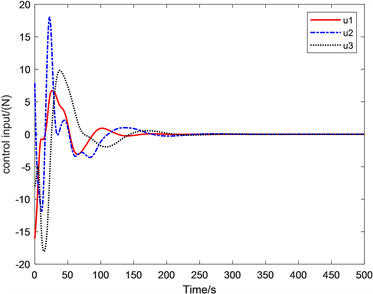
Figure 6. Curve of self adjusting control torque

图6. 自调整控制力矩曲线图

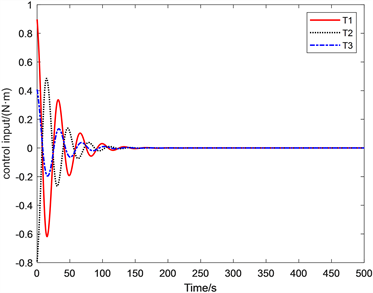
Figure 7. Curve of self adjusting control force

图7. 自调整控制力曲线图

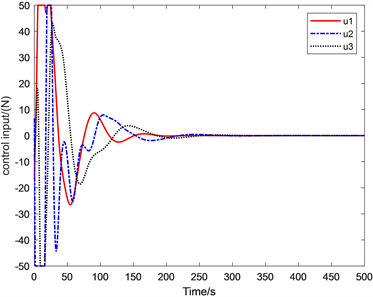
Figure 8. Curve of no self adjusting control torque

图8. 无自调整控制力矩曲线图

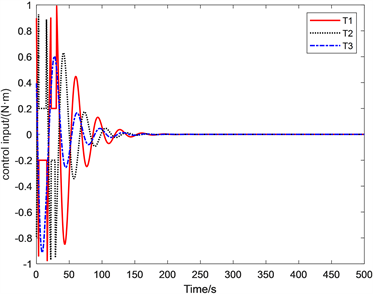
Figure 9. Curve of no self adjusting control force

图9. 无自调整控制力曲线图

4. 结论

本文设计了一种关于对偶四元数的航天器姿轨耦合自调整控制方法，将以往K_d固定不变量设置为自调整量，为减小航天器追踪过程的震颤，并利用Lyapunov函数证明了加入自调整后的控制系统的稳定性。实验结果也充分证明了在自调整条件下的控制力与控制力矩变化曲线的饱和度减小，可为追踪航天工程任务提供参考。

基金项目

国家自然科学基金(61973167)；教育部产学合作协同育人项目(22097110113736)；盐城工学院校级科研项目(xjr2020041)。

NOTES

^*通讯作者。