阈值策略下一类Lotka-Volterra Filippov型植物传染病模型的全局动力学

Global Dynamics of a Lotka-Volterra Filippov-Type Plant Infectious Disease Model under Threshold Strategy

摘要: 本文研究了阈值策略下一类Lotka-Volterra Filippov型植物传染病模型的全局动力学，当感染植株的数量和易感植株的数量比例小于数值k时，不采取措施，传染病最终会衍变成病；当感染植株的数量和易感植株的数量比例大于数值k时，采取等比例种植易感植株和移除感染植株的方式控制传染病传播。通过不同参数的取值，得到四种情形，分别分析了这四种情形下系统的全局动力学行为，得到四种结果。

Abstract: In this paper, the global dynamics of the Lotka-Volterra Filippov plant infectious disease model un-der the threshold strategy are studied, and when the ratio of the number of infected plants and the number of susceptible plants is less than the value k, if no measures are taken, the infectious dis-ease will eventually evolve into a disease. When the ratio of the number of infected plants to the number of susceptible plants is greater than the value k, the spread of infectious diseases is con-trolled by planting susceptible plants and removing infected plants in equal proportions. Through the values of different parameters, four situations are obtained, and the global dynamic behavior of the system in these four situations is analyzed respectively, and four results are obtained.

1. 模型介绍

本文研究了阈值策略下一类特殊的Lotka-Volterra Filippov型植物传染病模型 [1] [2] ，其中被移除的感染植物的数量等于重新种植的易感植物的数量，具体模型为

$\{\begin{array}{l}\frac{\text{d}S\left(t\right)}{\text{d}t}=A-\beta S\left(t\right)I\left(t\right)-{\eta }_{1}S\left(t\right)+v\varphi \left(S,I\right)I\left(t\right),\\ \frac{\text{d}I\left(t\right)}{\text{d}t}=\beta S\left(t\right)I\left(t\right)-{\eta }_{2}I\left(t\right)-v\varphi \left(S,I\right)I\left(t\right)\end{array}$ (1.1)

其中 $S\left(t\right)$ 和 $I\left(t\right)$ 分别表示t时刻易感植株和感染植株的数量；A表示易感植株的种植数量，为一常数； $\beta >0$ 表示传染病感染率； ${\eta }_1>0$ 和 ${\eta }_2>0$ 分别表示易感植株和感染植株的自然死亡率； $v>0$ 去除率； $\varphi \left(S,I\right)$ 是控制函数，具体表达式为

$\varphi \left(S,I\right)=\{\begin{array}{l}0,\frac{I}{S}<k,\\ 1,\frac{I}{S}>k,\end{array}$

其中 $k\ge 0$ 表示感染植株的经济阈值与易感比率。当易感植株和感染植株的比例小于k时，不需要采取任何控制措施。一旦比例超过经济阈值k，就立刻采取措施移除感染植株同时补种同样数量的易感植株，以控制病虫害。在本文中，我们假设 ${\eta }_1<{\eta }_2$ 意味着易感植物的自然死亡率小于感染植物的自然死亡率。

分界线记为

$\Sigma =\left\{\left(S,I\right)\in R_{+}^2|I=Sk\right\}$

它把系统(1.1)划分为两个光滑的区域

$G_1=\left\{\left(S,I\right)\in R_{+}^2|I<Sk\right\},G_2=\left\{\left(S,I\right)\in R_{+}^2|I>Sk\right\}$

其中 $R_{+}^2=\left\{\left(S,I\right)|S>0,I>0\right\}$ 。因此在区域 $G_1$ 上模型(1.1)变为

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=A-\beta SI-{\eta }_{1}S,\\ \frac{\text{d}I}{\text{d}t}=\beta SI-{\eta }_{2}I,\end{array}I<Sk$ (1.2)

在区域 $G_2$ 上模型(1.1)变为

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=A-\beta SI-{\eta }_{1}S+vI,\\ \frac{\text{d}I}{\text{d}t}=\beta SI-{\eta }_{2}I-vI,\end{array}I>Sk,$ (1.3)

2. 预备知识

由于(1.1)右端的不连续性，在本文中，定义了一个具有初始条件的(1.1)的解。设 $\overline{co}\left[\varphi \left(S,I\right)\right]$ 为 $\varphi \left(S^{-},I^{-}\right)$ 凸闭包，则 $\overline{co}\left[\varphi \left(S,I\right)\right]=\left[\varphi \left(S^{-},I^{-}\right),\varphi \left(S^{+},I^{+}\right)\right]$ ，其中 $\varphi \left(S^{-},I^{-}\right)$ 和 $\varphi \left(S^{+},I^{+}\right)$ 分别表示 $\varphi$ 在的左右极限 [3] 。

定义 2.1 [4] . 若向量函数 $\left(S\left(t\right),I\left(t\right)\right)$ 在 $\left[0,T\right)$ ， $T\in \left(0,+\infty \right)$ 的任何子区间 $\left[t_1,t_2\right]$ 上绝对连续，满足初值条件 $S\left(0\right)=S_0>0$ 且 $I\left(0\right)=I_0>0$ ，并且存在可测函数 $\gamma \left(t\right):\left[0,T\right)\to R$ ，使得对几乎所有的 $t\in \left[0,T\right)$ 有 $\gamma \left(t\right)\in \overline{co}\left[\varphi \left(S\left(t\right),I\left(t\right)\right)\right]$ 和

$\{\begin{array}{l}\frac{\text{d}S\left(t\right)}{\text{d}t}=A-\beta S\left(t\right)I\left(t\right)-{\eta }_{1}S\left(t\right)+v\gamma \left(t\right)I\left(t\right),\\ \frac{\text{d}I\left(t\right)}{\text{d}t}=\beta S\left(t\right)I\left(t\right)-{\eta }_{2}I\left(t\right)-v\gamma \left(t\right)I\left(t\right),\end{array}$

则在 $\left[0,T\right)$ ， $T\in \left(0,+\infty \right)$ 上的向量函数 $\left(S\left(t\right),I\left(t\right)\right)$ 是系统(1.1)带初值 $S\left(0\right)=S_0$ ， $I\left(0\right)=I_0$ 的解。

引理2.1对系统(1.1)在 $R_{+}^2$ 中任意的初值条件下，集合 $\Omega =\left\{\left(S,I\right)\in R_{+}^2:S+I\le \frac{A}{\lambda }\right\}$ 是一个正不变吸引集，其中 $\lambda =\min \left\{{\eta }_1,{\eta }_2\right\}$ 。

证明由(1.1)可知

${\left(S+I\right)}^{\prime }=A-{\eta }_{1}S-{\eta }_{2}I\le A-\lambda \left(S+I\right)$

两边积分得

$S\left(t\right)+I\left(t\right)\le \frac{A}{\lambda }+\left(S_0+I_0-\frac{A}{\lambda }\right){\text{e}}^{-\lambda t}$

若 $S_0+I_0\le \frac{A}{\lambda }$ ，则 $S\left(t\right)+I\left(t\right)\le \frac{A}{\lambda }$ ，即 $\Omega$ 为正不变集。

下面证明 $\Omega$ 为吸引集。假设 $S\left(t\right)+I\left(t\right)>\frac{A}{\lambda }$ ，则 $\lambda \left(S\left(t\right)+I\left(t\right)\right)>A$ ，因为

$S\left(t\right)+I\left(t\right)\le \frac{A}{\lambda }+\left(S_0+I_0-\frac{A}{\lambda }\right){\text{e}}^{-\lambda t}$

所以 $\underset{t\to \infty }{\lim }\left(S\left(t\right)+I\left(t\right)\right)\le \frac{A}{\lambda }$ ，说明 $\Omega$ 为吸引集。

3. 子系统及滑模域上的动力学

在本节中，讨论系统(1.1)的子系统和滑模区域上的动力学行为。

3.1. 子系统上的动力学

这一部分，讨论系统(1.1)的子系统上(1.2)，(1.3)的动力学行为。

对于子系统(1.2)，基本再生素 $R_1=\frac{A\beta }{{\eta }_1{\eta }_2}$ 。它有两个平衡点，无病平衡点(DFE)和地方病平衡点(EE)分别由下式给出

$E_0^{-}=\left(\frac{A}{{\eta }_1},0\right),E_1=\left(S_1,I_1\right)=\left(\frac{{\eta }_2}{\beta },\frac{A\beta -{\eta }_1{\eta }_2}{{\eta }_2\beta }\right),$

定理3.1 对于子系统(1.2)，若 $R_1<1$ ，则无病平衡点 $E_0^{-}$ 是全局渐近稳定的。若 $R_1>1$ ，则地方病平衡点 $E_1$ 是全局渐近稳定的。

证明 若 $R_1<1$ ，把系统(1.2)改写成

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=-{\eta }_1\left(S-\frac{A}{{\eta }_1}\right)\\ \frac{\text{d}I}{\text{d}t}=0\end{array}$ (3.1)

考虑Lyapunov函数

$V_0^{-}\left(S,I\right)=\frac{1}{2}{\left(S-\frac{A}{{\eta }_1}\right)}^{\text{2}}+\frac{A}{{\eta }_1}I$

沿系统(3.1)对 $V_0^{-}\left(S,I\right)$ 求导可得

$\frac{\text{d}}{\text{d}t}{V}_0^{-}\left(S,I\right)=-{\eta }_1{\left(S-\frac{A}{{\eta }_1}\right)}^{\text{2}}\le 0$

由LaSalle不变原理，可得 $E_0^{-}$ 是全局渐近稳定的。证毕。

若 $R_1>1$ 时，把系统(1.2)改写成如下形式

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\left(S-S_1\right)-\beta \left(S-S_1\right)I-{\eta }_2\left(I-I_1\right)\\ \frac{\text{d}I}{\text{d}t}=\beta \left(S-S_1\right)I\end{array}$ (3.2)

考虑Lyapunov函数

$V_1\left(S,I\right)=\frac{1}{2}{\left(S-S_1\right)}^2+\frac{{\eta }_2}{\beta }\left(I-I_1-I_1\ln \frac{I}{I_1}\right)$

沿系统(3.2)对 $V_1\left(S,I\right)$ 求导可得

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{V}_1\left(S,I\right)=-{\eta }_1{\left(S-S_1\right)}^{\text{2}}-\beta {\left(S-S_1\right)}^{\text{2}}I-\beta \left(S-S_1\right)\left(I-I_1\right)+\beta \left(S-S_1\right)\left(I-I_1\right)\\ =-\left({\eta }_1+\beta U\right){\left(S-S_1\right)}^{\text{2}}\le 0\end{array}$

由LaSalle不变原理，可得 $E_1$ 是全局渐近稳定的。证毕。

对于子系统 (1.3), 基本再生素 $R_{\text{2}}=\frac{A\beta }{\left({\eta }_2+v\right){\eta }_1}$ ，它有两个平衡点，地方病平衡点和无病平衡点为

$E_0^{+}=\left(\frac{A}{{\eta }_1},0\right),E_2=\left(S_2,I_2\right)=\left(\frac{{\eta }_2+v}{\beta },\frac{A\beta -{\eta }_1\left({\eta }_2+v\right)}{{\eta }_2\beta }\right),$

定理3.2 对于子系统(1.3)，若 $R_2<1$ 且 ${\eta }_1\le \frac{4\left(1-R_2\right)A\beta \left({\eta }_2+v\right)}{v^2}$ ，则无病平衡点 $E_0^{+}$ 是全局渐近稳定的。若 $R_2>1$ ，则地方病平衡点 $E_2$ 是全局渐近稳定的。

证明当 $R_2<1$ 时，将系统 (1.3) 改写成如下形式

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=-{\eta }_1\left(S-\frac{A}{{\eta }_1}\right)-\beta SI+vI,\\ \frac{\text{d}I}{\text{d}t}=\beta SI-{\eta }_{2}I-vI,\end{array}$ (3.3)

考虑Lyapunov函数

$V_0^{+}\left(S,I\right)=\frac{1}{2}{\left(S-\frac{A}{{\eta }_1}\right)}^{\text{2}}+\frac{A}{{\eta }_1}I.$

沿着系统(3.3)对函数 $V_0^{+}\left(S,I\right)$ 求导

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{V}_0^{-}\left(S\left(t\right),I\left(t\right)\right)=-{\eta }_1{\left(S-\frac{A}{{\eta }_1}\right)}^2-\beta S^{2}I+\frac{A}{{\eta }_1}\beta SI+vSI-\frac{A}{{\eta }_1}vI+\frac{A}{{\eta }_1}\left(\beta SI-{\eta }_{2}I-vI\right)\\ =-{\eta }_1{\left(S-\frac{A}{{\eta }_1}\right)}^2-\beta I{\left(S-\left(\frac{A}{{\eta }_1}+\frac{v}{2\beta }\right)\right)}^2+g\left(I\right)\\ \le 0\end{array}$

其中

$g\left(I\right)=\frac{A\left({\eta }_2+v\right)\left(\frac{A\beta }{{\eta }_1\left({\eta }_2+v\right)}-1+\frac{{\eta }_1{v}^2}{4A\beta \left({\eta }_2+v\right)}\right)}{\beta {\eta }_1}I.$

当 ${\eta }_1\le \frac{4\left(1-R_2\right)A\beta \left({\eta }_2+v\right)}{v^2}$ 时，有 $g\left(I\right)\le 0$ 。有Lasalle不变原理，可得 $E_0^{+}$ 是全局渐近稳定的。

当 $R_2>1$ 时，将系统(1.3)改写成如下形式

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=-{\eta }_1\left(S-S_2\right)-\beta \left(S-S_2\right)I-{\eta }_2\left(I-I_2\right),\\ \frac{\text{d}I}{\text{d}t}=\beta \left(S-S_2\right)I,\end{array}$ (3.4)

考虑Lyapunov函数

$V_2\left(S,I\right)=\frac{1}{2}{\left(S-S_2\right)}^2+\frac{{\eta }_2}{\beta }\left(I-I_2-I_2\ln \frac{I}{I_2}\right).$

沿着系统(3.4)对函数 $V_2\left(S,I\right)$ 求导

$\begin{array}{c}\frac{\text{d}{V}_2\left(S,I\right)}{\text{d}t}=-{\eta }_1{\left(S-S_2\right)}^2-\beta {\left(S-S_2\right)}^{2}I-{\eta }_2\left(S-S_2\right)\left(I-I_2\right)+{\eta }_2\left(S-S_2\right)\left(I-I_2\right)\\ =-\left({\eta }_1+\beta I\right){\left(S-S_2\right)}^2\le 0.\end{array}$

根据Lasalle不变原理，得到 $E_1$ 是全局渐近稳定的。

3.2. 滑模域上的动力学

这一部分，分析系统(1.1)在滑模域上的动力学行为。设 $H\left(S,I\right)=I-Sk$ ，有

$\nabla H=\left(\frac{\partial H}{\partial S},\frac{\partial H}{\partial I}\right)=\left(-k,1\right).$

选取向量 $n=\left(-k,1\right)$ 作为分界线 $\Sigma$ 的法向量。为了方便求滑模域 $\Sigma$ 上的切点，定义如下函数

$g_1\left(S\right)=\langle \nabla H,F_1\left(S,kS\right)\rangle =k\left[\beta \left(k+1\right)S^2+\left({\eta }_1-{\eta }_2\right)S-A\right]$

和

$g_2\left(S\right)=\langle \nabla H,F_2\left(S,kS\right)\rangle =k\left[\beta \left(k+1\right)S^2+\left({\eta }_1-{\eta }_2-v\left(1+k\right)\right)S-A\right]$

当 $g_1\left(S\right)>0$ ， $g_2\left(S\right)<0$ 时，可求得滑模域 ${\Sigma }_1$ 为

${\Sigma }_1=\left\{\left(S,I\right)\in R_{+}^2|S_T^1<S<S_T^2,I=kS\right\}$

其中

$S_T^1=\frac{-\left({\eta }_1-{\eta }_2\right)+\sqrt{{\left({\eta }_1-{\eta }_2\right)}^2+4A\left(1+k\right)\beta }}{2\left(1+k\right)\beta }$

和

$S_T^2=\frac{-\left[{\eta }_1-{\eta }_2-v\left(1+k\right)\right]+\sqrt{{\left[{\eta }_1-{\eta }_2-v\left(1+k\right)\right]}^2+4A\left(1+k\right)\beta }}{2\left(1+k\right)\beta }.$

根据Fillippov凸方法，容易得到滑模方程

$\frac{\text{d}S}{\text{d}t}=\frac{1}{1+k}f\left(S\right),I=kS$

其中 $f\left(S\right)=A-\left({\eta }_1+{\eta }_{2}k\right)S$ ，求得 $f\left(S\right)$ 的零点为 $S_p=\frac{A}{{\eta }_1+{\eta }_{2}k}$ 。

此外，系统(1.1)的唯一伪平衡 $E_p=\left(S_p,k{S}_p\right)$ 存在的充要条件为 $S_T^1<S_p<S_T^2$ 。为了方便判断伪平衡点 $E_p$ 是否存在，给出如下引理

引理 3.1若 ${\eta }_1<{\eta }_2$ ，则下面断言成立：

(i) $\text{sign}\left(S_p-S_T^1\right)=\text{sign}\left(A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2\right)$ ；

(ii) $\text{sign}\left(S_p-S_T^2\right)=\text{sign}\left(A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k\right)$ 其中 $\text{sign}(\cdot )$ 为符号函数

$\text{sign}\left(x\right)=\{\begin{array}{l}1,x>0,\\ 0,x=0,\\ -1,x<0.\end{array}$

证明 (i) 不失一般性，假设 $S_T^1>S_p$ ，下证 $S_T^1>S_p$ 等价于 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 。因为 $f\left(S_p\right)=0$ 以及 $f\left(S\right)$ 的性质，可得 $S_T^1>S_p$ 等价于 $f\left(S_T^1\right)<0$ ，即

$f\left(S_T^1\right)=-\left({\eta }_1+{\eta }_{2}k\right)\left(S_T^1-\frac{A}{{\eta }_1+{\eta }_{2}k}\right)<0,$

可得 $f\left(S_T^1\right)<0$ 当且仅当 $S_T^1>\frac{A}{{\eta }_1+{\eta }_{2}k}$ 。由函数 $g_1\left(S\right)$ 的性质知 $S_T^1>\frac{A}{{\eta }_1+{\eta }_{2}k}$ 等价于

$g_1\left(\frac{A}{{\eta }_1+{\eta }_{2}k}\right)=\frac{Ak\left(1+k\right)}{{\left({\eta }_1+{\eta }_{2}k\right)}^2}\left(A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2\right)<0.$

可得， $S_T^1>S_p$ 当且仅当 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 。

(ii)的证明与(i)的证明类似，这里不再给出证明。证毕。

4. 系统的全局动力学

这一节考虑系统(1.1)的全局动力学行为。首先给出两个引理证明系统(1.1)不在极限环。

引理4.1 系统(1.1)不存在滑模极限环。

证明不失一般性，考虑 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ 的情形，即 $E_1$ 为实平衡点 $E_2$ 是虚平衡点，在这种情况下，证明系统不可能出现如图1所示的滑模极限环。可以得出，实平衡点 $E_1$ 是局部渐近稳定的，并且吸引集合

${\Omega }_1=\left\{\left(S,I\right)|V_1\left(S,I\right)\le V_1\left(S_T^1,k{S}_T^1\right)\right\}.$

因为 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ ，由引理3.1可得， $S_p<S_T^1<S_T^2$ ，此时滑模域上没有伪平衡点。由 $f\left(S\right)$ 的性质可知，当 $S\in \left(S_T^1,S_T^2\right)$ 时，有 $f\left(S\right)<0$ ，即滑模域上的解轨线沿着滑模向下滑动到达切点 $T_1=\left(S_T^1,k{S}_T^1\right)$ 。由于 $\left(S_T^1,k{S}_T^1\right)\in {\Omega }_1$ ，所以从切点出发的解轨线将收敛到 $E_1$ ，说明 $E_1$ 吸引滑模域

反证法。假设存在如图1所示的滑模极限环 $\Gamma$ ，那么滑模极限环 $\Gamma$ 必须从切点 $T_1=\left(S_T^1,k{S}_T^1\right)$ 出发经过一段时间后到达再次到达滑模域 ${\Sigma }_1$ ，这与 $E_1$ 吸引滑模域矛盾，所以系统(1.1)不存在滑模极限环。

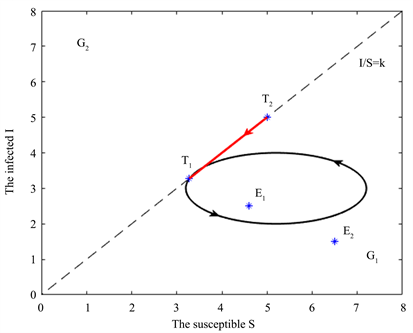
Figure 1. The possible sliding limit cycle if $E_1$ is real and $E_2$ is virtual

图1. 当 $E_1$ 为实平衡点 $E_2$ 为虚平衡，系统可能存在的滑模极限环

引理4.2 系统(1.1)不存在围绕 ${\Sigma }_1$ 的穿越极限环。

证明 反证法。假设存在围绕 ${\Sigma }_1$ 的穿越极限环 $\Gamma$ 如图2所示，设分别 ${\Gamma }_1$ ， ${\Gamma }_2$ 为 $\Gamma$ 在区域 $G_1$ ， $G_2$ 的部分， $P_1$ ， $P_2$ 分别表示为 $\Gamma$ 与 ${\Sigma }_1$ 的交点， $D_1$ ， $D_2$ 分别表示 ${\Gamma }_1$ 和 $P_1{P}_2$ 围成的有界区域以及 ${\Gamma }_2$ 和 $P_1{P}_2$ 围成的有界区域。根据 Bendixson-Dulac判别法，设Dulac 函数为 $B\left(S,I\right)=\frac{1}{SI}$ ，则

${\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle \int {\displaystyle {\int }_{D_i}\frac{\partial \left(B{f}_i^1\right)}{\partial S}+\frac{\partial \left(B{f}_i^2\right)}{\partial I}\text{d}S\text{d}I}}}={\displaystyle \int {\displaystyle {\int }_{D_1}-\frac{A}{S^{2}I}\text{d}S\text{d}I}}+{\displaystyle \int {\displaystyle {\int }_{D_2}-\frac{A}{S^{2}I}-\frac{v}{S^2}\text{d}S\text{d}I}}<0$

其中 $i=1,2$ ，根据格林公式，可得

$\begin{array}{l}{\displaystyle \int {\displaystyle {\int }_{D_1}\frac{\partial \left(B{f}_1^1\right)}{\partial S}+\frac{\partial \left(B{f}_1^2\right)}{\partial I}\text{d}S\text{d}I}}\\ ={\displaystyle {\oint }_{{\Gamma }_1\cup \stackrel{\to }{P_2{P}_1}}B{f}_1^1\text{d}I}-{\displaystyle {\oint }_{{\Gamma }_1\cup \stackrel{\to }{P_2{P}_1}}B{f}_1^2\text{d}S}\\ ={\displaystyle {\int }_{{\Gamma }_1}B{f}_1^1\text{d}I}+{\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}B{f}_1^1\text{d}I}-{\displaystyle {\int }_{{\Gamma }_1}B{f}_1^2\text{d}S}-{\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}B{f}_1^2\text{d}S}\\ ={\displaystyle {\int }_{{\Gamma }_1}B{f}_1^1{f}_1^2\text{d}t}-{\displaystyle {\int }_{{\Gamma }_1}B{f}_1^2{f}_1^1\text{d}t}+{\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}B{f}_1^1\text{d}I}-{\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}B{f}_1^2\text{d}S}\end{array}$

$\begin{array}{l}={\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}\left(kB{f}_1^1-B{f}_1^2\right)\text{d}S}\\ ={\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}\left(\frac{A}{S^2}+\frac{{\eta }_2-{\eta }_1}{S}-\left(k+1\right)\beta \right)\text{d}S}\\ =-A\left(\frac{1}{P_1}-\frac{1}{P_2}\right)-\left(k+1\right)\beta \left(P_1-P_2\right)+\left({\eta }_2-{\eta }_1\right)\ln \left|\frac{P_1}{P_2}\right|\end{array}$

其中，沿着 ${\Gamma }_i\left(i=1,2\right)$ 有 $\text{d}S=f_1^1\text{d}t$ 和 $\text{d}I=f_1^2\text{d}t$ ，沿着 $\Sigma$ 有 $\text{d}I=k\text{d}S$ 。类似的

$\begin{array}{l}{\displaystyle \int {\displaystyle {\int }_{D_2}\frac{\partial \left(B{f}_2^1\right)}{\partial S}+\frac{\partial \left(B{f}_2^2\right)}{\partial I}\text{d}S\text{d}I}}\\ ={\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}\left(kB{f}_2^1-B{f}_2^2\right)\text{d}S}\\ =-A\left(\frac{1}{P_2}-\frac{1}{P_1}\right)-\left(k+1\right)\beta \left(P_2-P_1\right)+\left({\eta }_2-{\eta }_1+\left(k+1\right)v\right)\ln \left|\frac{P_2}{P_1}\right|\end{array}$

因为 $P_1<P_2$ ，所以

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle \int {\displaystyle {\int }_{D_i}\frac{\partial \left(B{f}_i^1\right)}{\partial S}+\frac{\partial \left(B{f}_i^2\right)}{\partial I}\text{d}S\text{d}I}}}\\ ={\displaystyle \int {\displaystyle {\int }_{D_1}\frac{\partial \left(B{f}_1^1\right)}{\partial S}+\frac{\partial \left(B{f}_1^2\right)}{\partial I}\text{d}S\text{d}I}}+{\displaystyle \int {\displaystyle {\int }_{D_2}\frac{\partial \left(B{f}_2^1\right)}{\partial S}+\frac{\partial \left(B{f}_2^2\right)}{\partial I}\text{d}S\text{d}I}}\\ ={\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}\left(kB{f}_1^1-B{f}_1^2\right)\text{d}S}+{\displaystyle {\int }_{\stackrel{\to }{P_2{P}_1}}\left(kB{f}_2^1-B{f}_2^2\right)\text{d}S}\\ =v\left(k+1\right)\ln \left|\frac{P_2}{P_1}\right|>0\end{array}$

矛盾，因此引理4.2可证。

Figure 2. The possible crossing limit cycle

图2. 系统可能存在的穿越极限环

情形1 $R_1\le 1$

定理4.1 当 $R_1\le 1$ 且 ${\eta }_1<\frac{4\left(1-R_1\right)A\beta {\eta }_2}{v^2}$ ，则无病平衡点 $E_0^{-}$ 是全局渐近稳定的。

证明 设 $\left(S\left(t\right),I\left(t\right)\right)$ 是(1.1)满足初值条件 $S\left(0\right)=S_0>0$ ， $I\left(0\right)=I_0>0$ 的解，根据定义2.1，存在一个可测函数 $\gamma \left(t\right)\in \left[0,1\right]$ ，使得对几乎所有的 $t\in \left[0,+\infty \right)$ 都有

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=A-\beta SI-{\eta }_{1}S+v\gamma I,\\ \frac{\text{d}I}{\text{d}t}=\beta SI-{\eta }_{2}I-v\gamma I,\end{array}$ (4.1)

其中

$\{\begin{array}{l}\gamma =0,I<Sk,\\ \gamma =1,I>Sk,\\ \gamma =\left[0,1\right],I=Sk.\end{array}$

设 $g\left(\gamma ,I\right)=\frac{4A^2{\beta }^2+{\gamma }^2{\eta }_1^2{v}^2-4A\beta {\eta }_1{\eta }_2}{4\beta {\eta }_1^2}I$ ，下证 $g\left(\gamma ,I\right)\le 0$ 。当 $I<Sk$ ，此时 $\gamma =0$ ，所以

$g\left(\gamma ,I\right)=\frac{4A\beta {\eta }_1{\eta }_2\left(R_1-1\right)}{4\beta {\eta }_1^2}I\le 0$

当 $I\ge Sk$ 时，此时 $0<\gamma \le 1$ ， $R_1\le 1$ ， ${\eta }_1<\frac{4\left(1-R_1\right)A\beta {\eta }_2}{v^2}$ ，所以t

$g\left(\gamma ,I\right)\le g\left(1,k\right)=\frac{4A^2{\beta }^2+{\eta }_1^2{v}^2-4A\beta {\eta }_1{\eta }_2}{4\beta {\eta }_1^2}k\le 0.$

考虑Lyapunov函数

$V\left(S,I\right)=\frac{1}{2}{\left(S-\frac{A}{{\eta }_1}\right)}^{\text{2}}+\frac{A}{{\eta }_1}I$

函数 $V\left(S,I\right)$ 沿着系统(4.1)求导

$\begin{array}{c}\frac{\text{d}}{\text{d}t}V\left(S\left(t\right),I\left(t\right)\right)=\left(S-\frac{A}{{\eta }_1}\right)\left(A-\beta SI-{\eta }_{1}S+v\gamma I\right)+\frac{A}{{\eta }_1}\left(\beta SI-{\eta }_{2}I-v\gamma I\right)\\ \le \left(S-\frac{A}{{\eta }_1}\right)\left(A-\beta SI-{\eta }_{1}S+v\gamma I\right)+\frac{A}{{\eta }_1}\left(\beta SI-{\eta }_{2}I\right)\\ =-{\eta }_1{\left(S-\frac{A}{{\eta }_1}\right)}^2-\beta I{\left(S-\frac{2A\beta +\gamma {\eta }_{1}v}{2\beta {\eta }_1}\right)}^2+g\left(\gamma ,I\right)\\ \le 0\end{array}$

由Lasalle不变原理，得到 $E_0^{-}$ 是全局渐近稳定的，如图3所示。

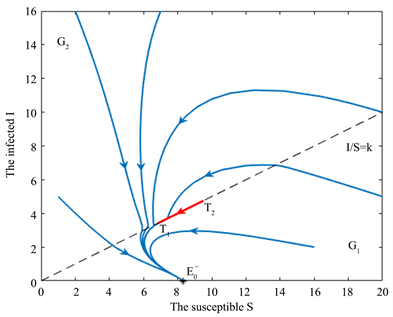
Figure 3. The parameters are selected as follows: $A=5,\beta =0.1,{\eta }_1=0.6,{\eta }_2=0.9,v=0.6,k=0.5$

图3. 参数选取 $A=5,\beta =0.1,{\eta }_1=0.6,{\eta }_2=0.9,v=0.6,k=0.5$

情形2 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$

定理4.2 当 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ 时，地方病平衡点 $E_1$ 是全局渐近稳定的。

证明 由条件 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 可得 $\frac{I_1}{S_1}=\frac{A\beta -{\eta }_1{\eta }_2}{{\eta }_2^2}<k$ ，此时 $E_1$ 为实平衡点。由条件 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ 可得 $\frac{I_2}{S_2}=\frac{A\beta -{\eta }_1\left({\eta }_2+v\right)}{\beta \left({\eta }_2+v\right)}<k$ ，此时 $E_2$ 为虚平衡点。

因为 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2<0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ ，由引理3.1可得， $S_p<S_T^1<S_T^2$ 此时滑模域上没有伪平衡点。由 $f\left(S\right)$ 的性质知，当 $S\in \left(S_T^1,S_T^2\right)$ 时，有 $f\left(S\right)<0$ ，即滑模域上的解轨线沿着滑模向下滑动。

由于系统(1.1)不存在滑模极限环以及穿越极限环，所以 $E_1$ 是全局渐近稳定的，如图4所示。

Figure 4. The parameters are selected as follows: $A=8,\beta =0.04,{\eta }_1=0.3,{\eta }_2=0.8,v=0.5,k=0.5$

图4. 参数选取 $A=8,\beta =0.04,{\eta }_1=0.3,{\eta }_2=0.8,v=0.5,k=0.5$

情形3 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 。

定理4.3 当 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ 时，伪平衡点 $E_p$ 是全局渐近稳定的。

证明由条件 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 可得

$\frac{I_1}{S_1}=\frac{A\beta -{\eta }_1{\eta }_2}{{\eta }_2^2}>k,$

此时 $E_1$ 为虚平衡点，类似可得， $E_2$ 为虚平衡点。

因为 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k<0$ ，由引理3.1可得， $S_T^1<S_p<S_T^2$ ，此时滑模域 ${\Sigma }_1$ 存在伪平衡点 $E_p$ 。由 $f\left(S\right)$ 的定义可知 $f^{\prime }\left(S_p\right)<0$ ，即伪平衡点是稳定的。当 $S\in \left(S_T^1,S_p\right)$ 时，有 $f\left(S\right)>0$ ，当 $S\in \left(S_p,S_T^2\right)$ 时，有 $f\left(S\right)<0$ ，说明滑模域 ${\Sigma }_1$ 上的解轨线将收敛到 $E_p$ 。

由于系统(1.1)不存在滑模极限环以及穿越极限环，所以 $E_1$ 是全局渐近稳定的，如图5所示。

定理4.4 当 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k>0$ 时，地方病平衡点 $E_2$ 是全局渐近稳定的。

证明由条件 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 可得 $\frac{I_1}{S_1}=\frac{A\beta -{\eta }_1{\eta }_2}{{\eta }_2^2}>k$ ，此时 $E_1$ 为虚平衡点。由条件 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k>0$ 可得 $\frac{I_2}{S_2}=\frac{A\beta -{\eta }_1\left({\eta }_2+v\right)}{\beta \left({\eta }_2+v\right)}>k$ ，此时 $E_2$ 为实平衡点。

Figure 5. The parameters are selected as follows: $A=15,\beta =0.1,{\eta }_1=0.55,{\eta }_2=0.8,v=0.9,k=0.6$

图5. 参数选取 $A=15,\beta =0.1,{\eta }_1=0.55,{\eta }_2=0.8,v=0.9,k=0.6$

因为 $A\beta -k{\eta }_2^2-{\eta }_1{\eta }_2>0$ 且 $A\beta -{\eta }_1\left({\eta }_2+v\right)-{\eta }_2\left({\eta }_2+v\right)k>0$ ，由引理3.1可得， $S_T^1<S_T^2<S_p$ 此时滑模域上没有伪平衡点。由 $f\left(S\right)$ 的性质知，当 $S\in \left(S_T^1,S_T^2\right)$ 时，有 $f\left(S\right)>0$ ，即滑模域上的解轨线沿着滑模向上滑动。

由于系统(1.1)不存在滑模极限环以及穿越极限环，所以 $E_2$ 是全局渐近稳定的，如图6所示。

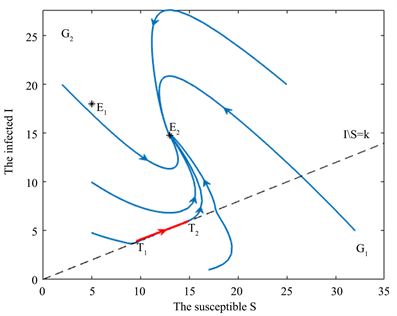
Figure 6. The parameters are selected as follows: $A=10,\beta =0.1,{\eta }_1=0.2,{\eta }_2=0.5,v=0.8,k=0.4$

图6. 参数选取 $A=10,\beta =0.1,{\eta }_1=0.2,{\eta }_2=0.5,v=0.8,k=0.4$

5. 总结

文章研究了一类Lotka-Volterra Filippov型植物传染病模型，根据易感植株的数量和感染植株的数量比例来决定是否采取控制措施，这导致模型的分界线是一条倾斜的斜线，大部分的Lotka-Volterra Filippov型植物传染病模型的分界线是一条水平线 [5] [6] ，这是本文的新颖点。

对于模型的动力学行为分析，首先分析了模型解的有界性和和正解性，保证了模型的生物学意义；其次，分别分析了在不同区域上以及滑模区域上系统的动力学行为，在通过构造合适的Lyapunov函数分析系统在两个子区域上的动力学行为，分别得到地方病平衡点 $E_1$ 、 $E_2$ 是渐近稳定的，通过Filippov理论分析系统在滑模区域上的动力学行为；在分析系统的全局动力学行为时，给出两个引理并给出详细的证明，这两个引理帮助我们排出了系统可能存在的滑模极限环和穿越极限环，再通过构造合适的Lyapunov函数分析系统的解的渐近稳定性，构造合适的Lyapunov函数这是本文的另一新颖点。根据参数的取值分为四种情况，分别分析了这四种情况下系统的全局动力行为，以定理的形式叙述得到的结果。最后通过数值模拟验证结果。

致 谢

感谢国家自然科学基金项目(编号：12201199)；湖南省自然科学基金项目(编号：2020JJ5014、2022JJ40021)；湖南省教育厅项目(编号：21B0722、21C0660、21C0665)资助。

参考文献