1. 引言
丙型病毒性肝炎简称丙型肝炎,是由丙型肝炎病毒(HCV)感染引起的,潜伏期通常在2~26周,平均50天 [1] ,主要传播途径为血液传播、性传播、母婴传播等。丙型肝炎主要的临床表现为急性的、慢性的和肝硬化。在没有任何治疗措施的情况下,约有30%的感染者会在6个月内自行清除病毒,55%~85%的感染者会发展为慢性肝炎,其中15%~30%的慢性患者在未治疗情况下20年内会进一步发展为肝癌 [2] 。由于丙型肝炎特殊的传播途径,导致其在不同人群中的感染概率会有差异。丙型肝炎的高危人群主要包括反复输入血液或血液制品人群、静脉吸毒人群、有家族病史人群和艾滋病人群等 [3] ,普通人群接触丙型肝炎病毒并且患病的几率远低于高危人群,普及丙型肝炎防治知识以及进行早期筛查治疗对疾病的防控尤为重要。
一般传染病模型常常假设人群是均匀混合的,忽略了人群间的异质性,例如年龄、性别等。在现实生活当中,个体间是具有差异性的。在某些特定的情况下,人群的异质性是不能够被忽略的 [4] 。Hu等人 [3] 充分考虑人口统计学、从传染者向易感者转移和个体间接触异质性等的情况,在复杂异质性网络上构建了一类SIRS数学模型,分析得到了两类平衡点的存在性和全局渐近稳定性。并提出随机免疫、目标群体免疫和熟人免疫三种免疫策略对异质性网络模型的影响,结果表明目标群体免疫是控制疾病传播的有效途径,可以降低基本再生数。桑在文献 [5] 中建立了一类具有性别差异和性行为风险的生殖器疱疹异质性模型,按照性别及性行为风险程度将人群分为女性高危人群、女性低危人群和男性三个群体,建立了相应的多群组模型,对模型进行了动力学分析。通过构建Lyapunov函数和依据Lasalle不变集原理证明了平衡点的稳定性,得到疾病的控制效果由基本再生数决定。Lu等人 [6] 建立了一类具有异质混合人群的动态疫苗接种模型,分析了接种疫苗对疫情暴发总体风险的影响。2023年,陈等人在文献 [7] 中构建了一类具有早期筛查的丙型肝炎传染病模型并进行了动力学分析。目前对于丙型肝炎人口异质性研究的相关文献较少,所以本文将依据丙型肝炎的传播机理,深入探讨人口异质性对丙型肝炎传播的影响。
2. 模型建立
我们将总人群N分为高危人群和一般人群,高危人群主要包括输血或血液制品的患者和供血者、艾滋病患者、共用注射器吸毒者和多性伴侣者,其余的为一般人群。基于以往文献的研究成果,建立具有人口异质性和早期筛查的丙型肝炎传染病模型。设
表示易感者仓室,
表示急性感染者仓室,
表示慢性感染者仓室,T表示治疗者仓室,
表示恢复者仓室,传播流程图如下图1:
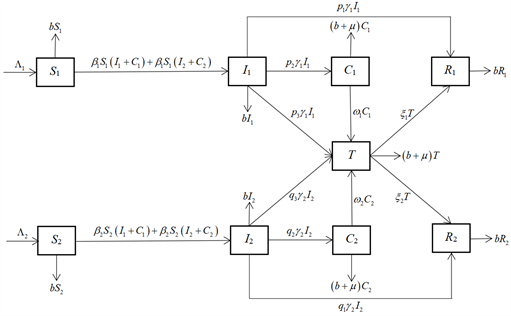
Figure 1. The flow chart of a hepatitis C epidemic model with population heterogeneity
图1. 具有人口异质性的丙型肝炎模型流程图
相应的传染病模型为:
(1)
各参数的生物意义如表1:


Table 1. Biological significance of parameters
表1. 参数生物意义
其中
表示一般人群,
表示高危人群;
,
。
记总人数
,对于任意的
,系统(1)的解
在
是非负有界的。设
是系统(1)的解半流
关于
的
极限集,由系统(1)可得
根据 [8] 中的定理可知系统(1)的可行域为:
(2)
3. 平衡点和控制再生数
再生数 [9] 是传染病研究中一个重要的参量。为阻止传染病的蔓延,人们往往会依据疾病的传播特点采取一些相应的控制措施。控制再生数表示在外界干预措施下,一个感染者在其感染期内平均能传染多少二代确诊病例。当控制再生数小于零时,表示疫情能够得到有效控制并且会逐渐消除;当控制再生数大于零时,传染病会形成地方病。
显然,模型(1)存在一个无病平衡点
,下面利用下一代矩阵的方法 [10] 来
计算模型(1)的控制再生数。可得
因而控制再生数为:
(3)
4. 敏感性分析
敏感性分析 [11] 对于确定影响疾病传播的重要因素至关重要。变量
关于
的敏感性指数定义为:
下面将探讨
对一些参数的敏感性:
由上可知,一般人群中的控制再生数
是传染率系数
和急性感染者转至慢性感染者的比例
的递增函数,并且对
的变化最为敏感;高危人群中的控制再生数
也是传染率系数
和急性感染者转至慢性感染者的比例
的递增函数,并且对
的变化最为敏感。因而可以通过降低感染者与一般人群的接触率来减少传染率系数
,使控制再生数降低;也可以通过提高医疗手段精准检测,早发现并尽早干预和治疗,降低急性感染者向慢性感染者转化的比例,从而控制丙型肝炎的传播。
5. 数值模拟
图2揭示了控制再生数
对两类人群传染率系数
和
的敏感性的变化趋势,可以看出
随着
和
的增加而增加,并且随着
增加的趋势更加明显,因此适当降低高危人群与总人群的接触率,可以有效地降低丙型肝炎的传播。
图3刻画了控制再生数
对两类人群中急性转变至慢性的比例
和
的敏感性变化趋势,可以看出
随着
和
的增加而增加,并且随
增加的趋势更加明显。由于在高危人群中,有
,固定急性自愈的比例
不变,当
增加时,
会随之降低,故
随着
的增加而降低,同理可得在一般人群中
随着
的增加而降低,所以早筛查早治疗可以使模型的控制再生数降低,能有效控制疾病的传播。
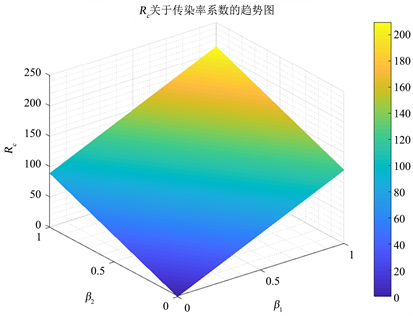
Figure 2. The trend chart of Rc corresponding to the infection rate coefficient
图2. Rc关于传染率系数的趋势图

Figure 3. The trend chart of Rc corresponding to the transmission proportion from the acute to the chronic
图3. Rc关于急性转变至慢性比例的趋势图
6. 结论
本文研究了丙型肝炎在两类人群中的传播情况,考虑了不同人群传染率系数和急性转变至慢性的比率的异质性因素,构建一类丙型肝炎传染病模型。首先计算得到无病平衡点
的存在性,其次利用下一代矩阵方法求出控制再生数
,最后对模型进行了敏感性分析和数值模拟。数值模拟的结果表明控制再生数
随着传染率系数
的增加而增加,并且对
增加的趋势更为明显;
随着急性转变至慢性的比例
的增加而增加,并且随着高危人群的
增加的趋势更为明显。当控制高危人群中
的参数不变,可以得到
随着
的增加而减少,因此增加对高危人群中急性丙型肝炎患者的早期筛查及治疗,可以更有效地减少控制再生数,进而阻止丙型肝炎在人群中的蔓延。
基金项目
北京市教育委员会科研计划项目(SZ202110016008);北京建筑大学研究生教育教学质量提升项目资助(J2023021)和研究生创新项目(PG2023145)。
参考文献
NOTES
*通讯作者。