一类椭变曲线

A Kind of Elliptic Transform Curves

摘要: 对圆按一定方向一定比例做压缩或拉伸变换可以得到椭圆。本文提出一类参数方程，通过绘图实验和分析，发现是一种对椭圆进行压拉变换，可得到卵圆和心形线，并获得了这类曲线的面积、质心坐标、转动惯量、旋转卵形体的体积等重要公式。

Abstract: The ellipse can also be regarded as a figure obtained by compressing or stretching a circle in a cer-tain direction in a certain proportion. In this paper, a kind of parametric equation is presented. Through drawing experiment and analysis, it is a transformation of compression and stretching of ellipse to obtain oval and cardioid. The important formulas of the area, centroid coordinate, mo-ment of inertia and volume of rotating oval ball are calculated.

1. 引言

关于圆 [1] 和椭圆 [2] ，人们对其定义、几何性质、物理意义及其成因已有非常丰富的认识 [3] 。而对卵圆和卵形曲线的认识和研究相对滞后，对卵形线的深入研究很有必要。

对圆按一定方向一定比例作压缩或拉伸变换可以得到椭圆 [4] 。本文对椭圆进行一种纵向上压下拉变换，得到一类由椭圆变换成的曲线，简称为椭变曲线。对椭变曲线进行绘图实验和定形分析，发现它其实是卵圆或心形线，并推导出这类椭变曲线所围图形的面积、所围图形的质心、所围图形转动惯量、所围图形的旋转卵形体的体积等重要公式。

2. 定义

定义1：设

$e>0,c>0,k>0$ (1)

$\{\begin{array}{l}x=c\cos t\\ y=e\left(1-k\sin t\right)\sin t\end{array},t\in \left[-\frac{\pi }{2},\frac{3\pi }{2}\right]$ (2)

则称(2)的图形曲线为椭变曲线，称坐标系原点为的中心，三个参数e，c，k分别称为的轴半径、对称半径、定形系数，当 $0<k\le 0.5$ 时称为椭变卵圆，当 $k>0.5$ 时称为椭变心形线。

3. 椭变曲线的定形分析

通过对(2)中的参数e，c，k的数值有规律的改变，得到其曲线的不同图形。通过绘图实验，得到曲线不同参数下的形状和变化趋势，分析总结曲线的形状及其性质。

先限定轴半径e和对称半径c，而定形系数k则从0不断增大，来观察(2)曲线的图形变化。

现取 $e=4$ ， $c=3$ ，而k分别取三组数值进行绘图实验：

① $k=0.1,k=0.2,k=0.3,k=0.5$ ，曲线形状变化情况如图1所示；

② $k=0.6,k=0.7,k=0.8,k=0.9$ ，曲线形状变化情况如图2所示；

③ $k=1,k=1.3,k=1.7,k=2$ ，曲线形状变化情况如图3所示。

当 $k=0$ 时，则(2)变成

$\{\begin{array}{l}x=c\cos t\\ y=e\sin t\end{array},t\in \left[-\frac{\pi }{2},\frac{3\pi }{2}\right]$ (3)

显然(3)为长半轴为e，短半轴为c的椭圆方程。

由图1可以发现，随着k值的增大，曲线图形整体逐渐下移，曲线顶端上凸曲率逐渐变小，曲线形状呈卵圆形，当 $k=0.5$ 时，曲线顶端局部呈直线状。

由图2可以发现， $k>0.5$ 后，曲线图形继续整体下移，曲线顶端形状发生凹陷，随着k值的增大，曲线顶端凹陷越来越明显，曲线形状呈心形状。

由图3可以发现，当 $k>1$ 后，曲线形状还是呈心形状，曲线顶端凹陷的谷底越过x轴，随着k值的增大，曲线整体被向下拉长。

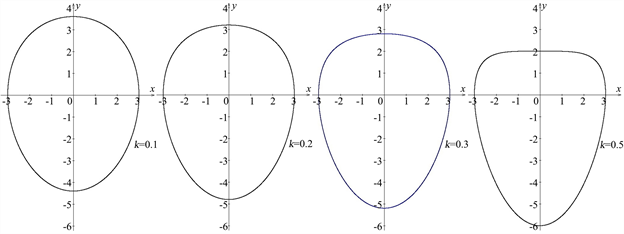
Figure 1. Limited axis radius e = 4, symmetric radius c = 3, shaping coefficient k = 0.1, 0.2, 0.3, 0.5, curve shape change

图1. 限定轴半径e = 4，对称半径c = 3，定形系数k = 0.1，0.2，0.3，0.5，曲线形状变化情况

Figure 2. Limited axis radius e = 4, symmetric radius c = 3, shaping coefficient k = 0.6, 0.7, 0.8, 0.9, curve shape change

图2. 限定轴半径e = 4，对称半径c = 3，定形系数k = 0.6，0.7，0.8，0.9，曲线形状变化情况

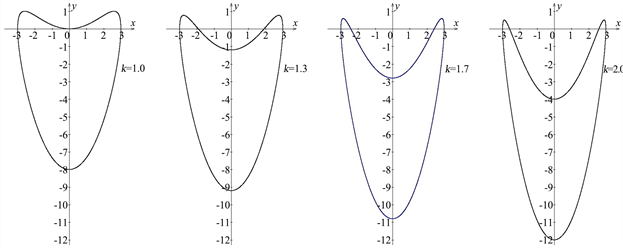
Figure 3. Limited axis radius e = 4, symmetric radius c = 3, shaping coefficient k = 1.0, 1.3, 1.7, 2.0, curve shape change

图3. 限定轴半径e = 4，对称半径c = 3，定形系数k = 1.0，1.3，1.7，2.0，曲线形状变化情况

通过绘图实验可以总结出，椭变曲线(2)可通过对椭圆(3)按定形系数k的纵向上压下拉法的变换(简称为H变换)而得到，且y轴是椭变曲线(2)的对称轴，变化过程中，曲线在x轴上的端点保持不动。可以得出当 $0<k\le 0.5$ 时，H变换把椭圆(3)变换成卵圆；当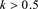时，H变换把椭圆(3)变换成心形线。

取 $e=4,c=3$ ，当 $k=0,0.5,0.8,1,1.3$ 时的曲线整体形状随k值的变化规律如图4所示。

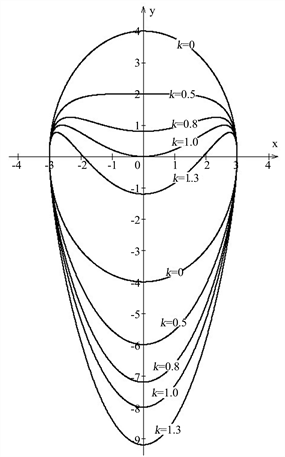
Figure 4. Curve shape changes with the change of k value

图4. 随k值改变，曲线形状整体变化情况

从图4看出，对椭圆(3)实施H变换的实质，是使椭圆(3)在y轴上的上、下两个端点位置同时向下移动ke单位，但椭变曲线的长轴长度2e保持不变，在x轴上的短轴及端点位置保持不变，椭圆图形被上压下拉。随k值的增大，在变形过程中形成卵圆和心形线。而椭圆则是卵圆的特殊形式 [5] 。

4. 椭变曲线的面积

定理1：设椭变曲线(2)的轴半径为e，对称半径为c，所围图形面积为S，则

$S=\frac{\pi }{2}ec$ (4)

证明：由文献( [6] , p. 204)，知

$S=\frac{1}{2}{\displaystyle {\int }_0^{2\pi }\left(x{y}^{\prime }-y{x}^{\prime }\right)\text{d}t}$ (5)

将(2)及其导数代入(5)并化简，得

$\begin{array}{l}S=\frac{1}{2}{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}\left[c\cos t\left(e\cos t-ke\sin 2t\right)+e\left(1-k\sin t\right)\sin t\cdot c\sin t\right]\text{d}t}\\ =\frac{ec}{2}[{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}\left({\sin }^{2}t+{\cos }^{2}t\right)\text{d}t}-{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}k\sin 2t\cos t}\text{d}t-{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}k{\sin }^{3}t}\text{d}t]\end{array}$

而

${\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}\left({\sin }^{2}t+{\cos }^{2}t\right)\text{d}t}={\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}\text{d}t}=2\pi$

${\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}k\sin 2t\cos t}\text{d}t=-{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}2k{\cos }^{2}t\text{d}\cos t}=-2k{\displaystyle {\int }_0^0{u}^2\text{d}u}=0$

$\frac{c}{4}{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}k{\sin }^{3}t\text{d}t}=-k{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{3\pi }{2}}\left(1-{\cos }^{2}t\right)\text{d}\cos t}=-k{\displaystyle {\int }_0^0\left(1-u^2\right)\text{d}u}=0$

故 $S=\frac{ec}{2}2\pi =\pi ec$ ，即(4)成立。

注1：以e，c为长、短半轴的椭圆面积为 $\pi ec$ ，而对椭圆(3)实施H变换后得到椭变曲线(2)，但其面积仍为 $\pi ec$ ，与k无关，故H变换为“等积变换”。

5. 椭变曲线所围图形的质心

定理2：设椭变曲线(2)的轴半径为e，对称半径为c，定形系数为k，曲线所围图形的质心为 $\left(\bar{x},\bar{y}\right)$ ，则

$\{\begin{array}{l}\bar{x}=0\\ \bar{y}=-\frac{3}{4}ke\end{array}$ (6)

证明：由对称性显然有 $\bar{x}=0$ 。

设椭变曲线(2)的上半部为 $y_2\left(x\right)$ ，下半部为 $y_1\left(x\right)$ ，则由(2)可得

$y_2\left(x\right)=\frac{e}{c^2}\left[c\sqrt{c^2-x^2}-k\left(c^2-x^2\right)\right]$ (7)

$y_1\left(x\right)=-\frac{e}{c^2}\left[c\sqrt{c^2-x^2}+k\left(c^2-x^2\right)\right]$ (8)

又设卵形曲线(2)所围图形对x轴的静力矩为 $M_x$ ，则由文献( [7] , p. 229)知

$M_x=\frac{1}{2}{\displaystyle {\int }_{-c}^c\left(y_2^2-y_1^2\right)\text{d}x}$ (9)

将(7)和(8)代入(9)并化简，得

$M_x=-\frac{2k{e}^2}{2}{\displaystyle {\int }_{-c}^c\left(c^2-x^2\right)\sqrt{c^2-x^2}}\text{d}x$

上式中令 $x=c\sin t$ ，换元积分之，得

$M_x=-\frac{2k{e}^2}{c^3}{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{c}^4{\cos }^{4}t}dt=-2k{e}^{2}c{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{1}{8}\left(3+4\cos 2t+\cos 4t\right)\text{d}t}=-\frac{kc{e}^{2}c}{4}{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}3\text{d}t}=-\frac{3\pi }{4}k{e}^{2}c$ (10)

又

$\bar{y}=\frac{M_x}{S}$ (11)

将(4)和(10)代入(11)得 $\bar{y}=-\frac{3}{4}ke$ ，故(6)成立。

6. 椭变曲线所围图形的转动惯量

定理3：设椭变曲线(2)的轴半径为e，对称半径为c，定形系数为k，曲线所围图形绕y轴的转动惯量为 $I_y$ ，则

$I_y=\frac{1}{4}M{c}^2$ (12)

其中

$M=\pi ec\rho$ (13)

是面密度为常数 $\rho$ 的卵形曲线薄片的质量。

证明：由文献( [7] , p. 239)知

$I_y={\displaystyle {\int }_{-c}^c\rho x^2\left(y_2-y_1\right)\text{d}x}$ (14)

将(7)和(8)代入(14)并化简，得

$\begin{array}{l}{I}_y=\frac{2e\rho }{c}{\displaystyle {\int }_{-c}^c{x}^2\sqrt{c^2-x^2}}\text{d}x=\frac{4e\rho }{c}{\displaystyle {\int }_0^c{x}^2\sqrt{c^2-x^2}}\text{d}x=\frac{4e\rho }{c}{\displaystyle {\int }_0^{\frac{\pi }{2}}{c}^3{\sin }^{2}t\cdot \cos t\text{d}\sin t}\\ =4e{c}^3\rho {\displaystyle {\int }_0^{\frac{\pi }{2}}{\left(\sin t\cos t\right)}^2}\text{d}t=e{c}^3\rho {\displaystyle {\int }_0^{\frac{\pi }{2}}{\left(\sin 2t\right)}^2}\text{d}t=e{c}^3\rho {\displaystyle {\int }_0^{\frac{\pi }{2}}\frac{1-\cos 4t}{2}\text{d}t}\\ =\frac{e{c}^3\rho }{2}{\left[t-\frac{1}{4}\sin 4t\right]}_0^{\frac{\pi }{2}}=\frac{\pi }{8}e{c}^3\rho =\frac{1}{4}M{c}^2\end{array}$

其中 $M=\pi ec\rho$ 。

7. 椭变曲线旋转卵形体的体积

定理4：设椭变曲线(2)的轴半径为e，对称半径为c，定形系数为k，曲线所围图形绕y轴旋转而成的旋转卵形体的体积为V，则

$V=\frac{4}{3}\pi e{c}^2$ (15)

证明：由文献( [8] , p. 278)及(2)知，旋转卵形体的体积

$\begin{array}{l}V=\pi {\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{x}^2\left(t\right)y^{\prime }\left(t\right)\text{d}t}=\pi {\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{c}^2{\cos }^{2}t\cdot \left[e\cos t-ke\cos t\sin t\right]\text{d}t}\\ =\pi e{c}^2{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\cos }^{3}t\text{d}t}-\pi e{c}^{2}k{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\cos }^{3}t\sin t\text{d}t}\\ =\pi e{c}^2{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\frac{3\cos t+\cos 3t}{4}\text{d}t}+\pi e{c}^{2}k{\displaystyle {\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\cos }^{3}t\text{d}\cos t}\\ =\pi e{c}^2{\left[\frac{3}{4}\sin t+\frac{1}{12}\sin 3t\right]}_{-\frac{\pi }{2}}^{\frac{\pi }{2}}+\pi e{c}^{2}k{\displaystyle {\int }_0^0{u}^3}\text{d}u\\ =\pi e{c}^2\cdot \frac{4}{3}+0=\frac{4}{3}\pi e{c}^2\end{array}$

故(15)成立。

注2：由(15)知，其体积与定形系数k无关，即与椭圆(3)绕y轴旋转而成的椭球的体积是相同的，这又一次佐证了H变换是“等积变换”。

8. 椭变曲线的周长

定理8：设椭变曲线(2)的轴半径为e，对称半径为c，定形系数为k，椭变曲线的周长为l，则

$l={\displaystyle {\int }_0^{2\pi }\sqrt{{\text{c}}^2{\sin }^{2}t+e^2\left(1-2k\sin t\right){\cos }^{2}t}\text{d}t}$ (16)

证明：由文献( [7] , p. 166)的弧长公式

$l={\displaystyle {\int }_0^{2\pi }\sqrt{{x^{\prime }}^2\left(x\right)+{y^{\prime }}^2\left(x\right)}}\text{d}t$ (17)

将(2)的导数代入(17)并化简即得(16)。

注3：当 $k=0$ 时，(16)变成

$l={\displaystyle {\int }_0^{2\pi }\sqrt{{\text{c}}^2{\sin }^{2}t+e^2{\cos }^{2}t}\text{d}t}$ (18)

(18)正是长半轴为e，短半轴为c的椭圆的周长公式，这也佐证了公式(16)的正确性。

9. 结语

众所周知，圆、椭圆、双曲线、抛物线等二次曲线已被研究得十分完善，相对来说，人们对卵圆的研究进展较为缓慢。时至今日，对卵圆还没有公认的明确的统一定义。对圆按一定方向一定比例做压缩或拉伸变换可以得到椭圆，椭圆是圆的一个扩展，根据这一思路，本文对椭圆再进行单向压反向拉的H变换，提出一类参数方程，通过绘图实验和分析，得到了面积不变的卵圆或心形线，并获得了这类曲线的面积、周长、质心坐标、转动惯量、旋转卵形体的体积等重要公式，给卵圆和心形线的研究提出一种新思路、新方法。

参考文献

NOTES

^*通讯作者。