一种充分光滑分数阶投影算子的构造方法

A Construction Method of Sufficiently Smooth Fractional-Order Projection Operator

摘要: 本文首先介绍了Caputo型分数阶导数的定义及其满足的相关引理。其次为了构造自适应律，提出了一种充分光滑的分数阶参数投影算子构造方法。最后给出了所提投影算子满足的一些性质，并提供了严密的证明。

Abstract: This paper first introduces the definition of Caputo type fractional-order derivative and the correla-tion lemma about it. Secondly, a construction method of sufficiently smooth fractional-order projec-tion operator is proposed for adaptive laws. Finally, some properties satisfied by the proposed pro-jection operator are given, and a strict proof is provided.

1. 引言

投影算子是一种常用的自适应控制算法，它的主要作用是将参数投影到一个预定义的空间或集合中，从而限制参数的范围，以满足特定的约束条件。一般来说，基于投影的参数自适应律是不连续的，这违反了微分方程经典解存在的Lipschitz条件。因此，从现实的角度来看，这种不连续性是不可取的。为了消除这个限制，Pomet等人在 [1] 中通过在凸集周围引入边界层，从而得到Lipschitz连续投影算子。在此基础上，Cai等人在 [2] 中利用更强的任意多次连续可微性取代了Lipschitz连续性，同时对其他投影性质进行了微调。进而上述投影算子的结论在理论研究和实际工程领域中也得到越来越广泛的应用 [3] [4] [5] 。然而，上述投影算子只适用于整数阶系统的参数自适应控制中，分数阶系统是对传统控制理论中的整数阶系统的扩展，可以更准确地描述具有非刚性的动态系统，如热力学系统、柔性系统等。进而在车辆悬架系统、分形与混沌、电池管理系统、机器人等领域都有广泛的应用 [6] [7] [8] 。因此，分数阶系统控制设计问题目前已经成为学者们研究的热点问题。但目前还没有分数阶投影算子用于抑制参数的范围，因此本文基于分数阶相关定义和引理，给出了一种充分光滑的分数阶参数投影算子构造方法。总结了所提投影算子满足的四条性质，并予以证明。

2. Caputo型分数阶导数定义及相关引理

定义1 [6] ：假设 $P:\left[t_0,+\infty \right)\to R$ 是连续可微函数，它的 $\alpha$ 阶Caputo型分数阶导数可定义：

${}_0{}^{C}D{}_t^{\alpha }P\left(t\right)=\frac{1}{\Gamma \left(\omega -\alpha \right)}{\displaystyle {\int }_0^t\frac{P^{\left(\omega \right)}\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha +1-\omega }}\text{d}\tau }$ (1)

其中 $\omega -1\le \alpha \le \omega$ ， $\omega$ 为正整数。 $\Gamma (\cdot )={\displaystyle {\int }_0^{+\infty }{\tau }^{\cdot -1}{\text{e}}^{-\tau }}\text{d}\tau$ Gamma 函数，且满足 $\Gamma \left(1\right)=1$ 。

引理1 [9] ：若 $\hslash \left(t\right)$ 是一个光滑函数，则下面不等式成立

$\frac{1}{2}{}_0{}^{C}D{}_t^{\alpha }\left({\hslash }^{\text{T}}\left(t\right)\hslash \left(t\right)\right)\le {\hslash }^{\text{T}}\left(t\right){}_0{}^{C}D{}_t^{\alpha }\hslash \left(t\right)$ (2)

引理2 [10] ：假设 $V=\frac{1}{2}{z}^2$ ，若 $z{}_0{}^{C}D{}_t^{\alpha }z<0$ ，则有。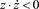

3. 分数阶投影算子

若 $\stackrel{⌣}{\theta }\in \Omega :\left\{\stackrel{⌣}{\theta }|\Vert \stackrel{⌣}{\theta }\Vert \le {\stackrel{⌣}{\theta }}_0\right\}$ 是一个未知的常参数，其中 ${\stackrel{⌣}{\theta }}_0>0$ 。令 $\widetilde{\stackrel{⌣}{\theta }}=\stackrel{⌣}{\theta }-\widehat{\stackrel{⌣}{\theta }}$ 为参数估计误差，我们给出一

种充分光滑的分数阶投影算子构造方法，具体表示如下：

${}_0{}^{C}D{}_t^{\alpha }\widehat{\stackrel{⌣}{\theta }}=\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)=\stackrel{⌣}{\mu }-\frac{{\stackrel{⌣}{\eta }}_1{\stackrel{⌣}{\eta }}_2}{2{\left({\stackrel{⌣}{\epsilon }}^2+2\epsilon {\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}\nabla p\left(\widehat{\stackrel{⌣}{\theta }}\right)$ (3)

其中

$p\left(\widehat{\stackrel{⌣}{\theta }}\right)={\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2$ (4)

${\stackrel{⌣}{\eta }}_1=\{\begin{array}{l}{p}^{n+1}\left(\widehat{\stackrel{⌣}{\theta }}\right),\text{if}p\left(\widehat{\stackrel{⌣}{\theta }}\right)>0\\ 0,\text{else}\end{array}$ , ${\stackrel{⌣}{\eta }}_2=\frac{1}{2}\nabla p{\left(\widehat{\stackrel{⌣}{\theta }}\right)}^{\text{T}}\stackrel{⌣}{\mu }+\sqrt{{\left(\frac{1}{2}\nabla p{\left(\widehat{\stackrel{⌣}{\theta }}\right)}^{\text{T}}\stackrel{⌣}{\mu }\right)}^2+{\stackrel{⌣}{\delta }}^2}$ (5)

其中 $\stackrel{⌣}{\epsilon }>0$ ， $\stackrel{⌣}{\delta }>0$ ，符号表示梯度。

定理1：若 $\widehat{\stackrel{⌣}{\theta }}\left(0\right)\in \Omega$ ，所提分数阶投影算子(3)~(5)满足如下性质：

1. $\Vert \widehat{\stackrel{⌣}{\theta }}\left(t\right)\Vert \le {\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }$ , $\forall t\ge 0$ .

2. $\widetilde{\stackrel{⌣}{\theta }}\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\ge {\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }$ .

3. $\Vert \text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\Vert \le \Vert \stackrel{⌣}{\mu }\Vert \left(1+{\left(\frac{{\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }}{{\stackrel{⌣}{\theta }}_0}\right)}^2\right)+\frac{{\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }}{{\stackrel{⌣}{\theta }}_0^2}\stackrel{⌣}{\delta }$ .

4. $\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)$ is $C^n$ .

证明：1. 当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)\le 0$ ，由(4)可得 $\Vert \widehat{\stackrel{⌣}{\theta }}\Vert \le {\stackrel{⌣}{\theta }}_0<{\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }$ 。取 $V_{\widehat{\stackrel{⌣}{\theta }}}=\frac{1}{2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}$ ，根据引理1，可得

${}_0{}^{C}D{}_t^{\alpha }{V}_{\widehat{\stackrel{⌣}{\theta }}}\le {\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}{}_0{}^{C}D{}_t^{\alpha }\widehat{\stackrel{⌣}{\theta }}={\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }-\frac{{\stackrel{⌣}{\eta }}_1{\stackrel{⌣}{\eta }}_2}{2{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}$ (6)

当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)>0$ 且 $\nabla p{\left(\widehat{\stackrel{⌣}{\theta }}\right)}^{\text{T}}\stackrel{⌣}{\mu }=2{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }\le 0$ 时，可得下面不等式

${}_0{}^{C}D{}_t^{\alpha }{V}_{\widehat{\stackrel{⌣}{\theta }}}\le -\frac{{\stackrel{⌣}{\eta }}_1{\stackrel{⌣}{\eta }}_2}{2{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}<0$ (7)

由于 ${\stackrel{⌣}{\eta }}_1,{\stackrel{⌣}{\eta }}_2>0$ ， $\Vert \widehat{\stackrel{⌣}{\theta }}\Vert$ 收敛到了 $\Omega$ 中，且 $\widehat{\stackrel{⌣}{\theta }}\left(0\right)\in \Omega$ 。当 $\nabla p{\left(\widehat{\stackrel{⌣}{\theta }}\right)}^{\text{T}}\stackrel{⌣}{\mu }=2{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }>0$ ，可推导出

$\begin{array}{c}{}_0{}^{C}D{}_t^{\alpha }{V}_{\widehat{\stackrel{⌣}{\theta }}}\le {\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }-\left[\frac{{\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2\right)}^{n+1}}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\right]{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }-\frac{{\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2\right)}^{n+1}}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\sqrt{{\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }\right)}^2+{\stackrel{⌣}{\delta }}^2}\\ \le \left[1-\frac{{\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2\right)}^{n+1}}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\right]{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }\end{array}$

其中 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)={\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2>0$ 或 ${\Vert \widehat{\stackrel{⌣}{\theta }}\Vert }^2>{\stackrel{⌣}{\theta }}_0^2$ 。假设 ${\Vert \widehat{\stackrel{⌣}{\theta }}\Vert }^2={\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }$ ，其中 $\stackrel{⌣}{\epsilon }$ 为一任意正常数，则有

${}_0{}^{C}D{}_t^{\alpha }{V}_{\widehat{\stackrel{⌣}{\theta }}}\le \left[1-\frac{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\hat{\theta }\right]{\hat{\theta }}^{\text{T}}\stackrel{⌣}{\mu }=\left(1-\frac{{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}}{{\stackrel{⌣}{\theta }}_0^2}\right){\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }$ (8)

其中 ${\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }>0$ 且 ${\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}>{\stackrel{⌣}{\theta }}_0^2$ 。因此 ${}_0{}^{C}D{}_t^{\alpha }{V}_{\widehat{\stackrel{⌣}{\theta }}}<0$ ， $\Vert \widehat{\stackrel{⌣}{\theta }}\Vert$ 被吸引到 $\Omega$ 中。

2. 当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)\le 0$ ，可得 ${\stackrel{⌣}{\eta }}_1=0$ ，则有 ${\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)={\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }$ 。当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)>0$ ，有

${\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\ge {\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }\iff {\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\left(\text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)-\stackrel{⌣}{\mu }\right)\iff {\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\left[\frac{{\stackrel{⌣}{\eta }}_1{\stackrel{⌣}{\eta }}_2}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}\right]\le 0$ (9)

因为 $\frac{{\stackrel{⌣}{\eta }}_1{\stackrel{⌣}{\eta }}_2}{{\left({\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0\right)}^{n+1}{\stackrel{⌣}{\theta }}_0^2}>0$ ，则要求 ${\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\le 0$ 。显然，下面的不等式是成立的。

$\begin{array}{c}{\widetilde{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}={\left(\stackrel{⌣}{\theta }-\widehat{\stackrel{⌣}{\theta }}\right)}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\\ =-\frac{1}{2}\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}^{\text{T}}\stackrel{⌣}{\theta }\right)-\frac{1}{2}{\left(\widehat{\stackrel{⌣}{\theta }}-\stackrel{⌣}{\theta }\right)}^{\text{T}}\left(\widehat{\stackrel{⌣}{\theta }}-\stackrel{⌣}{\theta }\right)\\ \le -\frac{1}{2}\left({\Vert \widehat{\stackrel{⌣}{\theta }}\Vert }^2-{\Vert \stackrel{⌣}{\theta }\Vert }^2\right)<0\end{array}$ (10)

3. 当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)\le 0$ ， $\Vert \text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\Vert =\Vert \stackrel{⌣}{\mu }\Vert$ 。当 $p\left(\widehat{\stackrel{⌣}{\theta }}\right)>0$ ， ${\stackrel{⌣}{\theta }}_0^2<{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}\le {\left({\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }\right)}^2$ ，根据性质1，可得

$\frac{{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2}{{\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }{\stackrel{⌣}{\theta }}_0}\le 1$ (11)

计算 $\Vert \text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\Vert$ 得到

$\Vert \text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\Vert \le \Vert \stackrel{⌣}{\mu }\Vert +\Vert {\left(\frac{{\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\widehat{\stackrel{⌣}{\theta }}-{\stackrel{⌣}{\theta }}_0^2}{{\stackrel{⌣}{\epsilon }}^2+2\stackrel{⌣}{\epsilon }+{\stackrel{⌣}{\theta }}_0}\right)}^{n+1}\frac{{\stackrel{⌣}{\eta }}_2\widehat{\stackrel{⌣}{\theta }}}{{\stackrel{⌣}{\theta }}_0^2}\Vert \le \Vert \stackrel{⌣}{\mu }\Vert +\Vert \frac{{\stackrel{⌣}{\eta }}_2\widehat{\stackrel{⌣}{\theta }}}{{\stackrel{⌣}{\theta }}_0^2}\Vert$ (12)

因为 ${\stackrel{⌣}{\eta }}_2={\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }+\sqrt{{\left({\widehat{\stackrel{⌣}{\theta }}}^{\text{T}}\stackrel{⌣}{\mu }\right)}^2+{\stackrel{⌣}{\delta }}^2}$ ，(12) 满足

$\Vert \text{Proj}\left(\stackrel{⌣}{\mu },\widehat{\stackrel{⌣}{\theta }}\right)\Vert \le \Vert \stackrel{⌣}{\mu }\Vert +\frac{{\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }}{{\theta }_0^2}\cdot \left(2\Vert \widehat{\stackrel{⌣}{\theta }}\Vert \cdot \Vert \stackrel{⌣}{\mu }\Vert +\stackrel{⌣}{\delta }\right)\le \Vert \stackrel{⌣}{\mu }\Vert \left(1+\frac{2{\left({\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }\right)}^2}{{\stackrel{⌣}{\theta }}_0^2}\right)+\frac{{\stackrel{⌣}{\theta }}_0+\stackrel{⌣}{\epsilon }}{{\stackrel{⌣}{\theta }}_0^2}\stackrel{⌣}{\delta }$ (13)

4. 由于 $C^n$ 函数的乘积依然是 $C^n$ ，假设投影算子(3)中的函数是 $C^n$ ，显然 $\nabla p\left(\widehat{\stackrel{⌣}{\theta }}\right)$ 和 ${\stackrel{⌣}{\eta }}_2\left(\widehat{\stackrel{⌣}{\theta }},\stackrel{⌣}{\mu }\right)$ 是 $C^n$ 。.对于函数 $f\left(\stackrel{⌣}{x}\right)=\{\begin{array}{l}{\stackrel{⌣}{x}}^{n+1},\text{if}\stackrel{⌣}{x}>0\\ 0,\text{else}\end{array}$ ，有

$f^{\left(i\right)}\left(\stackrel{⌣}{x}\right)=\{\begin{array}{l}\frac{\left(n+1\right)!}{\left(n+1-i\right)!}{\stackrel{⌣}{x}}^{n+1-i},\text{if}\stackrel{⌣}{x}>0\\ 0,\text{else}\end{array}$ (14)

因为

$\underset{\stackrel{⌣}{x}\to 0^{+}}{\lim }\frac{f^{\left(i-1\right)}\left(\stackrel{⌣}{x}\right)-f^{\left(i-1\right)}\left(0\right)}{\stackrel{⌣}{x}-0}=\underset{\stackrel{⌣}{x}\to 0^{+}}{\lim }\frac{\frac{\left(n+1\right)!}{\left(n+2-i\right)!}{\stackrel{⌣}{x}}^{n+2-i}}{\stackrel{⌣}{x}}=0$

$\underset{\stackrel{⌣}{x}\to 0^{-}}{\lim }\frac{f^{\left(i-1\right)}\left(\stackrel{⌣}{x}\right)-f^{\left(i-1\right)}\left(0\right)}{\stackrel{⌣}{x}-0}=\underset{\stackrel{⌣}{x}\to 0^{-}}{\lim }\frac{0-0}{\stackrel{⌣}{x}}=0$

则一定可得 ${\stackrel{⌣}{\eta }}_1\left(\widehat{\stackrel{⌣}{\theta }}\right)$ 是 $C^n$ 。至此，定理1证毕。

4. 结论

本文基于Caputo型分数阶导数相关定义和引理，提出了一种充分光滑的分数阶参数投影算子构造方法。进而总结出了所提投影算子满足的四条性质，并给出了详细的证明过程。所提分数阶投影算子一方面可用于分数阶系统中对于参数的抑制问题，还由于其充分光滑的特性适用于对参数反复求导的情况，更利于实际应用。本文的不足之处在于只是给出了数学推导，缺少实际仿真算例的验证。在未来的工作中，我们会对所提投影算子进行实际仿真验证，并推广到高阶参数系统的控制设计中。

基金项目

辽宁工业大学博士科研启动基金(XB2021015)。

参考文献

NOTES

^*通讯作者。