1. 引言
现有解决模型不确定性的方法主要是变量选择和模型平均。在过去的数十年间,相关研究者对变量选择的研究已经十分深入,提出了许多有代表性的方法,如文献 [1] 提出AIC准则和文献 [2] 提出的BIC准则。在某种层面上而言,模型平均是变量选择的一种替代方法。但不像是变量选择只是选择单一的候选模型,模型平均主要是通过对不同的候选模型分配相应权重来进行组合平均,即模型平均的关键问题就是如何选取合适的权重。模型平均相较于变量选择的主要优点是:首先,模型平均可以避免选择到一个单一的效果极为不好的候选模型;其次,模型平均的估计量具有更小的方差;最后,模型平均的预测效果要比单一的候选模型的预测效果要更好。在过去的数十年间,研究者对模型平均的研究取得了一定成果,例如文献 [3] 和文献 [4] 就通过AIC准则和BIC准则来为模型平均选择权重;文献 [5] [6] 首次提出利用候选模型的最小二乘估计量来选择权重,这在模型平均的研究上是一个重大进步,但是该文献中的方法局限是,候选模型的选取是严格嵌套的以及权重被严格的限制在了一个离散的集合上面,且在随机误差项是条件异方差的情形下并不适用;文献 [7] 将文献 [5] [6] 提出的方法进行了改良,即对候选模型的选取可以是非嵌套的以及候选模型的权重可以落在一个连续的集合上面;文献 [8] 提出了新的方法,即利用Jackknife准则来选择候选模型的权重,此方法在随机误差项是条件异方差的情形下也适用且候选模型的权重可以落在一个连续的集合上面。
在许多实际情形,尤其是在经济,社会学等领域中,分位数回归不仅能够比均值回归提供更多的信息而且也更稳健。因此越来越多的研究者将目光放在了分位数回归模型平均上,如文献 [9] 和文献 [10] 首次将模型平均拓展到对分位数模型平均的研究上面;近年来,文献 [11] 提出通过最小化Jackknife准则来选取分位数回归模型平均的最优权重。
值得注意的是,上述文献所用方法选取的权重都是静态的,文献 [12] 首次提出了选取时变权重的模型平均方法,即利用最小化局部Jackknife准则选取时变权重。其通过数值模拟和实证研究说明了,当数据结构发生变化时,时变权重比常值权重有着更小的预测误差。鉴于文献 [12] 中的权重是随着时间的变化而发生变化且是针对均值回归,本文将其拓展到分位数回归模型平均上,且权重变化也不只依赖于时间,而是随着协变量U的变化而变化(U也可以取时间),丰富了权重的变化形式。
本文剩余部分的结构安排如下:第二节主要阐述了变系数分位数回归模型平均估计量和可变权重的选取标准;第三节主要是通过数值模拟展示本文所提方法的表现效果;第四节主要是进行实证分析,第五节为总结。
2. 模型及估计
2.1. 变系数分位数回归模型平均
令
为简单随机样本,满足如下变系数分位数回归模型
, (1)
其中
为被解释变量,
为解释变量,其含有的指标可能是无限维的。
为一维协变量,解释变量X对响应变量Y的影响会随着协变量U的变化而变化。
为误差项,满足
,
为
的条件
分位数。
模型平均方法,又叫组合预测方法,其原理是首先通过一系列候选模型来获得近似的预测,然后通过各种方法或准则计算所有候选模型的权重,最后将利用候选模型计算的近似预测值进行加权求和得到全新的组合预测模型。考虑如下一系列候选模型
,其中第m个模型选取的是
中的某
个元素,
,候选模型数会随着样本数的增大而增多。则第m个近似模型表示为
, (2)
其中
,
,
为第m个模型的渐近误差。对于第m个候选模型(2),
的估计
(3)
其中变系数回归函数的估计
由下式给出
(4)
其中
,其中
为指示函数。
,
,
是核函数,h为窗宽。在后文实验过程中取
,窗宽h取值为
。
令
为权重向量,满足
。当权重
给定的时候,对任意一个样本t,模型(1)中
的模型平均估计量为
. (5)
2.2. Jackknife权重
合理设定所有候选模型的权重向量是模型平均方法的关键,本文利用文献 [8] 提出的Jackknife方法来对权重进行相应估计。
对于第m,
个候选模型来说,条件分位数的Jackknife估计量
,其中
是由在计算
的过程中移除掉第t个观测值后得到的。即
(6)
其中
由下式给出
(7)
当权重向量
给定的时候,
的Jackknife估计量
,则定义
(8)
则权重向量的估计值
. (9)
因此,对任意一个样本t,模型(1)中
最终的模型平均估计量为
.(10)
值得注意的是,与文献 [11] 相比,在本文中候选模型的权重向量
可以随着协变量
的变化而变化,是可变权重的模型平均方法。文献 [12] 首次提出时变的模型平均方法,权重向量随着观测时刻变化而变化,但该文献是基于均值回归模型,本文将该方法应用到变系数的分位数回归模型中,同时本文所提出的权重向量随着协变量
(协变量
也可以取时间)的变化而变化,权重变化形式更加丰富。
2.3. 参数估计步骤
下面将给出本文提出的可变权重的分位数Jackknife模型平均方法(简记为CVQJMA)的参数估计步骤:
步骤1运用式(4)计算出变系数回归函数
的估计
;
步骤2将步骤1中得到的
代入式(3)中的,得到第m个模型下
的条件分位数
的估计值
;
步骤3该步将进行可变权重向量的求解,具体步骤如下:
步骤3.1将式(7)计算的结果代入式(6)中可以得到条件分位数的Jackknife估计量
;
步骤3.2将步骤3.1中的
值代入到
可得第m个模型下
的条件分位数
的Jackknife估计量
;
步骤3.3将步骤3.2中的结果代入到式(8),注意到,式(8)为关于样本t和权重
的函数,一个样本t对应一个权重向量;
步骤3.4对步骤3.3中的函数按照式(9)的原则进行非线性最优化求解则可得到的权重估计值
;
步骤4将步骤3.4中得到的权重估计值
带入到式(10)中可到的
的条件分位数
的最终估计值
。
3. 蒙特卡洛模拟
3.1. 数据生成
在本节中,首先通过数值模拟生成一系列数据来对本文所提出的CVQJMA估计量的表现效果进行评估。考虑如下几种数据产生过程:
数据1 (变系数,同方差):
样本数据
来自模型
其中
,其中
服从均匀分布
,
独立同分布于自由度为6的标准t分布。
,其中c被用来控制自变量信息占总信息的比例,即模型决定系数
,其中
在0.1至0.9之间变化。随机误差项
服从t(5)分布,且与
相互独立。
数据2 (时变,同方差):
样本数据
来自模型
其中
,随机误差项
独立同分布于标准Cauchy(0,1)分布且与
相互独立。其余数据生成方式同数据1相同。注意到,与数据1不同,此时模型中的回归系数随着观测时刻t的变化而变化。
数据3 (时变,异方差):
数据生成方式同数据2相同,只是此时随机误差项
,其中
服从标准正态分布N(0,1)分布且与
相互独立。注意到,与数据1,2不同,此时模型具有异方差性。
考虑样本数量T = 50,100,200,重复抽样次数N = 200。候选模型个数的选取参考文献 [8] 的标准,即
。为了方便起见,候选模型只考虑嵌套模型,即第m个候选模型中依次选取
中的前1~km个自变量。
3.2. 评价标准
在本节中,将要对本文所提的估计方法进行评价。具体分为以下两种情形:
情形一(可变权重选择方法评价):本文所提的CVQJMA方法基于2.2节中描述的Jackknife方法来选择权重,该方法选择的权重可以根据协变量
的取值变化而变化,是一种自适应的可变权重选择方法。为比较这种权重选择方法,本节将利用文献中固定权重下已有的分位数回归模型平均方法QJMA [11] ,QSAIC,QSBIC来进行比较。其中QSAIC权重的计算方法为
,
,
QSBIC的权重计算公式为
,
,
其中
为第m个候选模型对应的估计,计算公式见式(3)。
为比较不同权重选择方法的表现效果,定义分位数损失函数QL (Quantile Loss)为:对第r次抽样来说,
其中
,
。和文献 [5] 中的处理方式一样,最终选取的评价标准为
,
其中
,
是基于最优的候选模型计算出的估计量。
取值越小,模型权重选择方法越好。
情形二(分位数模型平均稳健性评价):为了比较分位数回归模型平均方法相对于均值回归模型平均的稳健性,将本文所提方法CVQJMA同TVQJMA [12] ,JMA [8] 和QJMA [11] 三种方法进行比较。需要说明的是,TVQJMA [12] 和JMA [8] 是基于均值回归模型平均方法,而CVQJMA和QJMA [11] 方法是基于分位数回归的模型平均方法;TVQJMA [12] 和CVQJMA是采用可变权重选择方法,而JMA [8] 和QJMA [11] 采用固定权重方法;四种模型平均方法中的权重选择方法均是基于Jackknife方法给出的。为公平起见,这里分位数回归的分位水平
取为0.5。采取的评价标准为MSE (Mean Square Error)和MAE (Mean Absolute Error),
,
,
其中
和
分别表示第t个样本下的预测值和实际值。MSE和MAE越小,预测方法越好。
3.3. 模拟结果
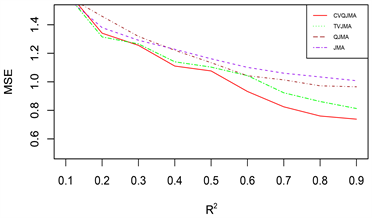
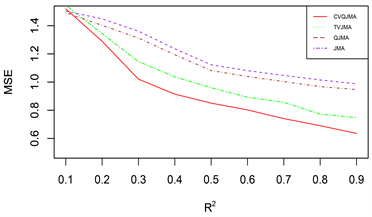
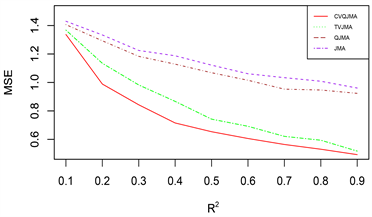
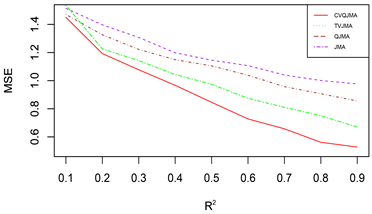
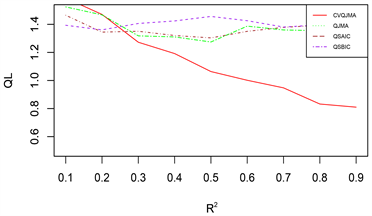
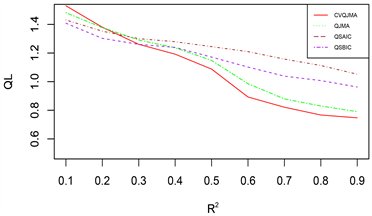
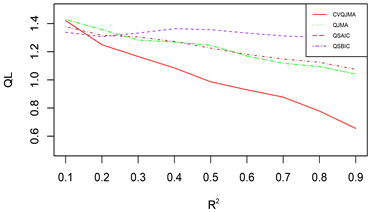
由于篇幅原因,本文只展示部分模拟结果,其余结果和展示的模拟结果类似。图1展示的是对数据1 (变系数,同方差)采用情形二(分位数模型平均稳健性评价)的评价标准的模拟结果,图2展示的是对数据2 (时变,同方差)采用情形二(分位数模型平均稳健性评价)的评价标准的模拟结果,图3展示的是对数据3 (时变,异方差)采用情形一(可变权重选择方法评价)的评价标准的模拟结果。
图中结果表明:
(1) 从预测效果来看,纵向比较可知,随着R2的增大,利用本文所提估计量进行组合预测的结果明显优于单个最优子模型预测结果;
(2) 从权重选择方法来看,本文所提可变权重的预测结果也明显优于固定权重的预测效果。此外,当
时,QJMA的表现效果和QSAIC的表现效果不分上下,QSBIC的表现效果最差;当
时,可以看出,Jackknife权重选取方法表现效果明显优于其他方法,QSBIC次之。
(3) 从回归方法的稳健性来看,分位数回归的稳健性要明显优于均值回归。
总之,综合上述几个方面来看,本文所提倡的权重选择方法有着较好的预测精度和优良的稳健性。

n = 50, M = 11, τ = 0.5 n = 50, M = 11, τ = 0.5

 n = 100, M = 14, τ = 0.5 n = 100, M = 14, τ = 0.5
n = 100, M = 14, τ = 0.5 n = 100, M = 14, τ = 0.5
 n = 200, M = 18, τ = 0.5 n = 200, M = 18, τ = 0.5
n = 200, M = 18, τ = 0.5 n = 200, M = 18, τ = 0.5
Figure 1. DGP 1 (Variable Coefficient, Homoskedasticity), Situation 2 (Quantile Model Averaging Robustness Evaluation)
图1. 数据1 (变系数,同方差),情形二(分位数模型平均稳健性评价)


n = 50, M = 11, τ = 0.5 n = 50, M = 11, τ = 0.5

 n = 100, M = 14, τ = 0.5 n = 100, M = 14, τ = 0.5
n = 100, M = 14, τ = 0.5 n = 100, M = 14, τ = 0.5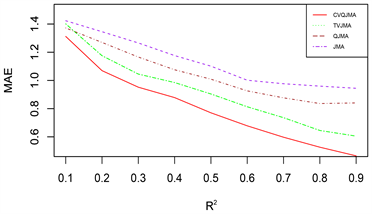
 n = 200, M = 18, τ = 0.5 n = 200, M = 18, τ = 0.5
n = 200, M = 18, τ = 0.5 n = 200, M = 18, τ = 0.5
Figure 2. DGP 2 (Time-varying, Homoskedasticity), Situation 2 (Quantile Model Averaging Robustness Evaluation)
图2. 数据2 (时变,同方差),情形二(分位数模型平均稳健性评价)
n = 50, M = 11, τ = 0.1 n = 50, M = 11, τ = 0.5
 n = 100, M = 14, τ = 0.1 n = 100, M = 14, τ = 0.5
n = 100, M = 14, τ = 0.1 n = 100, M = 14, τ = 0.5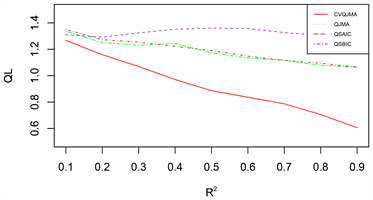
 n = 200, M = 18, τ = 0.1 n = 200, M = 18, τ = 0.5
n = 200, M = 18, τ = 0.1 n = 200, M = 18, τ = 0.5
Figure 3. DGP 3 (Time-varying, Heteroscedasticity), Situation 1 (Variable Weight Selection Method Evaluation)
图3. 数据3 (时变,异方差),情形一(可变权重选择方法评价)
4. 实证分析
4.1. 数据及变量说明
本节利用Boston房价数据对本文所提出的预测方法进行实证分析。该数据集可通过Kaggle大数据平台获取。该数据包含了Boston地区在1970年人口普查收集到的506组房价信息,共有14个变量,本文选取其中的10个连续变量,并将业主自用房子价格的中位数(MEDV)作为被解释变量Y,将地区较低地位人群占总体的百分比(LSTAT)作为协变量U,将剩余变量作为解释变量。参考文献 [13] 中的处理方式,将U进行根号开方处理,将剩余解释变量进行标准化处理。将除协变量U之外的的解释变量按照与被解释变量Y的相关性大小由高到低记为
。同时,将与被解释变量Y相关性较高的解释变量依次优先加入到候选模型中。表1给出了各变量的具体解释。

Table 1. The explanation of the variables of the Boston house price dataset
表1. Boston房价数据集变量的解释说明
4.2. 预测评估
本文将收集到的506个样本数据分为训练集和测试集两个部分,其中训练集样本数T1分别取300和400,对应剩余的样本数据作为测试集就被用来进行样本外预测精度评估。在本节中,对于CVQJMA,QJMA,QSAIC和QSBIC这四种方法,参考文献 [14] 中评价标准,采取样本外
作为预测精度的度量,其定义如下:
其中
分别取0.1和0.5分位数,
为
的预测值,
是训练集样本中被解释变量
的平均值。
度量了平方误差预测风险的相对差异,
越大,预测风险越小,预测效果越好。
对于CVQJMA,TVJMA,QJMA和JMA这四种方法,还可以考虑另外一种预测风险测量指标即均方预测误差(MSPE),其定义如下
此时,基于分位数回归的模型平均方法CVQJMA和QJMA中,分位水平
统一选取0.5。MSPE的值越小代表预测效果越好。表2和表3分别展示了不同方法下的 值和MSPE值。
4.3. 实证结果

Table 2. R ˜ 2 for different methods
表2. 不同方法下的
值

Table 3. MSPE for different methods
表3. 不同方法下的MSPE值
5. 总结
本文基于变系数分位数回归模型和模型平均方法,提出一种可变权重的分位数回归模型平均方法。相对于传统的固定权重的模型平均方法来说,该方法的候选模型权重可以随着某个协变量的变化而自适应的变化,数值模拟和实际数据分析证明了该方法具有更高的预测精度。