1. 引言
量子博弈论结合了量子力学和博弈论的思想,为我们探索决策和策略选择提供了全新的视角。在追求相对利润最大化的商业环境中,非线性成本是一个重要考虑因素。传统的经典博弈论在处理非线性成本时存在局限性,而量子博弈论通过引入量子策略,考虑了企业决策时的叠加纠缠,提供了更准确和优化的模型。而关于量子博弈论的动力学分析提供了一种更精细的策略演化模型,帮助我们更好地理解和预测博弈中的动态变化。
Elsadany [1] 和Peng [2] 等分别考虑了基于相对利润最大化下的经典博弈模型。Meyer [3] 和Eisert等 [4] 研究了在量子域中的博弈,随后Frackiewicz根据量子理论定义了Frąckiewicz (FRA)量子化方案 [5] 。Shi [6] 等应用FRA量子化方案研究了具有等弹性需求函数的量子Stackelberg双寡头博弈,李卉 [7] 等将量子纠缠引入到连续策略空间的经典古诺寡头博弈中,提出了Li-Du-Massar (LDM)量子化方案,Shi等应用LDM和FRA量子方案,研究了具有等弹性需求函数和不等边际成本的量子古诺双头博弈,并将两个量子古诺双寡头博弈与经典古诺双垄断博弈进行了比较 [8] ,朱唯唯 [9] 以及张新立等 [10] [11] [12] [13] 考虑了更多在量子空间下的博弈模型。更多关于博弈模型的研究,见文献 [14] [15] [16] 。
在现有的研究中,成本函数多采用线性成本函数,采用的量子化策略也多为LDM量子化方案,并且研究的模型大多为静态模型,不能反应正常的市场情况。同时,如果将绝对利润作为研究对象,那么不能很好的揭示企业在市场中相较于其他企业的优势与劣势。本文通过将FRA量子化方案引入具有非线性成本的经典博弈模型,建立了基于相对利润最大化的量子博弈模型,并在静态博弈模型的基础上引入有限理性调节机制建立了动态博弈模型,最后,通过理论分析以及数值模拟的方法研究了系统的动力学行为。
2. 模型建立
考虑在双寡头博弈中,2家企业采用不同的产量决策进行生产。令
以及
表示企业1和2在t周期内的产量。假设企业的逆需求函数为
,
其中
表示两家企业的总产量,常量
表示商品价格为0时的市场需求量。关于每个企业的产量采用如下的二次成本函数
,
其中
表示成本系数,根据上面所叙述的逆需求函数和成本函数,公司的绝对利润函数可以表示如下形式
(1)
企业的相对利润被定义为其绝对利润与其他企业绝对利润的差值,用
表示第一个企业的相对利润,
表示第二个企业的相对利润,根据(1)式,两个企业的相对利润函数可以由(2)给出:
(2)
根据Frackiewicz [5] 所介绍的FRA量子化方案,建立具有二次成本函数的量子古诺双寡头博弈模型。经过量子纠缠的作用,两家企业的产量纠缠在一起,并用下式表示:
(3)
其中,
和
分别代表企业1和企业2在市场中所采取的产量决策。将(3)式中
以及
代入(2)式,得到两家企业的量子相对利润为:
(4)
将(4)式中关于企业1和企业2的相对利润函数分别对
,
分别求偏导,可以得到两家企业的相对边际利润为
在实际情况中,每家企业不可能掌握市场中产生的全部信息,从而不可能完全无误的做出预测,每家企业只能对边际利润做出反应,从而做出相关调整。下面采用基于有限理性的调节机制
其中
,
分别表示第一个企业和第二个企业的产量调节速度。根据
的大小以及符号不同,企业来决定下一个时期的生产情况。从而可以得到如下的动态系统
(5)
3. 平衡点的稳定性分析
通过令
,
,可以得到系统的四个平衡点,即
,
,
以及
,其中
,
均衡点
,
,
叫做量子边界均衡点,均衡点
称为量子纳什均衡点。因为纳什均衡表示企业的均衡产量,需要有经济学上的意义,所以下面的分析和讨论是基于均衡点的值都大于0的情况。也就是需要满足条件(6)。
(6)
边界均衡点所表示的情况,为在市场中的一家或者两家企业停止了生产行为,研究这种情况没有意义,而由于在纳什均衡点
表达的含义是两家企业的产量都不为0,这更能表示实际情况中发生的情况,所以之后研究系统在
处的局部稳定性。系统在
处的雅可比矩阵为
其中
为了便于分析以及展示,引入符号
,其中
代入后得到(7)式
(7)
雅可比矩阵
在
处的特征方程是
,其中
为雅可比矩阵
的迹,
为雅可比矩阵
的行列式,分别为:
根据非线性动力学的相关理论,可以用对应量子均衡点处的雅可比矩阵特征值的模与常数1的关系来分析该均衡点的局部稳定性。当
,
,此时量子均衡点是一个稳定的结点,当
,
,此时量子均衡点是一个不稳定的结点,若
,
或者
,
,此时量子均衡点是一个鞍点。而矩阵
的特征值的表达式难以求解。根据Jury判据,当
成立时,
的所有特征值满足
,此时
是局部稳定的。将
进行简化得到(8)式:
(8)
将矩阵的迹与行列式的表达式代入之后,得到在满足(9)时,纳什均衡点
具有局部稳定性
(9)
4. 数值模拟
固定参数
以及初始条件,并选择调整速度
作为系统的分岔参数,通过使用双层迭代算法生成的双参数分岔图,我们能够展示系统的动态演变。图中的不同颜色代表不同的周期,而颜色条在图的右侧提供了相应颜色的解释。由于颜色数量的限制,黑色区域表示系统进入周期大于30的周期、逆周期、混沌或逃逸状态。从图1中我们可以观察到,当产量调节速率较低时,系统呈现出相对稳定的状态。进一步放大图1(a)得到图1(b),可以清晰地看到系统通过flip分岔或Neimark-Sacker分岔两条路径进入混沌状态。双参数分岔图提供了深入了解系统行为的视角,揭示了在不同参数取值下系统的稳定性和混沌性质。
固定参数
,图2(a)给出了关于调整速率
的1-D分岔图,蓝色和红色分别表示企业1和企业2的量子决策。当
,系统处于稳定状态,当
继续增加之后,将会出现第一次flip分岔,随后进入2周期状态,当
增加到0.423时,发生第二次flip分岔,进入4周期状态。当
时,发生第三次flip分岔,进入8周期状态,之后当
继续增加之后,系统将进入混沌状态。
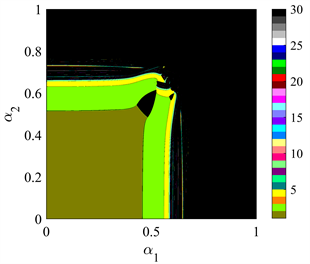
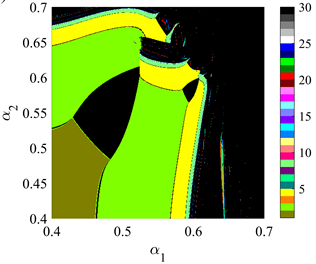 (a) 关于
,
的双参数分岔图 (b) 关于(a)的局部放大图
(a) 关于
,
的双参数分岔图 (b) 关于(a)的局部放大图
Figure 1. Two-dimensional bifurcation diagram about adjustment rates
and
图1. 关于调整速率
和
的二维分岔图
将参数固定为
,利用单参数分岔图,描述吸引子的演化过程。蓝色表示第一个公司,红色表示第二个公司。如图2(b)所示,当
时,均衡点是局部稳定的,当
等于0.567时,发生了Neimark-Sacker分岔,使得均衡点失去了稳定性,当
超过了0.567时,出现了一个不变环,并且随着
的增大,不变环的大小也随之增大。随后当
增加到0.661时,不变环坍塌为一个2周期点,随后在0.763处,发生了第一次flip分岔,2周期点变为4周期点,在
处,经历了第二次flip分岔,变为8周期点,当
进一步增大时,系统表现出混沌行为。当Neimark-Sacker分叉发生时,市场的动态突然变得准周期性,这给具有有限理性的企业带来了更大的挑战。而准周期轨迹的时间序列解有时很难与混沌状态或随机状态进行区分。这使得参与者在市场中的决策变得更加困难,因为他们需要面对一种似乎没有明确规律的行为。
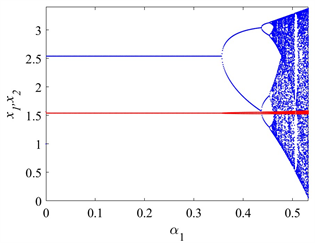
 (a) 关于
的单参数分岔图 (b) 关于
的单参数分岔图
(a) 关于
的单参数分岔图 (b) 关于
的单参数分岔图
Figure 2. D bifurcation diagram of the adjustment rate
when other parameters are fixed
图2. 固定其他参数时,关于调整速率
的一维分岔图
图3展示了量子纳什均衡点在
平面内稳定区域的边界曲线,当固定参数
时,随着纠缠参数
的增大,量子均衡点的稳定性区域将会增大。这种现象表明,当量子纠缠参数增大时,可以使市场和企业变得更稳定。这是因为纠缠参数的增加会导致企业之间的纠缠程度加深,使相关的量子系统之间的关联性更强。这种增强的关联性可以帮助企业更好地理解市场动态,提高决策的可预测性。因为纠缠现象本身具有一定的规律性,市场中的企业可以更准确地预测其他企业的行为或市场的未来走势,从而减少市场的不确定性。
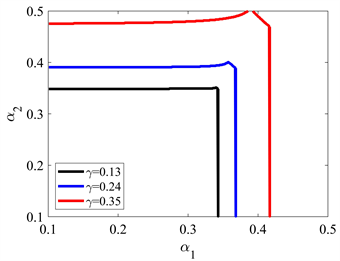
Figure 3. Different quantum entanglements correspond to the boundary curves of the stable domain of the system
图3. 不同量子纠缠对应系统稳定域的边界曲线
固定参数
,图4展示了关于参数
的单参数分岔图以及相对应的最大Lyapunov指数图,从图中可以发现,当纠缠系数
增大之后,产量调整速度对市场的灵敏度减小,这意味着产量的变动对市场影响较小。随着纠缠度的增加,系统的稳定性提高,分岔和混沌的风险降低。在图4(b)和图4(d)中的最大Lyapunov指数图的观察验证了这一点。最大Lyapunov指数为负表示系统保持稳定状态,为零表示系统处于分岔状态,而为正表示系统进入混沌状态。在这种情况下,企业之间的量子纳什均衡产量可能会下降。这是因为增加的纠缠度导致企业之间的相互影响更为复杂和强烈,从而对均衡产量产生负面影响。需要指出,纠缠度对系统稳定性和均衡产量的影响是受其他因素综合影响的,它既能提高系统稳定性,减少分岔和混沌的风险,也可能在某些情况下导致均衡产量的下降。这种复杂性需要我们在研究中综合考虑各种因素,具体情况具体分析。
综上所述,纠缠度的增加会导致系统稳定性提高,减少分岔和混沌的可能性,但可能对企业之间的量子纳什均衡产量产生负面影响,这是受纠缠度和其他因素的综合影响。

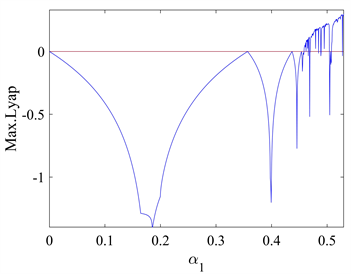 (a) 固定其他参数,
时的单参图 (b) 对应于图(a)的最大Lyapunov指数图
(a) 固定其他参数,
时的单参图 (b) 对应于图(a)的最大Lyapunov指数图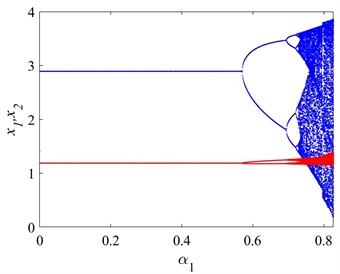
 (c) 固定其他参数,
时的单参图 (d) 对应于图(c)的最大Lyapunov指数图
(c) 固定其他参数,
时的单参图 (d) 对应于图(c)的最大Lyapunov指数图
Figure 4. The impact of the degree of entanglement on the system
图4. 纠缠程度对系统的影响
对初始条件的敏感性也是混沌行为的特征之一。固定参数
以及
。图5和图6展示了对初始条件的敏感性与量子纠缠之间的关系。对于
和
分别选取初始值
和
。其中初值为
的情况用蓝色表示,初值为
用红色表示。在图5(a)中,每个时间序列变量的两个轨道在一开始是不可区分的,它们之间的差异在18次迭代左右后迅速增加。但在图5(b)中,它们之间在24次迭代左右时迅速增加。很明显,随着量子纠缠的增加,每个变量的两条轨道之间的差异出现的更晚了。
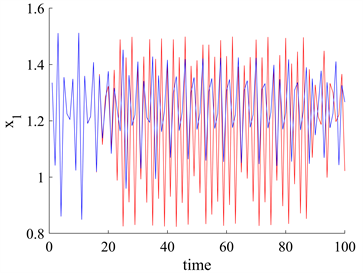
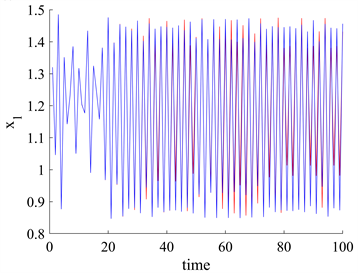 (a) 固定其他参数,
时的关于
时间序列图 (b) 固定其他参数,
时关于
的时间序列图
(a) 固定其他参数,
时的关于
时间序列图 (b) 固定其他参数,
时关于
的时间序列图
Figure 5. Sensitive dependence of
on the initial conditions of the system
图5.
对系统初始条件的敏感依赖性
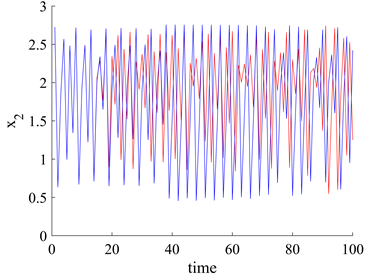
对于第二个公司,对于不同的
,图6(a)中的两个轨道会在13次迭代左右后表现出不同。在图6(b)中,在32次迭代左右时,两个轨道的差异会迅速增加。我们可以得到与前面相似的结论。经过上述的说明以及分析,可以得知,更大的量子纠缠将降低对初始条件的敏感依赖性。
当系统的初始条件发生改变时,系统的轨迹可能从一个吸引子切换到另一个吸引子,展现出不同的稳定性行为。这种现象导致吸引子共存,表现出系统多样化的演化模式。这对于理解系统的复杂性和非线性特性至关重要,因为它意味着相同的系统在不同的初始条件下可能展示出截然不同的演化行为。有助于更好地理解和控制复杂系统的行为。
 (a) 固定其他参数,
时的关于
时间序列图 (b) 固定其他参数,
时的关于
时间序列图
(a) 固定其他参数,
时的关于
时间序列图 (b) 固定其他参数,
时的关于
时间序列图
Figure 6. Sensitive dependence of
on the initial conditions of the system
图6.
对系统初始条件的敏感依赖性
固定参数
,图7(b)表明,当
时,初值取在绿色区域中时,产生的轨迹会收敛于黑色不变环,而当初值取在黄色区域中时,产生的轨迹会收敛于红色2周期吸引子,蓝色区域为逃逸区域。随着
的进一步增加,绿色吸引盆面积逐渐变小,黄色吸引盆面积逐渐增大。最后黑色不变环与其吸引盆边界发生接触,发生接触分岔,黑色不变环消失。在经济学和市场研究领域,吸引子共存现象被用来阐释不同竞争策略的协同存在以及彼此之间的相互作用。在市场竞争背景下,企业可以采用各种策略,例如生产产量竞争、产品特色差异化,或专注于特定市场细分。这些多样的竞争策略可以被视为不同的吸引子,它们在市场上共同存在,并相互影响。这种现象有助于解释市场中多样性和竞争策略的动态,为理解企业行为和市场发展提供了重要的洞察。
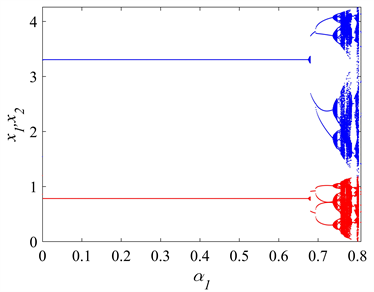
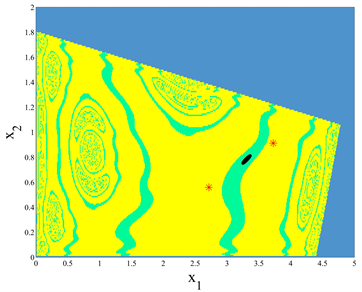 (a) 单参数分岔图 (b) 吸引盆
(a) 单参数分岔图 (b) 吸引盆
Figure 7. Coexistence attractor and its attraction basin
图7. 共存吸引子及其吸引盆
5. 总结
针对现有对寡头博弈中的研究存在的成本函数多为线性成本函数,量子化策略较为单一,模型大多为静态模型以及研究对象多为绝对利润的现状,本文将FRA量子化策略引入具有非线性成本函数的古诺寡头博弈中,并以相对利润作为研究对象,之后以有限理性调节机制建立了动态博弈模型,之后对模型进行分析,在其中发现了丰富的动力学现象,发现当企业以较小的调整速率对市场进行调节时,市场环境将会保持相对稳定。同时,纠缠参数的增加会降低系统的初值敏感性。以及系统将会通过何种路径进入混沌。这些研究为后续企业控制市场环境的稳定提供了理论依据。当将纠缠参数控制在一个合适的区间时,会创造出更稳定的市场环境。也同时可以为企业带来更大的收益。而在更加复杂的市场环境中,企业不仅仅会受到内部条件的干扰,可能会受到来自外部的影响。基于这些考虑,根据具体的条件,今后可以对系统进行进一步的修正与改进。