1. 引言
由量子叠加产生的量子相干性是量子力学中最重要的特征之一,也是量子物理学和经典物理学的区别之一。量子相干性在量子光学 [1] 、量子计量学 [2] 、量子信息处理 [3] 、纳米科学 [4] 等方面有着十分重要的应用。随着对量子相干性的更加深入研究,Baumgratz等人通过类比量子纠缠资源理论提出了量子相干性的资源理论 [5] ,并且提出了能够刻画量子相干性的相干度量应该满足的约束条件。在此之后越来越多满足这些约束条件的相干度量被提出,例如:迹距离相干度量 [6] 、Tsallis α相对熵相干度量 [7] 、相对熵相干度量 [5] 、
范数相干度量 [5] 、基于Hellinger距离相干度量 [8] 。利用这些相干度量能够更好的去研究量子相干和量子关联的关系 [9] 等更多量子相干的性质。
相互无偏基(Mutually unbiased bases)是Hilbert空间中十分特殊的一类基,它最初被发现于对量子态的测量。作为确定量子态的最佳测量基 [10] 它在量子误差校正 [11] 、量子态层析成像 [12] 、量子纠缠检测 [13] 等方面有着十分重要的作用。在d维量子系统中若d可以表示为一个素数幂则这个量子系统上最多可以构造
组相互无偏基 [10] ,更多维数的最大相互无偏基的个数和构造方法仍然是众多学者研究的课题。
本文主要研究在三维和四维相互无偏基下对于特殊的三维X态和四维Bell对角态在基于Hellinger距离相干度量下的量子相干性,在此基础上讨论在不同的相互无偏基下相干性之间的关系。
2. 三维相互无偏基下X态基于Hellinger距离的相干性
在固定参考基下
下,量子态
的基于Hellinger距离的相干度量被定义为:
(1)
其中
是量子态
和
的Hellinger距离。
若
是d维Hilbert空间
上的一组相互无偏基当且仅当
其中
。在
中相互无偏基的最大数目是四组,分别为:
其中
。
接下来研究在三维空间
中的相互无偏基
下X态基于Hellinger距离的相干性。三维X态可以用密度矩阵表示为
通过计算可以求得量子态
的特征值如下
其对应的特征向量分别是
当参考基为
时可以得到
基于Hellinger距离的相干性
(2)
其中
。同样的可以求出当参考基为
时
基于Hellinger距离的相干性
(3)
接下来我们令
其中
都是实数,通过以上方法可以得出
,
,并且在参考基
下态
和态
的基于Hellinger距离的相干性也都是相等的。
3. 四维相互无偏基下Bell对角态基于Hellinger距离的相干性
Bell对角态在量子信息中扮演着重要的角色,尤其在量子相干性的估计上有极其重要的应用 [14] 。两量子比特X态表示为
(4)
其中
为泡利矩阵
,
为Bloch向量,若
就可以得到两量子比特的Bell对角态,
其中
,
。在
中最大相互无偏基的个数为五组,分别为:
(5)
在参考基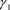 下
基于Hellinger距离的相干性
下
基于Hellinger距离的相干性
(6)
其中
。同理可得在参考基
下
基于Hellinger距离的相干性
根据以上求得的结果还可以得到
在
下基于Hellinger距离的相干性的和
. (7)
在图1中我们绘制了
关于变量
的三维图形,其中(a):
;(b):
;(c):
。

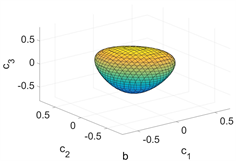
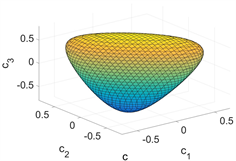
Figure 1. Surfaces of constant
图1.
等于不同常数的曲面图
设
是一组相互无偏基,若
其中
,则
被称为autotensor of mutually unbiased basis (AMUB)。在四维相互正交基
中
为AMUB [15] 。通过对
表达式的比较可以发现:设
则
,
,
。
4. 总结
在本文中,我们研究了在相互无偏基下的基于Hellinger距离的量子相干性。对于三维最大相互无偏基
,我们发现了三维X态对于其中不同的三组参考基
能得到相同的基于Hellinger距离的相干性。对于四维最大相互无偏基
,对于其中三组AMUB
可以发现基于这三组基求得的基于Hellinger距离的相干性可以通过对
相互置换互相表示出来,并且在剩余的两组参考基
下的Hellinger距离的相干性是相等的关系。
参考文献