1. 背景
在人类感知世界并获取信息的诸多手段之中,视觉毫无疑问是其中最为重要的一个部分。现代医学的相关研究显示,人类的视觉皮层约由1亿4000万个神经元所构成,是人类大脑中最为神秘的部分之一。这些神经元主要负责处理与解释人眼所接收到的视觉数据,从而提供相应的感知信息并形成记忆。即便观察到的只是一些稀少甚至模糊的视觉信息,人类也能够从中提取出大量的内容。 [1]
作为一个典型的复杂交叉学科研究领域,计算机视觉实际上包含了来自计算机科学,数学,物理学,生物学与心理学等方面的诸多技术。从抽象的角度而言是计算机视觉中最为经典也最为关键的任务之一。
考虑到人对图像内容的感知方式与计算机处理并理解图像过程之间的碁异,因此图像分类模型的重要性不會而喻,它是决定图像分类性能的关键所在图像分类模型中的特征提取主要是实现对图像特征信息的量化,将图像中的抽象内容转化为计算机可以处理的数学对象(例如由数字组成的向量或矩阵),而图像分类模型中的分类算法则是应用机器学习领域中的相关知识来对这些数学对象进行计算与分析的方法。截至目前为止,人们对高效而鲁棒的图像分类模型开展了广泛的研究并取得了很多成就与突破。但由于图像与生俱来的复杂性,我们在这一方面仍然还有很多问题亟待解决。图像的复杂性在很大程度上是由于图像中对象的各种变化因素造成的,这些变化因素主要包括:
(1) 视角变化;(2) 缩放变化;(3) 形变变化;(4) 遮挡变化;(5) 光照变化。
在现实中,图像分类不仅需要处理上述变化因素中的某一类情况,还往往面临着多种变化因素的联合挑战,因此对于能够有效处理各种复杂图像变化的图像分类模型进行研究将会具有广阔的应用前景与可观的经济价值。由于图像分类是其他更为复杂的计算机视觉任务的基础,它的应用范围早己遍布全球各个角落。
2. 研究现状
在传统的图像分类中,图像特征的处理与分类算法的实现通常都是遵循欧氏空间几何来进行的。以人脸识别为例,早期的方法将人脸的灰度图像转化为特征向量,然后使这样的做法在面对存在视角变化与光照变化的人脸图像时很难获得正确的分类结果(相近位置的像素灰度值变化很大)。
随着相关研究的不断开展,协方差矩阵在图像分类问题中的优点开始得到重视。最初,Tuzel等人 [2] 首先提出使用协方差矩阵来对图像特征进行计算与表示。此时的协方差矩阵相当于图像的一种区域描述符,可以通过积分图像进行快速计算。由于协方差矩阵并不处于欧氏空间中,因此他们使用基于广义特征值的距离度量来对其进行计算。Pang等人 [3] 随后就将协方差矩阵应用在人脸图像识别中,他们以图像像素的位置信息与Gabor滤波特征来计算图像的区域描述符,实现了两种不同类型信息在协方差矩阵中的融合,并在实验中证明了该方法的优点。对称正定矩阵流形上的核方法也为稀疏表示的应用提供了诸多便利,Hamndi等人就 [4] 利用基于矩阵散度的核函数来将对称正定矩阵流形嵌入到核空间中进行稀疏表示,他们还基于这样的核函数实现了黎曼流形上的字典学习。
近年来,基于黎曼流形的分类算法的研究热度不断上升,不断在之前的算法基础上融入黎曼流形对之前的传统算法进行优化,本文在传统的SVM的集成学习上加入了基于黎曼流形的核函数,并使用经典的RFE算法进行特征的筛选提高模型的计算速度,使模型具有更好的分类效果和鲁棒性。
3. 理论基础
3.1. 黎曼流形与对称正定矩阵流形
从最单纯的角度来说,黎曼流形是数学中的一个概念,定义了一类有着局部近似于欧氏空间特性的平滑弯曲空间。虽然黎曼流形的概念较为抽象,但实际上我们的日常生活中就存在常见的黎曼流形实例,比如地球。
一个大小为
的实数矩阵
是一个对称正定矩阵,当且仅当X对任意的非零向量
;都满足
。这样的n维对称正定矩阵所在的空间形成的一个具有李群(Lie Group)结构的黎曼流形即为对称正定矩阵流形(记为
),这一流形可以方便的应用微分流形上的各种概念。对于任意一点
,其切空间
为n维对称矩阵集合:
此时黎曼流形上的指数映射与对数映射在对称正定矩阵流形上则转化为矩阵的指数运算与对数运
算。令
为一个对称正定矩阵X的特征值分解,则X的对数可通过下式计算:
其中
为对矩阵
中的每个对角线元素进行对数运算。由于一个对称正定矩阵的特征值均为正数,因此以上操作是可行的。类似的,令
为对称矩阵
的特征值分解,则
的指数可通过下式计算:
其中
为对D中每个对角线元素进行指数运算,
为一个对称正定矩阵。
对数欧氏度量(Log-Euclidean Metric, LEM)是对称正矩阵流形上的另一种常用距离度量,其本质是欧氏距离在对称正定矩阵流形对数域中的扩展。由对数欧氏度量定义的距离
可通过下式计算:
这里对数欧氏度量实际上通过对数映射
将对称正定矩阵映射到了n维单位矩阵
的切空间中(即n维对称矩阵空间
),因此其距离计算就简化为
中的欧氏距离。相比仿射不变度量,对数欧氏度量简洁易用并便于计算。
3.2. 多核学习
SVM是机器学习里面最强大最好用的工具之一,它试图在特征空间里寻找一个超平面,以最小的错分率把正负样本分开。它的强大之处还在于,当样本在原特征空间中线性不可分,即找不到一个足够好的超平面时,可以利用核(kernel)函数,将特征映射到希尔伯特(Hilbert)空间。后者一般维度更高,通过这样的映射之后,样本在新的特征空间中便是线性可分的了。
我们通过核把特征从低维空间映射到高维空间。举例来说,我们看下面的多项式核函数:
其中
是两个样本,他们的特征分别是
,
,通过这个核函数,可以看到二维特征被映射到了六维特征。而且我们也可以理解,这个映射其实就是用一个矩阵A乘以原来的特征
得到的。矩阵A也就是核矩阵了。一个核函数对应一个核矩阵。
多核学习(Multiple Kernel Learning, MKL)是一种机器学习方法,它利用多个不同的核函数来学习模型,从而提高模型的性能和泛化能力。核函数是一种用于非线性分类和回归的工具,它可以将非线性特征空间映射到高维空间中,从而使得原本线性不可分的数据在高维空间中变得线性可分。
传统的核方法是使用单个核函数,但是单个核函数可能无法适应复杂的数据分布,从而导致模型的性能下降。多核学习通过将多个核函数进行组合来学习模型,从而可以更好的适应不同的数据分布。多核学习的基本思想是将多个核函数进行加权组合,从而构建一个更加通用的核函数。这个加权组合的过程可以通过优化一个目标函数来实现,通常会使用正则化方法来控制核函数的复杂度。
本文使用的多核学习组合思路是在传统的多核学习上加入一个基于黎曼流形的预先计算核。
3.3. 特征筛选SVM-RFE
SVM [5] 的主要思路是寻找一个最优分类超平面,使得两类数据之间的间隔最大,亦称为间隔最大化原理。根据SVM这一原理及特征选择的特点,有很多研究人员将SVM的分类和特征选择融合在一起,其中GUYON等 [6] 提出的SVM-RFE方法应用最为广泛。它将特征贡献度和支持向量机类别间隔相关联,通过删除特征造成的SVM类别间隔变动来对特征在分类贡献上的大小进行排序,利用这一特征选择标准减少并优化特征,达到获取最优特征组合的目的。具体数学表征如下。
下式为SVM优化后的分类面方程,
与
为特征矢量和标签,
是SVM核函数。
代表拉格朗日系数,分类间隔可表示为 [7]
。假设
含有K个特征,每个特征对于分类的贡献则可以通过删除该特征造成的分类间隔的变动大小来衡量。
SVM-RFE通过递归迭代的方式逐次删除分类贡献低的特征,完成对于所有特征按照分类贡献度大小的排序。在特征删选上,则可以通过SVM-RFE对单个图像特征矩阵,或者图像特征进行排序 [8] 。
4. RMKL-RFE算法
在切空间内,从原始黎曼空间映射过来的点都能保留对称正定矩阵之间黎曼距离的信息,而对称正定矩阵又与原始的图像数据的互协方差矩阵一一对应。于是可以利用SVM核函数的形式将原始空间中提取出来的特征数据映射到黎曼流形的切空间中,相当于间接提取了图像的流形特征,可以称之为黎曼核支持向量机算法(Riemann kernel SVM, RKSVM)。将获得的黎曼核函数与其他的多核学习常用的核函数结合进行多核学习形成一个新的多核学习方法,我们将其命名为黎曼多核学习特征选择算法(Riemann Multiple Kernel Learning RFE, RMKL-RFE),核函数的具体介绍如下。
以图像协方差矩阵为特征
在本文中,我们提出了一种核方法其将对空间协方差矩阵进行不同的操作。通过构造,空间协方差矩阵是对称的,并且如果使用了足够的数据来估计它,它也将是正定的。
这些矩阵的直接向量化没有考虑到它们之间的关系,即对称和正定(SPD)矩阵的系数。此外,矢量化的协方差矩阵不服从正态分布,使得大量流行的分类算法,如最适合高斯分布的线性判别分析(LDA),效率较低。
我们注意到
维的SPD矩阵
形成一个维数为
的可微流形M,因此,这些矩阵的正确操作依赖于微分几何的一个特殊分支,即黎曼几何 [9] 。该方法考虑了协方差矩阵空间
的黎曼几何。如图1,实际上,在每个点C(即,在我们的情况下,每个协方差矩阵),可以在相关联的切空间
中定义标量积。这个切空间是欧几里得的,并且是流形的局部同态,流形中的黎曼距离计算可以很好地近似于切空间中的欧几里得距离计算。设
和
就是两个切向量(即在我们的例子中两个对称矩阵),切空间C处的标量积可以用以下关系来定义:
此外,对数映射局部地将所有协方差矩阵
投影到切平面上。
其中
表示矩阵 [5] 的对数。可对角化矩阵
的对数定义为
,其中对角元素由
给出。此外,将切空间的元素投影回流形的逆运算,即指数映射,定义为:
表示矩阵的指数。
基于黎曼的内核:根据这些黎曼几何工具,可以将每个协方差矩阵局部投影到切平面中,并使用该新空间来操纵投影的协方差矩阵。对于流形中协方差矩阵的直接操作,参考Barachant等人 [10] 。让我们考虑标量积,其在
处的切平面中定义,并且由(3)给出。我们建议在协方差矩阵上使用以下显式映射函数:
通过结合黎曼流形上的对数映射与指数映射我们可以构建出基于黎曼流形的核矩阵称为黎曼核,这里使用
来表示黎曼核。
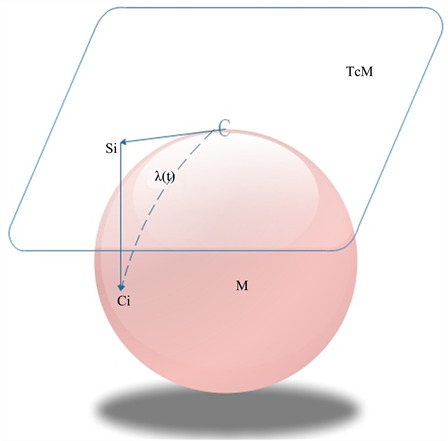
Figure 1. Schematic diagram of Riemann mapping
图1. 黎曼映射示意图
为了处理复杂的计算机视觉数据,本文引入了一种多核学习理念,通过综合损失设计将多个单独的核损失组合成一个整体,以便在相应的RKHS中同时寻找多个解,即通过最小化多个RKHS中的统一集成损失来共同优化学习最优参数。基于参数空间多核集成约束如下:
其中,L为核的个数;
为第i个
的格拉姆矩阵;
为第i个核
的权重,
;
为
的偏置项;
为
的系数;
为第i个核中第t个样本的铰链损失;
为所有分类中第t个样本损失的和。通过统一损失,得到了本文方法模型,定义如下:
其中,第1项
为统一的铰链损耗,是衡量基本核模型质量的标准;第2项
和第3项
构成共享参数空间中的组合平滑核函数;
和
均为
的列向量,指与 中每个训练数据样本的权重相关的共享参数;C为正则化参数,可控制经验损失的最小值和风险损失的最小值之间的平衡。
跟传统的多核学习方法有所区别,本文方法将黎曼核函数通过预先计算的方式,作为预先计算核,计算出黎曼核矩阵
然后进行多核集成学习,通过在传统多核学习中加入黎曼核函数,弥补了在使用流形数据进行分类时准确率低,容易误判的问题,增强了多核学习的鲁棒性,提高了准确率,由于黎曼核矩阵的计算复杂度较高,所以引入了特征选择算法对模型进行特征选择使用选择出的特征进行后续的训练与测试。
具体算法如下:
5. 数值模拟
为了验证我们的方法的有效性,我们在4个基准数据集上进行测试,他们分别应用于纹理识别、汽车品牌识别、动物皮肤识别和天气识别。
Brodatz是一个纹理数据库 [11] [12] ,在该数据集中包含240张纹理图片,随机选择216张纹理图片作为该实验的样本集。在实验中,将每张图片的尺寸调整为40 × 40,并在每张图片中选取24个采样点,以每个采样点为圆心半径为3,进行局部二进制编码。
Weather图像集是一个天气图像分类库,该数据集中包含500张天气图片,分属于四个类别分别是晴天,雨天,晚霞和多云。
ABVBN图像集是一个汽车品牌图像集,该数据包含三个相似的汽车品牌车标,共1059张图片,清晰度较低,识别难度较大。
AN skin图像集是动物皮肤图像的数据集,共包含240张动物皮肤图像。
在这四个数据集上我们与其他的一些传统方法与未优化之前的方法进行对比,例如:Linear-SVM,Gau-SVM,Poly-SVM,COV-SVM,SPDMPL以及MKL-SVM。
图2中展现的是各方法在各个图像集上的平均准确率,可以更直观的看出各个方法的准确率,本文提出的方法的准确率最高达到了90.45效果最佳,从表1中也我们可以看出几种传统的算法在各个图像集上的分类准确率都较差,本文的算法由于融入了黎曼核函数在四个图像集上的分类效果最好,基本上都达到了90以上的准确率;在ABVBN图像集上的准确率较低只有80.1,是由于该图像集中的图像清晰度较低,结构信息所含较少,对于本文算法的优势无法完全展现,但是RMKL-RFE仍然在几种算法中的准确率最高,本文所提出的算法对与准确率的提高效果显著,且有较强的鲁棒性。

Table 1. Average results of each algorithm on the dataset
表1. 各算法在数据集上的平均结果
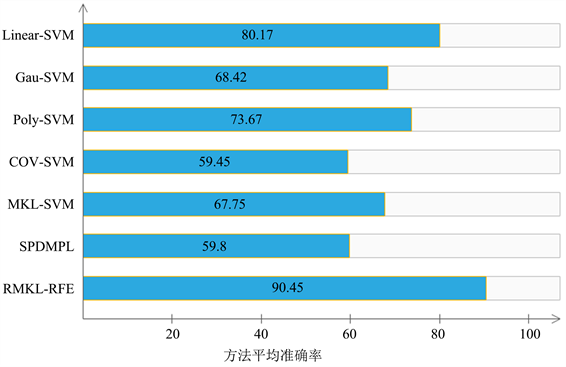
Figure 2. Average accuracy of different methods on each image set
图2. 不同方法在各图像集上的平均准确率
6. 总结
本文的目的是弥补传统SVM算法在数据的流形结构信息无法充分利用的问题,增强分类效果。与传统的算法不同,本文构建了黎曼核函数,使用多核学习的方法将黎曼核函数与其他的传统的核函数进行结合,增强了算法对于结构信息的利用程度,提高了算法的分类准确率和鲁棒性,并在此基础上加入了特征选择方法RFE算法进一步加强了算法的准确性和计算速度,但是该方法的时间复杂度仍然较大在数据量较大时仍然需要较长的时间,因此接下来我们需要对算法计算复杂度进行优化。