捕食者患病且具有分布时滞感染率的捕食–食饵模型

A Predator-Prey Model with Infected Predator and Distributional Time-Delay Infection Rates

摘要: 本文研究了捕食者患病且具有分布时滞感染率的捕食–食饵模型。文中假设疾病仅在捕食者种群中流行，易感捕食者和患病捕食者皆以食饵为唯一的食物来源。文中运用单调动力系统理论和构造Lyapunov泛函相结合的方法得到了模型中所有边界平衡点的全局稳定性，同时运用一致持久生存理论得到了患病捕食者一致持久生存的充分条件。最后，文末数值模拟的部分不仅验证了定性理论分析结果的正确性，而且就同一模型针对感染率大小不同以及疾病潜伏期长短不同的情形分别进行了敏感度分析。

Abstract: In this paper, we investigate a predator-prey model in which predators are infected and have dis-tributed time-lagged infection rates. It is assumed that the disease is endemic only in the predator population and that both susceptible and infected predator’s use prey as their only food source. The global stability of all boundary equilibrium points in the model is obtained using a combination of monotone dynamical systems theory and the construction of Lyapunov generalized functions, and a sufficient condition for the consistent persistence of the infected predator is obtained using the theory of consistent persistence. Finally, the numerical simulation section at the end of the paper not only verifies the correctness of the qualitative theoretical results, but also analyzes the sensitiv-ity of the same model to different infection rates and disease incubation periods.

1. 引言

自然生态环境中存在着形如依赖、竞争、捕食等关系。在种群生态学与种群动力学领域，捕食–食饵关系都是重要的研究对象，专家和学者们也在该课题上取得了很多成果 [1] - [7] 。因为疾病会在生物种群中传播，以至于会影响到种群的数量，从而生态传染病模型也得到了越来越多的重视与研究 [8] - [15] 。

2022年，李敏等人研究了捕食者患病的捕食–食饵模型，模型如下 [16] ：

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}x\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{y}_s\left(t\right)-x\left(t\right){\eta }_2{y}_i\left(t\right)\hfill \\ \frac{\text{d}}{\text{d}t}{y}_s\left(t\right)=k_1{\eta }_{1}x\left(t\right)y_s\left(t\right)-\beta y_s\left(t\right)y_i\left(t\right)-d_s{y}_s\left(t\right)\hfill \\ \frac{\text{d}}{\text{d}t}{y}_i\left(t\right)=k_2{\eta }_{2}x\left(t\right)y_i\left(t\right)+\beta y_s\left(t\right)y_i\left(t\right)-d_i{y}_i\left(t\right)\hfill \end{array}$ (1)

模型(1)中的参数和变量的生物意义见文献 [16] 。模型(1)中的疾病感染率采用了双线性形式的感染率，但事实上由于疾病存在潜伏期的问题，且潜伏期的长短也会因为动物的体质、年龄等有所不同，因此本文将在文献 [16] 的模型(1)的基础上，考虑疾病潜伏期时滞的生物因素，建立了一个具有分布时滞感染率的捕食–食饵模型，并通过运用单调动力系统理论和构造Lyapunov泛函相结合的方法定性的分析改进后的模型的动力学性态。

2. 模型的建立

在文献 [16] 中的模型的基础上，本文模型同样研究了两类种群：食饵种群 $x\left(t\right)$ 和捕食者种群 $P\left(t\right)$ ，针对本文模型的具体生物意义假设如下：

(1) 假设疾病仅在捕食者之间流行，从而捕食者种群可划分为易感捕食者种群 $P_s\left(t\right)$ 和患病捕食者种群 $P_i\left(t\right)$ ，捕食者种群的种群密度为 $P\left(t\right)=P_s\left(t\right)+P_i\left(t\right)$ 。

(2) 食饵种群的增长率为Logistic形式的增长率 $\stackrel{\dot{}}{x}\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)$ 。其中r为食饵种群的内禀增长率，K为环境容纳量。

(3) 假设捕食者种群中流行的疾病无垂直传播现象，患病捕食者不具备自然恢复与自然免疫的能力。 $\tau$ 是种群感染疾病后的最大潜伏期； $f\left(\xi \right)$ 是 $\left[0,\tau \right]$ 上的非负函数，并且满足 ${\displaystyle {\int }_0^{\tau }f\left(\xi \right)\text{d}s}=1$ ， ${\displaystyle {\int }_0^{\tau }\xi f\left(\xi \right)\text{d}s}<+\infty$ 。假设疾病发生率为 $\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}$ 。

(4) 易感捕食者和患病捕食者皆具有捕获食饵的能力，易感捕食者 $P_s\left(t\right)$ 和患病捕食者 $P_i\left(t\right)$ 对食饵的捕获概率 [17] 分别用 ${\eta }_1,{\eta }_2\left(0\le {\eta }_1,{\eta }_2\le 1\right)$ 表示；由于患病捕食者 $P_i\left(t\right)$ 的捕获能力弱于易感捕食者 $P_s\left(t\right)$ 的捕获能力 [18] ，故令 ${\eta }_1>{\eta }_2$ 。

(5) 食饵的自然死亡率用 $\mu$ 表示，且满足 $r-\mu >0$ 。易感捕食者和患病捕食者的死亡率分别表示为 $d_s$ 和 $d_i$ ，由于捕食者种群内有疾病传播，患病捕食者抵抗力低于易感捕食者，故令 $d_s<d_i\left(0\le d_s,d_i\le 1\right)$ ， $P_s\left(t\right)$ 和 $P_i\left(t\right)$ 捕获食饵后的营养转化率分别为 $k_1$ 和 $k_2$ ，且满足 $0<k_2\le k_1<1$ 。

基于上述假设，捕食者患病且具有分布时滞感染率的捕食–食饵模型如下：

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}x\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{P}_s\left(t\right)-x\left(t\right){\eta }_2{P}_i\left(t\right)\hfill \\ \frac{\text{d}}{\text{d}t}{P}_s\left(t\right)=k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_s{P}_s\left(t\right)\hfill \\ \frac{\text{d}}{\text{d}t}{P}_i\left(t\right)=k_2{\eta }_{2}x\left(t\right)P_i\left(t\right)+\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_i{P}_i\left(t\right)\hfill \end{array}$ (2)

3. 准备工作

考虑到生物学意义，本文仅考虑在以下正向不变集中讨论模型(2)的动力学性态：

$\Omega =\left\{\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)\in {ℝ}_{+}^3:x\left(t\right)>0,P_s\left(t\right)>0,P_i\left(t\right)>0\right\}$

模型解的正性和有界性

命题3.1模型(2)中满足初始条件 $\left(x\left(0\right),P_s\left(0\right),P_i\left(0\right)\right)$ 的解满足正性和有界性。

证明模型(2)的解的正性与文献 [19] 中模型(5)的解的正性证明过程类似，此处省略。下面主要证明本文模型(2)中解的有界性。

设模型(2)的任意解为 $\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)$ ，由：

$\frac{\text{d}x\left(t\right)}{\text{d}t}\le rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)$

可得：

$\underset{t\to +\infty }{\lim }\sup x\left(t\right)\le K$

定义：

$W\left(t\right)=x\left(t\right)+P_s\left(t\right)+P_i(\; t\; )$

从而，得到函数 $W\left(t\right)$ 沿着模型(2)的正解的全导数：

$\begin{array}{c}{W}^{\prime }\left(t\right)=x^{\prime }\left(t\right)+{P^{\prime }}_s\left(t\right)+{P^{\prime }}_i\left(t\right)\\ =rx\left(1-\frac{x}{K}\right)-\mu x\left(t\right)-\left({\eta }_1-k_1{\eta }_1\right)x\left(t\right)P_s\left(t\right)-\left({\eta }_2-k_2{\eta }_2\right)x\left(t\right)P_i\left(t\right)-d_s{P}_s\left(t\right)-d_i{P}_i\left(t\right)\\ \le rx\left(1-\frac{x}{K}\right)-\mu x\left(t\right)-d_s{P}_s\left(t\right)-d_i{P}_i(\; t\; )\end{array}$

取 $\rho =\min \left\{\mu ,d_s,d_i\right\}$ ，于是有：

$W^{\prime }\left(t\right)\le rx\left(1-\frac{x}{K}\right)-\rho (x\left(t\right)+P_s\left(t\right)+P_i(\; t\; ))$

因 $\underset{t\to \infty }{\lim }\sup x\left(t\right)\le K$ ，则假设存在正常数B和T，使得当 $t\ge T$ 时：

$W^{\prime }\left(t\right)\le B-\rho W(\; t\; )$

成立，故得：

$\underset{t\to +\infty }{\lim }\sup W\left(t\right)\le \frac{B}{\rho }$

即证得模型(2)解 $\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)$ 的一致有界性。

4. 模型(2)边界平衡点的存在性

模型(2)的平衡点 $E\left(\tilde{x},{\tilde{P}}_s,{\tilde{P}}_i\right)$ 皆满足如下方程：

$\begin{array}{l}r\tilde{x}\left(1-\frac{\tilde{x}}{K}\right)-\mu \tilde{x}-\tilde{x}{\eta }_1{\tilde{P}}_s-\tilde{x}{\eta }_2{\tilde{P}}_i=0\\ k_1{\eta }_1\tilde{x}{\tilde{P}}_s-\beta {\tilde{P}}_s{\tilde{P}}_{i}T\left(\tau \right)-d_s{\tilde{P}}_s=0\\ k_2{\eta }_2\tilde{x}{\tilde{P}}_i+\beta {\tilde{P}}_s{\tilde{P}}_{i}T\left(\tau \right)-d_i{\tilde{P}}_i=0\end{array}$

其中 $T\left(\tau \right)={\displaystyle {\int }_0^{\tau }f\left(s\right)\text{d}s}$ 。

由上述方程组可解得模型(2)存在平衡点：

$E_0=\left(0,0,0\right)$

当满足条件 $\mu <r$ 时，模型(2)存在平衡点：

$E_1=\left(K-\frac{K\mu }{r},0,0\right)$

由模型假设可知，当：

$k_2{\eta }_{2}K\left(r-\mu \right)>r{d}_i$ (3)

时，模型(2)还存在边界平衡点 $E_2$ 和 $E_3$ ：

$E_2=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K},0\right)\triangleq \left(x_2,P_2,0\right)$

$E_3=\left(\frac{d_i}{k_2{\eta }_2},0,\frac{k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i}{k_2{\eta }_2^{2}K}\right)\triangleq \left(x_3,0,P_3\right)$

模型(2)还存在正平衡点 $E_4\left(x^{*},P_s^{*},P_i^{*}\right)$ ，其中：

$x^{*}=\frac{K\left[\beta T\left(\tau \right)\left(r-\mu \right)-{\eta }_1{d}_i+{\eta }_2{d}_s\right]}{K{\eta }_1{\eta }_2\left(k_1-k_2\right)+\beta rT(\; \tau \; )}$

$P_s^{*}=\frac{1}{\beta T\left(\tau \right)}\left(\frac{K{k}_1{\eta }_1\left[\beta T\left(\tau \right)\left(r-\mu \right)-{\eta }_1{d}_i+{\eta }_2{d}_s\right]}{K{\eta }_1{\eta }_2\left(k_1-k_2\right)+\beta rT\left(\tau \right)}-d_s\right)$

$P_i^{*}=\frac{1}{\beta T\left(\tau \right)}\left(d_i-\frac{K{k}_2{\eta }_2\left[\beta T\left(\tau \right)\left(r-\mu \right)-{\eta }_1{d}_i+{\eta }_2{d}_s\right]}{K{\eta }_1{\eta }_2\left(k_1-k_2\right)+\beta rT(\; \tau \; )}\right)$

为了研究模型(2)平衡点的稳定性，需要求解模型(2)在平衡点 $E\left(\tilde{x},{\tilde{P}}_s,{\tilde{P}}_i\right)$ 处的线性近似方程，从而作变量替换 $u_1=x-\tilde{x},u_2=P_s-{\tilde{P}}_s,u_3=P_i-{\tilde{P}}_i$ ，并带入模型(2)，取其线性近似部分可得：

$\begin{array}{l}{\stackrel{\dot{}}{u}}_1=\left(r-\frac{2r\tilde{x}}{K}-\mu -{\eta }_1{\tilde{P}}_s-{\eta }_2{\tilde{P}}_i\right)u_1-\tilde{x}{\eta }_1{u}_2-\tilde{x}{\eta }_2{u}_3\\ {\stackrel{\dot{}}{u}}_2=k_1{\eta }_1{\tilde{P}}_s{u}_1+\left(k_1{\eta }_1\tilde{x}-\beta {\tilde{P}}_i-d_s\right)u_2-\beta {\tilde{P}}_s{\displaystyle {\int }_0^{\tau }f\left(s\right)u_3\left(t-s\right)\text{d}s}\\ {\stackrel{\dot{}}{u}}_3=k_2{\eta }_2{\tilde{P}}_i{u}_1+\beta {\tilde{P}}_i{u}_2+\left(k_2{\eta }_2\tilde{x}-d_i\right)u_3+\beta {\tilde{P}}_s{\displaystyle {\int }_0^{\tau }f\left(s\right)u_3\left(t-s\right)\text{d}s}\end{array}$ (4)

定理4.1由模型(4)，模型(2)在平衡点 $E_0\left(0,0,0\right)$ 处的线性化矩阵为：

$J\left(E_0\right)=\left(\begin{array}{ccc}r-\mu & 0& 0\\ 0& -d_s& 0\\ 0& 0& -d_i\end{array}\right)$

则 $J\left(E_0\right)$ 的特征方程为：

$\left(\lambda -r+\mu \right)\left(\lambda +d_s\right)\left(\lambda +d_i\right)=0$

即：

${\lambda }_1=r-\mu ,{\lambda }_2=-d_s,{\lambda }_3=-d_i$

当 $\mu <r$ 时， ${\lambda }_1>0$ ，而 ${\lambda }_2<0$ ， ${\lambda }_3<0$ ，从而 $E_0=\left(0,0,0\right)$ 是不稳定的。

定理4.2若：

$K{k}_1{\eta }_1<d_s$ (5)

成立，则模型(2)的平衡点 $E_1$ 全局稳定。

证明由模型(4)，原模型(2)在平衡点 $E_1\left(K-\frac{K\mu }{r},0,0\right)$ 处的线性化矩阵为：

$J\left(E_1\right)=\left(\begin{array}{ccc}\mu -r& -K{\eta }_1\left(1-\frac{\mu }{r}\right)& -K{\eta }_2\left(1-\frac{\mu }{r}\right)\\ 0& K{k}_1{\eta }_1\left(1-\frac{\mu }{r}\right)-d_s& 0\\ 0& 0& K{k}_2{\eta }_2\left(1-\frac{\mu }{r}\right)-d_i\end{array}\right)$

则 $J\left(E_1\right)$ 的特征方程为：

$\left(\lambda -\mu +r\right)\left[\lambda -K{k}_1{\eta }_1\left(1-\frac{\mu }{r}\right)+d_s\right]\left[\lambda -K{k}_2{\eta }_2\left(1-\frac{\mu }{r}\right)+d_i\right]=0$

即：

${\lambda }_1=\mu -r,{\lambda }_2=K{k}_1{\eta }_1\left(1-\frac{\mu }{r}\right)-d_s,{\lambda }_3=K{k}_2{\eta }_2\left(1-\frac{\mu }{r}\right)-d_i$

当模型(2)满足条件(5)时，由模型假设可知，模型(2)满足：

$K{k}_2{\eta }_2\left(1-\frac{\mu }{r}\right)<K{k}_1{\eta }_1\left(1-\frac{\mu }{r}\right)<K{k}_1{\eta }_1<d_s<d_i$

从而特征根均具有负实部，则平衡点 $E_1$ 局部稳定。

由模型(2)的第一个方程可得 $\underset{t\to +\infty }{\lim }\sup x\left(t\right)\le K$ ，从而对于充分小的 $\epsilon$ ，存在 $T_{\epsilon }>0$ 使得当 $t>T_{\epsilon }$ 时， $x\left(t\right)<K+\epsilon$ 成立，将此不等式替换到模型(2)的第二个方程中，则当 $t>T_{\epsilon }$ 时：

$\begin{array}{c}{P^{\prime }}_s\left(t\right)<k_1{\eta }_1\left(K+\epsilon \right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_s{P}_s\left(t\right)\\ <k_1{\eta }_1\left(K+\epsilon \right)P_s\left(t\right)-d_s{P}_s\left(t\right)\end{array}$ (6)

将式(6)两端同时积分，则：

$P_s\left(t\right)<P_s\left(0\right)\exp \left[{\displaystyle {\int }_0^{\tau }\left(k_1{\eta }_1\left(K+\epsilon \right)-d_s\right)\text{d}s}\right]$

当满足条件(5)时， $k_1{\eta }_1\left(K+\epsilon \right)<d_s$ 对充分小的 $\epsilon$ 成立。因此，当 $t\to +\infty$ 时，可得：

$\underset{t\to \infty }{\lim }{P}_s\left(t\right)=0$ (7)

即存在正常数 $T_{1\epsilon }\ge T_{\epsilon }$ ，使得当 $t\ge T_{1\epsilon }$ 时， $P_s\left(t\right)<\epsilon$ 成立。由模型(2)的第三个方程可得：

${P^{\prime }}_i\left(t\right)<P_i\left(t\right)\left[k_2{\eta }_2\left(K+\epsilon \right)+\beta \epsilon -d_i\right]$ (8)

对式(8)两端同时积分，则：

$P_i\left(t\right)<P_i\left(0\right)\exp \left[{\displaystyle {\int }_0^{\tau }\left(k_2{\eta }_2\left(K+\epsilon \right)+\beta \epsilon -d_i\right)\text{d}s}\right]$

从而，由模型假设及条件(5)，对充分小的 $\epsilon >0$ 时：

$k_2{\eta }_2\left(K+\epsilon \right)+\beta \epsilon <k_1{\eta }_{1}K<d_s<d_i$

成立。从而当 $t\to +\infty$ 时：

$\underset{t\to \infty }{\lim }{P}_i\left(t\right)=0$ (9)

成立。由模型(2)，式(7)和式(9)，可得 $\underset{t\to \infty }{\lim }\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)=\left(K-\frac{K\mu }{r},0,0\right)$ ，从而平衡点 $E_1$ 全局稳定。

定理4.3如果模型(2)满足条件(5)，且满足：

$R_{P_i}:=\frac{K{k}_1{\eta }_1{\eta }_2{d}_s+\beta \left[K{k}_1{\eta }_1\left(r-\mu \right)-r{d}_s\right]}{d_{i}K{k}_1{\eta }_1^2}<1$ (10)

则平衡点 $E_2$ 稳定。其中 $R_{p_i}$ 为患病捕食者 $P_i\left(t\right)$ 的净再生数 [20] 。

证明由模型(4)，模型(2)在平衡点 $E_2=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K},0\right)$ 处的线性化矩阵为：

$J\left(E_2\right)=\left(\begin{array}{ccc}-\frac{r{d}_s}{k_1{\eta }_{1}K}& -\frac{d_s}{k_1}& -\frac{{\eta }_2{d}_s}{k_1{\eta }_1}\\ \frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{{\eta }_{1}K}& 0& 0\\ 0& 0& \frac{k_2{\eta }_2{d}_s}{k_1{\eta }_1}-d_i\end{array}\right)$

则 $J\left(E_2\right)$ 的特征方程为：

$\left[\lambda +d_i-\frac{k_2{\eta }_2{d}_s}{k_1{\eta }_1}\right]\cdot f_1\left(\lambda \right)=0$

其中：

$f_1\left(\lambda \right)={\lambda }^2+\frac{r{d}_s}{k_1{\eta }_{1}K}\lambda -\frac{d_s\left[r{d}_s-k_1{\eta }_{1}K\left(r-\mu \right)\right]}{k_1{\eta }_{1}K}$

假设 $f_1\left(\lambda \right)$ 的两个特征根分别为 ${\lambda }_a,{\lambda }_b$ ，由条件(5)及韦达定理：

${\lambda }_a\cdot {\lambda }_b=-\frac{d_s\left[r{d}_s-k_1{\eta }_{1}K\left(r-\mu \right)\right]}{k_1{\eta }_{1}K}>0$

${\lambda }_a+{\lambda }_b=-\frac{r{d}_s}{k_1{\eta }_{1}K}<0$

成立，从而得到 $f_1\left(\lambda \right)$ 的两个特征根皆有负实部。

再由条件(5)可得：

$\lambda =\frac{k_2{\eta }_2{d}_s}{k_1{\eta }_1}-d_i<0$

故证得平衡点 $E_2=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K},0\right)$ 的局部稳定性。

下证 $E_2$ 的全局稳定性。定义函数 $g\left(w\right)=w-1-\ln w$ ， $w\in R_{+}$ 以及Lyapunov泛函：

$V_1\left(t\right)=k_1{x}_{2}g\left(\frac{x\left(t\right)}{x_2}\right)+P_{2}g\left(\frac{P_s\left(t\right)}{P_2}\right)+P_i\left(t\right)+\beta P_2{\displaystyle {\int }_0^{\tau }f\left(s\right){\displaystyle {\int }_{t-s}^t{P}_i\left(u\right)\text{d}u}}\text{d}s$

计算函数 $V_1\left(t\right)$ 沿着模型(2)的解的全导数，可得：

$\begin{array}{c}{{V^{\prime }}_1\left(t\right)|}_{\left(2\right)}=k_1{x}_2\left[\frac{1}{x_2}-\frac{1}{x\left(t\right)}\right]\cdot x^{\prime }\left(t\right)+P_2\left[\frac{1}{P_2}-\frac{1}{P_s\left(t\right)}\right]\cdot {P^{\prime }}_s\left(t\right)+{P^{\prime }}_i\left(t\right)+\beta P_2{P}_i\left(t\right)\\ -\beta P_2{\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\\ =k_1{x}_2\cdot \frac{x\left(t\right)-x_2}{x_{2}x\left(t\right)}\cdot \left[rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{P}_s\left(t\right)-x\left(t\right){\eta }_2{P}_i\left(t\right)\right]\\ +P_2\left[\frac{P_s\left(t\right)-P_2}{P_2{P}_s(t)}\right]\cdot \left[k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_s{P}_s\left(t\right)\right]\\ +k_2{\eta }_{2}x\left(t\right)P_i(t)+\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_i{P}_i\left(t\right)\\ +\beta P_2{P}_i\left(t\right)-\beta P_2{\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\end{array}$

其中 $E_2\triangleq \left(x_2,P_2,0\right)$ 为模型(2)的平衡点，故有：

$r-\mu ={\eta }_1{P}_2+\frac{r}{K}{x}_2,d_s=k_1{\eta }_1{x}_2$ (11)

因此由式(11)，可得：

$\begin{array}{c}{{V^{\prime }}_1\left(t\right)|}_{\left(2\right)}=k_1\cdot \frac{x\left(t\right)-x_2}{x\left(t\right)}\cdot \left[{\eta }_{1}x\left(t\right)\left(P_2-P_s\left(t\right)\right)+\frac{r}{K}x\left(t\right)\left(x_2-x\left(t\right)\right)-x\left(t\right){\eta }_2{P}_i\left(t\right)\right]\\ +\frac{P_s\left(t\right)-P_2}{P_s\left(t\right)}\cdot \left[k_1{\eta }_1{P}_s\left(t\right)\left(x\left(t\right)-x_2\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\right]\\ +k_2{\eta }_{2}x\left(t\right)P_i\left(t\right)+\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_i{P}_i\left(t\right)\\ +\beta P_2{P}_i\left(t\right)-\beta P_2{\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\end{array}$

$\begin{array}{c}=-\frac{k_{1}r}{K}{\left(x\left(t\right)-x_2\right)}^2+k_1{\eta }_1\left[P_2-P_s\left(t\right)\right]\left[x\left(t\right)-x_2\right]-k_1{\eta }_1\left[P_2-P_s\left(t\right)\right]\cdot \left[x\left(t\right)-x_2\right]\\ +k_2{\eta }_{2}x\left(t\right)P_i\left(t\right)-k_1{\eta }_2{P}_i\left(t\right)\left[x\left(t\right)-x_2\right]-\beta \left[P_s\left(t\right)-P_2\right]{\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_i{P}_i\left(t\right)\\ +\beta P_s(t){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}+\beta P_2{P}_i\left(t\right)-\beta P_2{\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\\ =\left(k_2{\eta }_2-k_1{\eta }_2\right)P_i\left(t\right)x\left(t\right)+\left[\beta P_i\left(t\right)P_2+k_1{\eta }_2{P}_i\left(t\right)x_2-d_i{P}_i\left(t\right)\right]-\frac{k_{1}r}{K}{\left(x\left(t\right)-x_2\right)}^2\\ =\left(k_2{\eta }_2-k_1{\eta }_2\right)P_i\left(t\right)x\left(t\right)+\left[\beta P_2+k_1{\eta }_2{x}_2-d_i\right]\cdot P_i\left(t\right)-\frac{k_{1}r}{K}{\left(x\left(t\right)-x_2\right)}^2\end{array}$

由平衡点 $E_2\triangleq \left(x_2,P_2,0\right)=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K},0\right)$ ，再结合条件(10)可得：

$\beta P_2+k_1{\eta }_2{x}_2-d_i=\frac{K{k}_1{\eta }_1{\eta }_2{d}_s+\beta \left[K{k}_1{\eta }_1\left(r-\mu \right)-r{d}_s\right]}{K{k}_1{\eta }_1^2}-d_i<0$

由模型假设中 $k_2\le k_1$ ，从而 ${{V^{\prime }}_1\left(t\right)|}_{\left(2\right)}\le 0$ 。由文献[21，定理5.3.1]，可证当且仅当 $x\left(t\right)=x_2$ ， $P_s\left(t\right)=P_2$ ， $P_i\left(t\right)=0$ ，有 ${{V^{\prime }}_1\left(t\right)|}_{\left(2\right)}\equiv 0$ 。故由Lyapunov-LaSalle不变性原理 [21] ，模型(2)的平衡点 $E_2$ 全局稳定。

定理4.4 若模型(2)满足条件(3)，且：

$R_{P_s}:=\frac{K{k}_1{\eta }_1{\eta }_2{d}_i-\beta \left[K{k}_2{\eta }_2\left(r-\mu \right)-r{d}_i\right]}{K{k}_2{\eta }_2^2\cdot d_s}<1$ (12)

成立，则平衡点 $E_3$ 稳定。其中 $R_{P_s}$ 为易感捕食者 $P_s\left(t\right)$ 的净再生数 [20] 。

证明由模型(4)，模型(2)在平衡点 $E_3=\left(\frac{d_i}{k_2{\eta }_2},0,\frac{k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i}{k_2{\eta }_2^{2}K}\right)$ 处的线性化矩阵为：

$J\left(E_3\right)=\left(\begin{array}{ccc}-\frac{r{d}_i}{k_2{\eta }_{2}K}& -\frac{{\eta }_1{d}_i}{k_2{\eta }_2}& -\frac{d_i}{k_2}\\ 0& \frac{K{k}_1{\eta }_1{\eta }_2{d}_i-\beta \left[k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i\right]}{k_2{\eta }_2^{2}K}-d_s& 0\\ \frac{k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i}{{\eta }_{2}K}& \frac{\beta \left[k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i\right]}{k_2{\eta }_2^{2}K}& 0\end{array}\right)$

则 $J\left(E_3\right)$ 的特征方程为：

$\left[\lambda +d_s-\frac{K{k}_1{\eta }_1{\eta }_2{d}_i-\beta \left[k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i\right]}{k_2{\eta }_2^{2}K}\right]f_2\left(\lambda \right)=0$

其中：

$f_2\left(\lambda \right)={\lambda }^2+\frac{r{d}_i}{k_2{\eta }_{2}K}\lambda -\frac{d_i\left[r{d}_i-k_2{\eta }_{2}K\left(r-\mu \right)\right]}{k_2{\eta }_{2}K}$

假设 $f_2\left(\lambda \right)$ 的两个特征根分别为 ${\lambda }_c,{\lambda }_d$ ，由韦达定理及条件(3)可得：

${\lambda }_c\cdot {\lambda }_d=-\frac{d_i\left[r{d}_i-k_2{\eta }_{2}K\left(r-\mu \right)\right]}{k_2{\eta }_{2}K}>0$ , ${\lambda }_c+{\lambda }_d=-\frac{r{d}_i}{k_2{\eta }_{2}K}<0$

从而 $f_2\left(\lambda \right)$ 的两个特征根皆有负实部。

由条件(12)，可得：

$\lambda =\frac{K{k}_1{\eta }_1{\eta }_2{d}_i-\beta \left[k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i\right]}{k_2{\eta }_2^{2}K}-d_s<0$

即平衡点 $E_3=\left(\frac{d_i}{k_2{\eta }_2},0,\frac{k_2{\eta }_2\left(r-\mu \right)-r{d}_i}{k_2{\eta }_2^{2}K}\right)$ 的局部稳定性成立。

下面证明 $E_3$ 的全局渐近稳定性。定义函数 $g\left(w\right)=w-1-\ln w$ ， $w\in R_{+}$ 以及Lyapunov泛函：

$V_2\left(t\right)=k_2{x}_{3}g\left(\frac{x\left(t\right)}{x_3}\right)+P_{3}g\left(\frac{P_i\left(t\right)}{P_3}\right)+P_s(\; t\; )$

计算 $V_2\left(t\right)$ 沿着模型(2)的解的全导数，可得：

$\begin{array}{c}{{V^{\prime }}_2\left(t\right)|}_{\left(2\right)}=k_2{x}_3\left[\frac{1}{x_3}-\frac{1}{x\left(t\right)}\right]\cdot x^{\prime }\left(t\right)+P_3\left[\frac{1}{P_3}-\frac{1}{P_i\left(t\right)}\right]\cdot {P^{\prime }}_i\left(t\right)\\ +\left[k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_s{P}_s\left(t\right)\right]\\ =k_2\left[x\left(t\right)-x_3\right]\cdot \frac{1}{x\left(t\right)}\cdot \left[rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{P}_s\left(t\right)-x\left(t\right){\eta }_2{P}_i\left(t\right)\right]\\ +\left[P_i\left(t\right)-P_3\right]\cdot \frac{1}{P_i\left(t\right)}\cdot \left[k_2{\eta }_{2}x\left(t\right)P_i\left(t\right)+\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_i{P}_i\left(t\right)\right]\\ +k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-d_s{P}_s(\; t\; )\end{array}$

由于 $E_3\triangleq \left(x_3,0,P_3\right)$ 为模型(2)的平衡点，可得：

$r-\mu ={\eta }_2{P}_3+\frac{r}{K}{x}_3,d_i=k_2{\eta }_2{x}_3$ (13)

因此由式(13)，可得：

$\begin{array}{c}{{V^{\prime }}_2\left(t\right)|}_{\left(2\right)}=k_2\left[x\left(t\right)-x_3\right]\cdot \left[{\eta }_2\left(P_3-P_i\left(t\right)\right)+\frac{r}{K}\left(x_3-x\left(t\right)\right)-{\eta }_1{P}_s\left(t\right)\right]\\ +\left[P_i\left(t\right)-P_3\right]\cdot \left[k_2{\eta }_2\left(x\left(t\right)-x_3\right)\right]-\beta P_3{P}_s\left(t\right)-d_s{P}_s\left(t\right)\\ +\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}+k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\end{array}$

$\begin{array}{c}=-\frac{k_{2}r}{K}{\left(x\left(t\right)-x_3\right)}^2+k_2{\eta }_2\left[P_3-P_i\left(t\right)\right]\left[x\left(t\right)-x_3\right]-k_2{\eta }_2\left[P_3-P_i\left(t\right)\right]\cdot \left[x\left(t\right)-x_3\right]\\ -k_2{\eta }_1{P}_s\left(t\right)\left[x\left(t\right)-x_3\right]+\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}-\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}\\ +k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-P_3\beta P_s\left(t\right)-d_s{P}_s\left(t\right)\\ =\left(k_1{\eta }_1-k_2{\eta }_1\right)P_s\left(t\right)x\left(t\right)+\left[k_2{\eta }_1{x}_3-P_3\beta -d_s\right]\cdot P_s\left(t\right)-\frac{k_{2}r}{K}{\left(x\left(t\right)-x_3\right)}^2\end{array}$

由于 $E_3\triangleq \left(x_3,0,P_3\right)=\left(\frac{d_i}{k_2{\eta }_2},0,\frac{k_2{\eta }_{2}K\left(r-\mu \right)-r{d}_i}{k_2{\eta }_2^{2}K}\right)$ ，从而：

$\begin{array}{l}{{V^{\prime }}_2\left(t\right)|}_{\left(2\right)}=-\frac{k_{2}r}{K}{\left(x\left(t\right)-x_3\right)}^2+\left(k_1-k_2\right){\eta }_{1}x\left(t\right)P_s\left(t\right)\\ +\left[\frac{K{k}_2{\eta }_1{\eta }_2{d}_i-\beta \left[K{k}_2{\eta }_2\left(r-\mu \right)-r{d}_i\right]}{K{k}_2{\eta }_2^2}-d_s\right]\cdot P_s(\; t\; )\end{array}$

当 $k_1=k_2$ ，且条件(12)成立时可得 ${{V^{\prime }}_2\left(t\right)|}_{\left(2\right)}\le 0$ 。由文献[21，定理5.3.1]，可证当且仅当 $x\left(t\right)=x_3$ ， $P_s\left(t\right)=0$ ， $P_i\left(t\right)=P_3$ 时， ${{V^{\prime }}_2\left(t\right)|}_{\left(2\right)}\equiv 0$ 。故由Lyapunov-LaSalle不变性原理 [21] ，模型(2)的平衡点 $E_3$ 全局稳定。

5. 患病捕食者的一致持久性

定理5.1若模型(2)满足条件(3)、(5)、(10)，则 $P_i\left(t\right)$ 一致持久，即下列不等式对常数 $\delta >0$ 成立：

$\underset{t\to \infty }{\lim }\inf P_i\left(t\right)>\delta$

证明令 $C\left(\left[0,+\infty \right),{ℝ}_{\text{+}}^3\right)$ 为从 $\left[0,+\infty \right)$ 到 ${ℝ}_{\text{+}}^3$ 的连续函数映射空间 [22] 。定义：

$X:=C\left(\left[0,+\infty \right),{ℝ}_{\text{+}}^3\right)$

$X^0:=\left\{\phi \in X:{\phi }_3\left(0\right)>0\right\}$

$\partial X^0=X\backslash X^0$

这里T为基于X的连续半流，且 $T\left(t\right)$ 为基于X的 $C^0$ -半群对任意的 $t\ge 0$ 成立，这里：

$T\left(t\right):X^0\to X^0,T\left(t\right):\partial X^0\to \partial X^0$

由 $X^0$ 和 $\partial X^0$ 的定义以及命题3.1，可得存在常数 $t_0\ge 0$ 使得 $T\left(t\right)$ 对于 $t\ge t_0$ 是紧的，且 $T\left(t\right)$ 在X中最终一致有界。令 $\omega \left(\phi \right)$ 为轨道：

${\gamma }^{+}\left(\phi \right)=\left\{T\left(t\right)\phi :\forall t\ge 0\right\}$

的 $\omega$ 极限集，定义 ${\tilde{X}}_{\partial }$ 是特殊不变集，此不变集为：

${\tilde{X}}_{\partial }=\left\{\phi \in \partial X^0:T\left(t\right)\phi \in \partial X^0\right\}$

下面考虑 $\partial X^0$ 的动力学性态，当 $t\ge 0$ ， $P_i\equiv 0$ 时，模型(2)可以退化为如下模型：

$\begin{array}{l}{x}^{\prime }\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{\mu }\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{P}_s\left(t\right)\\ {P^{\prime }}_s\left(t\right)=k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-d_s{P}_s\left(t\right)\end{array}$ (14)

则模型(14)有如下三个平衡点：

${\hat{E}}_0\left(0,0\right),{\hat{E}}_1\left(K-\frac{K\mu }{r},0\right),{\hat{E}}_2=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K}\right)$

其中平衡点 ${\hat{E}}_0$ 是不稳定的；根据条件(5)可知，平衡点 ${\hat{E}}_1$ 稳定；根据条件(3)和条件(10)可知，平衡点 ${\hat{E}}_2$ 稳定，故 ${\tilde{X}}_{\partial }$ 是非循环的。由模型(2)可得：对任意的 $\phi$ 属于 ${\tilde{X}}_{\partial }$ ，有 $\omega \left(\phi \right)=\left\{E_0,E_1,E_2\right\}$ ，则 ${\tilde{X}}_{\partial }$ 中的流满足孤立非循环。

下面证明 $E_0$ ， $E_1$ 和 $E_2$ 对于 $X^0$ 是一致弱排斥的。

步骤1 首先证明 $W^s\left(E_0\right)\cap X^0=\varnothing$ 。如若不然，则 $W^s\left(E_0\right)\cap X^0\ne \varnothing$ ，从而存在模型(2)的解 $\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)$ 满足 $\underset{t\to \infty }{\lim }\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)=\left(0,0,0\right)$ 。则对任意小的正常数 $\eta$ 满足 $\eta <K$ ，存在正常数 $T_1=T_1\left(\eta \right)$ 使得当 $t\ge T_1$ 时：

$x\left(t\right)<\eta ,P_s\left(t\right)<\eta ,P_i\left(t\right)<\eta$

成立。由模型(2)的第一个方程：

$x^{\prime }\left(t\right)>rx\left(1-\frac{x}{K}\right)-\mu x-x{\eta }_1\eta -x{\eta }_2\eta$

成立。从而，由 $\eta$ 的任意性和比较原理：

$\underset{t\to \infty }{\lim }\inf x\left(t\right)\ge K$

成立。这与 $t\ge T_1$ 时， $x\left(t\right)<\eta <K$ 矛盾。即 $W^s\left(E_0\right)\cap X^0=\varnothing$ 。

步骤2接着证明 $W^s\left(E_1\right)\cap X^0=\varnothing$ 。如若不然，则 $W^s\left(E_1\right)\cap X^0\ne \varnothing$ ，即存在模型(2)的解 $\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)$ 使得：

$\underset{t\to \infty }{\lim }\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)=\left(K-\frac{K\mu }{r},\text{0,}\text{0}\right)$

对于与步骤1中相同的 $\eta$ ，存在正常数 $T_2=T_2\left(\eta \right)\ge T_1$ ，使得当 $t\ge T_2$ 时，可得：

$x\left(t\right)>K-\frac{K\mu }{r}-\eta ,P_s\left(t\right)<\eta ,P_i\left(t\right)<\eta$

由模型(2)的第三个方程，当 $t\ge T_2$ 时，可得：

${P^{\prime }}_i\left(t\right)>k_2{\eta }_2\left(K-\frac{K\mu }{r}-\eta \right)P_i\left(t\right)-d_i{P}_i(\; t\; )$

考虑辅助方程：

${{\psi }^{\prime }}_i\left(t\right)>k_2{\eta }_2\left(K-\frac{K\mu }{r}-\eta \right){\psi }_i\left(t\right)-d_i{\psi }_i\left(t\right),t\ge T_2$ (15)

由式(15)及比较原理，当 $t\ge T_2$ 时， $P_i\left(t\right)>{\psi }_i\left(t\right)$ 。由条件(3)，即 $K{k}_2{\eta }_2<d_i$ 时 $\underset{t\to \infty }{\lim }\sup P_i\left(t\right)>\eta$ 成立，这与 $t\ge T_2$ 时， $P_i\left(t\right)<\eta$ 矛盾。即 $W^s\left(E_1\right)\cap X^0=\varnothing$ 。

步骤3最后证明 $W^s\left(E_2\right)\cap X^0=\varnothing$ 。如若不然，则 $W^s\left(E_2\right)\cap X^0\ne \varnothing$ ，即存在模型(2)的解 $\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)$ 使得：

$\underset{t\to \infty }{\lim }\left(x\left(t\right),P_s\left(t\right),P_i\left(t\right)\right)=\left(\frac{d_s}{k_1{\eta }_1},\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K},\text{0}\right)$

对于与步骤2中相同的 $\eta$ ，存在正常数 $T_3=T_3\left(\eta \right)\ge T_1$ ，使得当 $t\ge T_3$ 时：

$x\left(t\right)>\frac{d_s}{k_1{\eta }_1}-\eta ,P_s\left(t\right)>\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K}-\eta ,P_i\left(t\right)<\eta$

由模型(2)的第三个方程，当 $t\ge T_3$ 时，有：

$P_i\left(t\right)>k_2{\eta }_2\left(\frac{d_s}{k_1{\eta }_1}-\eta \right)P_i\left(t\right)+\beta \left(\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K}-\eta \right)P_i\left(t\right)-d_i{P}_i(\; t\; )$

考虑辅助方程如下：

${\widetilde{{\psi }^{\prime }}}_i\left(t\right)=k_2{\eta }_2\left(\frac{d_s}{k_1{\eta }_1}-\eta \right){\tilde{\psi }}_i\left(t\right)+\beta \left(\frac{k_1{\eta }_{1}K\left(r-\mu \right)-r{d}_s}{k_1{\eta }_1^{2}K}-\eta \right){\tilde{\psi }}_i\left(t\right)-d_i{\tilde{\psi }}_i\left(t\right),t\ge T_3$ (16)

由式(16)及比较原理，当 $t\ge T_3$ 时， $P_i\left(t\right)>{\tilde{\psi }}_i\left(t\right)$ 。由条件(3)，即 $K{k}_2{\eta }_2<d_i$ 时，可得 $\underset{t\to \infty }{\lim }\sup P_i\left(t\right)>\eta$ ，这与 $t\ge T_3$ 时 $P_i\left(t\right)<\eta$ 矛盾。从而 $W^s\left(E_2\right)\cap X^0=\varnothing$ 。

上述结果意味着在最大值范数意义下，不等式：

$\underset{t\to \infty }{\lim }\sup \Vert T\left(t\right)\phi -E_i\Vert \ge \eta ,\forall \phi \in X^0,i=0,1,2$

成立，故 $E_0,E_1,E_2$ 对 $X^0$ 一致弱排斥。

从而存在正常数 $\delta >0$ 使得对于模型(2)的解 [22] ：

$\underset{t\to \infty }{\lim }\inf P_i\left(t\right)>\delta$

成立，即患病捕食者一致持久生存。

6. 数值模拟

数值模拟图将直观的展示本文模型中食饵和捕食者种群数量随时间变化的规律，本文数值模拟的数据主要参考文献 [16] 。

令模型(2)中的 $f\left(s\right)=\delta \left(s-\tau \right)$ ，这里的 $\delta$ 为狄拉克函数，则模型(2)可简化为如下模型：

$\{\begin{array}{l}{x}^{\prime }\left(t\right)=rx\left(t\right)\left(1-\frac{x\left(t\right)}{K}\right)-\mu x\left(t\right)-x\left(t\right){\eta }_1{P}_s\left(t\right)-x\left(t\right){\eta }_2{P}_i\left(t\right)\hfill \\ {P^{\prime }}_s\left(t\right)=k_1{\eta }_{1}x\left(t\right)P_s\left(t\right)-\beta P_s\left(t\right)P_i\left(t-\tau \right)-d_s{P}_s\left(t\right)\hfill \\ {P^{\prime }}_i\left(t\right)=k_2{\eta }_{2}x\left(t\right)P_i\left(t\right)+\beta P_s\left(t\right)P_i\left(t-\tau \right)-d_i{P}_i\left(t\right)\hfill \end{array}$ (17)

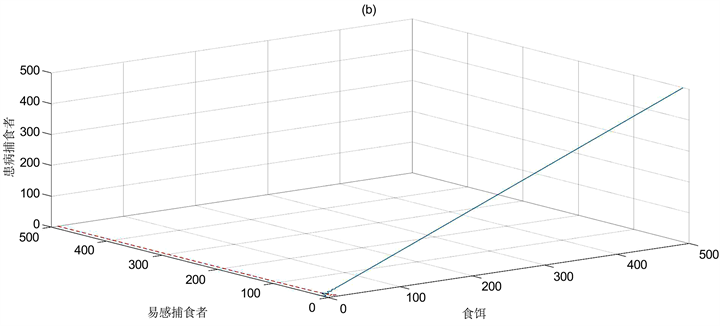
Figure 1. Global asymptotic stability of $E_2$ when $\begin{array}{c}{R}_{P_i}<1\end{array}$

图1. 当 $\begin{array}{c}{R}_{P_i}<1\end{array}$ 时 $E_2$ 的全局渐近稳定性

图1(a)，图1(b)分别展示了模型(17)中边界平衡点 $E_2$ 的稳定性，当患病捕食者 $P_i\left(t\right)$ 的净再生数 $R_{P_i}<1$ 时，易感捕食者与食饵共存。参数选取如下：

$\begin{array}{l}r=2,\beta =0.01,K=100,d_s=0.9,\tau =5,d_i=0.2,\\ k_1=0.4,k_2=0.1,\mu =0.05\text{,}{\eta }_1=0.2\text{,}{\eta }_2=0.06\text{.}\end{array}$

初值为： $\left(18,10,5\right)$

数值模拟图1(a)、图1(b)验证了文中定理4.3的正确性，即当条件(10)成立时边界平衡点 $E_2$ 是全局渐近稳定的。图2展示了当模型(17)满足条件(3)、条件(5)以及条件(10)时，患病捕食者 $P_i\left(t\right)$ 一致持久生存(见定理5.1)。

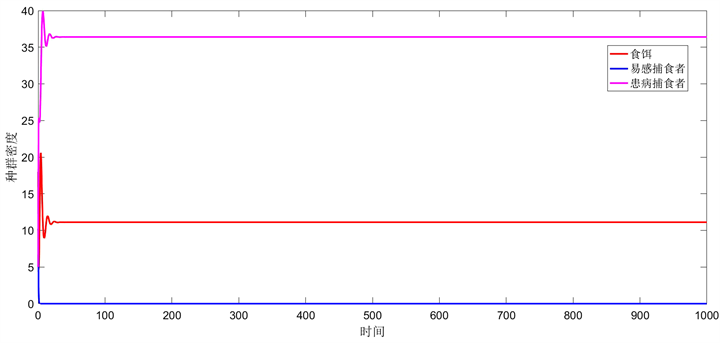
Figure 2. Infected predator $P_i\left(t\right)$ uniform persistence

图2. 患病捕食者 $P_i\left(t\right)$ 一致持久生存

图2展示了模型(17)，当 $R_{P_i}>1$ 且 $R_{P_s}<1$ 时，患病捕食者 $P_i\left(t\right)$ 一致持久生存，参数选取如下：

$\begin{array}{l}r=3,\beta =0.9,K=80,d_s=0.04,\tau =3,d_i=0.2,\\ k_1=0.6,k_2=0.3,\mu =0.4,{\eta }_1=0.5,{\eta }_2=0.06.\end{array}$

初值为： $\left(18,10,5\right)$

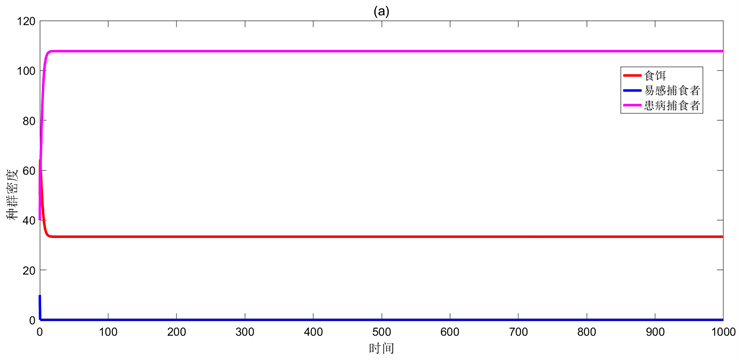
Figure 3. Global asymptotic stability of $E_3$ when $\begin{array}{c}{R}_{P_s}<1\end{array}$

图3. 当 $\begin{array}{c}{R}_{P_s}<1\end{array}$ 时 $E_3$ 的全局渐近稳定性

图3(a)，图3(b)分别展示了模型(17)中边界平衡点 $E_3$ 的稳定性，当易感捕食者 $P_s\left(t\right)$ 的净再生数 $R_{P_s}<1$ 时，患病捕食者与食饵共存，参数选取如下：

$\begin{array}{l}r=10,\beta =0.9,K=100,d_s=0.1,\tau =5,d_i=0.2,\\ k_1=0.7,k_2=0.1,\mu =0.2,{\eta }_1=0.2,{\eta }_2=0.06.\end{array}$

初值为： $\left(18,10,5\right)$

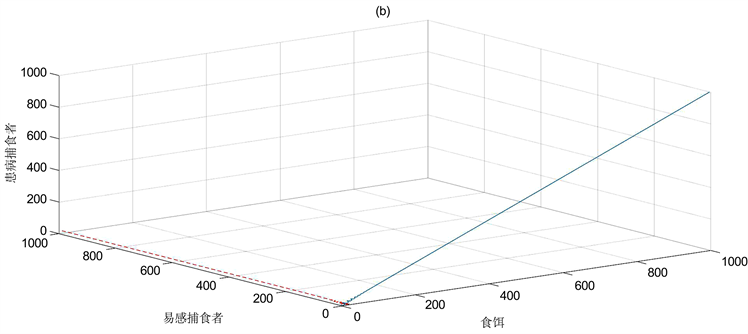
Figure 4. Global asymptotic stability of $E_4$

图4. $E_4$ 的全局渐近稳定性

图4展示了模型(17)中食饵和捕食者共存状态下的平衡点 $E_4$ 的稳定性，参数选取如下：

$\begin{array}{l}r=3,\beta =0.02,K=80,d_s=0.1,\tau =5,d_i=0.2,\\ k_1=0.4,k_2=0.1,\mu =0.2,{\eta }_1=0.2,{\eta }_2=0.06.\end{array}$

初值为： $\left(18,10,5\right)$

为了对比模型(1)与模型(2)在分别采取不同疾病发生率 $\beta$ 的情形下系统解的动力学性态，本文针对以下一组数据进行了数值模拟，见图5(a)，图5(b)，图5(c)和图6(a)，图6(b)，图6(c)：

$\begin{array}{l}r=3,K=80,d_s=0.1,\tau =5,d_i=0.2,\\ k_1=0.4,k_2=0.1,\mu =0.2,{\eta }_1=0.2,{\eta }_2=0.06.\end{array}$

初值为： $\left(18,10,5\right)$

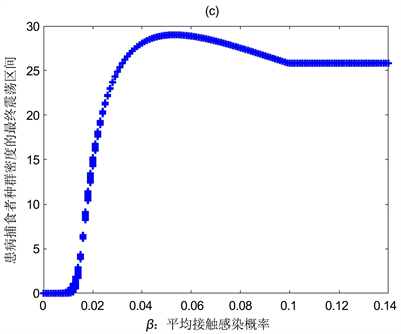
Figure 5. The relationship between the population's own density in model (17) and the Average contact infection rate $\beta$

图5. 模型(17)中种群自身密度与平均接触感染率 $\beta$ 之间的关系

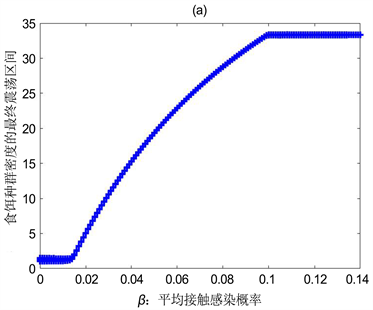
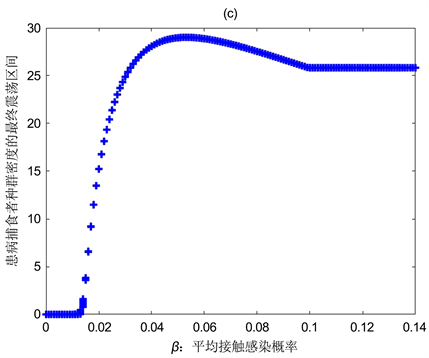
Figure 6. The relationship between the population’s own density in model (1) and the Average contact infection rate $\beta$

图6. 模型(1)中种群自身密度与平均接触感染率 $\beta$ 之间的关系

图5(a)，图5(b)，图5(c)展示了在模型(17)中，平均接触感染率 $\beta$ 对模型(17)中种群数量的稳定性的影响。从图5(a)中可以发现，大约当 $\beta \in \left(0.02,0.1\right)$ 时，食饵密度的垂直振幅变得越来越大，当 $\beta \ge 0.1$ 时食饵种群的数量变得稳定；从图5(b)中可以发现，大约当 $\beta \in \left(0.02,0.1\right)$ 时，易感捕食者的种群密度的振幅减小，直到 $\beta \ge 0.1$ 以后易感捕食者的种群数量开始变的稳定。

图6(a)，图6(b)，图6(c)展示了在模型(1)中，平均接触感染率 $\beta$ 对模型(1)的解的渐近稳定性的影响。从图6(c)中可以发现，大约当 $\beta \in \left(0.02,0.1\right)$ 时，患病捕食者密度的垂直振幅经历了由大变小最后稳定的情形，在 $\beta \ge 0.1$ 以后患病捕食者的种群数量开始变的稳定。

与模型(1)相比，模型(2)将模型(1)的双线性疾病发生率 $\beta P_s\left(t\right)P_i\left(t\right)$ 变为具有分布时滞的疾病发生率 $\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}$ ，在图5与图6中，图形的变化并未出现明显区别，可见平均接触感染率 $\beta$ 并非主要影响解的性态的因素。

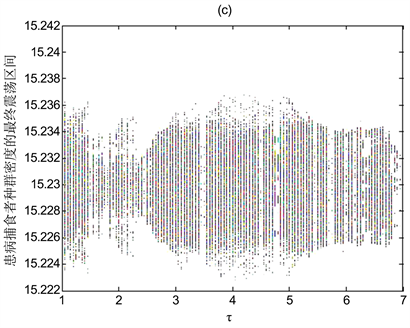
Figure 7. The relationship between the population’s own density in model (17) and the maximum incubation period after infection of a population with a disease $\tau$

图7. 模型(17)中种群自身密度与种群感染疾病后的最大潜伏期 $\tau$ 之间的关系

图7(a)，图7(b)，图7(c)分别展示了模型(17)中，种群自身密度与种群感染疾病后的最大潜伏期 $\tau$ 之间的关系，参数选取如下：

$\begin{array}{l}r=3,\beta =0.02,K=80,d_s=0.1,d_i=0.2,\\ k_1=0.4,k_2=0.1,\mu =0.2,{\eta }_1=0.2,{\eta }_2=0.06.\end{array}$

初值为： $\left(18,10,5\right)$

图7(a)，图7(b)，图7(c)展示了在模型(17)中，种群感染疾病后的最大潜伏期 $\tau$ 对模型(17)中种群数量的稳定性的影响。图7的横轴用来表示疾病潜伏期的时间尺度，在数值模拟时选择疾病的最长潜伏期为7 (可视为7天、7个月或者7年)，图7(a)，图7(b)，图7(c)展示了疾病潜伏期的长短影响着模型解的稳定性。当疾病潜伏期 $\tau$ 的取值约在1.5~2.5之间时，食饵和捕食者种群的震荡区间相对较小；对比图7(a)，图7(b)，图7(c)，从横轴选定的整个时间尺度上观察，相较于对食饵和易感捕食者种群稳定性的影响而言，较长的疾病潜伏期对患病捕食者的种群稳定性更有利，此外图7也展示了模型(17)的解对疾病潜伏期 $\tau$ 的敏感性。

7. 结论

本文提出了一个捕食者患病且具有分布时滞感染率的捕食–食饵模型。文中假设易感捕食者和患病捕食者同时捕获食饵，捕食者种群中疾病感染率的形式为分布时滞的形式，为了提出本文研究的生态传染病模型，文中提出了一些符合生物意义的合理假设。正文中，运用单调动力系统理论获得了捕食者灭绝平衡点 $E_1$ 的稳定性，并通过构造Lyapunov泛函的方法分别获得了患病捕食者灭绝平衡点 $E_2$ 和易感捕食者灭绝平衡点 $E_3$ 的稳定性。文中定义了捕食者的净再生数，得出当患病捕食者净再生数 $R_{P_i}<1$ 时 $E_2$ 稳定；当易感捕食者净再生数 $R_{P_s}<1$ 时 $E_3$ 稳定的结论。此外患病捕食者一致持久生存的充分条件通过一致持久生存理论得以证明。

其次，数值模拟图直观的展示了模型(1)的理论结果的正确性：图1~3不仅展示了 $E_2$ 和 $E_3$ 的全局渐近稳定性，也展示了当患病捕食者 $P_i\left(t\right)$ 和易感捕食者 $P_s\left(t\right)$ 的净再生数分别小于1时， $E_2$ 和 $E_3$ 的全局稳定性。图4展示了食饵和捕食者共存平衡点 $E_4$ 的全局渐近稳定性。本文将模型(1)与模型(2)中具有双线性疾病发生率与具有分布时滞疾病发生率的情形下，就平均接触感染概率 $\beta$ 的不同取值对模型的渐近稳定性的影响进行了分析(见图5和图6)。分析可得，若将模型(1)中的双线性疾病发生率 $\beta P_s\left(t\right)P_i\left(t\right)$ 变化为模型(2)中具有分布时滞的疾病发生率 $\beta P_s\left(t\right){\displaystyle {\int }_0^{\tau }f\left(s\right)P_i\left(t-s\right)\text{d}s}$ ，图5和图6展示了种群的动力学性态并未出现明显的变化，这表明平均接触感染率 $\beta$ 并非影响解的性态的主要参数。图7(a)，图7(b)，图7(c)展示了疾病潜伏期 $\tau$ 对模型(17)中解的稳定性的影响。图7首先展示了疾病潜伏期的长短影响着模型解的稳定性，其次展示了当疾病潜伏期 $\tau$ 的取值约在1.5~2.5之间时，食饵和捕食者种群的震荡区间相对较小的性态。再次，图7(a)，图7(b)，图7(c)也展示了相较于对食饵和易感捕食者种群稳定性的影响而言，较长的疾病潜伏期对患病捕食者的种群稳定性更有利，因此模型(17)解的稳定性对疾病潜伏期 $\tau$ 的敏感性更强，也表明了疾病潜伏期 $\tau$ 是影响模型解的稳定性的重要参数。

本文中的模型并未考虑食饵和捕食者的年龄结构、对共存平衡点的稳定性也并未进行理论的证明，这些工作有待以后去解决。

致谢

在此特别感谢东北石油大学专项–省高校基本科研业务费项目(项目代码：2022TSTD-05)以及东北石油大学–人才引进科研启动经费资助项目的支持(项目代码：1305021838)。

NOTES

^*通讯作者。