具有隐藏状态的随机营养物质–浮游植物模型的长期行为

Long-Term Behavior of a Randomnutrient- Phytoplankton Model with Hidden State

摘要: 本文主要研究具有隐藏状态的营养物质–浮游植物模型的长期行为。首先，构造适当的李雅普诺夫函数，利用强马尔可夫性质，证明具有隐藏状态的随机营养物质–浮游植物模型解的存在唯一性和费勒过程；其次，讨论由非线性滤波器的遍历性和李雅普诺夫函数构造的阈值λ；最后，再运用弱收敛性和强大数定律等相关知识，证明了具有隐藏状态的随机营养物质–浮游植物模型解的灭绝性和持久性。

Abstract: This article mainly studies the long-term behavior of a nutrient-floating plant model with a hidden state. Firstly, the properly constructed Lee Yapanov function, using strong Marcov’s nature to prove that the existence of random nutrients with a hidden state-floating plant model solution is unique and Ferler’s process; secondly, discuss the ergodicity of nonlinear filters and the threshold con-structed by Lyapunov functions; finally, by applying relevant knowledge such as weak convergence and strong laws of large numbers, the extinction and persistence of solutions for the stochastic nu-trient phytoplankton model with hidden states were proved.

1. 引言

在生态系统中，浮游生物两者需要依靠营养物质维持生存并受其影响。营养物质作为生物生存的必要条件，但随着经济的发展，流入水中的营养物质对环境的危害较大，以及造成微藻生物柴油减少。中国作为海洋面积世界第三大以及拥有不少湖泊的国家，研究浮游生物是生态系统中重要的问题之一，对保护环境和人类的发展具有极大的价值作用。在这样的背景下，与此相关问题吸引了不少研究者，研究者开始考虑到浮游动植物在相互作用 [1] [2] [3] 的过程中，浮游植物自身也需要摄入营养物质。如Ruan [4] [5] 在浮游生物相互作用模型中指出了营养物质对浮游生物种群增长的重要性。因此，为更好的了解浮游生物，合理解决有害的浮游生物，不少研究者对营养物质与浮游动植物相互作用模型进行研究。此模型系统可以由以下微分方程描述：

$\{\begin{array}{l}\text{d}N\left(t\right)=\left[D\left(N^0-N\left(t\right)\right)-\frac{{\alpha }_{1}P\left(t\right)N\left(t\right)}{K_1+N\left(t\right)}\right]\text{d}t,\hfill \\ \text{d}P\left(t\right)=\left[\frac{{\alpha }_{2}P\left(t\right)N\left(t\right)}{K_1+N\left(t\right)}-C\left(P\left(t\right)\right)Z\left(t\right)-D_{1}P\left(t\right)\right]\text{d}t,\hfill \\ \text{d}Z\left(t\right)=\left[{\beta }_{1}C\left(P\left(t\right)\right)Z\left(t\right)-D_{2}P\left(t\right)\right]\text{d}t.\hfill \end{array}$ (1)

其中

$C\left(P\left(t\right)\right)=\frac{e_1{\sigma }_{1}P\left(t\right)}{1+h{e}_1{\sigma }_{1}P\left(t\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(t\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(t\right)\right)}\right).$

系统(1)的初始条件为

$N\left(0\right)>0,P\left(0\right)>0,Z\left(0\right)>0.$

其中 $N\left(t\right),P\left(t\right),Z\left(t\right)$ 分别表示t时刻营养物质的浓度、浮游植物种群的浓度、浮游动物种群的浓度。 $N^0$ 表示营养物质的恒定输入量，D表示营养物质的稀释率， ${\alpha }_1$ 表示浮游植物种群的养分稀释率， ${\alpha }_2$ 表示浮游植物种群生长的养分转化率， $e_1$ 表示每单位浮游植物种类的相遇率， ${\sigma }_1$ 表示浮游动物摄食所遇到的食物生物量的比例( $0<{\sigma }_1\le 1$ )。h表示单位生物量的处理时间，其中包含了消化道处理该物质所需的时间。 $1-\frac{f\left(N\right)}{4G_1}$ 表示毒素决定的功能反应,说明了毒素的负效应，其中 $G_1=\frac{M_1}{T_1}$ ， $M_1$ 表示衡量单位时间内浮游动物能耐受最大毒素量的度量， $T_1$ 表示当浮游动物耐受的毒素浓度降低(高毒性)或毒素浓度在浮游植物生物量增加时， $G_1$ 下降。 $D_1$ 表示浮游植物种群的死亡率， $D_2$ 表示浮游动物种群的死亡率， ${\beta }_1$ 表示浮游动物的最大转化率， $K_1$ 表示考虑相应霍林——II型函数来描述以 $K_1$ 为半饱和函数的放牧现象。因子4只是一个数，它将 $C\left(P\right)$ 的峰值形式简化为P。

在上述式(1)中，选择二维的营养物质–浮游植物模型进行研究。为了使该模型更为逼真，必须考虑温度、气候、水资源等各种因素对模型的影响，得到的随机营养物质–浮游植物模型如下：

$\{\begin{array}{c}\text{d}N\left(t\right)=\left[D{N}^0-DN\left(t\right)-P\left(t\right)y\left(N\left(t\right),P\left(t\right)\right)\right]\text{d}t+{\varrho }_{1}N\left(t\right)\text{d}{B}_1\left(t\right),\\ \begin{array}{l}\text{d}P\left(t\right)=\left[-D_{1}P\left(t\right)-\frac{e_1{\sigma }_{1}P\left(t\right)}{1+h{e}_1{\sigma }_{1}P\left(t\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(t\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(t\right)\right)}\right)\left(\gamma -P\left(t\right)\right)+P\left(t\right)y\left(N\left(t\right),P\left(t\right)\right)\right]\text{d}t\\ +{\varrho }_{2}P\left(t\right)\text{d}{B}_2\left(t\right),\end{array}\end{array}$ (2)

其中 $B_1\left(t\right),B_2\left(t\right)$ 为独立的布朗运动和 ${\varrho }_1,{\varrho }_2\ne 0$ 为噪声强度。假设 $P\left(t\right)+Z\left(t\right)=\gamma$ , $\gamma$ 为正常数，相比较与模型(1)，重新定义以上的系数：

$\frac{{\alpha }_{1}P\left(t\right)N\left(t\right)}{K_1+N\left(t\right)}=\frac{{\alpha }_{2}P\left(t\right)N\left(t\right)}{K_1+N\left(t\right)}=P\left(t\right)y\left(N\left(t\right),P\left(t\right)\right).$

在生态学中，浮游植物依靠无机营养物质存活，如氮、磷、碳水化合物等。但有些浮游植物依赖于隐藏状态的营养物质，不能直接观察到，因此，在模型中加入隐藏状态的营养物质。为实现目标，需对营养物质进行分类，在分类设置中一类考虑的是未隐藏的营养物质，即仍用 $P\left(t\right)y\left(N\left(t\right),P\left(t\right)\right)$ 表示。另一类包含隐藏的营养物质，即 $P\left(t\right)g\left(N\left(t\right),P\left(t\right)\right)$ 。设 $\alpha \left(t\right)$ 为取值在 $\mathcal{M}=\left[0,1\right]$ 中的马尔可夫过程。假设 $\alpha \left(t\right)$ 表示隐藏状态类中的营养物质在 $t\ge 0$ 时刻被转化的营养物质百分比，并且只有 $\alpha \left(t\right)$ 在噪声损坏下的观测是可用的。因此，让函数y和g依赖于 $\alpha \left(t\right)$ ，利用式(2)的隐态动力学，得出具有隐藏状态的随机营养物质–浮游植物模型：

$\{\begin{array}{l}\text{d}N\left(t\right)=\left[D{N}^0-DN\left(t\right)-P\left(t\right)y\left(\alpha \left(t\right),N\left(t\right),P\left(t\right)\right)-\alpha \left(t\right)P\left(t\right)g\left(\alpha \left(t\right),N\left(t\right),P\left(t\right)\right)\right]\text{d}t+{\varrho }_{1}N\left(t\right)\text{d}{B}_1\left(t\right),\hfill \\ \begin{array}{l}\text{d}P\left(t\right)=[-D_{1}P\left(t\right)-\frac{e_1{\sigma }_{1}P\left(t\right)}{1+h{e}_1{\sigma }_{1}P\left(t\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(t\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(t\right)\right)}\right)\left(\gamma -P\left(t\right)\right)+P\left(t\right)y\left(\alpha \left(t\right),N\left(t\right),P\left(t\right)\right)\\ \begin{array}{c}\\ \end{array}+\alpha \left(t\right)P\left(t\right)g\left(\alpha \left(t\right),N\left(t\right),P\left(t\right)\right)]\text{d}t+{\varrho }_{2}P\left(t\right)\text{d}{B}_2\left(t\right).\end{array}\hfill \end{array}$ (3)

模型(3)加入了噪声项，考虑了实际情况，相比较于模型(1)，许多的研究者不考虑突发因素的干扰。由于营养物质的状态是隐藏的，不能直接获得，因此模型很难研究，一些研究者会考虑加入隐马尔可夫过程，对隐含状态提高准确的识别，但还是比较困难的，所以我们考虑运用非线性滤波技术 [6] [7] 获得具有隐藏状态的随机营养物质-浮游植物模型的长期行为。

2. 准备知识

在本文中，将使用 ${ℝ}_{+}:=\left[0,\infty \right),{ℝ}_{+}^0:=\left[0,\infty \right),{ℝ}_{+}^2:=\left[0,\infty \right)\times \left[0,\infty \right)$ ，以及 ${ℝ}_{+}^{2,0}:=\left(0,\infty \right)\times \left(0,\infty \right)$ 。设 $\left(\Omega ,\mathcal{F},{\left\{\mathcal{F}\right\}}_{t\ge 0},\mathbb{P}\right)$ 具有满足通常条件滤的完备概率空间，并且 $B_1\left(t\right),B_2\left(t\right)$ 和 $W\left(t\right)$ 是相互独立的标准布朗运动。信号过程 $\alpha \left(t\right)$ 在 $\left[\text{0,1}\right]$ 中取值，其被假定是一个自适应的随机过程，且与 $B_1\left(t\right),B_2\left(t\right)$ 和 $W\left(t\right)$ 相独立。 $\mathcal{M}$ 表示在 $\left(\left[0,1\right],\mathcal{B}\left(\left[0,1\right]\right)\right)$ 上被赋予弱拓扑的概率测度空间， $C\left[0,1\right]$ 表示在 $\left[\text{0,1}\right]$ 上所有实值连续的函数空间。对任何函数 $l\in C\left[0,1\right]$ 和 $\mu \in \mathcal{M}$ ，设

$\mu \left(l\right):={\displaystyle {\int }_0^{1}l}\left(x\right)\mu \left(\text{d}x\right).$

考虑假设中的精确值 $\alpha \left(t\right)$ 不可用，只有噪声观测可用。 $\alpha \left(t\right)$ 的观测过程 $r\left(t\right)$ 如下

$\text{d}r\left(t\right)=\rho \left(\alpha \left(t\right)\right)\text{d}t+\text{d}W\left(t\right),r\left(0\right)=0,$ (4)

其中 $\rho :\left[0,1\right]\to ℝ$ 为连续函数。设 ${\mathcal{F}}_t^r:=\varrho \left\{r\left(s\right):0\le s\le t\right\}\vee \varrho \left(\alpha \left(0\right)\right)$ ，其中 $\vee$ 表示由一些 $\varrho$ -代数并集生成的最小 $\varrho$ -代数。设 $\pi \prod (\cdot )\in \mathcal{M}$ 是在给定观测值 $r\left(t\right)$ 的条件下， $\alpha \left(t\right)$ 的条件分布和初始数据，即

${\Pi }_t\left(A\right)=\mathbb{P}\left[\alpha \left(t\right)\in A|{\mathcal{F}}_t^r\right],A\in \mathcal{B}\left(\left[0,1\right]\right).$

则 ${\Pi }_t(\cdot )$ 称为非线性滤波器。

进一步，介绍Fujisaki-Kallianpuru-Kunita的结果 [6] ，涉及到了非线性滤波器 ${\Pi }_t(\cdot )$ 的微分方程。定义 $\xi \left(t\right)=r\left(t\right)-{\displaystyle {\int }_0^t{\Pi }_s}\left(\rho \right)\text{d}s,$

其中过程 $\xi \left(t\right)$ 是一维维纳过程。此外， $\varrho \left\{\xi \left(t_2\right)-\xi \left(t_1\right):t_2\ge t_1\ge t\right\}$ 和 ${\mathcal{F}}_t^r$ 对于所有 $t\ge 0$ 是独立的。如果 $\alpha \left(t\right)$ 是具有无穷小生成元 的马尔可夫过程, ${\Pi }_t(\cdot )$ 为式(5)的解。

${\Pi }_t\left(l\right):={\Pi }_0\left(l\right)+{\displaystyle {\int }_0^t{\Pi }_s}\left(Al\right)\text{d}s+{\displaystyle {\int }_0^t\left({\Pi }_s\left(l\rho \right)-{\Pi }_s\left(l\right){\Pi }_s\left(\rho \right)\right)\text{d}\xi }\left(s\right),\forall l\in \mathcal{D}\left(A\right).$ (5)

为了讨论下一节，需要建立相关遍历性。把 ${\Pi }_t(\cdot )$ 当作一个取值在 $\mathcal{M}$ 上的随机过程，利用 ${\Pi }_t(\cdot )$ 的连续可测的修正。

在只观察到 $\alpha \left(t\right)$ 的噪声项的前提下，继续研究系统(3)，使用非线性滤波器 ${\Pi }_t(\cdot )$ ， ${\Pi }_t(\cdot )$ 具有给定观测过程 $r\left(t\right)$ 的信息。考虑了系统(6)

$\{\begin{array}{l}\text{d}N\left(t\right)=\left[D{N}^0-DN\left(t\right)-{\displaystyle {\int }_0^{1}P}\left(t\right)y\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)-P\left(t\right){\displaystyle {\int }_0^{1}x}g\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)\right]\text{d}t+{\varrho }_{1}N\left(t\right)\text{d}{B}_1\left(t\right),\\ \text{d}P\left(t\right)=[-D_{1}P\left(t\right)-\frac{e_1{\sigma }_{1}P\left(t\right)}{1+h{e}_1{\sigma }_{1}P\left(t\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(t\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(t\right)\right)}\right)\left(\gamma -P\left(t\right)\right)+{\displaystyle {\int }_0^{1}P}\left(t\right)y\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)\\ \begin{array}{c}\\ \end{array}+P\left(t\right){\displaystyle {\int }_0^{1}x}g\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)]\text{d}t+{\varrho }_{2}P\left(t\right)\text{d}{B}_2\left(t\right),\end{array}$ (6)

其中

$\begin{array}{l}{\Pi }_t\left(A\right)=\mathbb{P}\left[\alpha \left(t\right)\in A|{\mathcal{F}}_t^r\right],\forall A\in \mathcal{B}\left(\left[0,1\right]\right),\\ \text{d}r\left(t\right)=\rho \left(\alpha \left(t\right)\right)\text{d}t+\text{d}W\left(t\right),r\left(0\right)=0.\end{array}$

${\mathbb{P}}_{u,\upsilon ,\pi }$ 和 ${\mathbb{E}}_{u,\upsilon ,\pi }$ 分别表示初始值为 $N\left(0\right)=u,P\left(0\right)=\upsilon ,{\Pi }_0=\pi$ 和 $\alpha \left(0\right)$ 的分布所对应的概率和期望。

假设2.1以下条件成立：

· 函数 $y:\left[0,1\right]\times {ℝ}_{+}^2\to {ℝ}_{+}$ 是非负的， $y\left(x,0,p\right)=0,\forall x\in \left[0,1\right],p\ge 0$ 。此外，y是利普希兹连续的，即存在一个正常数 $L_1$ 使得对所有的 $x_1,x_2\in \left[0,1\right],n_1,n_2,p_1,p_2\ge 0$ ，

$\left|y\left(x_1,n_1,p_1\right)-y\left(x_2,n_2,p_2\right)\right|\le L_1\left(\left|x_1-x_2\right|+\left|n_1-n_2\right|+\left|p_1-p_2\right|\right).$

· 函数 $g:\left[0,1\right]\times {ℝ}_{+}^2\to {ℝ}_{+}$ 满足 $g\left(x,0,p\right)=0$ ，g是利普希兹连续的，具有利普希兹常数 $L_2$ ，即对所有的 $x_1,x_2\in \left[0,1\right],n_1,n_2,p_1,p_2\ge 0$ ，

$\left|g\left(x_1,n_1,p_1\right)-g\left(x_2,n_2,p_2\right)\right|\le L_2\left(\left|x_1-x_2\right|+\left|n_1-n_2\right|+\left|p_1-p_2\right|\right).$

· 对每一个 $x\in \left[0,1\right]$ ，函数 $g\left(x,\cdot ,0\right)$ 和 $y\left(x,\cdot ,0\right)$ 是非递减的。

假设2.2 $\alpha \left(t\right)$ 是马尔可夫费勒过程，有唯一不变测度 ${\mu }^{*}$ 和

${\Vert P\left(t,x,\cdot \right)-{\mu }^{*}(\cdot )\Vert }_{TV}=0.$

其中 $P\left(t,x,\cdot \right)$ 是转移概率和 ${\Vert \cdot \Vert }_{TV}$ 是总变异范数。

命题2.1 [8] 假设在紧可分Hausdorff空间中赋值的 $\alpha \left(t\right)$ 是具有半群 $P\left(t\right)$ 的马尔可夫费勒过程，该过程有唯一不变测度 ${\mu }^{*}$ 和

$\underset{t\to \infty }{\lim \sup }{\displaystyle \int \left|P_{t}l\left(x\right)-{\mu }^{*}\left(l\right)\right|\mu \left(\text{d}x\right)}=0,\forall l\in C\left(\left[0,1\right]\right).$

过程 ${\Pi }_t(\cdot )$ 是有唯一不变测度 ${\Phi }^{*}$ 的 $\mathcal{M}$ 值马尔可夫费勒过程， ${\mu }^{*}$ 为 ${\Phi }^{*}$ 的重心，即，

${\mu }^{*}\left(l\right):={\displaystyle {\int }_{\mathcal{M}}\nu }\left(l\right){\Phi }^{*}\left(\text{d}\nu \right),\forall l\in C\left[0,1\right].$

在证明非线性滤波的不变测度的唯一性中，需要恒等式(7)

${\displaystyle {\cap }_{t\ge 0}{\mathcal{F}}_{\left[0,\infty \right)}^r\vee \varrho \left\{\alpha \left(s\right):s\ge t\right\}}={\mathcal{F}}_{\left[0,\infty \right)}^r\vee \left({\displaystyle {\cap }_{t\ge 0}\varrho }\left\{\alpha \left(s\right):s\ge t\right\}\right).$ (7)

其中 ${\mathcal{F}}_{\left[0,\infty \right)}^r:={\vee }_{t\ge 0}{\mathcal{F}}_t^r$ 。

命题2.2 在假设2.2下，过程 ${\Pi }_t(\cdot )$ 是一个 $\mathcal{M}$ 值马尔可夫费勒过程和有唯一不变测度 ${\Phi }^{*}$ ， ${\mu }^{*}$ 是 ${\Phi }^{*}$ 的重心，即

${\mu }^{*}\left(l\right):={\displaystyle {\int }_{\mathcal{M}}\nu }\left(l\right){\Phi }^{*}\left(\text{d}\nu \right),\forall l\in C\left[0,1\right].$

接下来，讨论灭绝性和持久性的阈值 [9] 。将使用以上讨论的非线性滤波器的遍历性，并结合来自动力系统的李亚普诺夫指数 [10] 。引入一个阈值 $\lambda$ ，表征系统(6)的长期行为。

考虑边界上的方程，当浮游植物不存在时，即

$\text{d}\phi \left(t\right)=\left(D{N}^0-D\phi \left(t\right)\right)\text{d}t+{\varrho }_1\phi \left(t\right)\text{d}{B}_1\left(t\right),\phi \left(0\right)=u\ge 0.$ (8)

通过求解Fokker-Planck方程，方程(8)有唯一的平稳分布 $\hat{\mu }$ ，其密度为

$\frac{b^a}{\Gamma \left(a\right)}{r}^{-\left(a+1\right)}{\text{e}}^{-\frac{b}{r}},r>0.$ (9)

其中 $c_1=D+\frac{{\varrho }_1^2}{2},a=\frac{2c_1}{{\varrho }_{\text{1}}^{\text{2}}},b=\frac{2D{N}^0}{{\varrho }_{\text{2}}^{\text{2}}}$ 和 $\Gamma (\cdot )$ 是伽马函数。通过观察李亚普诺夫指数 $\lim {\sup }_{t\to \infty }\frac{\ln P\left(t\right)}{t}$ 在 $P\left(t\right)$ 很小时，来确定 $P\left(t\right)$ 是否收敛于0。运用伊藤公式得出

$\begin{array}{l}\frac{\ln P\left(t\right)}{t}=\frac{\ln \upsilon }{t}+\frac{{\varrho }_2{B}_2\left(t\right)}{t}-c_2-\frac{1}{t}{\displaystyle {\int }_0^t\frac{e_1{\sigma }_1}{1+h{e}_1{\sigma }_{1}P\left(s\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(s\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(s\right)\right)}\right)}\left(\gamma -P\left(s\right)\right)\text{d}s\\ +\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s,\end{array}$ (10)

其中 $c_2=D_1+\frac{{\varrho }_2^2}{2}$ 。 $\lim {\sup }_{t\to \infty }\frac{\ln P\left(t\right)}{t}<0$ 意味着 ${\lim }_{t\to \infty }P\left(t\right)=0$ 。因此，如果 $P\left(t\right)$ 很小，那么提供 $N\left(0\right)=\phi \left(0\right)$ ， $N\left(t\right)$ 就接近于 $\phi \left(t\right)$ ，同时有

$\frac{1}{t}{\displaystyle {\int }_0^t\frac{e_1{\sigma }_1}{1+h{e}_1{\sigma }_{1}P\left(s\right)}}\left(1-\frac{e_1{\sigma }_{1}P\left(s\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(s\right)\right)}\right)\left(\gamma -P\left(s\right)\right)\le e_1{\sigma }_1\gamma .$

当t足够大时，有

$\begin{array}{l}-e_1{\sigma }_1\gamma +\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ \approx -e_1{\sigma }_1\gamma +\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s.\end{array}$

从式(10)，由 $\phi \left(t\right)$ 和 ${\Pi }_t(\cdot )$ 的强大数定律，得到 $P_{u,\upsilon }\left(t\right)$ 的李亚普诺夫指数可以近似为

$-c_2-e_1{\sigma }_1\gamma +{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{\mathcal{M}}\left({\displaystyle {\int }_0^{1}y}\left(x,r,0\right)\nu \left(\text{d}x\right)\right)}}{\Phi }^{*}\left(\text{d}\nu \right)\hat{\mu }\left(\text{d}r\right)+{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{\mathcal{M}}\left({\displaystyle {\int }_0^{1}x}g\left(x,r,0\right)\nu \left(\text{d}x\right)\right)}}{\Phi }^{*}\left(\text{d}\nu \right)\hat{\mu }\left(\text{d}r\right).$ (11)

由于 ${\mu }^{*}$ 是 ${\Phi }^{*}$ 的重心， $P\left(t\right)$ 的李亚普诺夫指数近似为

$-c_2-e_1{\sigma }_1\gamma +{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}y}}\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right)+{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}x}}g\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right).$

因此，将阈值 $\lambda$ 定义为

$\lambda :=-c_2-e_1{\sigma }_1\gamma +{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}y}}\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right)+{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}x}}g\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right).$

3. 解的存在唯一性和费勒过程

本小节，主要讨论具有隐藏状态的随机营养物质–浮游植物模型(3)解的存在唯一性和费勒过程。

定理3.1对于任意 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^2\times \mathcal{M}$ ，则系统(6)存在唯一全局解，其初始值为 $\left(u,\upsilon ,\pi \right)$ ，且随机过程 $\left\{\left(N\left(t\right),P\left(t\right),{\Pi }_t\right),t\ge 0\right\}$ 是马尔科夫过程。

证明：首先证明系统(6)解的存在唯一性。假设 $y\left(n,p\right)$ 是利普希兹连续的，但系统(6)中的系数 $py\left(n,p\right)$ 一般不是全局的利普希兹。因为系统(6)的系数是局部利普希兹连续的，系统有唯一的解 $\left(N\left(t\right),P\left(t\right)\right)$ 与初始值 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^2\times \mathcal{M}$ [11] ，需定义最大区间 $t\in \left[0,{\tau }_e\right),{\tau }_e:=\inf \left\{t\ge 0:N\left(t\right)\vee P\left(t\right)=\infty \right\}$ 和约定 $\inf \varnothing =\infty$ 。设

${\tau }_k=\inf \left\{t\ge 0:N\left(t\right)\vee P\left(t\right)>k\right\},$

则 ${\tau }_e={\lim }_{t\to \infty }{\tau }_k$ 。考虑 $V_1\left(n,p\right)=n+p$ ，则从 $\mathcal{L}{V}_1$ 的定义有

$\begin{array}{c}\mathcal{L}{V}_1\left(n,p,\pi \right)=D{N}^0-Dn-D_{1}p-\frac{e_1{\sigma }_{1}p}{1+h{e}_1{\sigma }_{1}p}\left(1-\frac{e_1{\sigma }_{1}p}{4G_1\left(1+h{e}_1{\sigma }_{1}p\right)}\right)\left(\gamma -p\right)\\ \le D{N}^0+\frac{e_1{\sigma }_{1}p}{1+h{e}_1{\sigma }_{1}p}\left(1-\frac{e_1{\sigma }_{1}p}{4G_1\left(1+h{e}_1{\sigma }_{1}p\right)}\right)p\\ \le D{N}^0+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p},\forall \left(n,p,\pi \right)\in {ℝ}_{+}^2\times \mathcal{M}.\end{array}$

运用伊藤公式并取期望，则

${\mathbb{E}}_{u,\upsilon ,\pi }{V}_1\left(N\left({\tau }_k\wedge t\right),P\left({\tau }_k\wedge t\right)\right)\le V_1\left(u,\upsilon \right)+\left(D{N}^0+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p}\right)t.$

由马尔可夫不等式，得出

$\begin{array}{c}\mathbb{P}\left\{{\tau }_k<t\right\}\le {\mathbb{P}}_{u,\upsilon ,\pi }\left\{V_1\left(N\left({\tau }_k\wedge t\right),P\left({\tau }_k\wedge t\right),\alpha \left({\tau }_k\wedge t\right)\right)\ge k\right\}\\ \le \frac{V_1\left(u,\upsilon \right)+\left(D{N}^0+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p}\right)t}{k}\to 0\text{as}k\to \infty .\end{array}$

因此，对于所有 $t>0$ ，有 ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{{\tau }_e\le t\right\}=0$ 或 ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{{\tau }_e>t\right\}=1$ 。因此， ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{{\tau }_e=\infty \right\}=1$ ，系统(6)有唯一全局连续的解。

继续证明马尔科夫性质。由于 ${\Pi }_t$ 是一个马尔可夫过程并且与 $B_1\left(t\right)$ 和 $B_2\left(t\right)$ 相互独立，对于过程 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 的马尔可夫性质遵循标准论证 [11] 。

接下来，利用李亚普诺夫函数，得出 $N\left(t\right)$ 和 $P\left(t\right)$ 的矩估计，定义 ${\varrho }_{\text{*}}^{\text{2}}:=\max \left\{{\varrho }_{\text{1}}^{\text{2}},{\varrho }_{\text{2}}^{\text{2}}\right\}$ 。

引理3.1以下结论成立：

(i) 对于任意的 $0<\bar{q}<\frac{2k}{{\varrho }_{*}^2}$ ，有常数 $Q_1$ 使得

$\underset{t\to \infty }{\lim \sup }{\mathbb{E}}_{u,\upsilon ,\pi }{\left(N\left(t\right)+P\left(t\right)\right)}^{1+\bar{q}}\le Q_1,\forall \left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^2\times \mathcal{M}.$

(ii) 对于任意的 $\epsilon >0,H>1,T>0$ ，有 $\bar{H}=\bar{H}\left(\epsilon ,H,T\right)$ 使得

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{\frac{1}{\bar{H}}\le N\left(t\right)\le \bar{H},\forall t\in \left[0,T\right]\right\}\ge 1-\epsilon \text{if}\left(u,\upsilon ,\pi \right)\in \left[H^{-1},H\right]\times \left[0;H\right]\times \mathcal{M},$

和

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{0\le N\left(t\right),P\left(t\right)\le \bar{H},\forall t\in \left[0,T\right]\right\}\ge 1-\epsilon \text{if}\left(u,\upsilon ,\pi \right)\in \left[0,H\right]\times \left[0;H\right]\times \mathcal{M}.$

证明：考虑李亚普诺夫函数 $V_3\left(n,p\right)={\left(n+p\right)}^{1+\bar{q}}$ 。通过直接用微分算子 $\mathcal{L}{V}_3$ 计算和利用假设2.1，得出

$\begin{array}{c}\mathcal{L}{V}_3\left(n,p,\pi \right)=\left(1+\bar{q}\right){\left(n+p\right)}^{\bar{q}}\left[D{N}^0-Dn-D_{1}p-\frac{e_1{\sigma }_{1}p}{1+h{e}_1{\sigma }_{1}p}\left(1-\frac{e_1{\sigma }_{1}p}{4G_1\left(1+h{e}_1{\sigma }_{1}p\right)}\right)\left(\gamma -p\right)\right]\\ +\frac{\bar{q}\left(1+\bar{q}\right)}{2}{\left(n+p\right)}^{\bar{q}-1}\left({\varrho }_1^2{n}^2+{\varrho }_2^2{p}^2\right)\\ \le -\left(1+\bar{q}\right){\left(n+p\right)}^{\bar{q}-1}\left[-\frac{\bar{q}}{2}{\varrho }_{*}^2{\left(n+p\right)}^2-\left(D{N}^0+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p}\right)\left(n+p\right)\right],\end{array}$

其中 $\forall \left(n,p,\pi \right)\in {ℝ}_{+}^2\times \mathcal{M}$ ，设 $0<C_4<\frac{\bar{q}\left(1+\bar{q}\right)}{2}{\varrho }_{*}^2$ 。通过计算，得出

$C_5=\underset{\left(n,p,\pi \right)\in {ℝ}_{+}^{{}_2}\times \mathcal{M}}{\sup }\left\{\mathcal{L}{V}_3\left(n,p,\pi \right)+C_4{V}_3\left(n,p\right)\right\}<\infty .$

则

$\mathcal{L}{V}_3\le C_5-C_4{V}_3.$ (12)

运用系统(6)解的存在性 [12] ，证明引理的第(i)部分。第(ii)部分的证明源于第(i)部分和标准论证 [12] 。

定理3.2过程 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 是系统(6)的一个强马尔可夫和费勒过程。有 ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{N\left(t\right)>0,t>0\right\}=1$ 和 ${\mathbb{P}}_{u,0,\pi }\left\{P\left(t\right)=0,t>0\right\}=1,{\mathbb{P}}_{u,\upsilon ,\pi }\left\{P\left(t\right)>0,t>0\right\}=1,\upsilon >0$ 。

证明：如果系统(6)的系数是全局利普希兹，则系统(6)的解是一个齐次强马尔可夫和费勒过程 [12] [13] 。在 $\left[0,1\right]$ 中，弱拓扑的概率测度空间 $\mathcal{M}$ 是由有界的利普希兹度量进行定义的，如下

${\Vert {\pi }_1-{\pi }_2\Vert }_{BL}:=\sup \left\{\left|{\pi }_1\left(l\right)-{\pi }_2\left(l\right)\right|:\Vert l\Vert \le 1,\underset{x\ne r\in \left[0,1\right]}{\sup }\frac{\left|l\left(x\right)-l\left(r\right)\right|}{\left|x-r\right|}\le 1\right\}.$

因此，通过引理3.1的结果，系统(6)系数的局部利普希兹性质和截断论证 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 是齐次强马尔可夫和费勒过程 [14] 。

接下来，建立解的正性。首先，假设 $u,\upsilon >0$ 。考虑李亚普诺夫函数 $V_2:{ℝ}_{+}^2\to {ℝ}_{+}$

$V_2=\left(n,p\right)=\left(n-1-\ln n\right)+\left(p-1-\ln p\right).$

通过计算，有

$\begin{array}{c}\mathcal{L}{V}_2\left(n,p,\pi \right)=\left(1-\frac{1}{n}\right)\left(D{N}^0-Dn-py\left(x,n,p\right)-p{\displaystyle {\int }_0^{1}x}g\left(x,n,p\right)\pi \left(\text{d}x\right)\right)+\frac{{\varrho }_1^2{n}^2}{2n^2}\\ +\left(1-\frac{1}{p}\right)[-D_{1}p-\frac{e_1{\sigma }_{1}p}{1+h{e}_1{\sigma }_{1}p}\left(1-\frac{e_1{\sigma }_{1}p}{4G_1\left(1+h{e}_1{\sigma }_{1}p\right)}\right)\left(\gamma -p\right)\\ \begin{array}{c}\\ \end{array}+py\left(x,n,p\right)+p{\displaystyle {\int }_0^{1}x}g\left(x,n,p\right)\pi \left(\text{d}x\right)]+\frac{{\varrho }_2^2{p}^2}{2p^2}.\end{array}$

由假设2.1可知 $y\left(x,n,p\right)=\left|y\left(x,n,p\right)-y\left(x,0,p\right)\right|\le L_{1}n$ 和 $g\left(x,n,p\right)=\left|g\left(x,n,p\right)-g\left(x,0,p\right)\right|\le L_{2}n$ 。则

$\begin{array}{c}\mathcal{L}{V}_2\left(n,p\right)\le C_1+\frac{py\left(n,p\right)}{n}+\frac{p{\displaystyle {\int }_0^{1}g}\left(x,n,p\right)\pi \left(\text{d}x\right)}{n}+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p}\\ \le C_1+\left(L_1+L_2\right)\left(n+p\right)+\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p},\end{array}$

令 $\frac{e_1{\sigma }_1{p}^2}{1+h{e}_1{\sigma }_{1}p}=0$ ，假设 $C_2=L_1+L_2+1$ 和 $C_3=C_1+2C_2\ln C_2+2C_2$ ，则 $C_1=D{N}^0+D+\frac{{\varrho }_1^2}{2}+D_1+e_1{\sigma }_1\gamma +\frac{{\varrho }_2^2}{2}$ 。得出

$\begin{array}{c}\mathcal{L}{V}_2\left(n,p,\pi \right)-C_2{V}_2\left(n,p\right)\le C_1-n-p+C_2\left(\ln n+\ln p\right)+2C_2\\ \le C_1+2C_2\ln C_2+2C_2=C_3.\end{array}$ (13)

对 $k>1$ ，定义

$\begin{array}{l}\eta =\inf \left\{t\ge 0:N\left(t\right)\wedge P\left(t\right)\le 0\right\},\\ {\eta }_k=\inf \left\{t\ge 0:N\left(t\right)\wedge P\left(t\right)<\frac{1}{k}\right\}.\end{array}$

得到 $\eta ={\lim }_{k\to \infty }{\eta }_k$ 。另外，通过使用与上面相同的论证，从而由式(13)，得出

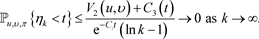
因此， ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{{\eta }_{\infty }=\infty \right\}=1$ ，得出

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{N\left(t\right)>0:t>0\right\}={\mathbb{P}}_{u,\upsilon ,\pi }\left\{P\left(t\right)>0:t>0\right\}=1,\forall u,\upsilon >0.$ (14)

如果 $u>0,\upsilon =0$ ，则 ${\mathbb{P}}_{u,\upsilon ,\pi }\left\{N\left(t\right)>0:t>0\right\}=1$ 可以类似地证明。此外， ${\mathbb{P}}_{u,0,\pi }\left\{P\left(t\right)=0:t>0\right\}=1$ 是明显的。

考虑 $u=0$ 和 $\upsilon \ge 0$ 的情况，证明 $N\left(t\right)$ 的正性。设 $\epsilon >0$ 足够小，使得

$D{N}^0-D\tilde{u}-\tilde{\upsilon }\underset{x\in \left[0,1\right]}{\sup }\left(y\left(x,\tilde{u},\tilde{\upsilon }\right)+g\left(x,\tilde{u},\tilde{\upsilon }\right)\right)\ge \frac{D{N}^0}{2},\sqrt{a^2+b^2}$ (15)

对于任何 $\left(\tilde{u},\tilde{\upsilon }\right)\in {ℝ}^2$ 满足 $\tilde{u}+\left|\tilde{\upsilon }-\upsilon \right|<\epsilon$ 。由假设2.1，存在一个 $\epsilon$ ，设

${\tilde{\tau }}_1=\inf \left\{t>0:N\left(t\right)+\left|P\left(t\right)-\upsilon \right|\ge \epsilon \right\}.$

由 $\left(N\left(t\right),P\left(t\right)\right)$ 的连续性，可知 ${\mathbb{P}}_{0,\upsilon ,\pi }\left\{{\tilde{\tau }}_1>0\right\}=1$ 。由式(15)可知，如果 $t\in \left(0,{\tilde{\tau }}_1\right]$ ，有

$D{N}^0-DN\left(t\right)-P\left(t\right){\displaystyle {\int }_0^{1}y}\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)-P\left(t\right){\displaystyle {\int }_0^{1}x}g\left(x,N\left(t\right),P\left(t\right)\right){\Pi }_t\left(\text{d}x\right)>0.$

从常数变分公式 [12] 可知

${\mathbb{P}}_{0,\upsilon ,\pi }\left\{N\left(t\right)>0,t\in \left(0,{\tilde{\tau }}_1\right]\right\}=1,$

结合式(14)和 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 的强马尔可夫性质，得出

${\mathbb{P}}_{0,\upsilon ,\pi }\left\{N\left(t\right)>0,t\in \left(0,\infty \right)\right\}=1.$

定理证明完毕。

4. 长期行为

本小节，主要讨论具有隐藏状态的随机营养物质–浮游植物模型(3)解的持久性和灭绝性。

引理4.1对于任意 $T,H>1,\epsilon >0,\theta >0$ ，有 $\delta =\delta \left(H,T,\epsilon ,\theta \right)$ ，使得

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{{\tau }_{\theta }\ge T\right\}\ge 1-\epsilon ,\forall \left(u,\upsilon ,\pi \right)\in \left[0,H\right]\times \left(0,\delta \right]\times \mathcal{M},$

其中 ${\tau }_{\theta }=\inf \left\{t\ge 0:P_{u,\upsilon }\left(t\right)>\theta \right\}$ 。

证明：通过指数鞅不等式 [12] ，有 ${\mathbb{P}}_{u,\upsilon ,\pi }\left({\Omega }_1\right)\ge 1-\frac{\epsilon }{2}$ ，其中

${\Omega }_1=\left\{{\varrho }_2{B}_2\left(t\right)\le \frac{{\varrho }_2^{2}t}{2}+\ln \frac{2}{\epsilon },\forall t\ge 0\right\}.$

由引理3.1第(ii)部分，存在一个 $\bar{H}=\bar{H}\left(T,H,\epsilon \right)$ ，使得 ${\mathbb{P}}_{u,\upsilon ,\pi }\left({\Omega }_2\right)\ge 1-\frac{\epsilon }{2}$ ，其中

${\Omega }_2=\left\{0\le N\left(t\right),P\left(t\right)\le \bar{H},\forall t\in \left[0,T\right]\right\}.$

将伊藤公式应用于系统(6)

$\begin{array}{c}\ln P\left(t\right)=\ln \upsilon -c_{2}t-{\displaystyle {\int }_0^t\frac{e_1{\sigma }_1}{1+h{e}_1{\sigma }_{1}P\left(s\right)}\left(1-\frac{e_1{\sigma }_{1}P\left(s\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(s\right)\right)}\right)}\left(\gamma -P\left(s\right)\right)\text{d}s\\ +{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N_{u,\upsilon }\left(s\right),P_{u,\upsilon }\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\varrho }_2{B}_2\left(t\right).\end{array}$ (16)

因此，对于任何 $\left(n,p,\pi \right)\in \left[0,H\right]\times \left(0,H\right]\times \mathcal{M}$ 和 $\omega \in {\Omega }_1\cap {\Omega }_2$ ，由(16)和y、g的利普希兹连续性，有

$\ln P\left(t\right)<\ln \upsilon -D_{1}T-e_1{\sigma }_1\gamma T+T\left(2L_1\bar{H}+2L_2\bar{H}\right)+\ln \frac{2}{\epsilon },\forall t\in \left[0,T\right].$

此时，可以选择一个足够小的 $\delta =\delta \left(H,T,\epsilon ,\theta \right)<H$ ，可以得出 $\left(n,p,\pi \right)\in \left[0,H\right]\times \left(0,\delta \right]\times \mathcal{M}$ 和 $0\le t\le T,\ln P\left(t\right)<\ln \theta ,\forall \omega \in {\Omega }_1\cap {\Omega }_2$ 。证明完毕。

命题4.1对任何 $0<\epsilon <\min \left\{\frac{1}{5},-\frac{\lambda }{5}\right\}$ 和 $H>1$ ，存在 $\hat{\delta }=\hat{\delta }\left(\epsilon ,H\right)\in \left(0,H^{-1}\right)$ ，使得

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{\underset{t\to \infty }{\lim \sup }\frac{\ln P\left(t\right)}{t}=\lambda \right\}\ge 1-4\epsilon ,\forall \left(u,\upsilon ,\pi \right)\in \left[H^{-1};H\right]\times \left(0;\hat{\delta }\right]\times {\mathcal{M}}_{{\Phi }^{*}}.$

证明：设 ${\theta }_0={\theta }_0\left(\epsilon \right)<\frac{\epsilon }{L_1+L_2}\wedge \frac{D}{L_1+L_2}$ 使得

$\frac{D{N}^0+{\theta }_0\left(L_1+L_2+L_1{\theta }_0+L_2{\theta }_0\right)}{D-\left(L_1+L_2\right){\theta }_0}-\frac{D{N}^0}{D}<\frac{\epsilon }{L_1+L_2}.$ (17)

考虑下面的随机微分方程(18)

$\text{d}\bar{\phi }\left(t\right)=\left(\bar{D}\overline{N^0}-\bar{D}\bar{\phi }\left(t\right)\right)\text{d}t+{\varrho }_1\bar{\phi }\left(t\right)\text{d}{B}_1\left(t\right),$ (18)

其中 $\bar{D}\overline{N^0}=D{N}^0+L_1+L_2+L_1{\theta }_0+L_2{\theta }_0,\bar{D}=D-\left(L_1+L_2\right){\theta }_0>0$ 。如果 $\phi \left(0\right)=\bar{\phi }\left(0\right)$ ，由比较原理，可知 $\phi \left(t\right)\le \bar{\phi }\left(t\right),t\ge 0a.s.$ 再由强大数定律得出

$\begin{array}{l}\underset{t\to \infty }{\lim }\frac{1}{t}|{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ -{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s-{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s|\\ \le \underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_0^t\left(L_1+L_2\right)}\left(\bar{\phi }\left(s\right)-\phi \left(s\right)\right)\text{d}s\\ =\left(L_1+L_2\right)\left(\frac{\bar{D}\overline{N^0}}{\bar{D}}-\frac{D{N}^0}{D}\right)a.s.\end{array}$ (19)

结合式(17)和(19)，得出

$\begin{array}{l}\underset{t\to \infty }{\lim }\frac{1}{t}|{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ -{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s-{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s|<\epsilon a.s.\end{array}$ (20)

因此，存在 $T_1^{*}=T_1^{*}\left(\epsilon \right)$ ，使得 $\mathbb{P}\left({\Omega }_3\right)>1-\epsilon$ ，其中

$\begin{array}{l}{\Omega }_3:=\{|\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ -\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s-\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s|<2\epsilon ,\forall t\ge T_1^{*}\}.\end{array}$

由 $\lambda$ 的定义和 $\phi \left(t\right),{\Pi }_t$ 的遍历性，得出

${\mathbb{P}}_{H,\pi }\left\{-c_2-e_1{\sigma }_1\gamma +\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s=\lambda \right\}=1,$

其中 ${\mathbb{P}}_{H,\pi }$ 表示 $\left(\phi \left(t\right),{\Pi }_t\right)$ 的初始值。因此，存在 $T_2^{*}=T_2^{*}\left(H,\epsilon \right)>1$ 使得 ${\mathbb{P}}_{H,\pi }\left({\Omega }_4\right)\ge 1-\epsilon$ ，其中

${\Omega }_4=\left\{-c_2-e_1{\sigma }_1\gamma +\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s+\frac{1}{t}{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\text{d}s\le \lambda +\epsilon ,\forall t\ge T_2^{*}\right\}.$

鉴于解的唯一性，对所有 $u\in \left[0,H\right]$ ，有 ${\phi }_u\left(s\right)\le {\phi }_H\left(s\right),s\ge 0a.s.$ 其中 $\phi \left(s\right)$ 的下标表示初始值 $\phi \left(0\right)$ 。则对所有 $\left(u,\pi \right)\in \left[0,H\right]\times {\mathcal{M}}_{{\Phi }^{*}}$ ，有 ${\mathbb{P}}_{u,\pi }\left({\Omega }_4\right)\ge 1-\epsilon$ 。

由 ${\lim }_{t\to \infty }\frac{B_2\left(t\right)}{t}=0a.s.$ 有 $T_3^{*}=T_3^{*}\left(\epsilon \right)>1$ 使得 $\mathbb{P}\left({\Omega }_5\right)\ge 1-\epsilon$ ，其中

${\Omega }_5=\left\{{\sigma }_2\frac{B_2\left(t\right)}{t}<\epsilon ,\forall t\ge T_3^{*}\right\}.$

令 $T=\max \left\{T_1^{*},T_2^{*},T_3^{*}\right\}$ 。由引理4.1，有 $\hat{\delta }=\hat{\delta }\left(\epsilon ,H\right)<{\theta }_0$ ，使得 $\left(u,\upsilon ,\pi \right)\in \left[0,H\right]\times \left(0,\hat{\delta }\right]\times \mathcal{M}$ ， ${\mathbb{P}}_{u,\upsilon ,\pi }\left({\Omega }_6\right)\ge 1-\epsilon$ ，其中

${\Omega }_6=\left\{{\tau }_{{\theta }_0}\ge T\right\}.$

现在，由式(20)得出 $\forall \left(u,\upsilon ,\pi \right)\in \left[0,H\right]\times \left(0,\delta \right]\times {\mathcal{M}}_{{\Phi }^{*}}$ 。在 ${\displaystyle {\cap }_{j=3}^6{\Omega }_j}$ 中，对于所有的 $t\in \left[T,{\tau }_{{\theta }_0}\right]$ ，有

$\begin{array}{c}\ln P\left(t\right)=\ln \upsilon -c_{2}t-e_1{\sigma }_1\gamma t+{\varrho }_2{B}_2\left(t\right)+{\displaystyle {\int }_0^t\left({\displaystyle {\int }_0^{1}y}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\right)\text{d}s}\\ =\ln \upsilon -c_{2}t-e_1{\sigma }_1\gamma t+{\varrho }_2{B}_2\left(t\right)+{\displaystyle {\int }_0^t\left({\displaystyle {\int }_0^{1}y}\left(x,N\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,N\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\right)\text{d}s}\\ +{\displaystyle {\int }_0^t({\displaystyle {\int }_0^{1}y}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)}\\ -{\displaystyle {\int }_0^{1}y}\left(x,N\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)-{\displaystyle {\int }_0^{1}x}g\left(x,N\left(s\right),0\right){\Pi }_s\left(\text{d}x\right))\text{d}s\end{array}$

$\begin{array}{c}\le \ln \upsilon -c_{2}t-e_1{\sigma }_1\gamma t+{\displaystyle {\int }_0^t\left({\displaystyle {\int }_0^{1}y}\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,\bar{\phi }\left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\right)\text{d}s}\\ +\epsilon t+\left(L_1+L_2\right){\displaystyle {\int }_0^{t}P}\left(s\right)\text{d}s\\ \le \ln \upsilon -c_{2}t-e_1{\sigma }_1\gamma t+3\epsilon t+{\displaystyle {\int }_0^t\left({\displaystyle {\int }_0^{1}y}\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,\phi \left(s\right),0\right){\Pi }_s\left(\text{d}x\right)\right)\text{d}s}\\ \le \ln \upsilon +\left(\lambda +4\epsilon \right)t<\ln \hat{\delta }<\ln {\theta }_0.\end{array}$ (21)

如上所述，当 $P\left(t\right)\le {\theta }_0$ ，有

$\begin{array}{c}P\left(s\right){\displaystyle {\int }_0^{1}x}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\le {\theta }_0\left(g\left(0,0,0\right)+L_2+L_{2}N\left(s\right)+L_{2}P\left(s\right)\right)\\ \le {\theta }_0\left(L_2+L_2{\theta }_0\right)+L_2{\theta }_{0}N\left(s\right),\end{array}$

因此，对所有 $t\in \left[0,{\tau }_{{\theta }_0}\right]$ ，有 $N\left(s\right)\le \bar{\phi }\left(s\right)$ 。

由式(21)的结论，对于 $\omega \in {\displaystyle {\cap }_{j=3}^6{\Omega }_j}$ ，得出 ${\tau }_{{\theta }_0}=\infty$ 。根据式(11)，由 ${\bar{D}}_1>0$ ，式(18)的解有唯一不变测度，记为 $\bar{\mu }$ 。从 $\bar{\phi }\left(t\right)$ 的遍历性得到，对于一些小 $\hat{q}>0$ ，则

$\underset{t\to \infty }{\lim \sup }\frac{1}{t}{\displaystyle {\int }_0^t{N}^{\left(1+\hat{q}\right)}}\left(u\right)\text{d}u\le \underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_0^t{\bar{\phi }}^{\left(1+\hat{q}\right)}}\left(u\right)\text{d}u={\displaystyle \int x^{\left(1+\hat{q}\right)}}\bar{\mu }\left(\text{d}x\right)<\infty .$ (22)

式(22)包含在 ${\displaystyle {\cap }_{j=3}^6{\Omega }_j}$ 中。利用式(22)和 ${\lim }_{t\to \infty }P\left(t\right)=0$ ，以及 $\mathcal{M}$ 的紧密性，随机占有测度

${\tilde{U}}_{u,\upsilon ,\pi }^t(\cdot ):=\frac{1}{t}{\displaystyle {\int }_0^t{1}_{\left\{\left(N\left(s\right),P\left(s\right),{\Pi }_s\right)\in \cdot \right\}}\text{d}s},$

几乎对所有的 $\omega \in {\displaystyle {\cap }_{j=3}^3{\Omega }_j}$ 都是紧密的。在概率为1的情况下， ${\tilde{U}}_{u,\upsilon ,\pi }^t(\cdot )$ 的任何弱极限在 $t\to \infty$ 时是不变的概率测度，其在 $\left[0,\infty \right)\times \left\{0\right\}\times \mathcal{M}$ 上是成立的。因为 $\hat{\mu }\times \delta \times {\Phi }^{*}$ 是 $\left[0,\infty \right)\times \left\{0\right\}\times \mathcal{M}$ 的不变概率测试，其中 $\bar{\phi }$ 是集中在0的狄拉克测度，当 $t\to \infty$ 时，在 $\omega \in {\displaystyle {\cap }_{j=3}^6{\Omega }_j}$ 中，几乎可以肯定 ${\tilde{U}}_{u,\upsilon ,\pi }^t(\cdot )$ 族弱收敛于 $\mu 0\times \delta$ 。从(22)中的弱收敛和一致可积性得出

$\begin{array}{c}\underset{t\to \infty }{\lim }\frac{\ln P\left(t\right)}{t}=\underset{t\to \infty }{\lim }\frac{1}{t}[-D_{1}t-\frac{{\varrho }_2^{2}t}{2}-{\displaystyle {\int }_0^t\frac{e_1{\sigma }_1}{1+h{e}_1{\sigma }_{1}P\left(s\right)}}\left(1-\frac{e_1{\sigma }_{1}P\left(s\right)}{4G_1\left(1+h{e}_1{\sigma }_{1}P\left(s\right)\right)}\right)\left(\gamma -P\left(s\right)\right)\text{d}s\\ +{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s]+\underset{t\to \infty }{\lim }\frac{{\varrho }_2{B}_{2}t}{t}\\ \le -c_2-e_1{\sigma }_1\gamma +\underset{t\to \infty }{\lim }{\displaystyle {\int }_{{ℝ}_{+}^2\times \mathcal{M}}\left[{\displaystyle {\int }_0^{1}y}\left(x,r,p\right)\nu \left(\text{d}x\right)+{\displaystyle {\int }_0^{1}x}g\left(x,r,p\right)\nu \left(\text{d}x\right)\right]{\tilde{U}}_{u,\upsilon ,\pi }^t\left(\text{d}r,\text{d}p,\text{d}\nu \right)}\\ =-c_2-e_1{\sigma }_1\gamma +{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{\mathcal{M}}\left[{\displaystyle {\int }_0^{1}y}\left(x,r,0\right)\nu \left(\text{d}x\right)\right]{\Phi }^{*}\left(\text{d}\nu \right)\hat{\mu }\left(\text{d}r\right)}}+{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{\mathcal{M}}\left[{\displaystyle {\int }_0^{1}x}g\left(x,r,0\right)\nu \left(\text{d}x\right)\right]{\Phi }^{*}\left(\text{d}\nu \right)\hat{\mu }\left(\text{d}r\right)}}\\ =\lambda <0.\end{array}$

几乎对于每一个 $\omega \in {\displaystyle {\cap }_{j=3}^6{\Omega }_j}$ ，有 $\left(u,\upsilon ,\pi \right)\in \left[0,H\right]\times \left(0,\hat{\delta }\right]\times {\mathcal{M}}_{{\Phi }^{*}}$ 。由 $\mathbb{P}\left({\displaystyle {\cap }_{j=3}^6{\Omega }_j}\right)>1-4\epsilon$ ，证明完毕。

定理4.1假设 $\lambda <0$ 。那么对于任意初始点 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^{2,0}\times \mathcal{M}$ ，则吸收养分的浮游植物浓度 $P\left(t\right)$ 以指数的速度趋近于零，即，

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{\underset{t\to \infty }{\lim \sup }\frac{\ln P\left(t\right)}{t}=\lambda \right\}=1,$

和营养物浓度 $N\left(t\right)$ 弱收敛于边界上的解 $\phi \left(t\right)$ 。

证明：设任意的 $\epsilon >0$ 。由命题4.1，过程 $\left(N\left(t\right),P\left(t\right)\right)$ 在 ${ℝ}_{+}^{2,0}$ 中是瞬态的 [14] 。因此，过程 $\left(N\left(t\right),P\left(t\right)\right)$ 在 ${ℝ}_{+}^{2,0}$ 中没有不变概率测度。因此，在 ${ℝ}_{+}^2\times {\mathcal{M}}_{{\Phi }^{*}}$ 上， $\hat{\mu }\times \delta \times {\Phi }^{*}$ 是 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 的唯一不变概率测度。

设H足够大，使 $\hat{\mu }\left(\left(0,H\right)\right)>1-\epsilon$ . 由于引理3.1第(i)部分和 $\mathcal{M}$ 的紧密性，过程 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 是紧密的。因此，占有测度

$U_{u,\upsilon ,\pi }^t(\cdot ):=\frac{1}{t}{\displaystyle {\int }_0^t{\mathbb{P}}_{u,\upsilon ,\pi }\left\{\left(N\left(s\right),P\left(s\right),{\Pi }_s\right)\in \cdot \right\}\text{d}s},$

在 ${ℝ}_{+}^2\times \mathcal{M}$ 上是紧密的。当 $t\to \infty$ 时， $U_{u,\upsilon ,\pi }^t$ 的任何弱收敛一定是过程 $\left(N\left(s\right),P\left(s\right),{\Pi }_s\right)$ 的不变概率测度 [15] ，有 $U_{u,\upsilon ,\pi }^t$ 弱收敛于 $\hat{\mu }\times \delta \times {\Phi }^{*}$ 。因此，对任何 $\delta >0$ ，存在 $\hat{T}>0$ 使得

$U_{u,\upsilon ,\pi }^{\hat{T}}(\cdot )\left(\left(0,H\right)\times \left(0,\delta \right)\times {\mathcal{M}}_{{\Phi }^{*}}\right)>1-\epsilon ,$

或

$\frac{1}{\hat{T}}{\displaystyle {\int }_0^{\hat{T}}{\mathbb{P}}_{u,\upsilon ,\pi }}\left\{\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)\in \left(0,H\right)\times \left(0,\delta \right)\times {\mathcal{M}}_{{\Phi }^{*}}\right\}\text{d}t>1-\epsilon .$

则有

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{\hat{\tau }\le \hat{T}\right\}>1-\epsilon ,$

其中 $\hat{\tau }=\inf \left\{t\ge 0:\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)\in \left(0,H\right)\times \left(0,\delta \right)\times {\mathcal{M}}_{{\Phi }^{*}}\right\}$ 。通过利用强马尔可夫性质和命题4.1，有

${\mathbb{P}}_{u,\upsilon ,\pi }\left\{\underset{t\to \infty }{\lim }\frac{\ln P\left(t\right)}{t}\le \lambda +4\epsilon \right\}\ge 1-\epsilon$

对任何 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^{2,*}\times \mathcal{M}$ ，任意的 $\epsilon >0$ ， $P\left(t\right)$ 收敛成立。由于 $P\left(t\right)$ 指数快速收敛到0，则 $N\left(t\right)$ 收敛到 $\phi \left(t\right)$ 。

定义4.1对于任何初始值 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^{2,0}\times \mathcal{M}$ ，系统(6)是持久性的。

$\underset{t\to \infty }{\lim \inf }\frac{1}{t}{\displaystyle {\int }_0^t{\mathbb{E}}_{u,\upsilon ,\pi }}N\left(s\right)\text{d}s>0,\underset{t\to \infty }{\lim \inf }\frac{1}{t}{\displaystyle {\int }_0^t{\mathbb{E}}_{u,\upsilon ,\pi }}P\left(s\right)\text{d}s>0.$

定理4.2假设 $\lambda >0$ 。则对于任意初始值 $\left(u,\upsilon ,\pi \right)\in {ℝ}_{+}^{2,0}\times \mathcal{M}$ ，系统(6)是持久的。

证明：首先证明 $\left(N\left(t\right),P\left(t\right),{\Pi }_t\right)$ 的所有不变测度集中在 ${ℝ}_{+}^{2,0}\times \mathcal{M}$ 上，利用反证法，假设 $\left(N\left(t\right),P\left(t\right)\right)$ 在 ${ℝ}_{+}^{2,0}$ 上没有不变测度。因此，在 ${ℝ}_{+}^{2,*}$ 上没有不变测度，因为根据定理3.1可知，从 ${ℝ}_{+}^{2,*}$ 开始的解将进入并停在 ${ℝ}_{+}^{2,0}$ 中。因此，在 ${ℝ}_{+}^2\times \mathcal{M}$ 上的边界 ${ℝ}_{+}\times \left\{0\right\}\times \mathcal{M}$ 上的唯一不变测度 $\hat{\mu }\times \delta \times {\Phi }^{*}$ 是过程 $\left(N\left(t\right),P\left(t\right),\Pi \left(t\right)\right)$ 的唯一不变测度，则有

$\begin{array}{l}\underset{t\to \infty }{\lim }\frac{1}{t}{\mathbb{E}}_{u,\upsilon ,\pi }{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ ={\displaystyle {\int }_{{ℝ}_{+}^2\times \mathcal{M}}{\displaystyle {\int }_0^{1}y}}\left(x,r,i\right)\hat{\mu }\left(\text{d}r\right)\delta \left(\text{d}i\right){\Phi }^{*}\left(\text{d}\nu \right)\\ ={\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}y}}\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right).\end{array}$ (23)

和

$\begin{array}{l}\underset{t\to \infty }{\lim }\frac{1}{t}{\mathbb{E}}_{u,\upsilon ,\pi }{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ ={\displaystyle {\int }_{{ℝ}_{+}^2\times \mathcal{M}}{\displaystyle {\int }_0^{1}x}}g\left(x,r,i\right)\nu \left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right)\delta \left(\text{d}i\right){\Phi }^{*}\left(\text{d}\nu \right)\\ ={\displaystyle {\int }_{{ℝ}_{+}\times \mathcal{M}}{\displaystyle {\int }_0^{1}x}}g\left(x,r,0\right)\nu \left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right){\Phi }^{*}\left(\text{d}\nu \right)\\ ={\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}x}}g\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right).\end{array}$ (24)

另一方面，

$\begin{array}{c}{\mathbb{E}}_{u,\upsilon ,\pi }\frac{\ln P\left(t\right)}{t}={\mathbb{E}}_{x,r}\frac{\ln \upsilon }{t}-c_2-e_1{\sigma }_1\gamma +\frac{1}{t}{\mathbb{E}}_{x,r}({\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s\\ +{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s)+{\mathbb{E}}_{x,r}\frac{{\varrho }_2{W}_2\left(t\right)}{t}.\end{array}$

则

$\begin{array}{l}\underset{t\to \infty }{\lim }{\mathbb{E}}_{u,\upsilon ,\pi }\frac{\ln P\left(t\right)}{t}\\ =-c_2-e_1{\sigma }_1\gamma +\underset{t\to \infty }{\lim }{\mathbb{E}}_{x,r}\frac{1}{t}\left({\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}y}}\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{1}x}}g\left(x,N\left(s\right),P\left(s\right)\right){\Pi }_s\left(\text{d}x\right)\text{d}s\right)\\ =-c_2-e_1{\sigma }_1\gamma +{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}y}}\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right)+{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{1}x}}g\left(x,r,0\right){\mu }^{*}\left(\text{d}x\right)\hat{\mu }\left(\text{d}r\right)\\ =\lambda >0.\end{array}$

得出

$\underset{t\to \infty }{\lim }{\mathbb{E}}_{u,\upsilon ,\pi }\frac{\ln P\left(t\right)}{t}\le \underset{t\to \infty }{\lim }{\mathbb{E}}_{u,\upsilon ,\pi }\frac{P\left(t\right)}{t}=0.$

又因为 $\ln P\le P$ ，且引理3.1表明了 ${\lim }_{t\to \infty }{\mathbb{E}}_{u,\upsilon ,\pi }\frac{P\left(t\right)}{t}=0$ ，有矛盾。因此， $\left(N\left(t\right),P\left(t\right),\Pi \left(t\right)\right)$ 的所有不变测度集中在 ${ℝ}_{+}^{2,0}\times {\mathcal{M}}_{{\Phi }^{*}}$ 。

运用引理3.1中的矩有界性，当 $k\to \infty$ 时，得到一个序列 $T_k\to \infty$ 使得

$\begin{array}{l}\underset{t\to \infty }{\lim \inf }\frac{1}{t}{\displaystyle {\int }_0^t{\mathbb{E}}_{u,\upsilon ,\pi }}N\left(s\right)\text{d}s=\underset{t\to \infty }{\lim }\frac{1}{T_k}{\displaystyle {\int }_0^{T_k}{\mathbb{E}}_{u,\upsilon ,\pi }}N\left(s\right)\text{d}s,\\ \underset{t\to \infty }{\lim \inf }\frac{1}{t}{\displaystyle {\int }_0^t{\mathbb{E}}_{u,\upsilon ,\pi }}P\left(s\right)\text{d}s=\underset{t\to \infty }{\lim }\frac{1}{T_k}{\displaystyle {\int }_0^{T_k}{\mathbb{E}}_{u,\upsilon ,\pi }}P\left(s\right)\text{d}s.\end{array}$

定理证明完毕。

参考文献

NOTES

^*通讯作者。