BiCR算法求解Sylvester矩阵方程组的Perhermitian解

The BiCR Algorithm for Solving the Perhermitian Solutions of Sylvester Matrix Equations

摘要: 对于给定的矩阵X∈C^n×n，如果SXS=S^H，其中S是给定的反射矩阵，即S^H=S，S²=I，则称矩阵X为perhermitian矩阵。本文提出一种用于求解Sylvester矩阵方程组的perhermitian解的双共轭残差(BiCR)算法，并且证明了该算法的收敛性。通过选择任意初始perhermitian矩阵，可以在有限步求解出Sylvester矩阵方程组的唯一最小范数perhermitian解。最后，我们给出了一些数值算例来验证该算法的有效性和可行性。

Abstract: For a given matrix X∈C^n×n , matrix X is said to be perhermitian if SXS=S^H , where S is a given re-flection matrix, i.e., S^H=S , S²=I . In this paper, we propose the Bi-Conjugate Residual (BiCR) algorithm for solving the perhermitian solutions of Sylvester matrix equations and prove the con-vergence of the algorithm. By choosing any initial perhermitian matrices, the unique mini-mum-norm perhermitian solutions of the Sylvester matrix equations can be solved in finite steps. Finally, we give some numerical examples to verify the validity and feasibility of the algorithm.

1. 引言

矩阵方程在控制理论 [1] 、系统理论 [2] 和应用数学 [3] 等许多领域都有重要的作用，比如Sylvester矩阵方程可以用来恢复缺失或者损坏的信号或图像 [4] ，也可以用来研究线性时不变系统的稳定性 [5] 。另外，五点差分格式求解椭圆方程时会遇到Sylvester矩阵方程 [6] ，在常微分方程定性理论研究及数值求解的隐式Runge-Kwutta方法与块方法也会涉及到Sylvester矩阵方程 [6] 。对于它的一般解，基于Arnoldi过程，Hu等人 [7] 给出了求解 $AX-XB=C$ 的Galerkin算法和最小残差法(MINRES)；基于块Arnoldi过程，El Guennouni A等人 [8] 给出了求解 $AX-XB=C$ 的块GMRES方法(BGMRES)；为了提高收敛速度和缩短运算时间，基于全局Arnoldi过程，Fatemeh Panjeh Ali Beika等人 [9] 提出了求解Sylvester矩阵方程组的全局完全正交化方法(Gl-FOM)和全局极小残量法(Gl-GMRES)。由于Krylov子空间方法的收敛速度依赖于方程系数矩阵谱的性质，选取合适的预条件矩阵，往往可以提高收敛速度，为了进一步提高算法的收敛速度，Bouhamidi A等人 [10] 给出了预条件块Arnoldi方法求解Sylvester矩阵方程，Kaabi [11] 等人提出了预条件Galerkin算法(PGal)和预条件最小残差法(PMR)求解Sylvester矩阵方程。基于预条件全局Arnoldi过程，徐冬梅等人 [12] 给出了求解Sylvester矩阵方程组的预条件全局正交化方法(PG-FOM)和预条件全局极小残量法(PG-GMRES)。对于约束解，Dehghan和Hajarian [13] [14] 提出了求解广义Sylvester矩阵方程组的自反解和广义双对称解的CGNE方法。Dehghan和Hajarian [15] [16] 也通过推广CGNE方法得到了一般矩阵方程组的解和广义双对称解。但是，一般情况下，CGNE方法收敛速度较慢。最近，吕长青等人 [17] 和Masoud Hajarian [18] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的中心对称解和反中心对称解，证明了这种BiCR算法可以在有限步内找到广义Sylvester矩阵方程组的中心对称解，并且选取特定的初始矩阵，可以得到最小范数解；闫同新等人 [19] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的自反解和反自反解以及最小Frobenius范数对称解；Masoud Hajarian [18] 提出了利用BiCR算法求解广义Sylvester矩阵方程组的对称解，收敛性分析表明，BiCR算法在不存在舍入误差的情况下，可以在有限次迭代内计算出广义Sylvester矩阵方程组的最小Frobenius范数对称解对。然而，Sylvester矩阵方程组的perhermitian解目前还没有被研究过。因此，本文将给出求解Sylvester矩阵方程组的perhermitian解的BiCR算法。

在本文中，考虑如下Sylvester矩阵方程组

${\displaystyle \underset{j=1}{\overset{q}{\sum }}{A}_{ij}{X}_j{B}_{ij}}=C_i,i=1,2,\cdots ,p,$ (1.1)

其中，已知系数矩阵 $A_{ij}\in {ℂ}^{m\times n},B_{ij}\in {ℂ}^{n\times l}$ 和常数矩阵 $C_i\in {ℂ}^{m\times l}$ ， $X_j\in {ℂ}^{n\times n}$ 是未知矩阵。

2. 预备知识

定义2.1 [20] [21] 对给定的反射矩阵 $S\in {ℂ}^{n\times n}$ ，即 $S^H=S$ ， $S^2=I_n$ 。如果矩阵 $X\in {ℂ}^{n\times n}$ 满足条件 $SXS=S^H$ ( $SXS=-S^H$ )，那么称其为反射矩阵S的perhermitian矩阵(skew-perhermitian矩阵)，记为 $X\in \mathbb{P}{ℂ}^{n\times n}$ ( $X\in \mathbb{S}\mathbb{P}{ℂ}^{n\times n}$ )。

定义2.2 [22] [23] 设任意 $X,Y\in {ℂ}^{m\times n}$ ，规定

$\langle X,Y\rangle =\mathrm{Re}\left[tr\left(X^{H}Y\right)\right],$

则称 $\langle X,Y\rangle$ 为矩阵 $X,Y$ 的实内积，记作 $\left({ℂ}^{m\times n},ℝ,\langle \cdot ,\cdot \rangle \right)$ 。

定义2.3 [22] [23] 设矩阵 $X\in {ℂ}^{n\times n}$ ，规定

$\Vert X\Vert =\sqrt{\langle X,X\rangle }=\sqrt{\mathrm{Re}\left[tr\left(X^{H}X\right)\right]},$

则称 $\Vert X\Vert$ 为矩阵X的Frobenius范数，简称F范数。

定义2.4 [22] [23] 设矩阵 $X,Y\in {ℂ}^{n\times n}$ ，如果 $\langle X,Y\rangle =0$ ，那么矩阵 $X,Y$ 是正交的。

引理2.1 设矩阵 $X,Y\in M_n\left(ℂ\right)$ ，有

$\mathrm{Re}\left[tr\left(XY\right)\right]=\mathrm{Re}\left[tr\left(\overline{XY}\right)\right]=\mathrm{Re}\left[tr\left(YX\right)\right]=\mathrm{Re}\left[tr\left(X^{\text{T}}{Y}^{\text{T}}\right)\right]=\mathrm{Re}\left[tr\left(X^H{Y}^H\right)\right].$

引理2.2 设矩阵 $X\in \mathbb{P}{ℂ}^{n\times n},Y\in \mathbb{S}\mathbb{P}{ℂ}^{n\times n}$ ，则矩阵 $X,Y$ 是正交的。

证明：因为

$\begin{array}{c}\langle X,Y\rangle =\mathrm{Re}\left[tr\left(X^{H}Y\right)\right]=-\mathrm{Re}\left[tr\left(SXS\cdot S{Y}^{H}S\right)\right]=-\mathrm{Re}\left[tr\left(X{Y}^H\right)\right]\\ =-\mathrm{Re}\left[tr{\left(X{Y}^H\right)}^H\right]=-\mathrm{Re}\left[tr\left(Y{X}^H\right)\right]=-\mathrm{Re}\left[tr\left(X^{H}Y\right)\right]\\ =-\langle X,Y\rangle ,\end{array}$

所以 $\langle X,Y\rangle =0$ ，因此矩阵 $X,Y$ 正交。 □

引理2.3 设矩阵 $X\in {ℂ}^{n\times n}$ ，那么 $X+S{X}^{H}S\in \mathbb{P}{ℂ}^{n\times n}$ 。

证明：因为

$S\left(X+S{X}^{H}S\right)S=SXS+X^H={\left(X+S{X}^{H}S\right)}^H,$

所以结论成立。 □

根据引理2.3，我们可以很容易地构造一个perhermitian矩阵。

引理2.4 设矩阵 $X\in \mathbb{P}{ℂ}^{n\times n}$ ， $Y\in {ℂ}^{n\times n}$ ， $S\in {ℂ}^{n\times n}$ 为反射矩阵，有

$\frac{1}{2}\mathrm{Re}\left(tr\left(X^H\left(Y+S{Y}^{H}S\right)\right)\right)=\mathrm{Re}\left(tr\left(X^{H}Y\right)\right).$

证明：

$\begin{array}{c}\frac{1}{2}\mathrm{Re}\left(tr\left(X^H\left(Y+S{Y}^{H}S\right)\right)\right)=\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr\left(X^{H}S{Y}^{H}S\right)\right)\right)\\ =\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr\left(S{X}^{H}S{Y}^H\right)\right)\right)\\ =\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr\left(X{Y}^H\right)\right)\right)\\ =\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr{\left(Y{X}^H\right)}^H\right)\right)\end{array}$

$\begin{array}{c}=\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr\left(Y{X}^H\right)\right)\right)\\ =\frac{1}{2}\left(\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)+\mathrm{Re}\left(tr\left(X^{H}Y\right)\right)\right)\\ =\mathrm{Re}\left(tr\left(X^{H}Y\right)\right).\end{array}$

证毕。 □

引理2.5 如果矩阵 $X,Y\in \mathbb{P}{ℂ}^{n\times n}$ ， $\alpha ,\beta \in ℝ$ ，那么 $\alpha X+\beta Y\in \mathbb{P}{ℂ}^{n\times n}$ ，换句话说， $\mathbb{P}{ℂ}^{n\times n}$ 是 ${ℂ}^{n\times n}$ 的一个子空间。

证明：因为

$S\left(\alpha X+\beta Y\right)S=\alpha SXS+\beta SYS=\alpha X^H+\beta Y^H={\left(\alpha X+\beta Y\right)}^H.$

证毕。 □

3. 迭代方法

在这个部分，我们提出一种用于求解Sylvester矩阵方程组的perhermitian解的BiCR算法。

3.1. BiCR算法求解Sylvester矩阵方程组的Perhermitian解(表1)

首先，给出该算法的迭代过程。

Table 1. TheBiCR algorithm for solving the perhermitian solutions of the matrix equations (1.1)

表1. BiCR算法求解矩阵方程组(1.1)的perhermitian解

通过算法3.1，我们可以知道 $X_j\left(k\right),W_j\left(k\right),U_j\left(k\right)$ 和 ${\tilde{U}}_j\left(k\right)$ 都是反射矩阵S的perhermitian矩阵， $X_j\left(k\right)\in \mathbb{P}{ℂ}^{n\times n}$ ， $W_j\left(k\right)\in \mathbb{P}{ℂ}^{n\times n}$ ， $U_j\left(k\right)\in \mathbb{P}{ℂ}^{n\times n}$ ， ${\tilde{U}}_j\left(k\right)\in \mathbb{P}{ℂ}^{n\times n}$ ，其中 $j=1,2,\cdots ,q$ 。

3.2. 收敛性分析

接下来，对该算法进行收敛性分析。我们可以通过以下定理来证明所提算法的收敛性。

定理3.1 如果对于正整数m， $R_i\left(k\right)\ne 0$ 、 $T_i\left(k\right)\ne 0$ ， $k=1,2,\cdots ,m$ ，那么

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(t\right)T_i\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s<t$ (3.1)

${\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(t\right)W_j\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s\ne t$ (3.2)

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(t\right)T_i\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s\ne t$ (3.3)

证明：我们采用数学归纳法来证明这个定理，可以得到上述(3.1)~(3.3)。

首先，当 $s<n<m$ ，我们假设有

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n\right)T_i\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s<t$

${\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s\ne t$

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s\right)\right)\right)}=0,s,t=1,2,\cdots ,m,s\ne t$

根据上述归纳假设，接下来我们来证明 $n+1$ 时(3.1)~(3.3)的情况，可得

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n+1\right)T_i\left(s\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left(R_i\left(n\right)-\alpha \left(n\right)T_i\left(n\right)\right)}^H{T}_i\left(s\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n\right)T_i\left(s\right)\right)\right)}-\alpha \left(n\right){\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s\right)\right)\right)}\\ =0\end{array}$

$\begin{array}{l}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n+1\right)W_j\left(s\right)\right)\right)}\\ ={\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\left(A_{ij}^H{\tilde{V}}_i\left(n+1\right)B_{ij}^H+S{\left(A_{ij}^H{\tilde{V}}_i\left(n+1\right)B_{ij}^H\right)}^{H}S\right)}^H}{W}_j\left(s\right)\right)\right)}\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\left(A_{ij}^H{V}_i\left(n+1\right)B_{ij}^H+S{\left(A_{ij}^H{V}_i\left(n+1\right)B_{ij}^H\right)}^{H}S\right)}^H}{W}_j\left(s\right)\right)\right)}\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(\frac{1}{2}({\displaystyle \underset{i=1}{\overset{p}{\sum }}{B}_{ij}(T_i\left(n\right)-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{\tilde{V}}_i\left(n\right)}}\\ -{\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}{\tilde{V}}_i\left(n-1\right))}^H{A}_{ij}\\ +S(A_{ij}^H(T_i\left(n\right)-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{\tilde{V}}_i\left(n\right)\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}{\tilde{V}}_i\left(n-1\right))B_{ij}^H)S)W_j\left(s\right)))\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(B_{ij}{T}_i^H\left(n\right)A_{ij}+S{A}_{ij}^H{T}_i\left(n\right)B_{ij}^{H}S\right)W_j\left(s\right)}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)}}{\tau \left(n\right)}{W}_j^H\left(n\right)W_j\left(s\right)-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)}}{\tau \left(n-1\right)}{W}_j^H\left(n-1\right)W_j\left(s\right)))\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(T_i^H\left(n\right)A_{ij}{W}_j\left(s\right)B_{ij}+T_i\left(n\right){\left(A_{ij}{W}_j\left(s\right)B_{ij}\right)}^H\right)}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{W}_j^H\left(n\right)W_j\left(s\right)-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}{W}_j^H\left(n-1\right)W_j\left(s\right)))\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr({\displaystyle \underset{i=1}{\overset{p}{\sum }}{T}_i^H\left(n\right)A_{ij}{W}_j\left(s\right)B_{ij}}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{W}_j^H\left(n\right)W_j\left(s\right)}\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}{W}_j^H\left(n-1\right)W_j\left(s\right)))\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}({\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr({\displaystyle \underset{i=1}{\overset{p}{\sum }}{T}_i^H\left(n\right)A_{ij}(U_j\left(s+1\right)+\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(s\right)\right)\right)}}{\sigma \left(s\right)}{\tilde{U}}_j\left(s\right)}}\\ +\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s-1\right)M_i\left(s\right)\right)\right)}}{\sigma \left(s-1\right)}{\tilde{U}}_j\left(s-1\right))B_{ij}))\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}\mathrm{Re}\left(tr\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{W}_j^H\left(n-1\right)W_j\left(s\right)}\right)\right))\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}({\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(s+1\right)\Vert {\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s+1\right)\right)\right)}}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}\\ +\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s\right)M_i\left(s\right)\right)\right)}}{\sigma \left(s\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s\right)\right)\right)}\\ +\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s-1\right)M_i\left(s\right)\right)\right)}}{\sigma \left(s-1\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s-1\right)\right)\right)}\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)}}{\tau \left(n-1\right)}tr\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{W}_j^H\left(n-1\right)W_j\left(s\right)}\right))\end{array}$

$\begin{array}{l}=\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(s+1\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s+1\right)\right)\right)}\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)W_j\left(s\right)\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}\end{array}$ (3.4)

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n+1\right)T_i\left(s\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{A}_{ij}{\tilde{U}}_j\left(n+1\right)B_{ij}}\right)}^H{T}_i\left(s\right)\right)\right)}\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{A}_{ij}{U}_j\left(n+1\right)B_{ij}}\right)}^H{T}_i\left(s\right)\right)\right)}\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr((A_{ij}(W_j\left(n\right)-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n\right)}{\tilde{U}}_j\left(n\right)}\\ -{\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{\tilde{U}}_j\left(n-1\right))B_{ij})}^H{T}_i\left(s\right)))\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr((A_{ij}{W}_j\left(n\right)B_{ij}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n\right)}{T}_i\left(n\right)}\\ -{\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{T}_i\left(n-1\right))}^H{T}_i\left(s\right)))\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{B}_{ij}^H{W}_j^H\left(n\right)A_{ij}^H{T}_i\left(s\right)}\right)\right)}\begin{array}{c}\\ \\ \end{array}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(s\right)\right)\right)}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)})\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}({\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)\left(A_{ij}^H{T}_i\left(s\right)B_{ij}^H\right)\right)\right)}}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma (n-1)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)})\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)\left(A_{ij}^H{T}_i\left(s\right)B_{ij}^H+S{\left(A_{ij}^H{T}_i\left(s\right)B_{ij}^H\right)}^{H}S\right)\right)\right)}}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)})\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(W_j^H\left(n\right)(A_{ij}^H(V_i\left(s+1\right)+\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s\right)M_i\left(s\right)\right)\right)}}{\tau \left(s\right)}{\tilde{V}}_i\left(s\right)}}\\ +\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(s-1\right)N_j\left(s\right)\right)\right)}}{\tau \left(s-1\right)}{\tilde{V}}_i\left(s-1\right))B_{ij}^H+S(A_{ij}^H(V_i\left(s+1\right)+\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s\right)M_i\left(s\right)\right)\right)}}{\tau \left(s\right)}{\tilde{V}}_i\left(s\right)\\ +{\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(s-1\right)N_j\left(s\right)\right)\right)}}{\tau \left(s-1\right)}{\tilde{V}}_i\left(s-1\right))B_{ij}^H)}^{H}S)))\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)})\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}({\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(W_j^H\left(n\right)(W_j\left(s+1\right){\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(s+1\right)\Vert }\begin{array}{c}\\ \stackrel{}{}\\ \end{array}}\\ +\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(s\right)M_i\left(s\right)\right)\right)}}{\tau \left(s\right)}{W}_j\left(s\right)+\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(s-1\right)N_j\left(s\right)\right)\right)}}{\tau \left(s-1\right)}{W}_j\left(s-1\right))))\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n-1\right)}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)})\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(s+1\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(s+1\right)\right)\right)}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(s\right)\right)\right)}}{\sigma \left(n-1\right)}\end{array}$ (3.5)

当 $s=n-1$ ，由于 $s<n$ ，根据上述(3.1)~(3.3)，可得

${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n+1\right)T_i\left(n-1\right)\right)\right)}=0.$

$\begin{array}{l}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n+1\right)W_j\left(n-1\right)\right)\right)}\\ =\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}\\ -\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)W_j\left(n-1\right)\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}\end{array}$

$\begin{array}{l}=\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\\ =\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right){\displaystyle \underset{i=1}{\overset{p}{\sum }}{A}_{ij}^H{T}_i\left(n\right)B_{ij}^H}\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\\ =\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left(A_{ij}{W}_j\left(n-1\right)B_{ij}\right)}^H{T}_i\left(n\right)\right)\right)}}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\end{array}$

$\begin{array}{l}=\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}(tr(({\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }{T}_i\left(n\right)\begin{array}{c}\\ \stackrel{}{}\\ \end{array}}\\ +\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n-1\right)\right)\right)}}{\sigma (n-1)}{T}_i\left(n-1\right)\\ +{\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-2\right)M_i\left(n-1\right)\right)\right)}}{\sigma \left(n-2\right)}{T}_i\left(n-2\right))}^H{T}_i\left(n\right)))\\ =\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n\right)\Vert }}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}\\ =0.\end{array}$

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n+1\right)T_i\left(n-1\right)\right)\right)}\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)T_i\left(n-1\right)\right)\right)}}{\sigma \left(n-1\right)}\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(n\right)\right)\right)}}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)\left({\displaystyle \underset{j=1}{\overset{q}{\sum }}{A}_{ij}{W}_j\left(n\right)B_{ij}}\right)\right)\right)}}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\end{array}$

$\begin{array}{l}=\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\\ -\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(\left(A_{ij}^H{T}_i\left(n-1\right)B_{ij}^H\right)W_j\left(n\right)\right)\right)}}\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\\ -\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\left(A_{ij}^H{T}_i\left(n-1\right)B_{ij}^H+S{\left(A_{ij}^H{T}_i\left(n-1\right)B_{ij}^H\right)}^{H}S\right)}^H{W}_j\left(n\right)}\right)\right)}\\ =\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\\ -\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr(({\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert W_j\left(n\right)}+\frac{\mathrm{Re}{\displaystyle \underset{i=1}{\overset{p}{\sum }}tr\left(T_i^H\left(n-1\right)M_i\left(n-1\right)\right)}}{\tau \left(n-1\right)}{W}_j\left(n-1\right)}\\ +{\frac{\mathrm{Re}{\displaystyle \underset{j=1}{\overset{q}{\sum }}tr\left(W_j^H\left(n-2\right)N_j\left(n-1\right)\right)}}{\tau \left(n-2\right)}{W}_j\left(n-2\right))}^H{W}_j\left(n\right)))\end{array}$

$\begin{array}{l}=\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n\right)\Vert }}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\\ =0.\end{array}$

当 $s=n$ 时，通过归纳假设可得

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n+1\right)T_i\left(n\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left(R_i\left(n\right)-\alpha \left(n\right)T_i\left(n\right)\right)}^H{T}_i\left(n\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)R_i\left(n\right)\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert T_i\left(n\right)\Vert }^2}}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(n\right)T_i\left(n\right)\right)\right)}-{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)R_i\left(n\right)\right)\right)}\\ =0.\end{array}$

$\begin{array}{l}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n+1\right)W_j\left(n\right)\right)\right)}\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}(tr((\frac{1}{2}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{T}_i\left(n\right)B_{ij}^H+S{\left(A_{ij}^H{T}_i\left(n\right)B_{ij}^H\right)}^{H}S\right)}\begin{array}{c}\\ \stackrel{}{}\\ \end{array}}\\ -\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{W}_j\left(n\right)-\frac{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n-1\right)N_j\left(n\right)\right)\right)}}{\tau \left(n-1\right)}{W}_j\left(n-1\right))W_j\left(n\right)))\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\left({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right){\displaystyle \underset{j=1}{\overset{q}{\sum }}{A}_{ij}{W}_j\left(n\right)B_{ij}}\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\tau \left(n\right)}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\right)\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\left({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}{\Vert W_j\left(n\right)\Vert }^2}}{\displaystyle \underset{j=1}{\overset{q}{\sum }}\mathrm{Re}\left(tr\left(W_j^H\left(n\right)W_j\left(n\right)\right)\right)}\right)\\ =\frac{1}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\Vert V_i\left(n+1\right)\Vert }}\left({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}-{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}\right)\\ =0.\end{array}$

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n+1\right)T_i\left(n\right)\right)\right)}\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}(tr(({\displaystyle \underset{j}{\overset{q}{\sum }}{A}_{ij}{W}_j\left(n\right)B_{ij}}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{\sigma \left(n\right)}{T}_i\left(n\right)}\\ -{\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n-1\right)M_i\left(k\right)\right)\right)}}{\sigma \left(n-1\right)}{T}_i\left(n-1\right))}^H{T}_i\left(n\right)))\end{array}$

$\begin{array}{l}=\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\left({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(M_i^H\left(n\right)T_i\left(n\right)\right)\right)}-\frac{{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)M_i\left(n\right)\right)\right)}}{{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert T_i\left(n\right)\Vert }^2}}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(n\right)T_i\left(n\right)\right)\right)}\right)\\ =\frac{1}{{\displaystyle \underset{j=1}{\overset{q}{\sum }}\Vert U_j\left(n+1\right)\Vert }}\left({\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(M_i^H\left(n\right)T_i\left(n\right)\right)\right)}-{\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(M_i^H\left(n\right)T_i\left(n\right)\right)\right)}\right)\\ =0.\end{array}$

因此，对于次数 $n+1$ 成立，数学归纳法证明完成。 □

定理3.2假设矩阵方程组(1.1)是相容的，在没有舍入误差的情况下，对任意初始矩阵 $X_j\left(1\right)\in \mathbb{P}{ℂ}^{n\times n}$ ，根据算法3.1，可以在有限步迭代得到矩阵方程组(1.1)的perhermitian解。

证明 首先，定义空间 ${ℂ}^{m\times l}\times {ℂ}^{m\times l}\times \cdots \times {ℂ}^{m\times l}$ 的实内积为 $\langle T_i,T_j\rangle =\mathrm{Re}\left(tr\left(T_j^H{T}_i\right)\right)$ ，其中 $T_i,T_j\in {ℂ}^{m\times l},i,j=1,2,\cdots ,p$ 。如果 $T_i\left(k\right)\ne 0,k=1,2,\cdots ,pml$ ，那么 $\left\{T_1\left(k\right),T_2\left(k\right),\cdots ,T_p\left(k\right)\right\}$ 是该空间的一组正交基。根据(3.1)式可以得到 $R_i\left(pml+1\right)=0$ ，即 $X_j\left(pml+1\right),j=1,2,\cdots ,q$ 是矩阵方程(1.1)的perhermitian解。

定理3.3 算法3.1中残量范数具有以下性质

${\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k+1\right)\Vert }^2}\le {\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}.$

证明：

$\begin{array}{c}{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k+1\right)\Vert }^2}={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(k+1\right)R_i\left(k+1\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left({\left(R_i\left(k\right)-\alpha \left(k\right)T_i\left(k\right)\right)}^H\left(R_i\left(k\right)-\alpha \left(k\right)T_i\left(k\right)\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(\left(R_i^H\left(k\right)-\alpha \left(k\right)T_i^H\left(k\right)\right)\left(R_i\left(k\right)-\alpha \left(k\right)T_i\left(k\right)\right)\right)\right)}\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(k\right)R_i\left(k\right)\right)\right)}+{\alpha }^2\left(k\right){\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(T_i^H\left(k\right)T_i\left(k\right)\right)\right)}\\ -2\alpha \left(k\right){\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(k\right)T_i\left(k\right)\right)\right)}\end{array}$

$\begin{array}{c}={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}+{\alpha }^2\left(k\right)\sigma \left(k\right)-2{\alpha }^2\left(k\right)\sigma \left(k\right)\\ ={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}-{\alpha }^2\left(k\right)\sigma \left(k\right)\le {\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}.\end{array}$

□

定理3.3表明，如果 ${\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}\ne 0$ 且 ${\displaystyle \underset{i=1}{\overset{p}{\sum }}\mathrm{Re}\left(tr\left(R_i^H\left(k\right)T_i\left(k\right)\right)\right)}\ne 0$ ，那么 ${\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}$ 是严格单调递减的，所以算法3.1是收敛的。

3.3. 最小范数Perhermitian解

接下来考虑Sylvester矩阵方程组(1.1)的最佳逼近perhermitian解，即最小范数perhermitian解。

引理3.1 [19] [24] [25] [26] 设线性矩阵方程 $Ax=b$ 有解 $x^{\ast }\in \mathcal{R}\left(A^{\text{T}}\right)$ ，其中 $\mathcal{R}\left(A^{\text{T}}\right)$ 表示 $A^{\text{T}}$ 的列空间，则 $x^{\ast }$ 是 $Ax=b$ 的唯一最小范数解。

定理3.4 设矩阵方程组(1.1)是相容的，初始值取 $X_j\left(1\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{E}_i{B}_{ij}^H+S{\left(A_{ij}^H{E}_i{B}_{ij}^H\right)}^{H}S\right)}$ ，

$Z_j\left(1\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{F}_i{B}_{ij}^H+S{\left(A_{ij}^H{F}_i{B}_{ij}^H\right)}^{H}S\right)}$ ， $j=1,2,\cdots ,q$ ，其中 $E_i$ 和 $F_i$ 为任意的 ${ℂ}^{m\times l}$ 矩阵，特别地，取

$X_j\left(1\right)=0$ ， $Z_j\left(1\right)=0$ ，S是适当维数的反射矩阵。如果矩阵方程组(1.1)有perhermitian解，那么算法3.1经过有限步迭代求出的解是矩阵方程(1.1)的唯一的最小范数perhermitian解 $X_j^{\ast }$ ， $j=1,2,\cdots ,q$ 。

证明：根据Kronecker积，将 $X_j\left(1\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{E}_i{B}_{ij}^H+S{\left(A_{ij}^H{E}_i{B}_{ij}^H\right)}^{H}S\right)}$ 改写为

$\underset{{\mathcal{X}}^{\ast }\left(1\right)}{\underset{︸}{\left(\begin{array}{c}{\left(vec\left(X_1\left(1\right)\right)\right)}^H\\ ⋮\\ {\left(vec\left(X_q\left(1\right)\right)\right)}^H\end{array}\right)}}=\underset{{\mathcal{A}}^H}{\underset{︸}{\left(\begin{array}{ccccc}{B}_{11}\otimes A_{11}^H& S{A}_{11}^H\otimes S{B}_{11}& \cdots & B_{p1}\otimes A_{p1}^H& S{A}_{p1}^H\otimes S{B}_{p1}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ B_{1q}\otimes A_{1q}^H& S{A}_{1q}^H\otimes S{B}_{1q}& \cdots & B_{pq}\otimes A_{pq}^H& S{A}_{pq}^H\otimes S{B}_{pq}\end{array}\right)}}\underset{\mathcal{M}}{\underset{︸}{\left(\begin{array}{c}{\left(vec\left(E_1\right)\right)}^H\\ {\left(vec\left(E_1^H\right)\right)}^H\\ ⋮\\ {\left(vec\left(E_p\right)\right)}^H\\ {\left(vec\left(E_p^H\right)\right)}^H\end{array}\right)}}$

因此，如果通过上述选择 $X_j\left(1\right)$ ，那么通过算法3.1得到的 $X_j\left(k\right)$ 满足

${\mathcal{X}}^{\ast }\left(k\right)={\left({\left(vec\left(X_1\left(k\right)\right)\right)}^H,\cdots ,{\left(vec\left(X_q\left(k\right)\right)\right)}^H\right)}^H\in \mathcal{R}\left({\mathcal{A}}^H\right)$ ，其中 $\mathcal{R}\left({\mathcal{A}}^H\right)$ 表示 ${\mathcal{A}}^H$ 的列空间。由引理3.1可知，如果 $X_j\left(1\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{E}_i{B}_{ij}^H+S{\left(A_{ij}^H{E}_i{B}_{ij}^H\right)}^{H}S\right)}$ ， $Z_j\left(1\right)={\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(A_{ij}^H{F}_i{B}_{ij}^H+S{\left(A_{ij}^H{F}_i{B}_{ij}^H\right)}^{H}S\right)}$ ，作为初始解，

特别是 $X_j\left(1\right)=0$ ， $Z_j\left(1\right)=0$ ，那么可以通过算法3.1来求解矩阵方程组(1.1)的唯一最小范数perhermitian解。

□

4. 数值算例

在这个部分，我们给出两个算例来说明所提出的算法的有效性。当 $r\left(k\right)=\sqrt{{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\Vert R_i\left(k\right)\Vert }^2}}\le {10}^{-10}$ 时，停止迭代，并且 $X_j\left(k\right)$ 被视为矩阵方程组(1.1)的唯一最小范数perhermitian解。

例4.1 给定Sylvester矩阵方程为

$A_{11}{X}_1{B}_{11}+A_{12}{X}_2{B}_{12}=C_1,$

其中

$A_{11}=\left(\begin{array}{ccc}6+5i& 5+6i& 1+6i\\ 3+7i& 10+4i& 2+i\\ 2+i& 9+10i& 3+2i\\ 3+9i& 4+6i& 6+3i\end{array}\right),B_{11}=\left(\begin{array}{cccc}8+5i& 9+2i& 9+9i& 1+3i\\ 6+3i& 7+i& 2+4i& 6+4i\\ 2+7i& 4+3i& 1+10i& 4+7i\end{array}\right),$

$A_{12}=\left(\begin{array}{ccc}4+3i& 10+2i& 4+i\\ 2+5i& 1+5i& 8+7i\\ 3+7i& 4+i& 2+10i\\ 10+2i& 6+8i& 10+4i\end{array}\right),B_{12}=\left(\begin{array}{cccc}6+2i& 9+4i& 8+3i& 6+4i\\ 10+8i& 9+9i& 5+3i& 8+9i\\ 10+2i& 2+3i& 6+9i& 1+i\end{array}\right),$

$C_1={10}^2\times \left(\begin{array}{cccc}1.3500+2.8400i& 1.6000+2.9600i& 0.1800+2.6500i& 0.3600+2.5500i\\ 0.7200+3.1900i& 0.4100+2.2600i& -0.6400+3.4700i& -0.1700+2.0000i\\ 0.6300+3.2400i& 0.7500+2.5500i& -0.8800+2.7500i& 0.1600+2.4200i\\ 1.2000+4.0300i& 1.1800+3.8500i& 0.1000+4.1700i& 0.1300+3.0800i\end{array}\right),$

求其唯一最小范数perhermitian解。

选取初始矩阵

$X_1\left(1\right)={10}^3\times \left(\begin{array}{ccc}0.5979+0.0000i& 0.9305+0.2703i& 0.2987-0.2502i\\ 0.9305-0.2703i& 1.0413+0.0000i& 0.4424-0.5889i\\ 0.2987+0.2502i& 0.4424+0.5889i& 0.1692+0.0000i\end{array}\right),$

$X_1\left(2\right)={10}^3\times \left(\begin{array}{ccc}0.8504+0.0000i& 0.9667-0.3004i& 0.7801+0.0635i\\ 0.9667+0.3004i& 1.1728+0.0000i& 0.9089+0.4224i\\ 0.7801-0.0635i& 0.9089-0.4224i& 0.5345+0.0000i\end{array}\right),$

根据算法3.1，经过24步迭代终止，得到该矩阵方程的唯一最小范数perhermitian解：

$X_1\left(24\right)={10}^3\times \left(\begin{array}{ccc}1.1948+0.0000i& 1.8609+0.5406i& 0.5974-0.5004i\\ 1.8609-0.5406i& 2.0817+0.0000i& 0.8847-1.1779i\\ 0.5974+0.5004i& 0.8847+1.1779i& 0.3373+0.0000i\end{array}\right),$

$X_2\left(24\right)={10}^3\times \left(\begin{array}{ccc}1.6998+0.0000i& 1.9334-0.6008i& 1.5601+0.1270i\\ 1.9334+0.6008i& 2.3446+0.0000i& 1.8178+0.8648i\\ 1.5601-0.1270i& 1.8178-0.8648i& 1.0680+0.0000i\end{array}\right),$

并且，相应残差的范数 $r=2.4009\times {10}^{-13}<{10}^{-10}$ 。

例4.2 给定Sylvester矩阵方程组为

$\{\begin{array}{l}{A}_{11}{X}_1{B}_{11}+A_{12}{X}_2{B}_{12}=C_1\\ A_{21}{X}_1{B}_{21}+A_{22}{X}_2{B}_{22}=C_2\end{array}$ ，

其中

$A_{11}=\left(\begin{array}{ccc}10+2i& 9+6i& 1+8i\\ 8+4i& 5+4i& 4+i\\ 10+6i& 9+i& 9+7i\\ 6+10i& 6+8i& 5+3i\end{array}\right),B_{11}=\left(\begin{array}{cccc}4+i& 9+8i& 4+6i& 4+3i\\ 6+9i& 6+5i& 7+5i& 6+3i\\ 5+2i& 6+10i& 6+5i& 3+4i\end{array}\right),$

$A_{12}=\left(\begin{array}{ccc}9+9i& 4+3i& 8+9i\\ 3+10i& 4+4i& 8+4i\\ 10+3i& 8+6i& 3+7i\\ 4+5i& 7+4i& 9+7i\end{array}\right),B_{12}=\left(\begin{array}{cccc}5+6i& 5+6i& 5+6i& 10+3i\\ 8+4i& 10+3i& 1+10i& 1+9i\\ 1+2i& 10+2i& 2+6i& 1+3i\end{array}\right),$

$A_{21}=\left(\begin{array}{ccc}2+5i& 9+5i& 2+i\\ 10+8i& 2+i& 7+10i\\ 3+4i& 10+8i& 4+7i\\ 2+9i& 6+5i& 4+9i\end{array}\right),B_{21}=\left(\begin{array}{cccc}3+3i& 5+3i& 10+6i& 5+7i\\ 6+4i& 8+4i& 10+5i& 3+10i\\ 8+9i& 7+2i& 6+10i& 4+4i\end{array}\right),$

$A_{22}=\left(\begin{array}{ccc}5+7i& 4+9i& 4+3i\\ 7+5i& 3+4i& 10+i\\ 2+6i& 4+3i& 2+9i\\ 8+9i& 7+3i& 5+10i\end{array}\right),B_{22}=\left(\begin{array}{cccc}5+5i& 4+4i& 3+7i& 10+2i\\ 4+2i& 5+i& 1+2i& 1+10i\\ 5+9i& 4+10i& 1+9i& 2+i\end{array}\right),$

$C_1={10}^2\times \left(\begin{array}{cccc}0.2800+3.4100i& 1.0800+4.8400i& -0.4600+4.1600i& 0.6200+3.1800i\\ 0.1100+2.4200i& 1.1900+3.7100i& -0.4700+3.1100i& 0.1000+2.7500i\\ 1.7100+3.4200i& 1.8500+5.5200i& 0.2500+4.1600i& 0.9900+2.9800i\\ 0.2200+3.0700i& 0.9400+4.8200i& -0.8600+3.9600i& -0.0700+3.1600i\end{array}\right),$

$C_2={10}^2\times \left(\begin{array}{cccc}0.1300+2.6800i& 0.4800+2.6700i& -0.1400+2.9500i& -0.8900+2.9500i\\ 0.3500+3.8800i& 1.1600+3.4500i& -0.0900+4.5500i& 0.2000+3.1100i\\ -0.8700+3.2400i& -0.1600+2.9700i& -0.9700+3.4000i& -0.9800+3.3600i\\ -1.0200+4.0100i& -0.3100+3.6600i& -1.8800+4.3100i& -0.6600+3.9000i\end{array}\right),$

求其唯一最小范数perhermitian解。

选取初始矩阵

$X_1\left(1\right)={10}^3\times \left(\begin{array}{ccc}2.2322+0.0000i& 2.4950-0.4177i& 1.8794-0.1577i\\ 2.4950+0.4177i& 2.8320+0.0000i& 2.2000+0.1784i\\ 1.8794+0.1577i& 2.2000-0.1784i& 1.5266+0.0000i\end{array}\right),$

$X_2\left(1\right)={10}^3\times \left(\begin{array}{ccc}2.3482+0.0000i& 1.6111-0.3890i& 1.7942-0.0223i\\ 1.6111+0.3890i& 1.2291+0.0000i& 1.2886+0.3338i\\ 1.7942+0.0223i& 1.2886-0.3338i& 1.4593+0.0000i\end{array}\right),$

根据算法3.1，经过19步迭代终止，得到该矩阵方程的唯一最小范数perhermitian解：

$X_1\left(19\right)={10}^3\times \left(\begin{array}{ccc}4.4633+0.0000i& 4.9899-0.8353i& 3.7589-0.3154i\\ 4.9899+0.8353i& 5.6630+0.0000i& 4.4000+0.3567i\\ 3.7589+0.3154i& 4.4000-0.3567i& 3.0522+0.0000i\end{array}\right),$

$X_2\left(19\right)={10}^3\times \left(\begin{array}{ccc}4.6953+0.0000i& 3.2223-0.7781i& 3.5884-0.0445i\\ 3.2223+0.7781i& 2.4572+0.0000i& 2.5773+0.6675i\\ 3.5884+0.0445i& 2.5773-0.6675i& 2.9175+0.0000i\end{array}\right),$

并且，相应残差的范数 $r=4.4335\times {10}^{-12}<{10}^{-10}$ 。

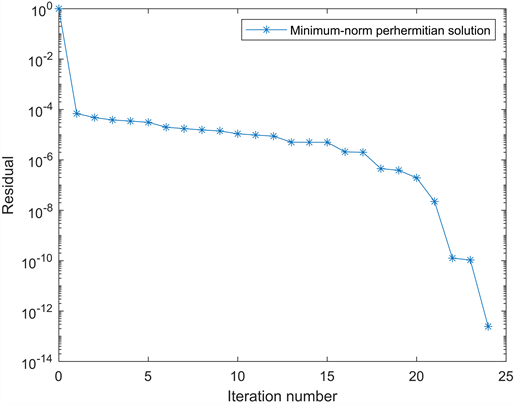
Figure 1. Convergence curves for Example 4.1

图1. 例4.1的收敛曲线

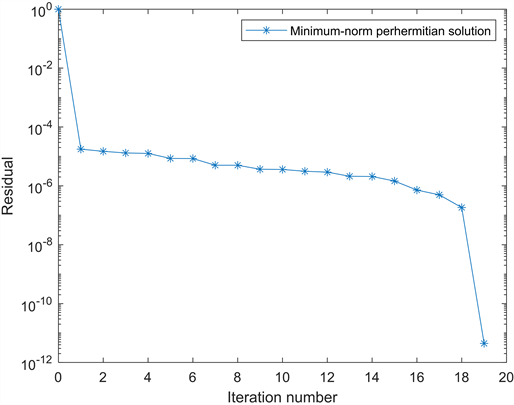
Figure 2. Convergence curves for Example 4.2

图2. 例4.2的收敛曲线

上述两个例子表明，我们的方法能够有效的获得Sylvester矩阵方程组的唯一最小范数perhermitian解。此外，从图1和图2可以看出，算法在数值上是非常可靠的。

5. 总结

在本文中，我们利用BCR算法来求解Sylvester矩阵方程组(1.1)的perhermitian解。我们证明了算法是收敛的，在不存在舍入误差的情况下，可以在有限步内得到唯一的最小范数perhermitian解。最后，通过两个算例说明了算法的可行性和有效性。

NOTES

^*通讯作者。