混合多核极化码指数的收敛性

doi:10.12677/AAM.2024.131006

期刊菜单

混合多核极化码指数的收敛性
Convergence of Hybrid Multi-Kernel Polar Codes Exponent

DOI: 10.12677/AAM.2024.131006, PDF, HTML, XML, 下载: 68 浏览: 109
作者: 王彤, 金小雨, 杨卫华^*：太原理工大学数学学院，山西太原
关键词: 混合多核极化码；指数；收敛性；Hybrid Multi-Kernel Polar Codes； Exponent； Convergence

摘要: 混合多核极化码存在极化现象且有良好的极化性能。极化码对应的极化矩阵的指数是度量极化码性能的重要指标，因此本文主要研究混合多核极化码的指数。本文将多核极化码部分距离的表达式进行拓展，得到混合多核极化码部分距离，根据极化码部分距离和指数的关系推导出了混合多核极化码指数的表达式，即混合多核极化码指数可以表示为其组成矩阵的线性组合，并得到了混合多核极化码指数的上下界；然后基于混合多核极化码的极化现象，提出了一种特殊的混合多核极化码的矩阵选择规则，证明了在这种矩阵选择规则下产生的混合多核极化码的指数是收敛且与信道容量相关；最后应用本文得出的定理，对一些已有的实验图像和猜想进行了解释。

Abstract: Hybrid multi-kernel polar codes are polarized and have good polarization performance. The expo-nent of the polarization matrix corresponding to the polar code is an important metric to measure the performance of the polar codes, so this paper focuses on the exponent of the hybrid multi-kernel polar codes. In this paper, we extend the expression of partial distance of multi-kernel polar codes to obtain the expression of partial distance of hybrid multi-kernel polar codes, and the expression of exponent of hybrid multi-kernel polar codes is derived based on the relationship between partial distance and exponent of polar codes, which can be expressed as a linear combination of its constit-uent matrices, and the upper and lower bounds of exponent of hybrid multi-kernel polar code are obtained. Then, based on the polarization phenomenon of hybrid multi-kernel polar codes, a special matrix selection rule for hybrid multi-kernel polar codes is proposed, and it is proved that the ex-ponent of hybrid multi-kernel polar codes generated under this matrix selection rule is convergent and channel capacity dependent. Finally the theorems derived in this paper are applied to explain some existing experimental images and conjectures.

文章引用：王彤, 金小雨, 杨卫华. 混合多核极化码指数的收敛性[J]. 应用数学进展, 2024, 13(1): 47-54. https://doi.org/10.12677/AAM.2024.131006

1. 引言

ARIKAN教授提出的传统极化码是首个理论上被证明能够实现信道容量的信道编码 [1] 。传统极化码的码长为 $N = 2^{n}$ ，生成矩阵是 $G = F^{\otimes n}$ ( $F$ 为极化变换的核)，其中 $F = [\begin{matrix} 1 & 0 \\ 1 & 1 \end{matrix}]$ ， $\otimes$ 表示克罗内克积。ARIKAN教授还提出信道极化现象是一种普遍存在的现象，即对于 $l \times l$ $(l \geq 2)$ 的核 $G_{l}$ 也会产生信道极化现象 [2] 。为了提升传统极化码码长的灵活性，许多文章提出了不同码长的极化码构造，如线性与非线性二进制的核 [3] ，极化码的多核构造 [4] ，打孔极化码 [5] [6] 以及缩短极化码 [7] 等。

将传统极化码生成矩阵中的 $F$ 替换为 $l_{i} \times l_{i}$ 极化矩阵 $G_{l_{i}}$ 就得到了码长为 $l_{1} l_{2} \dots l_{n}$ 多核极化码，其生成矩阵为 $G = G_{l_{1}} \otimes G_{l_{2}} \otimes \dots \otimes G_{l_{n}}$ 。多核极化码除了适用于不同的码长外，在错误率性能方面还优于使用打孔和缩短过程得到的极化码 [4] 。为了进一步提高极化性，混合多核极化码 [8] 在多核极化码的基础上，根据不同的虚拟信道的性能选择不同的组成矩阵。因此，混合多核极化码是局部最优的，有更好的性能。

同时，信道极化率 [9] 是在SC译码下极化码的一个度量块错误率的重要指标。极化码的极化率也被叫做对应极化矩阵的指数，根据极化码指数的计算公式得到传统极化码的指数为 $E (F^{\otimes n}) = 0.5$ ，多核极化码的指数为 $E (G_{l_{1}} \otimes G_{l_{2}} \otimes \dots \otimes G_{l_{n}}) = \sum_{i = 1}^{n} \frac{E (G_{l_{i}})}{\log_{l_{i}} l_{1} l_{2} \dots l_{n}}$ [10] 。

本文我们的目标是得到混合多核极化码指数的表达式，以推导出某些混合多核极化码指数的收敛性，并将这些理论应用于已有的实验中。

2. 基础知识

2.1. 混合多核极化码

为了提高多核极化码的错误性能，混合多核极化码根据虚拟信道的不同性能在极化的每一阶段选择不同的生成矩阵。如图1所示，我们在混合多核极化码的每一极化阶段根据信道容量选择极化矩阵。

令 $G$ 是一个 $l \times l$ 的极化矩阵， $G_{i} (i = 1, 2, \dots, l)$ 是 $l_{i} \times l_{i}$ 的极化矩阵， $G_{H}$ 是一个混合矩阵，即

$G = [\begin{matrix} α_{1} \\ α_{2} \\ : \\ α_{l} \end{matrix}] = [\begin{matrix} a_{1, 1} & a_{1, 2} & \dots & a_{1, l} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, l} \\ ⋮ & ⋮ & ⋮ \\ a_{l, 1} & a_{l, 2} & \dots & a_{l, l} \end{matrix}], G_{i} = [\begin{matrix} a_{1, 1} & a_{1, 2} & \dots & a_{1, l_{i}} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, l_{i}} \\ ⋮ & ⋮ & ⋮ \\ a_{l_{i}, 1} & a_{l_{i}, 2} & \dots & a_{l_{i}, l_{i}} \end{matrix}], G_{H} = [\begin{matrix} G_{1} \\ G_{2} \\ : \\ G_{l} \end{matrix}]$ . (1)

则矩阵 $G$ 和 $G_{H}$ 的类克罗内克积 [11] 定义如下：

$G ⊠ G_{H} = [\begin{matrix} α_{1} \otimes G_{1} \\ α_{2} \otimes G_{2} \\ : \\ α_{l} \otimes G_{l} \end{matrix}]$ . (2)

混合多核极化码的生成矩阵 [11] 为 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 。

Figure 1. Hybrid multi-kernel polar codes construction

图1. 混合多核极化码的构造

2.2. 指数

将极化现象应用于混合多核极化码，得到如下引理。

引理1 (混合多核极化码的极化性 [12] )：令W是任意二进制输入离散无记忆信道(B-DMC)，信道容量 $0 < I (W) < 1$ ，混合多核极化码的生成矩阵为 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 。当混合多核极化码的码长N趋于无穷时，信道容量趋于1虚拟信道占所有虚拟信道的比例为 $I (W)$ ；信道容量趋于0的虚拟信道占所有虚拟信道的比例为 $1 - I (W)$ 。

定义1 (指数 [2] )：令W是任意二进制输入离散无记忆信道(B-DMC)，信道容量 $0 < I (W) < 1$ ， $l \times l$ 矩阵 $G$ 的指数 $E (G)$ 满足以下条件：

1) 对于任意一个定值 $β < E (G)$ ， $\underset{n \to \infty}{\lim \inf} P r [Z_{n} \leq 2^{- l^{n β}}] = I (W)$ ，

2) 对于任意一个定值 $β > E (G)$ ， $\underset{n \to \infty}{\lim \inf} P r [Z_{n} \geq 2^{- l^{n β}}] = 1$ 。

指数 $E (G)$ 也叫做极化率，是一种在SC译码下测量极化码的块错误率的一种方式。指数 $E ( G )$

由的部分距离计算得到。

定义2 (部分距离 [2] )：令 $G = {[g_{1}^{T}, \dots, g_{l}^{T}]}^{T}$ 为 $l \times l$ 极化矩阵， $G$ 的部分距离为

$D_{G} = {D_{G} (1), D_{G} (2), \dots, D_{G} (l)}$ ，

$D_{G} (i) = d_{H} (g_{i}, 〈 g_{i + 1}, g_{i + 2}, \dots, g_{l} 〉), i = 1, 2, \dots, l - 1$ ， (3)

$D_{G} (l) = d_{H} (g_{l}, 0)$ ， (4)

其中 $〈 g_{i + 1}, g_{i + 2}, \dots, g_{l} 〉 = s p a n {g_{i + 1}, g_{i + 2}, \dots, g_{l}}$ ， $g_{i}^{T}$ 是行向量 $g_{i}$ 的转置， $d_{H} (a, b)$ 是向量 $a$ 和向量 $b$ 的汉明距离， $d_{H} (a, C) = \min_{c \in C} d_{H} (a, c)$ ， $0$ 是 $1 \times l$ 的零向量。

引理2 (部分距离与指数的关系 [2] )：令 $G$ 是一个 $l \times l$ 极化矩阵且 $G$ 的部分距离为

$D_{G} = {D_{G} (1), D_{G} (2), \dots, D_{G} (l)}$ ，则 $G$ 的指数

$E (G) = \frac{1}{l} \sum_{i = 1}^{l} \log_{l} D_{G} (i)$ (5)

3. 主要结论

这部分展示了本文的主要结论，即在一种特殊的选择方式下混合多核极化码的指数是收敛的。

3.1. 混合多核极化码指数的表达式

根据引理2，我们可以通过部分距离与指数的关系计算指数。因此，为了得到混合多核极化码的指数的表达式我们先写出混合多核极化码的部分距离。

引理3 (类克罗内克积的部分距离 [2] )：令 $D_{G} = {D_{G} (1), D_{G} (2), \dots, D_{G} (l)}$ 是极化矩阵 $G$ 的部分距离， $G_{H}$ 是由 $l_{i} \times l_{i}$ 的极化矩阵 $G_{i} (i = 1, 2, \dots, l)$ 组成的混合矩阵， $D_{G_{H}}$ 是 $G_{H}$ 部分距离序列，即 $D_{G_{H}} = {D_{G_{1}}, D_{G_{2}}, \dots, D_{G_{l}}}$ 。则混合多核极化码生成矩阵 $G ⊠ G_{H}$ 的部分距离

$D (G ⊠ G_{H}) = {D_{G} (1) D_{G_{1}}, D_{G} (2) D_{G_{2}}, \dots, D_{G} (l) D_{G_{l}}}$ . (6)

定理1：令 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 为混合多核极化码的生成矩阵， $G_{j}^{(i)}$ 是极化过程中第i阶段的第j个矩阵，则

$E (G_{n}) = \sum_{i = 1}^{n} \frac{E (G^{(i)})}{\log_{l_{i}} l_{1} l_{2} \dots l_{n}}$ ， (7)

其中 $E (G^{(i)}) = \frac{1}{l_{1} l_{2} \dots l_{i - 1}} \sum_{j = 1}^{l_{1} l_{2} \dots l_{i - 1}} E (G_{j}^{(i)})$ ， $(i = 2, \dots, n)$ ，即混合多核极化码极化过程中第i阶段的所有组成矩阵指数的平均值。

证明：该定理的证明主要运用了数学归纳法。

1) 当 $n = 2$ 时，

$D_{G_{H}^{(2)}} = {D_{G_{1}^{(2)}}, D_{G_{2}^{(2)}}, \dots, D_{G_{l_{1}}^{(2)}}}$ ， (8)

$D_{G^{(1)}} = {D_{G^{(1)}} (1), D_{G^{(1)}} (2), \dots, D_{G^{(1)}} (l_{1})}$ . (9)

根据引理3，

$D_{G_{2}} = D_{G^{(1)}} ⊠ G_{H}^{(2)} = {D_{G^{(1)}} (1) D_{G_{1}^{(2)}}, \dots, D_{G^{(1)}} (l_{1}) D_{G_{l_{1}}^{(2)}}}$ ， (10)

令 $i \div l_{1} = x \dots r$ ，则 $D_{G_{2}} (i)$ 是 $D_{G^{(1)}} (x + 1) D_{G_{x + 1}^{(2)}}$ 的第r项，

$D_{G_{2}} (i) = D_{G^{(1)}} (x + 1) D_{G_{x + 1}^{(2)}} (r)$ ， (11)

因为

$E (G^{(1)}) = \frac{1}{l_{1}} \sum_{i = 1}^{l_{1}} \log_{l_{1}} D_{G^{(1)}} (i)$ ， (12)

$E (G_{j}^{(2)}) = \frac{1}{l_{2}} \sum_{i = 1}^{l_{2}} \log_{l_{2}} D_{G_{j}^{(2)}} (i) (1 \leq j \leq l_{2})$ ， (13)

则

$\begin{matrix} E (G_{2}) = \frac{1}{l_{1} l_{2}} \sum_{i = 1}^{l_{1} l_{2}} \log_{l_{1} l_{2}} D_{G_{2}} (i) \\ = \frac{1}{l_{1} l_{2}} \sum_{i = 1}^{l_{1} l_{2}} \log_{l_{1} l_{2}} D_{G^{(1)}} (x + 1) D_{G_{x + 1}^{(2)}} (r) \\ = \frac{1}{l_{1} l_{2}} \sum_{i = 1}^{l_{1} l_{2}} [\log_{l_{1} l_{2}} D_{G^{(1)}} (x + 1) + \log_{l_{1} l_{2}} D_{G_{x + 1}^{(2)}} (r)] \\ = \frac{E (G^{(1)})}{\log_{l_{1}} l_{1} l_{2}} + \frac{\frac{1}{l_{1}} \sum_{j = 1}^{l_{1}} E (G_{j}^{(2)})}{\log_{l_{2}} l_{1} l_{2}} \\ = \frac{E (G^{(1)})}{\log_{l_{1}} l_{1} l_{2}} + \frac{E (G^{(2)})}{\log_{l_{2}} l_{1} l_{2}} \end{matrix}$ (14)

2) 假设结论对于 $n - 1$ 成立，即

$E (G_{n - 1}) = \sum_{i = 1}^{n - 1} \frac{E (G^{(i)})}{\log_{l_{i}} l_{1} l_{2} \dots l_{n - 1}}$ . (15)

3) 当 $k = n$ 时，则

$E (G_{n}) = E (G_{n - 1} ⊠ G_{H}^{(n)}) = \frac{E (G_{n - 1})}{\log_{l_{1} l_{2} \dots l_{n - 1}} l_{1} l_{2} \dots l_{n}} + \frac{\frac{1}{l_{1} l_{2} \dots l_{n - 1}} \sum_{j = 1}^{l_{1} l_{2} \dots l_{n}} E (G_{j}^{(n)})}{\log_{l_{n}} l_{1} l_{2} \dots l_{n}}$ . (16)

将(16)式带入(15)式并化简，我们得到

$E (G_{n}) = \frac{E (G^{(1)})}{\log_{l_{1}} l_{1} l_{2} \dots l_{n}} + \frac{E (G^{(2)})}{\log_{l_{2}} l_{1} l_{2} \dots l_{n}} + \dots + \frac{E (G^{(n)})}{\log_{l_{n}} l_{1} l_{2} \dots l_{n}} = \sum_{i = 1}^{n} \frac{E (G^{(i)})}{\log_{l_{i}} l_{1} l_{2} \dots l_{n}}$ . (17)

注：若在混合多核极化码极化过程的第 $i (i = 2, \dots, n)$ 阶段选择相同的组成矩阵，就得到了多核极化码指数的表达式，这与文献 [10] 中得到的结果相同。

若给出了组成矩阵中的指数最大和指数最小的矩阵，根据以下推论我们可以得到混合多核极化码的指数 $E (G_{n})$ 介于其组成矩阵的最大指数和最小指数之间。

推论1：令 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 是混合多核极化码的生成矩阵，若 $G_{L}$ 为混合多核极化码组成矩阵中指数最大的矩阵， $G_{S}$ 为混合多核极化码组成矩阵中指数最小的矩阵，则

$E (G_{S}) \leq E (G_{n}) \leq E (G_{L})$ . (18)

证明：首先证明右边的不等式。

根据(7)式，

$\begin{matrix} E (G_{n}) = \frac{E (G^{(1)})}{\log_{l_{1}} l_{1} l_{2} \dots l_{n}} + \frac{E (G^{(2)})}{\log_{l_{2}} l_{1} l_{2} \dots l_{n}} + \dots + \frac{E (G^{(n)})}{\log_{l_{n}} l_{1} l_{2} \dots l_{n}} \\ \leq \frac{E (G_{L})}{\log_{l_{1}} l_{1} l_{2} \dots l_{n}} + \frac{E (G_{L})}{\log_{l_{2}} l_{1} l_{2} \dots l_{n}} + \dots + \frac{E (G_{L})}{\log_{l_{n}} l_{1} l_{2} \dots l_{n}} \\ = E (G_{L}) [\frac{1}{\log_{l_{1}} l_{1} l_{2} \dots l_{n}} + \frac{1}{\log_{l_{2}} l_{1} l_{2} \dots l_{n}} + \dots + \frac{1}{\log_{l_{n}} l_{1} l_{2} \dots l_{n}}] \\ = E (G_{L}) [\log_{l_{1} l_{2} \dots l_{n}} l_{1} + \log_{l_{1} l_{2} \dots l_{n}} l_{2} + \dots + \log_{l_{1} l_{2} \dots l_{n}} l_{n}] \\ = E (G_{L}) \end{matrix}$ (19)

重复以上步骤，就得到了左边的不等式，此处不再赘述。

根据引理1，当混合多核极化码的码长趋于无穷时，虚拟信道中信道容量接近1的虚拟信道占所有虚拟信道的比例为 $I (W)$ ，信道容量接近0的虚拟信道占所有信道的比例为 $1 - I (W)$ 。根据这个特点，我们提出一种矩阵选择规则：信道容量接近1的虚拟信道选择极化矩阵 $G_{x}$ ，信道容量接近0的虚拟信道选择极化矩阵 $G_{y}$ ，剩余的虚拟信道可以选择任意极化矩阵。接下来我们证明在这种选择规则下生成的混合多核极化码的指数是收敛的且与信道容量相关。

3.2. 混合多核极化码指数的收敛性

定理2：令 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 是混合多核极化码的生成矩阵，W (B-DMC)为二进制输入离散无记忆信道，信道容量 $0 < I (W) < 1$ 。当 $n \to \infty$ 时，若根据以上规则选择组成矩阵，则

$\lim_{n \to \infty} E (G_{n}) = I (W) E (G_{x}) + (1 - I (W)) E (G_{y})$ . (20)

证明：令k为一个固定的足够的大的正整数，根据以上矩阵选择规则，在第k阶段，有 $(l_{1} l_{2} \dots l_{k}) I (W)$ 个虚拟信道选择极化矩阵 $G_{x}$ ；有 $(l_{1} l_{2} \dots l_{k}) (1 - I (W))$ 个虚拟信道选择极化矩阵 $G_{y}$ 。由定理1中 $E (G^{(k)})$ 的定义， $\lim_{k \to \infty} E (G^{(k)}) = I (W) E (G_{x}) + (1 - I (W)) E (G_{y})$ 。

我们将等式(7)分成两部分，第一部分是等式的前k项；第二部分是等式的 $k + 1$ 项及其后所有项，根据上一段分析，等式第二部分中的每一项都接近于 $I (W) E (G_{x}) + (1 - I (W)) E (G_{y})$ 。当n不断增加时，由于k是固定值且第一部分的 $E (G^{(i)})$ 的系数不断减少，则第一部分 $E (G^{(i)})$ 的系数和递减。根据(7)式，可以明显看出等式中所有 $E (G^{(i)})$ 的系数和为1，当 $n \to \infty$ 时，第一部分的系数和趋近于0，那么第二部分 $E (G^{(i)})$ 的系数和趋近1。因此，第一部分的和趋近于0，第二部分和趋近于 $I (W) E (G_{x}) + (1 - I (W)) E (G_{y})$ 。因此 $\lim_{n \to \infty} E (G_{n}) = I (W) E (G_{x}) + (1 - I (W)) E (G_{y})$ 。

推论2：令W是二进制擦除信道(BEC)且 $ϵ$ 为其擦除概率，混合多核极化码的生成矩阵为 $G_{n} = G^{(1)} ⊠ G_{H}^{(2)} ⊠ G_{H}^{(3)} ⊠ \dots ⊠ G_{H}^{(n)}$ 。当 $n \to \infty$ 时，如果根据以上规则选择组成矩阵，

$\lim_{n \to \infty} E (G_{n}) = (1 - ϵ) E (G_{x}) + ϵ E (G_{y})$ . (21)

证明：对于任意的二进制擦除信道(BEC) W有 $I (W) = 1 - ϵ$ ，显然等式(21)成立。

4. 数值分析

最后，我们给出码长为 $N = 3^{n}$ 的混合多核极化码的例子。

令 $G$ 是一个 $N \times N$ 极化矩阵，W是二进制擦除信道(BEC)且信道容量为 $ϵ$ ， $W_{N}^{(i)} (1 \leq i \leq N)$ 是由 $G$ 生成的第i个虚拟信道， $Z (W_{N}^{(i)})$ 是 $W_{N}^{(i)}$ 的巴氏参数。我们用文献 [11] 中的构造方法。

令

$G_{3 x} = [\begin{matrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{matrix}], G_{3 y} = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \end{matrix}]$ ， (22)

则码长为 $N = 3^{n}$ 的混合多核极化码的生成矩阵为

$G_{n} = G_{3 H}^{(1)} ⊠ G_{3 H}^{(2)} ⊠ G_{3 H}^{(3)} ⊠ \dots ⊠ G_{3 H}^{(n)}$ ， (23)

其中

$G_{3 H}^{(i)} = [\begin{matrix} G_{1}^{(i)} \\ G_{2}^{(i)} \\ : \\ G_{3^{i - 1}}^{(i)} \end{matrix}], 1 \leq i \leq n$ 对于 $1 \leq j \leq 3^{i - 1}$ ， (24)

根据虚拟信道的信道容量 $ϵ^{'}$ ， $G_{j}^{(i)}$ 取 $G_{3 x}$ 或 $G_{3 y}$ ：当 $ϵ^{'} \in (0, 0.5)$ ，取 $G_{3 x}$ ；当 $ϵ^{'} \in (0.5, 1)$ ，取 $G_{3 y}$ ；当 $ϵ^{'} = 0.5$ ，取 $G_{3 x}$ 或 $G_{3 y}$ 。

通过计算， $E (G_{3 x}) \approx 0.42062$ ， $E (G_{3 y}) \approx 0.33333$ 根据推论2和(23)式，混合多核极化码的指数收敛为

$\lim_{n \to \infty} E (G_{n}) = (1 - ϵ) E (G_{3 x}) + ϵ E (G_{3 y})$ . (25)

当 $ϵ = 0.5$ ，指数收敛为 $\frac{1}{2} (E (G_{3 x}) + E (G_{3 y}))$ 。

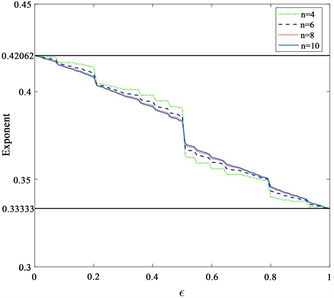
Figure 2. Exponents of hybrid multi-kernels polar codes

图2. 混合多核极化码的指数

图2为文献 [11] 中模拟码长为 $N = 3^{n} (n = 4, 6, 8, 10)$ 时混合多核极化码的指数图像。在图中我们可以观察到，指数会在某些 $ϵ$ 值处出现突变。产生这些突变有两个原因：一是当初始信道的擦除概率为0.5时，在第一阶段无法确定对应的组成矩阵；二是在极化过程中的其他阶段出现的擦除概率为0.5的虚拟信道时无法确定对应的组成矩阵。

当 $n \to \infty$ 时，这些突变会消失。由于信道极化，当n足够大时，擦除概率为0.5的虚拟信道非常少。因此不管这些信道取 $G_{3 x}$ 或者 $G_{3 y}$ ，对于 $E (G_{n})$ 的取值几乎没有影响，即 $\lim_{n \to \infty} E (G_{n}) = (1 - ϵ) E (G_{3 x}) + ϵ E (G_{3 y})$ 。根据(25)式，在图2中，当 $n \to \infty$ 时，混合多核极化码的指数应该为一条过点 $(0, 0.42062)$ 和 $(1, 0.33333)$ 的直线。

5. 总结

极化码的指数是度量极化码性能的重要指标，为了探究混合多核极化码的指数的相关性质，本文得到了混合多核极化码指数的表达式，即混合多核极化码指数可以表示为其组成矩阵的线性组合并且提出了一种特殊的矩阵选择规则，证明了在这种选择规则下混合多核极化码的指数是收敛的。文献 [11] 对混合多核极化码的指数进行了仿真，得到了一类混合多核极化码指数的图像，并针对图像提出了一些猜想。本文将推导出的定理运用到文献 [11] 的实验中，解释了图像产生突变的原因，预测了当极化码码长趋于无穷时的图像走向，证实了其猜想。

NOTES

^*通讯作者。

参考文献

[1]	Arikan, E. (2009) Channel Polarization: A Method for Constructing Capacity Achieving Codes for Symmetric Bina-ry-Input Memoryless Channels. IEEE Transactions on Information Theory, 55, 3051-3073. https://doi.org/10.1109/TIT.2009.2021379
[2]	Korada, S.B., Sasoglu, E. and Urbanke, R. (2010) Polar Codes: Characterization of Exponent, Bounds, and Constructions. IEEE Transactions on Information Theory, 56, 6253-6264. https://doi.org/10.1109/TIT.2010.2080990
[3]	Lin, H.P., Lin, S. and Abdel-Ghaffar, K.A.S. (2015) Linear and Nonlinear Binary Kernels of Polar Codes of Small Dimensions with Maximum Exponents. IEEE Transactions on In-formation Theory, 61, 5253-5270. https://doi.org/10.1109/TIT.2015.2469298
[4]	Gabry, F., Bioglio, V., Land, I., et al. (2017) Multi-Kernel Con-struction of Polar Codes. 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, 21-25 May 2017, 761-765. https://doi.org/10.1109/ICCW.2017.7962750
[5]	Niu, K., Chen, K. and Lin, J.R. (2013) Beyond Turbo Codes: Rate-compatible Punctured Polar Codes. 2013 IEEE International Conference on Communications (ICC), Budapest, 9-13 June 2013, 3423-3427. https://doi.org/10.1109/ICC.2013.6655078
[6]	Zhang, L., Zhang, Z.Y., Wang, X.B., et al. (2014) On the Punc-turing Patterns for Punctured Polar Codes. 2014 IEEE International Symposium on Information Theory (ISIT), Hawaii, 29 June-4 July 2014, 121-125. https://doi.org/10.1109/ISIT.2014.6874807
[7]	Wang, R.X. and Liu R.K. (2014) A Novel Puncturing Scheme for Polar Codes. IEEE Communications Letters, 18, 2081-2084. https://doi.org/10.1109/LCOMM.2014.2364845
[8]	Cheng, L., Zhou, W. and Zhang, L.J. (2019) Hybrid Mul-ti-Kernel Construction of Polar Codes. 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, 28 April-1 May 2019, 1-5. https://doi.org/10.1109/VTCSpring.2019.8746303
[9]	Arikan, E. and Telatar, E. (2009) On the Rate of Channel Polarization. 2009 IEEE International Symposium on Information Theory, Seoul, 28 June-3 July 2009, 1493-1495. https://doi.org/10.1109/ISIT.2009.5205856
[10]	Lee, M.-K. and Yang, K. (2014) The Exponent of a Polarizing Matrix Constructed from The Kronecker Product. Designs Codes Cryptography, 70, 313-322. https://doi.org/10.1007/s10623-012-9689-z
[11]	Cheng, L., Zhang, L.J. and Sun, Q. (2018) Exponents of Hybrid Multi-Kernel Polar Codes. 2018 IEEE 10th International Symposium on Turbo Codes & Iterative Information Pro-cessing (ISTC), Hong Kong, 3-7 December 2018, 1-5. https://doi.org/10.1109/ISTC.2018.8625322
[12]	宋睿, 徐铭, 唐元生. 混合多核极化码的极化性极化性[J]. 广西师范大学学报(自然科学版), 2021, 39(3): 69-82.

为你推荐

友情链接