基于非光滑约束的Langevin算法

Langevin Algorithms Based on Non-Smooth Constraints

摘要: 贝叶斯推断求解反问题越来越流行，得益于它对解不确定性的诠释。在解决实际问题中，算法的计算时间受到一定的关注，而基于Langevin方程的算法利用了一阶导数信息，具有采样效率高的优点，在采样算法中被广泛使用。对于含有急剧跳跃先验信息的图像问题，贝叶斯框架下先验的选取尤为重要，而TV正则化方法等非光滑约束可以很好刻画先验信息。本文回顾了非光滑约束与高斯先验相结合的混合先验，同时重述了近端Langevin算法，并在此基础上提出了基于非光滑约束的对偶Langevin算法。最后应用于CT成像问题，数值结果表明，我们提出算法是有效的，能够更好地利用非光滑约束刻画解。

Abstract: Bayesian inference for solving inverse problems is becoming increasingly popular, thanks to its in-terpretation of solution uncertainty. In solving practical problems, the computational time of algo-rithms has received certain attention, and algorithms based on Langevin equation utilize first-order derivative information, which has the advantage of high sampling efficiency and is widely used in sampling algorithms. For image problems with sharp jump prior information, the selection of prior information in the Bayesian framework is particularly important, and non-smooth constraints such as TV regularization methods can effectively characterize prior information. This article reviews the hybrid prior combining non-smooth constraints with Gaussian prior, while reiterating the proximal Langevin algorithm, and proposes a dual Langevin algorithm based on non-smooth constraints. Fi-nally, it is applied to the CT imaging problem, and numerical results show that our proposed algo-rithm is effective and can better utilize non-smooth constraints to characterize the solution.

1. 引言

本文考虑求解不适定问题

$Au=y$ ，

其中 $A:X\to Y$ 是Hilbert空间X到Hilbert空间Y的有界线性算子。在实际应用中，真实数据很难获得，而常常只能得到带有噪声的扰动数据 $y=y^{†}+\epsilon$ ， $\epsilon$ 是服从正态分布 $N\left(0,\Sigma \right)$ 的噪声， $\Sigma$ 是对称正定算子。我们关注的问题的不适定性是指解不连续依赖于右端数据。正则化方法是求解不适定问题的基本策略，其利用具体问题的某些附加信息，引进约束泛函给出一个逼近原问题的稳定的近似解 [1] [2] 。当解为不均匀介质，包含不连续点、脉冲尖点等结构时，经典的正则化方法因过光滑而不再适用，一些非光滑约束如全变差约束(TV正则化)、稀疏约束被引入 [3] 。

对一般凸约束 $R:X\to \left(-\infty ,\infty \right]$ 构造约束泛函

$u=\underset{u}{\arg \min }\left\{\frac{1}{2}{\Vert Au-y\Vert }^2+aR\left(u\right)\right\}$ ，

传统的优化方法只能给出反问题的“点估计”，当物理模型或测量数据存在随机性时，我们希望获得更多的统计信息。相应统计反演(贝叶斯推断)结合后验概率分布因其能提供更多重构解的统计信息而得到广泛关注。

在贝叶斯视角下，统计反演问题中对反演解的高斯先验、TV先验、Besov先验与Tikhonov型正则化方法的平方约束、TV约束、稀疏约束相呼应 [4] ，反演解作为随机变量可以获得后验分布的采样。对于后验分布的诠释有两种：最大后验(MAP)估计和条件均值(CM)估计。MAP估计指选取最可能的值，即密度函数取值最大的地方，等价于优化问题的求解。CM估计选取后验概率分布的均值，其对应于一个积分问题，实际应用受限于高维积分的庞大计算量，通常通过马尔可夫链蒙特卡罗(MCMC)方法来实现。

在处理高维问题，甚至函数空间时，相应的快速算法与理论分析是研究的热点。文献 [5] 提出了一系列函数空间的MCMC方法，包括预处理Crank-Nicolson (pCN)算法和基于Langevin方程的预处理Crank-Nicolson (pCNL)算法，这两个算法的优势在于结果与问题的离散维数无关，且pCNL算法进一步引入导数信息，加快了Markov链的收敛速度。这些方法更多限定在Gauss先验，而涉及一般非光滑约束的算法讨论不多。对全变差(TV)先验，文献 [6] 指出随着离散化维度的提高TV先验产生的后验分布不具有边缘保持性，不会收敛到一个定义良好的无限维测度。相应地，文献 [4] 提出了以高斯测度作为参考测度并与TV项相混合的TG先验，并构造了分裂pCN算法。这些方法通过定义提议分布和接受率来构造满足细致平衡条件的转移核，引入接受率控制采样来消除渐近误差，相应的Langevin算法被称作MALA算法。其中，接受率一定程度上会影响采样效率。

回顾涉及TV先验的MCMC算法，TV约束并未出现在提案(proposal)中，仅仅在接受率的计算中有所体现 [6] 。而文献 [7] [8] 基于Langevin随机微分方程对一般非光滑凸约束，给出了相应的Langevin系统，并引入Moreau近似获得近似的后验，使得约束部分在提案中有所体现。特别地，基于Langevin随机方程，构造不使用接受率控制采样点的蒙特卡罗方法，称之为ULA算法。文献 [9] 理论分析了ULA算法的收敛性。因为ULA算法不涉及接受-拒绝步，因此在一定的收敛条件下，ULA算法相比MALA算法具有采样效率更高的优点。

本文基于非光滑先验综述现有的采样算法，主要关注ULA算法。特别地，基于凸分析理论，我们将目光聚焦在随机微分方程的构造，提出一种新的ULA算法，期望获得基于非光滑约束快速收敛的Langevin 算法，使其适用于高维问题，并在求解CT成像问题验证方法的优势。

2. 基于非光滑约束的Langevin算法

在实际问题中，如在实际的地震波形反演中，由于地下介质的复杂，常常会遇到解为不连续函数或含尖点的函数，为此为了使重构解具有这些特征，一些非光滑先验被引入。如 $\Omega$ 为 ${ℝ}^d$ 上的有界区域，全变分约束

$R\left(u\right):={\displaystyle {\int }_{\Omega }\left|Du\right|}:=\sup \left\{{\displaystyle {\int }_{\Omega }u\left(divf\right)\text{d}w}:f\in C_0^1\left(\Omega ;{ℝ}^N\right),{\Vert f\Vert }_{L^{\infty }\left(\Omega \right)}\le 1\right\}$ ，

可以很好地反演出跳跃性较大的不连续参数部分。

记 ${\mu }_0=N\left(0,C\right)$ 为X上的Gauss测度，其中C为对称正定的协方差算子。结合非光滑约束 $R\left(u\right)$ 先验，引入混合先验 ${\mu }_{pr}$ ，有

$\frac{\text{d}{\mu }_{pr}}{\text{d}{\mu }_0}\left(u\right)\propto \exp \left(-\alpha R\left(u\right)\right)$ ，

相应的后验分布 ${\mu }_{post}$ 的关于 ${\mu }_0$ 的Randon-Nikodym导数为

$\frac{\text{d}{\mu }_{post}}{\text{d}{\mu }_0}\left(u\right)\propto \exp \left(-\Phi \left(u\right)-\alpha R\left(u\right)\right)$ ，

其中 $\Phi \left(u\right)=\frac{1}{2}{\Vert Au-y\Vert }_{\Sigma }^2=\frac{1}{2}{\Vert {\Sigma }^{-\frac{1}{2}}\left(Au-y\right)\Vert }_2^2$ ， $\alpha >0$ 。

本文主要关心求解高维问题 $Au=y$ ( $A:{ℝ}^N\to {ℝ}^M$ )下基于过阻尼Langevin方程的相关算法。对于目标分布

$\pi \left(u\right)\propto \exp \left(-J\left(u\right)\right)$ ，

若 $J:{ℝ}^N\to ℝ$ 是光滑的，则有相应的Langevin随机微分方程

$\text{d}u=\nabla \log \pi \left(u\right)\text{d}t+\sqrt{2}\text{d}w=-\nabla J\left(u\right)+\sqrt{2}\text{d}w$ ， (1)

其中 $w~N\left(0,I_N\right)$ ， $I_N$ 表示N维单位矩阵，下同。在 ${\displaystyle {\int }_{{ℝ}^N}\exp \left(-J\left(u\right)\right)\text{d}u}<\infty$ 的条件下， $\pi \left(u\right)$ 是关于(1)式的唯一不变分布 [8] ，于是当 $t\to \infty$ ，可对目标分布进行采样。对时间t应用Euler离散，可得马氏链

$u_{k+1}=u_k-\delta \nabla J\left(u_k\right)+\sqrt{2\delta }{w}_{k+1}$ ， (2)

其中 $w_{k+1}~N\left(0,I_N\right)$ ，下同。可以看到(1)式的构造基于J的光滑性，当面临TV等非光滑约束时并不适用。

近端Langevin算法

涉及TV等非光滑约束时，文献 [10] 引入近端算子 $R^{\gamma }$ 来近似函数R

$R^{\gamma }\left(u\right)=\underset{v}{\min }\left\{R\left(v\right)+\frac{1}{2\gamma }{\Vert u-v\Vert }^2\right\}$ ， (3)

其中 $\gamma >0$ 。当 $\gamma \to 0$ 时， $R^{\gamma }$ 点收敛到R，并且 $R^{\gamma }$ 连续可微

$\nabla R^{\gamma }\left(u\right)=\frac{1}{\gamma }\left(u-{\text{prox}}_R^{\gamma }\left(u\right)\right)$ ，

这里

${\text{prox}}_R^{\gamma }\left(u\right)=\underset{v}{\arg \min }\left\{R\left(v\right)+\frac{1}{2\gamma }{\Vert u-v\Vert }^2\right\}$

表示R的近端算子。考虑由混合先验下近似的后验概率密度

${\pi }^{\gamma }\left(u\right)\propto \exp \left(-\Phi \left(u\right)-\frac{1}{2}{\Vert u\Vert }_C^2-\alpha R^{\gamma }\left(u\right)\right)$ ，

其中 ${\Vert u\Vert }_C^2={\Vert C^{-\frac{1}{2}}u\Vert }_2^2$ 。结合对称正定算子K的Langevin随机微分方程 [5]

$\text{d}u=-K\left(C^{-1}u+\nabla \Phi \left(u\right)+\alpha \nabla R^{\gamma }\left(u\right)\right)\text{d}t+\sqrt{2K}\text{d}w$ ，

取 $K=C$ 并对t使用Euler方法离散，设步长为 $\delta$ ，可得马氏链 ${\left(u_k\right)}_{k\ge 0}$

$u_{k+1}=\left(1-\delta \right)u_k-\delta C\left(\nabla \Phi \left(u_k\right)+\alpha \nabla R^{\gamma }\left(u_k\right)\right)+\sqrt{2\delta C}{w}_{k+1}$ 。 (4)

综上，基于Euler离散的近端Langevin (PxEuL)算法具体流程如下：

3. 对偶Langevin算法

这一节，我们基于凸分析理论再次考虑非光滑约束R与Gauss先验的混合约束，构造新的随机微分方程，进而获得新型ULA算法。令约束

$f\left(u\right)=R\left(u\right)+\frac{1}{2\eta }{\Vert u\Vert }_2^2$ ，

注意到R非光滑，因而f是非光滑的。当R为一般凸函数时，f具有强凸性，其Fenchel共轭

$f^{*}\left(\xi \right)=\underset{u}{\sup }\left\{\langle u,\xi \rangle -f\left(u\right)\right\}$

是Frechet可导，且导数 $\nabla f^{*}$ 满足Lipschitz连续。按照凸分析理论可知

$u=\nabla f^{*}\left(\xi \right)\iff u=\underset{u}{\arg \min }\left\{f\left(u\right)-\langle \xi ,u\rangle \right\}$ 。 (5)

实际上，对 $f\left(u\right)=R\left(u\right)+\frac{1}{2\eta }{\Vert u\Vert }_2^2$ ，我们有

$\nabla f^{*}\left(\xi \right)=\underset{u}{\arg \min }\left\{\frac{1}{2\eta }{\Vert u-\eta \xi \Vert }_2^2+R\left(u\right)\right\}$ ，

对比近端近似算子有 $\nabla f^{*}\left(\xi \right)={\text{prox}}_R^{\eta }\left(\eta \xi \right)$ [8] 。近些年，基于非光滑强凸函数成功的结合到迭代正则化方法 [11] [12] ，渐近正则化方法中 [13] [14] ，利用凸分析的理论基础证明了这些方法的收敛性与正则性，数值结果表明TV等非光滑约束成功地刻画了反演解的特征。

受文献 [13] 的启发，我们针对约束问题

$\min \left\{f\left(u\right):Au=y,u\in X\right\}$ ， (6)

定义Lagrangian函数

$L\left(u,\lambda \right)=f\left(u\right)-\langle \lambda ,Au-y\rangle$ ，

及其对偶函数

$V\left(\lambda \right)=f^{*}\left(A^{*}\lambda \right)-\langle \lambda ,y\rangle$ ，

进而关注分布

${\pi }^f\left(\lambda \right)\propto \exp \left(-V\left(\lambda \right)\right)$ 。

假设 $V:{ℝ}^N\to ℝ$ 是连续可微的。考虑 ${\pi }^f\left(\lambda \right)$ 对应的Langevin随机微分方程，取 $K=I$ 有

$\text{d}\lambda =-\nabla V\left(\lambda \right)\text{d}t+\sqrt{2}\text{d}w$ ，

实际上 $V\left(\lambda \right)$ 可导，且 $\nabla V\left(\lambda \right)=A\nabla f^{*}\left(A^{*}\lambda \right)-y$ ，故有

$\text{d}\lambda =-\left(A\nabla f^{*}\left(A^{*}\lambda \right)-y\right)\text{d}t+\sqrt{2}\text{d}w$ 。

我们将Langevin算法与对偶梯度流方法 [13] 相结合，提出了新的随机微分方程

$\{\begin{array}{l}\text{d}\lambda =-\left(Au-y\right)\text{d}t+\sqrt{2}\text{d}w\\ u=\nabla f^{*}\left(A^{*}\lambda \right)\end{array}$ ， (7)

应用Euler离散，设步长为 $\delta$ ，则有马氏链 ${\left({\lambda }_k\right)}_{k\ge 0}$

$\{\begin{array}{l}{\lambda }_{k+1}={\lambda }_k-\delta \left(A{u}_k-y\right)+\sqrt{2\delta }{w}_{k+1}\\ u_{k+1}=\nabla f^{*}\left(A^{*}{\lambda }_{k+1}\right)\end{array}$ 。 (8)

综上，基于非光滑约束的对偶Langevin (DuEuL)算法具体流程如下：

4. CT成像数学模型及其离散

4.1. CT成像问题

CT成像是现代医学一种常见的影像扫描技术，它通过获取人体头颅、心肺、腹部等内部器官的二维断层图像来反映病人的病症，具有密度分辨率高，无创伤等特点，因而被广泛用于临床。传统的CT重建算法是以检测目标为中心，通过X射线旋转扫描，采集目标在不同视角下的投影数据，利用图形重建算法还原出检测目标的断层图像。X射线穿过组织体，射线强度会发生衰退，这一过程可以用Radon变换来描述。记矩形区域 $\Omega \subset {ℝ}^2$ ，相应的非负衰减系数 $u:\Omega \to \left[0,+\infty \right)$ ，当组织体包含在矩形区域中，即 ${\Omega }_1\subset \Omega$ ，当 $x\in \Omega \backslash {\Omega }_1$ 时， $f\left(x\right)=0$ ，有

$A:L^2\left(\Omega \right)\to L^2\left(D\right)$ ，

$\left(Au\right)\left(\theta ,s\right)={\displaystyle {\int }_{L\left(\theta ,s\right)}u\left(l\right)\text{d}l}$ ，

其中 $L\left(\theta ,s\right)=\left\{u\in {ℝ}^2:u_1\cos \theta +u_2\sin \theta =s\right\}$ 为X射线路径， $D=\left\{\left(\theta ,s\right):-r\le s\le r,0\le \theta \le \pi \right\}$ 为投影空间。

在数值模拟中，我们使用在1度到180度之间的30个均匀分布的投影数据，每个投影包含362行光束，所探测的图像离散后为256 × 256。我们借助文献 [15] 的MATLAB包AIRTOOL中函数paralletomo来实现问题的离散，进而获得不适定线性问题 $Au=y$ ，其中A是 $M\times N$ 的稀疏矩阵， $M=10860$ 和 $N=66536$ 。设图像u在两方向上的离散维数分别为n和m，则涉及的非光滑约束TV约束的定义为

${\Vert u\Vert }_{TV}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}\left|{\nabla }_{1}u\right|+\left|{\nabla }_{2}u\right|}}$ ，

其中 $\left({\nabla }_{1}u,{\nabla }_{2}u\right)$ 表示

${\left({\nabla }_{1}u\right)}_{i,j}=\{\begin{array}{l}{u}_{i+1,j}-u_{i,j},i=1,\cdots ,n-1;j=1,\cdots ,m-1\\ u_{n,j+1}-u_{n,j},i=n;j=1,\cdots ,m-1\end{array}$ ；

${\left({\nabla }_{2}u\right)}_{i,j}=\{\begin{array}{l}{u}_{i,j+1}-u_{i,j},i=1,\cdots ,n;j=1,\cdots ,m-1\\ u_{i+1,m}-u_{i,m},i=1,\cdots ,n-1;j=m\end{array}$ 。

4.2. 数值算例

在数值模拟中，真实图像选取为脑部图，如图1所示，对投影数据添加高斯噪声 $y=y^{†}+\epsilon$ ，其中： $\epsilon ~N\left(0,{\sigma }_1^2{I}_N\right)$ ，其中： ${\sigma }_1$ 取测量数据y中最大元素的0.5%。PxEuL算法混合先验中 $C={\sigma }_2^2{I}_N$ 。

在算法的实现过程当中，PxEuL算法涉及求解

${\text{prox}}_R^{\gamma }\left(u\right)=\underset{v}{\arg \min }\left\{R\left(v\right)+\frac{1}{2\gamma }{\Vert u-v\Vert }^2\right\}$

以及DuEuL算法涉及求解

$\nabla f^{*}\left(\xi \right)=\underset{u}{\arg \min }\left\{\frac{1}{2\eta }{\Vert u-\eta \xi \Vert }_2^2+R\left(u\right)\right\}={\text{prox}}_R^{\eta }(\; \eta \; \xi \; )$

的部分，通过主对偶混合梯度方法 [10] [16] 进行有效求解。

我们基于非光滑约束对比贝叶斯推断方法

• PxEuL-TV算法： $\gamma =5$ ， $\delta =1\times {10}^{-4}$ ， $\alpha =1$ ， ${\sigma }_2=0.1$ 。

• DuEuL-TV算法： $\alpha$ 固定为1，分别取不同的 $\eta$ ，并调整步长 $\delta$ 的大小。

其中PxEuL为已有的近端算法，我们只选取了一种参数，而本文的重点为DuEuL算法，实验中共选取了四组参数，需要注意的是，为了使马氏链达到平稳状态，随着 $\eta$ 的变大，相应的步长 $\delta$ 应变小。

为了衡量图像的重构效果，我们使用了相对误差(RelErr)和峰值信噪比(PSNR)等指标，设u是重构得到的解， $u^{*}$ 是真解，则它们的定义如下

$\text{RelErr}=\frac{{\Vert u-u^{*}\Vert }_2}{{\Vert u^{*}\Vert }_2}$ ，

$\text{PSNR}=10{\log }_{10}\frac{{255}^2}{\text{MSE}}\left[\text{dB}\right]$ ，

其中MSE为重构解u的均方误差。除了RelErr和PSNR指标外，我们还使用结构相似性(SSIM)指标来衡量算法结果和原始图像的相似性。

实际算例中，PxEuL和DuEuL算法的初始值 $u_0$ 和 ${\lambda }_0$ 选取为N维零向量，马氏链长为3 × 10⁴，取后1 × 10⁴个点作为平稳后的采样点。贝叶斯方法给出了条件均值(CM)估计和最大后验(MAP)估计，记 $k_0=2\times {10}^4$ 以及 $k_1=3\times {10}^4$ ，数值实验中它们的求解如下

$u_{CM}=\frac{1}{k_1-k_0}{\displaystyle \underset{k=k_0+1}{\overset{k=k_1}{\sum }}{u}_k}$ ，

$u_{MAP}=\underset{k\in \left\{k_0+1,\cdots ,k_1\right\}}{\arg \max }\pi \left(u_k\right)$ ，

Figure 1. Original image

图1. 原始图像

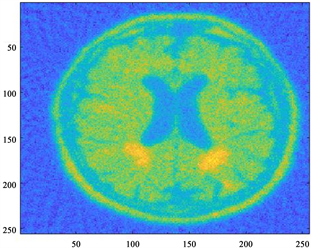
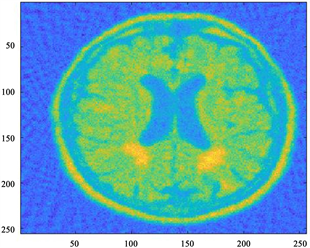(a) (b)

Figure 2. PxEuL algorithm results: MAP estimation (left) and CM estimation (right), $\gamma =5$

图2. PxEuL算法重构结果：MAP估计(左)和CM估计(右)， $\gamma =5$

图2、图3给出了两种算法的重构结果，包括MAP估计和CM估计。从单个算法来看，CM估计比MAP估计更优、更为清晰；从两个算法来看，DuEuL算法给出的重构解相比于PxEuL算法有着更清晰的边界，且背景更颜色更深更接近原始图像。两种算法一定程度上都可以反演出脑部结构，但相比于原始图像，存在背景颜色更浅、反演结果存在伪影的问题。

表1给出了两种算法求解的MAP估计和CM估计对应的相对误差、峰值信噪比和结构相似性等结果。从单个算法来看，CM估计的结果通常优于MAP估计，这说明通过贝叶斯方法给出的CM估计是相当有必要的；从两个算法比较来看，我们提出的DuEuL算法在三个指标上大大优于PxEuL算法，说明DuEuL算法中TV约束更能够刻画反演解的特征。表2给出了DuEuL算法取不同 $\eta$ 时的结果，由MAP估计和CM估计结果可知，随着 $\eta$ 的变大，算法的重构结果更好。

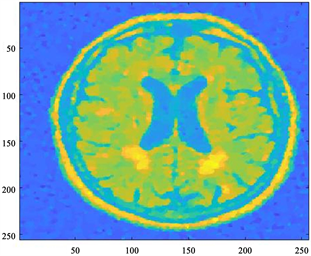
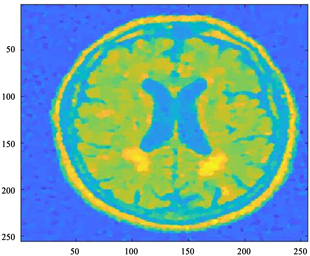(a) (b)

Figure 3. DuEuL algorithm results: MAP estimation (left) and CM estimation (right), $\eta =5$

图3. DuEuL算法结果：MAP估计(左)和CM估计(右)， $\eta =5$

Table 1. Results of two algorithms ( γ = η = 5 )

表1. 两种算法结果( $\gamma =\eta =5$ )

Table 2. DuEuL algorithm results with different parameters taken

表2. 取不同参数DuEuL算法结果

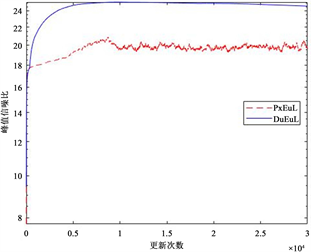
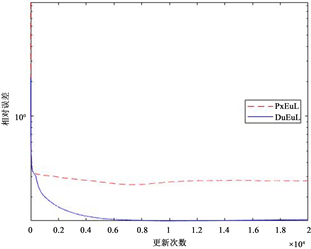
图4给出了两种算法的相对误差和峰值信噪比随着更新次数的变化趋势。从两种算法比较来看，更新初期，PxEuL算法和DuEuL算法变化速度差不多，而后期PxEuL算法存在一定程度的半收敛现象，半收敛现象的程度依赖于参数选取的好坏。另一方面，DuEuL算法最终达到平稳的相对误差值更低，且变化趋势更光滑，没有半收敛现象。

(a) (b)

Figure 4. RelErr and PSNR ratio trend of two algorithms ( $\gamma =\eta =5$ )

图4. 两种算法的相对误差和峰值信噪比趋势( $\gamma =\eta =5$ )

5. 结论

本文基于非光滑约束下的混合先验，提出了对偶Langevin算法，并与近端Langevin算法对比，通过MAP估计和CM估计解相应的指标比较算法的优劣，并基于CT成像问题进行了数值模拟。结果表明DuEuL算法显著优于现有的近端Langevin算法，可以给出更好的重构解，更能够利用TV约束刻画反演解的特征。

基金项目

国家自然科学基金(批准号：12071184)资助项目。

NOTES

^*通讯作者。