基于傅里叶变换的跳跃–扩散模型及欧式期权定价

Fourier Transform-Based Jump-Diffusion Model and European Option Pricing

摘要: 在假设风险资产服从跳跃扩散过程且不产生分红的条件下，基于傅里叶变换和跳跃扩散模型给出了普通欧式看涨期权定价公式，并借助数值分析手段对影响期权价格的因素进行了探讨。结果表明，行权价、到期期限等因素均对期权价格有影响。该方法对于更复杂的期权定价问题同样适用。

Abstract: Under the assumption that the risky asset obeys the jump-diffusion process and does not generate dividends, an ordinary European call option pricing formula is given based on the Fourier transform and the jump-diffusion model, and the factors affecting the option price are explored with the help of numerical analysis. The results show that the exercise price, maturity and other factors have an impact on the option price. This method is also applicable to more complicated option pricing prob-lems.

1. 引言

1973年，Black和Scholes [1] 在标的资产收益率服从正态分布与波动率为常数等假设下，给出了普通欧式期权解析定价公式。然而，BS定价公式的假设条件与真实市场存在较大偏差，为了得到更加符合市场实际的定价模型，诸多学者们进行了广泛的研究。Schmelzele [2] 基于傅里叶变换分析了不同方法中的期权定价。Pellegrino [3] 对单标期权的随机波动率模型予以改进，研究多尺度随机波动率模型。韦铸娥和何家文 [4] 建立随机波动率和跳跃的双因素模型，研究模型参数对复合幂期权定价的影响，分析该模型在期权风险管理上的灵活性。刘朝辉和李翠香 [5] 对跳扩散模型下方法进行改进。曹桂兰和佟昕叶 [6] 在跳–扩散模型下的不同种期权做出了模型研究。孙彩灵和刘丽霞 [7] 在随机利率模型中加入跳跃因素，建立随机利率跳扩散期权定价模型，并将该模型用于远期生效的期权定价。Gómez和Martínez [8] 考虑了双因子利率模型，提出利率遵循跳跃扩散模型。

基于傅里叶变换的期权定价，最早由Heston提出，后被广泛应用。由于其满足风险中性条件，所以与经典BS期权定价公式相比，基于傅里叶变换的期权定价适用于更多期权定价模型，该方法对于不同期权定价模型，给出了一般性公式，由于每个模型的特征函数不同，由傅里叶变换推导出的模型定价公式也不同。Merton [9] 基于标的资产服从跳跃扩散过程的假设提出了跳跃扩散模型，该模型在标的资产价格的变化过程中引入了Poisson的跳跃扩散因子，这种因子能够很好地描述实际市场中资产价格受到某些突发事件的冲击所产生的跳跃情况，从而更加反映资产价格的实际波动情况，因此，本文针对标的资产价格存在跳跃的情况，在基于傅里叶变换的跳跃扩散模型基础上，分析影响期权价格的因素。

2. 模型与记号

假设带流概率空间为 $\left(\Omega ,F,Q,{\left(F_t\right)}_{0<t\le T}\right)$ ，金融市场是无风险套利的，并且存在可供选择的债券资产 $B_t$ 、风险资产 $S_t$ ，债券资产满足如下方程： $\text{d}{B}_t=r\ast B_t\text{d}t$ ，其中债券价值 $B_t={\text{e}}^{-\left(T-t\right)r}$ ， $S_t$ 是具有跳跃和扩散特征的不分红的风险资产。

Merton跳跃扩散模型假设在某一固定时间t时，风险资产 $S_t$ 具有如下随机方程 [10] ：

$\text{d}{S}_t=\left(r-r_j\right)S_t\text{d}t+\sigma S_t\text{d}{Z}_t+J_t{S}_t\text{d}{N}_t$

其中，r为市场的无风险利率， $r_j$ 为跳跃过程的漂移项，且 $r_j=\lambda \left({\text{e}}^{{\mu }_J+\frac{{\delta }^2}{2}}-1\right)$ ，

$\delta$ 为跳跃的波动率， ${\mu }_J$ 为跳跃幅度的均值， $\sigma$ 为风险资产的价格波动率， $Z_t$ 为标准布朗运动， $N_t$ 是强度为 $\lambda$ 的泊松过程， $J_t$ 为风险资产价格发生跳跃时的跳跃高度，且 $\ln \left(1+J_t\right)~N\left(\ln \left(1+{\mu }_J\right)-\frac{{\delta }^2}{2},{\delta }^2\right)$ 。

3. 跳跃–扩散模型

定义1：假设随机变量X的风险中性概率密度函数为 $q\left(x\right)$ ，那么X的特征函数 $\hat{q}$ 就是其概率密度函数的傅里叶变换：

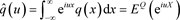
考虑一个执行价格为K的欧式期权，其T时刻的价格为 $C_T$ ，那么有 $C_T=\max \left\{\omega \left(S_T-K,0\right)\right\}$ ， $\omega \in \left\{-1,1\right\}$ 。 $\omega =-1$ 对应看跌期权， $\omega =1$ 对应看涨期权。当 $t=0$ 时：

$C_0={\text{e}}^{-rT}{\displaystyle {\int }_0^{\infty }{C}_T\left(z\right)q\left(z\right)\text{d}z}$

其中， $q\left(z\right)$ 为风险资产 $S_t$ 的风险中性概率密度函数。

利用傅里叶变换对期权定价公式进行求解。令 $x=\ln S_T$ ，则欧式看涨期权的到期收益为 $C_T=\max \left({\text{e}}^x-K,0\right)$ 。对于 $z=u+iv$ ，且 $v>1$ ， $C_T$ 的傅里叶变换如下所示：

${\hat{C}}_T\left(z\right)={\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-izx}\max \left({\text{e}}^x-K,0\right)\text{d}x}=-\frac{K^{1-iz}}{z^2+zi}$

根据傅里叶逆变换可得：

$C_T\left(x\right)=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty +iv}^{\infty +iv}{\text{e}}^{izx}{\hat{C}}_T\left(z\right)\text{d}z}$

那么，根据无风险收益率对T时刻的期望收益进行折现可得 $t=0$ 时刻的期权估值：

$C_0\left(z\right)={\text{e}}^{-rT}{E}_0^Q\left(C_T\left(x\right)\right)=\frac{{\text{e}}^{-rT}}{2\pi }{\displaystyle {\int }_{-\infty +iv}^{\infty +iv}{\hat{C}}_T\left(z\right)\hat{q}\left(z\right)\text{d}z}$

假设 $S_t=S_0{\text{e}}^{rT+X_t}$ ，且 $X_t$ 服从Lévy过程，同时假设 ${\text{e}}^{X_t}$ 为一个鞅且 $X_0=0$ ，有 $\hat{q}\left(z\right)={\text{e}}^{izy}\phi \left(z\right)$ ，其中 $\phi$ 是 $X_t$ 的特征函数，式中 $y=\ln S_0+rT$ ，于是有：

$C_0\left(x\right)=\frac{{\text{e}}^{-rT}}{2\pi }{\displaystyle {\int }_{-\infty +iv}^{\infty +iv}{\text{e}}^{izy}{\hat{C}}_T\left(z\right)\phi \left(z\right)\text{d}z}$

令 $k=\ln \left(\frac{S_0}{K}\right)+rT$

$C_0\left(x\right)=\frac{K{\text{e}}^{-rT}}{2\pi }{\displaystyle {\int }_{-\infty +iv}^{\infty +iv}{\text{e}}^{izk}\phi \left(z\right)\frac{\text{d}z}{z^2+zi}}$

上式具有两个奇异点 $z=-i$ 与 $z=0$ ，根据 ${\text{e}}^k=\frac{S_0}{K}{\text{e}}^{rT}$ 、 $\phi \left(-i\right)=1$ 、 $i^{-1}=-i$ ，进行残数计算可得：

$\text{Res}\left(-i\right)=\frac{K{\text{e}}^{-rT}}{2\pi }{\text{e}}^{k\frac{\phi \left(-i\right)}{i}}=\frac{S_{0}i}{2\pi }$

根据残数定理可以得到看涨期权价格为对v的积分减去 $2\pi i\text{Res}\left(-i\right)$ ，得到

$C_0=S_0-\frac{K{\text{e}}^{-rT}}{2\pi }{\displaystyle {\int }_{-\infty +iv}^{\infty +iv}{\text{e}}^{-izk}\phi \left(z\right)\frac{\text{d}z}{z^2+zi}}$

设v = 0.5，可得

$C_0=S_0-\frac{K{\text{e}}^{-rT}}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-i\left(z+i/2\right)k}\phi \left(z+i/2\right)\frac{\text{d}z}{{\left(z+i/2\right)}^2+\left(z+i/2\right)i}}$

${\text{e}}^{-iz\left(+i/2\right)k}={\text{e}}^{-izk}{\text{e}}^{k/2}$ ， $K{\text{e}}^{-rT}{\text{e}}^{k/2}={\text{e}}^{-rT/2}\sqrt{S_{0}K}$ 。

令 $z=u+i$ ，有：

$C_0=S_0-\frac{{\text{e}}^{-rT/2}\sqrt{S_{0}K}}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-iuk}\phi \left(u+3i/2\right)}\frac{\text{d}u}{u^2+2ui-3/4}$

对于可积且实值的f，通过傅里叶变换和特征函数在z = 0附近的对称性，可得 [11] ：

$f\left(x\right)=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-izx}\hat{f}\left(z\right)\text{d}z}=\frac{1}{\pi }\mathrm{Re}\left[{\displaystyle {\int }_0^{\infty }{\text{e}}^{-izx}\hat{f}\left(z\right)\text{d}z}\right]$

从而可得 [12] ：

$C_0=S_0-\frac{{\text{e}}^{-rT/2}\sqrt{S_{0}K}}{\pi }{\displaystyle {\int }_0^{\infty }\mathrm{Re}}\left[{\text{e}}^{-iuk}\phi \left(u+3i/2,T\right)\right]\frac{\text{d}u}{u^2-3/4}$

其中， $\mathrm{Re}\left[x\right]$ 为实部， $\phi$ 为Merton跳跃扩散模型中期权标的资产所对应的特征函数，w为风险中性漂移项：

$\phi =\exp \left(\left(iuw-\frac{u^2{\sigma }^2}{2}+\lambda \left({\text{e}}^{iu{\mu }_J-u^2{\delta }^2/2}-1\right)\right)T\right)$

$w=r-\frac{{\sigma }^2}{2}-\lambda \left({\text{e}}^{{\mu }_J+{\delta }^2/2}-1\right)$

同理可得，欧式看跌期权的现值和特征函数之间的公式为：

$C_0=S_0-\frac{{\text{e}}^{-rT/2}\sqrt{S_{0}K}}{\pi }{\displaystyle {\int }_0^{\infty }\mathrm{Re}}\left[{\text{e}}^{-iuk}\phi \left(u+3i/2,T\right)\right]\frac{\text{d}u}{u^2-3/4}$

4. 数值分析

上式可以通过数值积分法进行求解。本文假设的初始参数如下： $S_0=100$ ， $r=0.05$ ， $K=100$ ， $T=1$ ， $\lambda =0.75$ ， $\delta =0.1$ ， ${\mu }_J=-0.2$ ， $\sigma =0.4$ 。其中，S₀为标的资产在0时刻的价格，K为欧式期权的执行价格。

1) 期权价格与标的资产的比较

图1横坐标为标的资产价格，纵坐标为期权价格。Merton_Call_value为Merton跳跃扩散看涨期权价格，Inner_value为欧式期权到期时的价格。当标的资产价格低于期权行权价时，期权价格较低，当标的资产价格高于期权行权价时，期权价格较高，并且期权价格高于其到期时的价格。

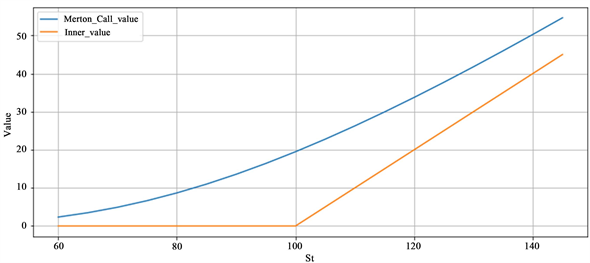
Figure 1. Comparison of option prices with the underlying asset

图1. 期权价格与标的资产比较

2) 期权价格与行权价的比较

图2横坐标为看涨期权行权价，纵坐标为期权价格。将标的资产价格设为100。当风险资产价格大于行权价时，期权价格较高，当风险资产价格小于行权价时，期权价格较低。

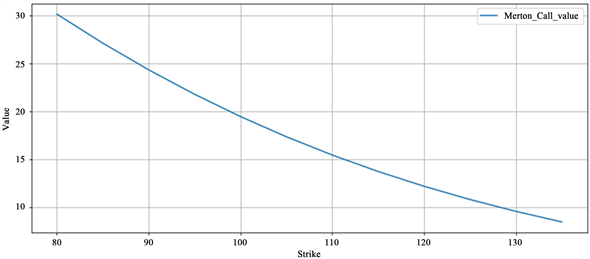
Figure 2. Comparison of option prices and strike prices

图2. 期权价格与行权价比较

3) 期权价格与到期期限的比较

图3横坐标为看涨期权到期期限，纵坐标为期权价格。当期权到期期限较小时，期权价格较低，期权到期期限较大时，期权价格较高。

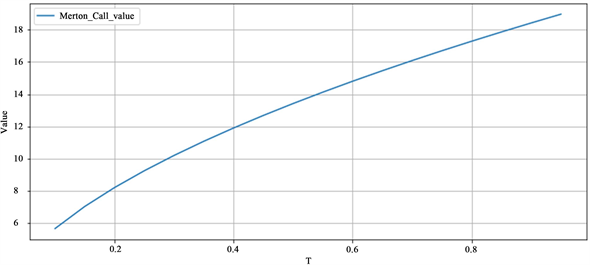
Figure 3. Comparison of option prices and maturity periods

图3. 期权价格与到期期限比较

4) 期权价格与跳跃波动率 $\delta$ 的比较

图4横坐标为跳跃波动率 $\delta$ ，纵坐标为期权价格。当跳跃波动率较小时，期权价格较低，跳跃波动率较大时，期权价格较高。

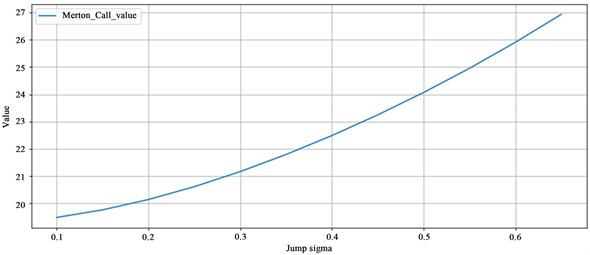
Figure 4. Comparison of option price and jump volatility $\delta$

图4. 期权价格与跳跃波动率 $\delta$ 比较

5) 期权价格与标的资产波动率 $\sigma$ 的比较

图5横坐标为标的资产波动率 $\sigma$ ，纵坐标为期权价格。当标的资产波动率较小时，期权价格较低，标的资产波动率较大时，期权价格较高。

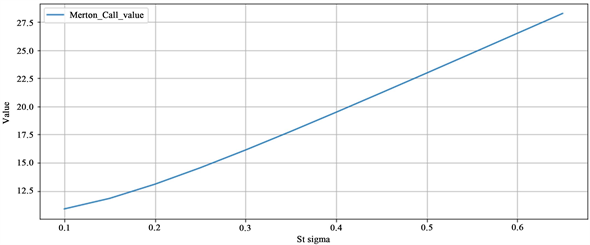
Figure 5. Comparison of option price and underlying asset volatility $\sigma$

图5. 期权价格与标的资产波动率 $\sigma$ 比较

5. 结论

本文基于傅里叶变换的跳跃–扩散模型推导出欧式期权定价公式，同时进行数值分析，研究了期权价格的影响因素。对欧式期权而言，标的资产价格越高期权价格越高、行权价越高期权价格越低、到期期限越小期权价格越低、跳跃波动率与标的资产波动率越高期权价格越高。本文提出的方法还可以应用到任选期权、障碍期权、亚式期权等复杂期权的定价问题。